Степени свободы системы дифференциальных уравнений
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ДИНАМИКЕ
Исследование колебаний механической системы с одной степенью свободы
Эти задачи следующие:
2. Построение расчетной схемы .
Ф ормулировка задачи — это условие ( текст) з адачи. Она осу ществляется руководител ем работ сов местно с испол нителе м.
Рас четная схема — эт о рисунок , на ко тор ом изображены :
а) ра циональ но выбранная система координат;
Математическая моде ль — э то система д иф фере нциальных уравн ений, алгебраических уравнений и на чальн ых условий, описывающих динамическое поведение механической системы.
Дано: m1, m2, m3 — массы тел механической системы, с — жесткость упру гого элемента, r 1 — радиус одн ородн ого катка 1, r2, R2 — радиусы ст упеней блока 2, i2 — рад иус инерции блока 2 , 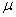
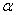
Определить: применяя основные теоремы динамики системы и аналитические методы теоретической механики, определить закон движения первого тела и реакции внешних и внутренних связей. Провести численный анализ полученного решения с использованием ЭВМ.
Порядок выполнения работы:
3) Сформулировать начальные услови я движения.
4) Найти решение дифференциального уравнения движения.
6) По дставив на йденные постоянны е интегрирования в решение дифференциального уравнения, записать закон движ ен ия объ ект а .
8) Построить алгоритм вычис лени й для реализации н а ЭВМ.
9) Произ вес ти вычисления в дисплейном классе.
10) Произв ес ти графическую обработк у результатов вычис лений.
1. Применение основных теорем динамики механической системы
1.1. Постановка второй основной задачи динамики механической системы
Расчетная схема представлена на рис.2
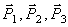
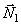
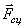
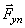
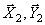
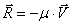
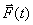
Рассматриваемая механическая система имеет одну степень свободы (нити нерастяжимые, качение катка 1 происходит без скольжения). Будем определять ее положение с помощью координаты S. Начало отсчета координаты совместим с положением статического равновесия центра масс груза 3.
Для пост роения дифферен циального уравнения движен ия с истемы используем теорему об изменении к инетической энергии механической системы в форме:
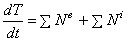
где Т — кинетическая энергия системы,
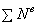
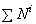
Теорема (1.1) формулируется так: «Производная по времени от кинетической энергии механической системы равн а алгебраической сумме мощностей внеш них и внутренних сил, д ейс твующих на точки механической системы».
Вычислим ки нетическую энергию сис темы как сумму кинетических эн ергий тел 1-3:
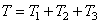
Каток 1 совершает плоскопараллельное движение, поэто му его кинетическая энергия опре деляется по теореме Кенига:
где VC1 – скорость центра масс катка;
JC1 – момент инерции относительно центральной оси катка;
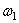
Блок 2 совершает вращ ательное движение около неподвижной оси. Его кинетическая энергия
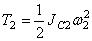
где JC2 – момент инерции относительно центральной оси блока;
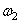
Груз 3 совершает поступательное движение. Его кинетическая энергия равна:
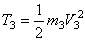
Кинетическая энергия всего механизма будет равна:
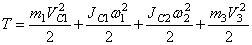
Выразим VC1, 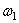
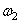
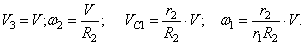
Подставляя (1.3), (1.4), (1.5) в (1.6) с учетом (1.7), получаем:
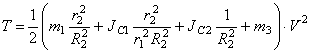
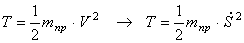
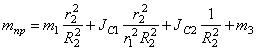
Величину 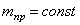
Найдем производную от кинетической энергии по времени
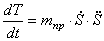
Теперь вычислим правую часть уравнения (1.1) — сумму мощностей внешних и внутренних сил.
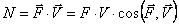
Рассматриваемая нами механическая система является неизменяемой, т.е. тела, входящие в систему, недеформируемы и скорости их точек относительно друг друга равны нулю. Поэтому сумма мощностей всех внутренних сил будет равняться нулю:
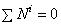
Будут равняться нулю и мощности некоторых внешних сил, приложенных в точках, скорости которых равны нулю. Как видно из расчетной схемы, таковыми являются силы
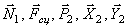
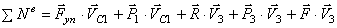
или, раскрывая скалярные произведения,
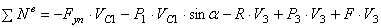
С учетом кинематических соотношений (1.7) сумму мощностей внешних сил преобразуем к виду:
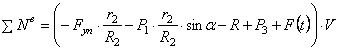
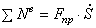
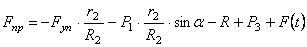
Величину F пр будем называть приведенной силой.
Преобразуем выражение (1.18). Упругую силу считаем пропорциональной удлинению пружины. Полное удлинение пружины f равно сумме статического f ст и динамического SC1 удлинений
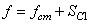
причем из выражения (1.7) для VС1 следует, что 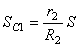
Тогда упругая сила будет равна:
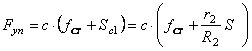
Сила вязкого сопротивления 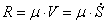
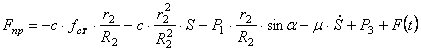
В состоянии покоя приведенная сила равна нулю. Полагая в (1.20) 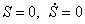
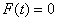
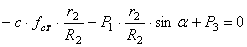
Из уравнения (1.21) определяется статическое удлинение пружины
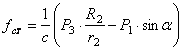
Учитывая (1.22) в (1.20), получаем окончательное выражение для приведенной силы:
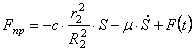
Подставим выражения для производной от кинетической энергии (1.11) и сумму мощностей всех сил (1.17) с учетом (1.23) в уравнение (1.1). Тогда, получаем дифференциальное уравнение движения системы:
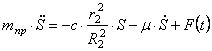
Запишем последнее уравнение в виде:
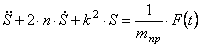
где введены коэффициенты, имеющие определенный физический смысл:
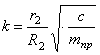
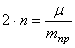
Запишем начальные условия движения:
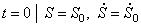
В ыражения (1.25) и (1.26) совместно представляют математическую модель для решения второй задачи динамики.
1.2. Определение закона движения системы.
Проинтегрируем дифференциальное уравнение (1.25). Пусть возмущающая сила изменяется по гармоническому закону:
где 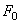
р — циклическая частота возмущения.
Общее решение S неоднородного дифференциального уравнения (1.25) складывается из общего решения однородного уравнения 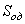
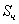
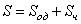
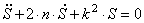
Решение этого уравнения ищем в виде функции
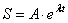
где А и 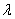
Подставляя (2.3) в (2.2), получаем:
Так как мы ищем нетривиальное решение, то 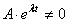
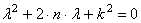
Уравнение (2.4) называется характеристическим уравнением дифференциального уравнения (2.2). Это уравнение имеет два корня:
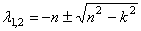
В зависимости от знака подкоренного выражения, корни характеристического уравнения могут быть комплексно-сопряженными или действительными. Возможны три случая:
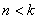
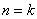
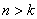
В первом случае ( 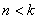
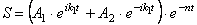
где А 1 , А2 – постоянные интегрирования,
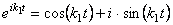
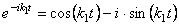
нетрудно представить в виде:
где a , 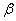
Во втором случае ( 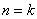
В третьем случае ( 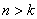
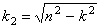
Далее предполагается, что в рассматриваемом примере имеет место случай 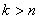
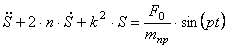
Частное решение ищем в виде правой части
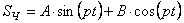
Сравнивая коэффициенты при соответствующих тригонометрических функциях справа и слева, получаем систему алгебраических уравнений для определения постоянных А и В:
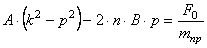
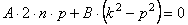
Решая эту систему, получаем следующие выражения для коэффициентов А и В:
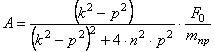
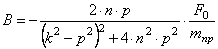
Таким образом, решение (2.12) определено. Складывая (2.8) и (2.12), получаем общее решение неоднородного уравнения (2.11)
Константы а и 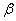
Подчинив (2.14) и (2.15) начальным условиям, получим систему уравнений относительно искомых констант
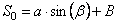
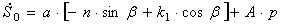
Решая эту систему, получаем:
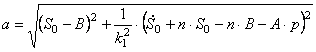
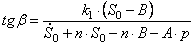
Подставляя (2.16) в (2.14), получаем закон движения механизма.
1.3. Определение реакций внешних и внутренних связей.
Для решения этой задачи расчленяем механизм на отдельные части и изображаем расчетные схемы отдельно для каждого тела (рис.3).
Определение реакций связей проведем с помощью теоремы об изменении количества движения
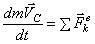
и теоремы об изменении кинетического момента относительно центра масс
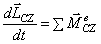
В соответствии с расчетными схемами (рис. 3) записываем уравнения (3.1) и (З.2) в проекциях на оси координат
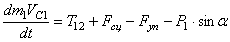
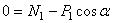
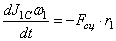
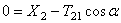
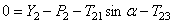
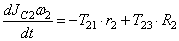
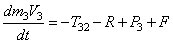
С учетом кинематических соотношений (1.7) систему уравнений (3.3) -(3.9) преобразуем к виду:
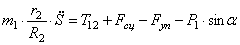
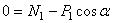
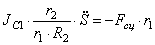
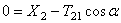
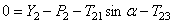
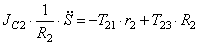
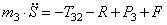
Уравнения (3.10) составляют систему алгебраических уравнений относительно функций
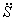
Решая эту систему, получаем и дифференциальное уравнение движения системы, и выражения для определения реакций.
2.1. Составлени е дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа.
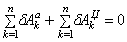
Здесь 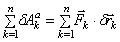
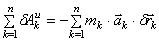
Изобразим на рисунке активные силы и силы инерции (рис.4). Реакции идеальных связей 
Сообщим системе возможное перемещение. Возможная работа активных сил определяется как сумма следующих элементарных работ:
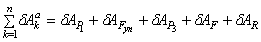
Вычисляя последовательно элементарные работы активных сил и суммируя их, получаем после несложных преобразований
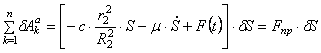
Аналогичное выражение для приведенной силы F пр получено ранее [см. (1.23)].
Найдем возможную работу сил инерции:
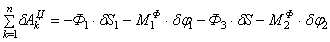
Для величин главных векторов и главных моментов сил инерции имеем следующие выражения:
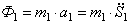
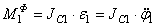
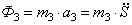
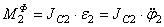
Используя кинематические соотношения (1.7), можно записать
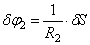
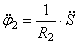
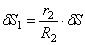
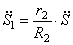
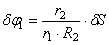
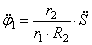
Тогда возможную работу сил инерции можно преобразовать к виду
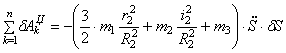
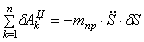
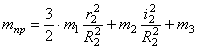
Аналогичное выражение для приведенной массы системы было получено ранее [см.(1.10)]. Подставляя выражения (4.3) и (4.8) в общее уравнение динамики (4.1), получаем
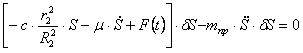
Поделив (4.10) на 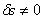
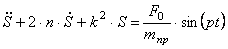
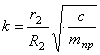
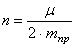
Дифференциальное уравнение (4.11) полностью совпадает с полученным ранее уравнением (1.25).
2.2. Составление дифференциального уравнения движения механизма с помощью уравнений Лагранжа 2— го рода.
Составим теперь уравнения Лагранжа 2-го рода. Для механической системы с одной степенью свободы дифференциальное уравнение движения в обобщенных координатах имеет вид:
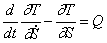
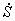
Выражение для кинетической энергии системы было найдено ранее (1.8):
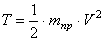
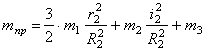
Учитывая, что 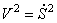
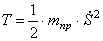
Производные от кинетической энергии
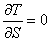
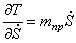
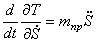
Для определения обобщенной силы Q сообщим системе возможное перемещение 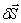
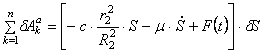
С другой стороны для системы с одной степенью свободы
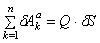
Сравнивая два последних соотношения, получаем
Подставляя производные от кинетической энергии (4.15) и обобщенную силу (4.16) в уравнение Лагранжа, получаем
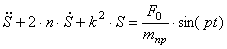
Полученное уравнение (4.18) совпадает с уравнениями (1.25) и (4.11).
3. Анализ колебаний механической системы с одной степенью свободы
3.1. Колебания механической системы при отсутствии сил сопротивления среды
В дифференциальном уравнении движения системы, полученном ранее (1.25), полагаем 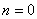
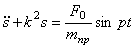
Начальные условия: при 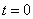
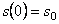
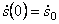
3.1.1. Свободные колебания
Если внешнее возмущение отсутствует (т.е. 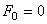
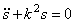
и называется дифференциальным уравнением свободных колебаний, т.е. таких движений системы, которые происходят под действием так называемых восстанавливающих сил. Восстанавливающие силы – это такие силы, каждая из которых стремится вернуть систему в состояние статического равновесия (силы тяжести, упругие силы).
Решение уравнения (5.2) с учетом начальных условий имеет вид:
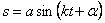
где 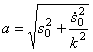
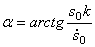
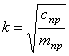
Анализируя решение (5.3) можно сделать следующие выводы:
1. Свободные колебания (рис.5.1) системы с одной степенью свободы представляют собой гармонические колебания.
2. Амплитуда 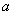
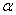
3. Циклическая частота 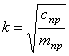
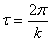
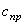
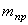
4. Отношения амплитуд колебаний различных точек системы не зависят от начальных условий, так как начальные условия влияют на амплитуды только через множитель 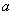
5. Все точки системы всегда находятся в одной фазе, т.е. они одновременно проходят через свои равновесные положения; координаты всех точек одновременно достигают своих максимальных значений.
3.1.2. Вынужденные колебания
При воздействии возмущающей силы 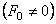
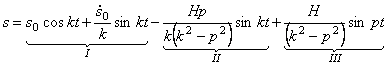
где 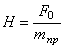
Первые два слагаемых правой части уравнения (5.5):
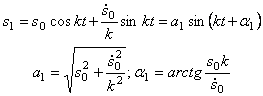
соответствуют свободным колебаниям с частотой 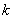
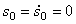
Третье слагаемое в (5.5)
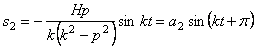
— гармоническое колебание, происходящее с собственной частотой 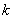
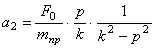
Эти колебания также относятся к свободным колебаниям. Они всегда сопровождают вынужденные колебания при любых начальных условиях, от которых они вообще не зависят.
Их называют сопровождающими колебаниями (рис. 5.2).
Четвертое слагаемое в выражении (4.5):
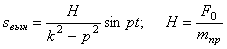
представляет собой вынужденные колебания системы (рис. 5.3).
Таким образом, колебания линейного осциллятора в рассмотренном случае представляют собой линейное наложение трех гармонических колебаний: свободных, сопровождающих и вынужденных (рис. 5.4).
Отметим следующие свойства вынужденных колебаний:
1. Вынужденные колебания происходят с частотой возмущающей силы.
2. Вынужденные колебания не зависят от начальных условий, поэтому для изменения, например, амплитуды (при заданной возмущающей силе) вынужденных колебаний необходимы существенные изменения параметров конструкции: ее жесткости, распределения масс, тогда как в свободных колебаниях для этого достаточно изменить начальные условия.
3. Если 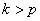
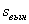
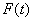
Если 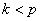
Переписав для этого случая выражение (5.9) в виде:
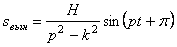
убеждаемся, что при 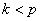
4. Если 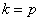
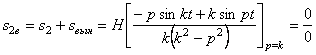
т.е. получим неопределенность, которую можно раскрыть по правилу Лопиталя , заменив дробь в (5.11) пределом
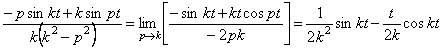
Таким образом, в этом случае общий интеграл (5.5) будет иметь вид:
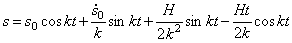
И здесь, как в (5.5) движение осциллятора представляет собой линейное наложение трех колебательных движений, но с одним существенным отличием от (5.5): вынужденные колебания представлены непериодическим слагаемым:
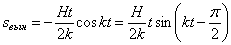
в коэффициенты которого входит время t .
С течением времени он растет по абсолютной величине безгранично, причем вынужденные колебания происходят с возрастающей по линейному закону амплитудой.
Такая ситуация при колебаниях называется резонансом.
5. Если частота вынужденных колебаний не равна частоте свободных колебаний, но близка к ней, то, записав выражение (5.11) в виде:
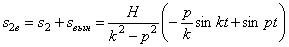
полагаем 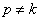
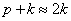
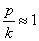
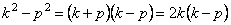
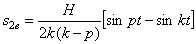
Используя тригонометрическое выражение:
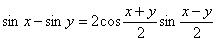

т.е. 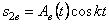
где 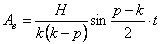
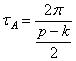
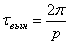
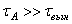
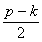
Подобная рассмотренному случаю ситуация представляет собой биение (рис. 5.5).
Таким образом, когда частота вынужденных колебаний весьма близка к частоте свободных (или собственных) колебаний системы, но не равна ей, в колебательной системе возникает биение.
3.2. Колебания механической системы в вязкой среде
Дифференциальное уравнение движения имеет вид (1.25):
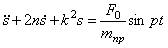
Начальные условия: 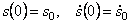
3.2.1. Свободные колебания
Полагая в (5.17) 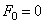
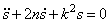
Ограничимся случаем малых сопротивлений и примем 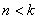
Тогда общее решение однородного уравнения (5.19) с учетом начальных условий можно представить в виде (рис. 5.6):
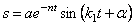
где 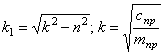
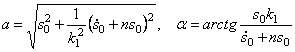
Из закона движения системы (5.20) видно, что в сопротивляющейся среде:
1) свободные колебания являются затухающими;
2) частота затухающих колебаний 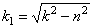
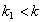
3) амплитуда затухающих колебаний 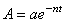
4) период затухающих колебаний 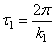
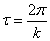
5) отношение любых двух соседних амплитуд: 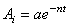
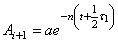
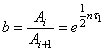
Это отношение называется декрементом затухания. Логарифм этого коэффициента
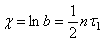
называется логарифмическим декрементом.
Декремент или логарифмический декремент используются для оценки быстроты убывания амплитуды затухающих колебаний.
3.2.2. Вынужденные колебания в сопротивляющейся среде
Дифференциальное уравнение движения в этом случае является неоднородным:
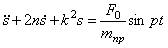
его общее решение имеет вид:
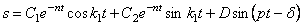
При начальных условиях 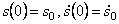
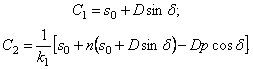
После подстановки постоянных интегрирования (5.27) в общее решение (5.26) получим закон движения механической системы:
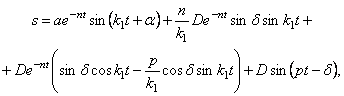
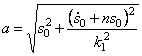
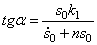
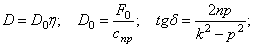
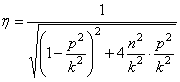
В выражении (5.28) первое слагаемое представляет собой собственные затухающие колебания (рис. 5.6):
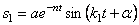
Второе и третье слагаемые в совокупности представляют собой сопровождающие колебания (рис. 5.7):
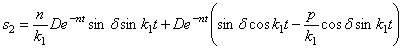
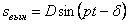
— вынужденные колебания с частотой возмущающей силы (рис. 5.8).
Таким образом, амплитуда вынужденных колебаний при резонансе достигает значительной величины при малых сопротивлениях.
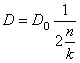
Если 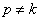
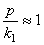
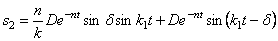
Рассматривая (5.33) и (5.35) совместно и, добавив выражение
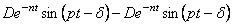
равное нулю, получим закон движения механической системы в виде:
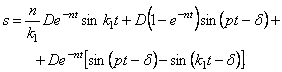
Но выражение в квадратных скобках можно представить так (5.15):
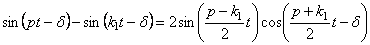
Тогда получим, положив 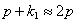

Последнее слагаемое в (5.38) представляет собой колебания биений с затухающей амплитудой
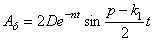
т.е. 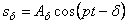
Второе слагаемое в (5.38) – это незатухающие вынужденные колебания
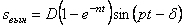
Первое слагаемое в (5.38) – это затухающие сопровождающие колебания
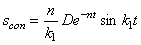
Таким образом, в реальных условиях 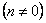
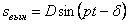
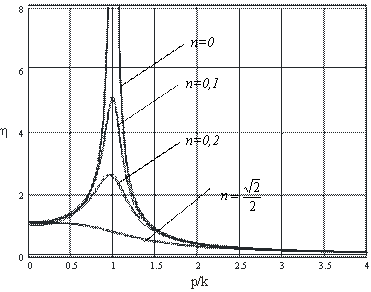
3.3. Коэффициент динамичности
Как было отмечено выше (5.31), коэффициентом динамичности называется отношение максимального динамического отклонения механической системы от положения устойчивого равновесия к статическому отклонению под воздействием силы, равной амплитуде возмущающей силы (рис. 5.10).
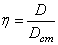
где 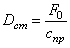
т.е. согласно выражению (5.31):

Максимальное значение 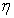
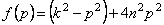
Найдем, при каком значении р функция (5.44) минимальная.
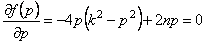
Из (5.45) следует, что
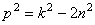
Это возможно, если
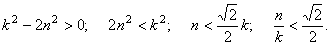
Подставляя (5.46) в (5.43), получаем

При малом значении сопротивления 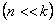
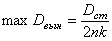
При резонансе 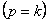
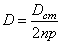
т.е. максимальное значение амплитуды и ее значение при резонансе весьма близки друг к другу (практически одинаковы).
В области, достаточно удаленной от резонанса, при установившемся движении и малом коэффициенте затухания, силами сопротивления можно пренебрегать.
Графические иллюстрации видов колебаний
Рис. 5.1. Собственные колебания
Рис.5.2 Сопровождающие колебания
Рис.5.3 Вынужденные колебания
Рис. 5.4 Результирующие колебания
Рис. 5.5 Биения – результирующие колебания
Колебания в вязкой среде
Рис.5.6. Собственные колебания в вязкой среде
Рис.5.7 Сопровождающие колебания в вязкой среде
Рис. 5.8. Вынужденные колебания
Рис. 5.9 Результирующие колебания в вязкой среде
Рис. 5.10 Коэффициент динамичности
Рис. 5.11. Резонанс ( 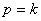
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Свободные колебания системы и степени свободы
















Свободные колебания системы с одной степенью свободы
- Система 6es свободно отбрасывает с усилием сопротивления. Механическая система называется системой 1 степени свободы, если ее положение в пространстве уникально. Она определяется присвоением одной величины q, называемой общими координатами. Движение системы в пространстве описывается временной зависимостью обобщенных координат. Возьми это. Рассмотрим положение начала координат обобщенной системы и устойчивое равновесие нулевого уровня потенциальной энергии, малое движение системы вокруг этого положения равновесия. Отклонение системы от положения равновесия при выборе такой опорной точки определяется величиной обобщенных координат.
Предположим, что составлено небольшое дифференциальное уравнение В случае движения по общим координатам и малой величины общей скорости, которая отсчитывается от положения равновесия, она ограничивается линейным членом дифференциального уравнения движения. Этот. Метод отбрасывания в терминах нелинейных дифференциальных уравнений, включающий квадратные и более продвинутые обобщенные координаты и скорости Линеаризация уравнения. Конечно, такая линеаризация в некоторой степени искажает действительный образ движения, но тем меньше отклонение системы от устойчивого положения Если она находится в равновесии, то линеаризованное уравнение движения системы описывается более точно.
Кольцо совершает сложное движение, которое можно разложить па относительное по отношению к проволоке и переносное вращательное вместе с проволокой вокруг вертикальной оси х. Людмила Фирмаль
Линеаризация дифференциальных уравнений позволяет получить замкнутые решения таких систем. Как правило, невозможно найти точный Интеграл системы нелинейных уравнений в ее окончательном виде. Удобный способ создания дифференциального уравнения малой вибрации В системе используется уравнение Лагранжа. Эти уравнения системы с 1 степенью свободы, где t-кинетическая энергия системы, обобщаются координаты q и обобщенная скорость q-обобщенная сила.
Кинетическая энергия системы, на которую воздействуют стационарные связи, выражается формулой t-j в терминах обобщенных координат и скоростей. Л 2, где q-положительная функция обобщенных координат q. Затем, чтобы линеаризовать выражение кинетической энергии, ряд Маклорина Л-Л0ЛО7ЦИв,.
Разверните вопрос .Это значение уравнения 2 равно Г1Л0 4л0 4 .4 .Затем, предполагая, что dn мал, для краткости он приближается к S, где константа A 0 обозначается a .эта константа всегда Положительный .Это называется коэффициентом инерции .Для линейных обобщенных координат коэффициент инерции a имеет размерность массы, а для угловых координат-размерность момента Инерции твердого тела .Потенциальная энергия системы является функцией обобщенной координаты ПП9 .6 разверните эту функцию в макросерии вблизи положения устойчивого равновесия п-п .0 p-0, 1p-0, h-и h .. 7 в этом уравнении p 0 0, 8.
Это происходит потому, что положение равновесия выбирается относительно нулевого уровня потенциальной энергии. Обобщенная сила положения равновесия Итак, поскольку он равен нулю, строка 7 начинается с пункта 3. Отбрасывание членов более высокого порядка и указание краткости p 0 дает p us, 10. Где константа находится c называется квазиупругим модулем упругости. В случае устойчивого равновесия с 0.
Введение кинетической энергии 5 и потенциала 10 в уравнение Лагранжа 1 Дифференциальное уравнение для малых свободных колебаний системы со степенью свободы от 0 до 1. 11. Это уравнение имеет структуру, аналогичную свободному дифференциальному уравнению. Изменение массы, возникающее под действием линейной восстанавливающей силы. Общая форма интеграла в уравнении 11 дана для простоты. Где l-амплитуда Колебаний, a-начальная фаза, т а-фаза колебаний, а-круговая частота вибрации, часто называют просто частотой вибрации. Определены амплитуда и начальная фаза колебаний В соответствии с начальными условиями.
Если обобщенные координаты в t q и начальные значения их производных равны 0, о, то период колебаний-t-2 k-14 свободен, или иначе получается соответствующее значение. Вибрация системы, определяемая уравнением 12, является гармонической вибрацией. Их частота и период не зависят от исходных данных-эта характеристика называется малой изохронностью Колебания. Заметим, конечно, что дифференциальное уравнение свободной вибрации 11 может быть описано без применения уравнения Лагранжа. Когда решить проблему бесплатно 1 вибрация системы dof, следующие шаги порекомендованы.
Первый способ-применение уравнения Лагранжа 1 и выбор обобщенных координат q 2 В системе выражений кинетической энергии g3 можно найти только потенциальную энергию p или вычислить значение обобщенной 4 путем подстановки g и p. Выражение обобщенной силы в уравнении Лагранжа, получение дифференциального уравнения малой вибрации b путем интегрирования этого уравнения и определения любой интегральной постоянной. Найти уравнение движения системы 6 и определить период колебаний и другие искомые величины.
Второй способ заключается в применении одного из основных уравнений динамики или 1 общей теоремы динамики Система 1 основана на условиях задачи, дифференциальных уравнениях-основных уравнениях динамики, теореме движения центра инерции, теореме изменения- Применяя выбранную теорему, теорему об изменении основного момента кинетической энергии, импульса 2, Составляем дифференциальное уравнение малых колебаний системы. 3 интегрируем это дифференциальное уравнение и определяем любую интегральную постоянную из исходных данных 4 находим далее искомую величину периода колебаний и покоя. Вопрос 18. 6.
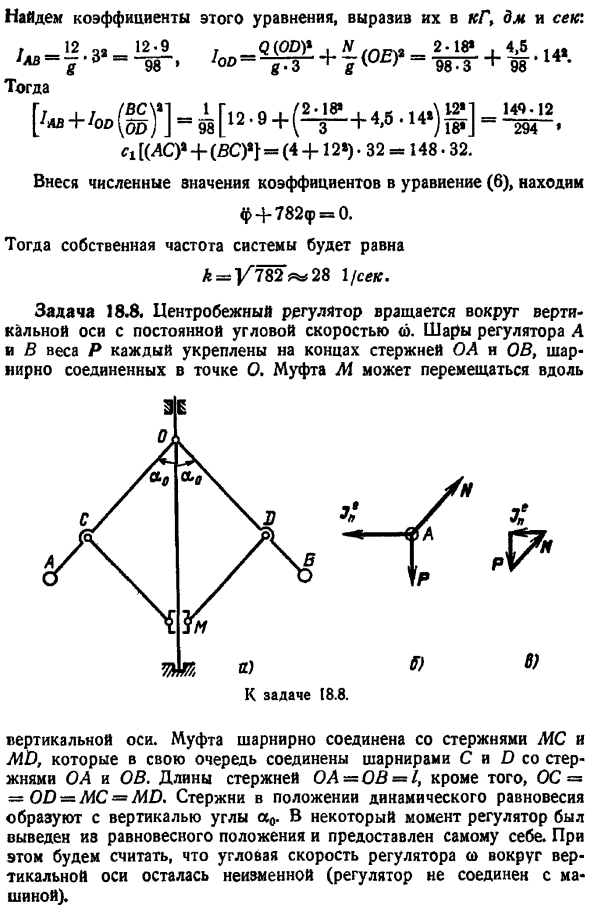
Устройство, предназначенное для определения коэффициента трения скольжения между сухими поверхностями, рис. а, прямоугольный металлический блок размещен горизонтально 2. Плоскость de на двух цилиндрах вращается в противоположных направлениях вокруг неподвижных осей a и b. Центр тяжести блока равен g, , , x a x задача 18. 6. Высота h от плоскости ДЕ. Расстояние ab 2a. At в первый момент центр тяжести сместился от центрального position. As в результате блок начал совершать гармонические колебания периодического g. Трение скольжения между блоком и обоими цилиндрами одинаково, найти коэффициент трения скольжения. Решение.
Мысленно отбросьте цилиндр и замените действие обычной реакцией rj. R2 и сила трения frlt frt рисунок b. Сила тяжести блока r приложена к центру тяжести. Создайте дифференциальное уравнение для плоского движения блока, учитывая, что блок не движется. Вдоль оси y и МЯс инерции вокруг центра, чтобы не вращаться — — -р, — Шmj c ri rj-p 0, 2 mra-х-riвхrift-frjh 0. 3 ри-л х ра РЖ хр откуда введите это значение в уравнение 1 и вы найдете дифференциальное уравнение движения r -, r 7s-tax.
Это дифференциальное уравнение для свободных гармонических колебаний. Периодичность этих колебаний равна 4пДgp 4n задача 18. 7, где искомый коэффициент трения скольжения определяется следующим уравнением рама балансировочной машины От рычага ab, который может вращаться вокруг неподвижной точки c, его центр тяжести, стержень bd и диск e будут соответствовать установленному валу od. Конец o. Концы рычагов a и b соединены вертикальной пружиной с неподвижным основанием. Вес Рычага АВ равен 12 г.
Радиус инерции к проходящей горизонтальной оси 3. Проходя через центр тяжести С, который равен dm. Вес q сечение вала od 2 кг является постоянным. Вес диска e составляет n 4, 5 кг. Коэффициент жесткости каждой пружины составляет cj 32 кг ДМ. Размеры ac 2 dm, ac 12 dm, oe m dm, de 4 dm определяют частоту собственных колебаний системы, игнорируя вес тяги bd. Масса диска считается сосредоточенной в точке Е. Для Чтобы найти собственную частоту системы, мы применяем уравнение Лагранжа. Система имеет 1 степень свободы. Выберите угол поворота рычага ab в качестве обобщенной координаты. Указывает этот угол q. Кинетическая энергия системы равна t-l. 1 выпуск, 18. 7.
Где 1lv-момент инерции Рычага АВ к горизонтальной оси через центроид С. od-неподвижный вал момент инерции вала od и угол поворота вала phx-od, вместе с диском установленным относительно горизонтальной оси до конца o. in небольшое движение Вертикальные перемещения точек b и d являются equal. So bc-tf является od-tf, дифференцируя 2 во времени и подставляя значение px в 1, кинетическая энергия равна Перейти к обобщенной скорости 3 обобщенный расчет силы. Горизонтальное положение рычага — это положение статического равновесия. Показывает угол поворота рычага ab Это соответствует переходу из ненапряженного состояния пружины в равновесное положение.
Бесконечно малое приращение bf от положения равновесия, направленное на угол По часовой стрелке, все показатели работы основания силы для 6a-cx ac 2 f f fst bf-cc rc f bf—n-oe-q-t h 6a-ci ac 1 f bf-cx df bf—g, pm 1, bc q. N-oe s q 6f 4, 2, согласно k sun od. Здесь основная работа упругих сил типа пружины а рассчитывается по формуле b ax-f bx-sa x xst bx-ciac f ac bf-ch acr f fet bf. By добродетель В уравнении равновесия угловые скобки 4 равны нулю, поэтому это 6a bf-ckf ac 1 bc 1 bf, а обобщенная сила q, — c1v ac 1 sc 2. To составьте уравнение b-Лагранжа Подставим значения кинетической энергии 3 и обобщенной силы из b. Получим ld iod j-Ф-cxac 1 bcpjФ.
- Найдите коэффициенты этого уравнения и выразите их в следующем порядке kg, dm, sec, c1 -КАК ac 4 12-32 148. 32. Вводя численное значение коэффициента в уравнение 6, находим f 782 p 0. Собственная частота системы v782 равна 28 1 секунде. Задача 18. 8. Центробежный регулятор вращается вокруг вертикальной оси с постоянной угловой скоростью. Регуляторы a и b веса p поворачиваются к концу стержня od n ob соответственно. Он соединен с точкой o. Муфта m может перемещаться вдоль вертикальной оси.
Муфта шарнирно соединена со стержнем mc и md и соединена со стержнем шарниром c и o. ПРО А и ОВ. Длина стержня oa-ov 1, далее os-0d mc md. Стержень в положении динамического равновесия образует вертикальную линию и угол a0. At в один момент регулятор отключился. Вышел из равновесия, предоставленный самому себе devices. In в этом случае угловая скорость регулятора w вокруг вертикальной оси не изменяется, и контроллер Найти период малых колебаний вблизи положения равновесия. Масса стержня и муфты игнорируется.
При относительном криволинейном движении материальной точки удобно пользоваться дифференциальными уравнениями движения в проекциях на оси натурального триэдра. Людмила Фирмаль
Мяч a и b рассматриваются как важные точки. Решение. Разделите раствор на 2 этапа. Во-первых, положение динамического равновесия системы определяется кинетическим методом statics. In Фаза 2, используя уравнение Лагранжа с обобщенными координатами Найти дифференциальное уравнение для малых колебаний системы и частоты и периода этих колебаний. Первая ступень. Примените метод статики движения к шару а в положении динамического равновесия. Шар фигура ТФ актов по тяжести Р, Шатун Н реакция направлена вдоль стержня АО. Согласно методу кинетической статики, эти силы должны компенсироваться силой инерции j.
При вращении с постоянной угловой скоростью c вокруг вертикальной оси существует только сила вертикальной инерции, равная по абсолютной величине j ml sin aoco, которая является массой шара. 3 Мощность jk p, n можно рассматривать как фигуру. tf. Создайте схему треугольника мощности. c, оттуда найти p tg 0 jn mzsinoofind. Отсюда, угол о Положение w 2-я стадия динамического равновесия. Дайте угол od, образованный стержнем с небольшим вертикальным шагом ba.
Шарик начинает мелко вибрировать Рядом с положением равновесия. Регулятор представляет собой систему с 2 степенями свободы. Возьмем обобщенный координатный угол a. Это позволит определить отклонение шарика и стержня Это угол от вертикали, где угол Р — угол поворота регулятора вокруг вертикальной оси. Создадим первое уравнение Лагранжа обобщенных координат a. Рассмотрим движение шара как составное Найти абсолютную скорость шара по переносному вращению вокруг вертикальной оси и теорему сложения относительной скорости вращения вокруг горизонтальной оси через точку o Переносные и относительные модули скорости такие же, как iv zsina o zsina-q, vr 1a.
Обратите внимание, что vr находится на плоскости, которая совпадает с ромб oabm, и v перпендикулярно этой плоскости. Г 2 В, П Ф2 грех 4-й. Кинетическая энергия 2 шаров равна 3. Перейдем к определению обобщенных сил. Вертикальные координаты шара z равны 2 zcosa. Его вариация-6z-zsinada. Основная задача гравитации, которая является единственной активной силой, приложенной к системе, 2r — это 6 a 2p dz-2p1 sin a ba. So обобщенная сила-это qa- 2pzsina. 4.
Если подставить найденную кинетическую энергию и обобщенные значения силы в уравнение Лагранжа, то получим dt да 2 f sin a cos a. 5 замена dt, согласно 2-му, b 2 вместо 7 2 atcsl w s f — — — — — — — — 2w ln и 6, или производная коэффициента, деленная на, а, noting-ш2sin aepcos a, Р-sin ao r найдена. 7 угол р, согласно условиям — Небольшое количество. В результате, грех А0 П и грех С С ко п п потому что, потому что ОО п потому что АО-psinctg, где примерно греха П и п, потому что п i1. By введя значение 8 и заменяя г л в cosпо 1 В уравнение 7, получаем 0-грех чч 0 А0 А0 А0 потому что потому что-0 грех куб. См 4-и cos СС Син о 0 потому что А0 0 или 0 СО2 грех аб0 грешить, потому что А0 00 0.
Потому что ao02 второй размер Для меньших порядков мы в конечном итоге находим дифференциальное уравнение свободных малых колебаний центробежного регулятора e, sin al 0 0. 9 частота свободных колебаний равна sin a, , В a. Период свободных малых колебаний был равен угловой скорости 10, и 2-е уравнение Лагранжа, соответствующее обобщенной координате р, не требовалось. Это и есть условие Задача изменяет набор координат.
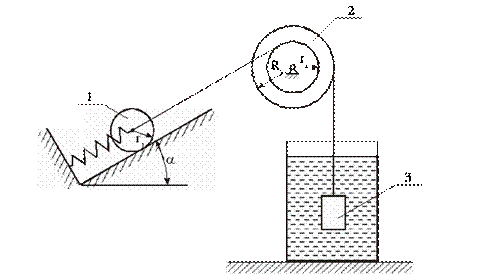
Его производная-регулятор постоянен при вращении вокруг вертикальной оси. Задача 18. 9. Груз веса Р подвешен нерасширении нить АБ. Он набрасывается сверху на блок с неподвижной осью o. Вес блока f. Его масса равномерно распределяется по поверхности круга с радиусом d. Конец резьбы b прикрепляется к вертикальной пружине, а коэффициент с одинаковой жесткостью. Определите изменение нагрузки.
Если в первый момент груз неподвижен, то его вес уравновешивается натяжением пружины, и сообщается начальная скорость v0 Трение между осью нисходящего блока и подшипником игнорируется. Вес нити игнорируется. Решение. Используйте 2-й вид уравнения Лагранжа. Выберите ось x начинается в положении равновесия груза и направляет его вертикально вниз. Тогда координата x нагрузки в любой момент времени полностью определяет положение системы. Это считается корректировкой сообщества.
Кинетическая энергия системы-это сумма кинетической энергии нагрузки и кинетической энергии агрегата. Скорость Груза Поскольку скорость и величина точек на ободе блока равны, окончательное представление кинетической энергии системы обобщенной скоростью принимает вид Дает системе возможное движение bx и составляет основную задачу данной мощности. Основная работа заключается в работе силы тяжести груза и силы упругости пружин 6Д П ЛК-ы х д р ВХ-х Д-в ы х ВХ-СБХ. В состоянии равновесия это СД Р.
Буква d указывает на статическое удлинение пружины. Обобщенная сила-это коэффициент, когда это возможно. Перемещение bx в начальной школе работа q формула. 1 заметим, что в этой задаче обобщенная сила q может быть легко вычислена другим способом. Давайте создадим выражение возможности Энергия системы выбора нулевого положения равновесия груз П. В свою очередь, Н-lr и обобщенной Си. 11 матчей 1. Создайте уравнение Лагранжа. Или потому что bt dx это решение Однородные линейные дифференциальные уравнения с постоянными коэффициентами имеют вид x a sin ktp, 2. Где частота a находится из уравнения p 0.
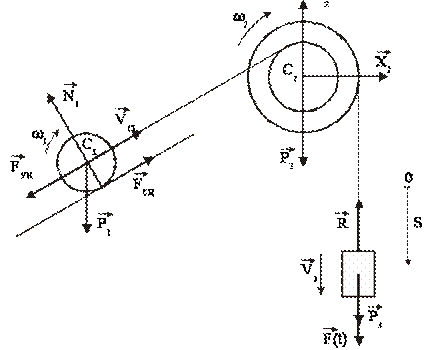
Любая постоянная Интегралы a и 0 определяются из начальных условий t 0, и существуют x0 0, jjg-og. Если вы присвоите эти значения 2, вы найдете oa sinp или р0. Затем из 2, чтобы получить Ак, потому что КТ введение значения любой константы при i0 t 0 ak или 2 в конечном итоге даст x в sin at. Цикл свободных колебаний нагрузки равен задаче 18. 10. Масса q и радиус Горсуча g удерживается в равновесии на идеально гладкой горизонтальной поверхности резьбой ab. In в этом случае плоская часть поверхности полусферы образует горизонт и угол. a. Определите после Обрыв резьбы ab, скорость центра o и ее максимальное, наибольшее давление полушария на горизонтальную плоскость.
Кроме того, предполагая, что угол a мал, длина становится короче Эквивалентный математический маятник. Решение. После того, как резьба нарезается, Рис. 2 силы действуют на всем полушарии. Это реакция веса q и гладкой плоскости Н. Обе силы направлены вертикально. Согласно теореме о движении центра инерции, ускорение центроида С также направлено вертикально. Начальная скорость точки С, а также других точек полушария Если она равна нулю, то центр инерции перемещается в вертикальном направлении по прямой линии. Центр полусферы o находится на некотором расстоянии r от гладкой плоскости. Перемещение по горизонтальной линии параллельно плоскости отсчета.
Таким образом, скорость точки с направлена вертикально, а скорость точки о направлена горизонтально. Восстановление до скорости 2 из этих 2 точек являются вертикальными, поэтому мы находим мгновенный центр скорости a b. Примените теорему изменения кинетической энергии для перемещения полушарий с самого начала Положение, определяемое углом a, при любом положении угла p получает 44 cos f-cos a представляет ОС. 1 слева от уравнения находится уравнение кинетической энергии В конце движения, в первый момент, кинетическая энергия ручара была равна нулю, потому что ручар был неподвижен.
На правой стороне рассчитана работа силы тяжести при переходе полушарий От начального положения до конечного положения. Эта реакция направлена перпендикулярно движению точки d, поэтому работа реакции n равна нулю. Момент инерции полусферы относительно момента Для ic tp sin8 p центр скорости может быть выражен на основе теоремы Штейнера следующим образом 2 Итак, если известна функция угла. Айкью-определить момент Инерция пола шара направлена к горизонтальной оси, которая проходит через центр инерции и перпендикулярна плоскости чертежа. Равномерный момент инерции шарика 2 0 Центральная ось равна 2 0-mg 2t g. Здесь m 2t-масса однородного шара.
Затем формируется равномерный момент инерции полусферы относительно горизонтальной оси, которая перпендикулярна плоскости чертежа Проходя через точку О, расстояние центра инерции полусферы от точки о равно zr 8. Используйте теорему Штайнера, чтобы создать это значение с помощью −1, -tp-a mr-iт И-Л. В уравнении 2 r mr tp sin r tr c sin f. Для краткости, если вы укажете 83 45 секунд, вы получите cozy-cos от 1 до 2g и s sin y 3 4 5. Скорость точки o центра половины шара равна тому же значению, что и v0 op. ВМ со ф потому что j в точке o скорость f 0.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Система со многими степенями свободы — справочник студента
Теория свободных колебаний систем с несколькими (s) степенями свободы строится аналогично тому, как было рассмотрено в одномерных колебаниях.
Пусть потенциальная энергия системы Uкак функция обобщенных координат qi ( i = 1, 2, . s )имеет минимум при qi = qi 0. Вводя малые смещения
и разлагая по ним Uс точностью до членов второго порядка, получим потенциальную энергию в виде положительно определенной квадратичной формы
где мы снова отсчитываем потенциальную энергию от ее минимального значения. Поскольку коэффициенты kikи kkiвходят в (3, 2) умноженными на одну и ту же величину xi xk,то ясно, что их можно всегда считать симметричными по своим индексам
В кинетической же энергии, которая имеет в общем случае вид
полагаем в коэффициентах qi = qi 0 и, обозначая постоянные aik ( qo )посредством mik ,получаем ее в виде положительно определенной квадратичной формы
- Коэффициенты mlk тоже можно всегда считать симметричными по индексам
- mik = mki
- Таким образом, лагранжева функция системы, совершающей свободные малые колебания:
Составим теперь уравнения движения. Для определения входящих в них производных напишем полный дифференциал функции Лагранжа
Поскольку величина суммы не зависит, разумеется, от обозначения индексов суммирования, меняем в первом и третьем членах в скобках i на k , a k на i;учитывая при этом симметричность коэффициентов mik и kik, получим:
Отсюда видно, что
Поэтому уравнения Лагранжа
- Они представляют собой систему s(i = l, 2, … , s)линейных однородных дифференциальных уравнений с постоянными коэффициентами.
- По общим правилам решения таких уравнений ищем s неизвестных функций xk(t)в виде
(3,6)
- где Аk — некоторые, пока неопределенные, постоянные. Подставляя (3,6) в систему (3,5), получаем по сокращении на систему линейных однородных алгебраических уравнений, которым должны удовлетворять постоянные Аk:
- (3,7)
- Для того чтобы эта система имела отличные от нуля решения, должен обращаться в нуль ее определитель
- (3,8)
- Уравнение (3,8)—так называемое характеристическоеуравнение — представляет собой уравнение степени s относительно ω2. Оно имеет в общем случае s различных вещественных положительных корней ω²a,
а=1, 2, … , s (в частных случаях некоторые из этих корней могут совпадать). Определенные таким образом величины ωа называются собственными частотамисистемы.
Вещественность и положительность корней уравнения (3,8) заранее очевидны уже из физических соображений.
Действительно, наличие у ω мнимой части означало бы наличие во временной зависимости координат х k (3,6) (а с ними и скоростей xk)экспоненциально убывающего или экспоненциально возрастающего множителя.
Но наличие такого множителя в данном случае недопустимо, так как оно привело бы к изменению со временем полной энергии E=U+T системы в противоречии с законом ее сохранения.
- В том же самом можно убедиться и чисто математическим путем. Умножив уравнение (3,7) на и просуммировав затем по i,получим:
- откуда
- Квадратичные формы в числителе и знаменателе этого выражения вещественны в силу вещественности и симметричности коэффициентов kik и mik ,действительно,
- Они также существенно положительны, а потому положительно и ω2.
После того как частоты ωа найдены, подставляя каждое из них в уравнения (3,7), можно найти соответствующие значения коэффициентов А k .
Если все корни ωа характеристического уравнения различны, то, как известно, коэффициенты Ak пропорциональны минорам определителя (3,8),в котором ω заменена соответствующим значением ωа, обозначим эти миноры через ∆ka. Частное решение системы дифференциальных уравнений (3,5) имеет, следовательно, вид
- где Са— произвольная (комплексная) постоянная.
- Общее же решение дается суммой всех s частных решений. Переходя к вещественной части, напишем его в виде
- (3,9)
- Где мы ввели обозначение
- (3,10)
- Таким образом, изменение каждой из координат системы со временем представляет собой наложение s простых периодических колебаний
- Θ1, Θ2, … , Θs с произвольными амплитудами и фазами, но имеющих вполне определенные частоты.
Естественно возникает вопрос, нельзя ли выбрать обобщенные координаты таким образом, чтобы каждая из них совершала только одно простое колебание? Самая форма общего интеграла (3,9) указывает путь к решению этой задачи.
В самом деле, рассматривая s соотношений (3,9) как систему уравнений с s неизвестными величинами Θа, мы можем, разрешив эту систему, выразить величины Θ1, Θ2, …, Θs через координаты x1, x2, …, xs .
Следовательно, величины Θа можно рассматривать как новые обобщенные координаты.
Эти координаты называют нормальными(или главными), а совершаемые ими простые периодические колебания — нормальными колебаниями системы.
Нормальные координаты Θа удовлетворяют, как это явствует из их определения, уравнениям
Это значит, что в нормальных координатах уравнения движения распадаются на s независимых друг от друга уравнений.
Ускорение каждой нормальной координаты зависит только от значения этой же координаты, и для полного определения ее временной зависимости надо знать начальные значения только ее же самой и соответствующей ей скорости. Другими словами, нормальные колебания системы полностью независимы.
Из сказанного очевидно, что функция Лагранжа, выраженная через нормальные координаты, распадается на сумму выражений, каждое из которых соответствует одномерному колебанию с одной из частот ωа, т. е. имеет вид
где та — положительные постоянные. С математической точки зрения это означает, что преобразованием (3,9) обе квадратичные формы — кинетическая энергия (3,3) и потенциальная (3,2) — одновременно приводятся к диагональному виду.
- Обычно нормальные координаты выбирают таким образом, чтобы коэффициенты при квадратах скоростей в функции Лагранжа были равны 1/2. Для этого достаточно определить нормальные координаты (обозначим их теперь Qa ) равенствами
- (3.13)
- Тогда
Все изложенное мало меняется в случае, когда среди корней характеристического уравнения имеются кратные корни. Общий вид (3,9), (3,10) интеграла уравнений движений остается таким же (с тем же числом s членов) с той лишь разницей, что соответствующие кратным частотам коэффициенты ∆k а уже не являются минорами определителя, которые, как известно, обращаются в этом случае в нуль.
Каждой кратной (или, как говорят, вырожденной) частоте отвечает столько различных нормальных координат, какова степень кратности, но выбор этих нормальных координат не однозначен.
Поскольку в кинетическую и потенциальную энергии нормальные координаты (с одинаковым ωа)входят в виде одинаково преобразующихся сумм можно подвергнуть любому линейному преобразованию, оставляющему инвариантной сумму квадратов.
- Весьма просто нахождение нормальных координат для трехмерных колебаний одной материальной точки, находящейся в постоянном внешнем поле. Помещая начало декартовой системы координат в точку минимума потенциальной энергии U ( x , y , z ), мы получим последнюю в виде квадратичной формы переменных х, у, z , а кинетическая энергия
- (т — масса частиц) не зависит от выбора направления координатных осей.
- Поэтому соответствующим поворотом осей надо только привести к диагональному виду потенциальную энергию. Тогда
- (3,14)
- и колебания вдоль осей х, у, z являются главными с частотами
- В частном случае центрально-симметричного поля (k 1= k 2= k 3= k , U = kr ²/2) эти три частоты совпадают.
- Использование нормальных координат дает возможность привести задачу о вынужденных колебаниях системы с несколькими степенями свободы к задачам об одномерных вынужденных колебаниях. Функция Лагранжа системы с учетом действующих на нее переменных внешних сил имеет вид
- (3,15)
- где L0 — лагранжева функция свободных колебаний. Вводя вместо координат хk нормальные координаты, получим:
- (3.16)
- где введено обозначение
- Соответственно уравнения движения
- будут содержать лишь по одной неизвестной функции Qa(t).
- Затухающие колебания
До сих пор мы всегда подразумевали, что движение тел происходит в пустоте или что влиянием среды на движение можно пренебречь. В действительности при движении тела в среде последняя оказывает сопротивление, стремящееся замедлить движение. Энергия движущегося тела при этом в конце концов переходит в тепло или, как говорят, диссипируется.
Процесс движения в этих условиях уже не является чисто механическим процессом, а его рассмотрение требует учета движения самой среды и внутреннего теплового состояния как среды, так и тела.
В частности, уже нельзя утверждать в общем случае, что ускорение движущегося тела является функцией лишь от его координат и скорости в данный момент времени, т. е. не существует уравнений движения в том смысле, какой они имеют в механике.
Таким образом, задача о движении тела в среде уже не является задачей механики.
Существует, однако, определенная категория явлений, когда движение в среде может быть приближенно описано с помощью механических уравнений движения путем введения в них некоторых дополнительных членов.
Сюда относятся колебания с частотами, малыми по сравнению с частотами, характерными для внутренних диссипативных процессов в среде.
При выполнении этого условия можно считать, что на тело действует сила трения, зависящая (для заданной однородной среды) только от его скорости.
Если к тому же эта скорость достаточно мала, то можно разложить силу трения по ее степеням.
Нулевой член разложения равен нулю, поскольку на неподвижное тело не действует никакой силы трения, и первый неисчезающий член пропорционален скорости.
Таким образом, обобщенную силу трения fтр, действующую на систему, совершающую одномерные малые колебания с обобщенной координатой х, можно написать в виде
- где а — положительный коэффициент, а знак минус показывает, что сила действует в сторону, противоположную скорости. Добавляя эту силу в правую сторону уравнения движения, получим :
- (4.1)
- Разделим его на m и введем обозначения
- (4.2)
ω0 есть частота свободных колебаний системы в отсутствие трения. Величина λназывается коэффициентом затухания. Таким образом, имеем уравнение
- (4.3)
- Следуя общим правилам решения линейных уравнений с постоянными коэффициентами, полагаем х — ert и находим характеристическое уравнение
- Общее решение уравнения (4.3) есть
- Здесь следует различать два случая.
- Если λ https://megalektsii.ru/s64576t11.html
Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы — импеданс и адмитанс, страница 15
Используя соотношения (3.56)
и выражения (3.54) видим, что при главных колебаниях имеют место соотношения
- Координаты ξ1
и ξ2 принятые в качестве обобщенных координат, называются
главными, или нормальными координатами. Для них система дифференциальных
уравнений распадается на два независимых уравнения ,
(3.58)
- Формы колебаний,
соответствующие главным координатам, обладают свойством, называемым
ортогональностью. Составим выражение
где (х1, θ1)
и (x2, θ2) — значения координат x, θ, соответствующие главным колебаниям.
На основании (3.57) можем
написать
Легко видеть, что выражение в
квадратных скобках равно нулю, так как из свойства квадратного уравнения (3.51)

что выражает свойство ортогональности форм
главных колебаний.
3.8. Связанные
собственные и вынужденные колебания
- систем со многими
степенямисвободы. - Динамические
характеристики простейших - механической системы и ее элементов
В подразделе 3.7 были описаны
некоторые общие свойства, характеризующие связанность колебаний на примере
системы, с двумя степенями свободы.
При определении частот и форм связанных
собственных колебаний систем с большим числом степеней свободы общие
классические методы, основанные на составлении частотных уравнений, становятся
громоздкими и не дают возможности легко получить практические результаты.
Для анализа таких систем в
настоящее время используются специальные, достаточно эффективные методы. К
таким методам относится метод, основанный на применении импеданса и адмитанса.
При применении этих методов сложная колебательная система расчленяется на ряд
более простых или простейших, для каждой из которых определяется динамическая
характеристика — импеданс или адмитанс, а затем с помощью этих характеристик
производится наращивание-присоединение одной системы к другой до тех пор, пока
не будет составлена вся система полностью.
Рассмотрим динамические
характеристики механической системы, связанные с действием на нее обобщенного
гармонического возбуждения, которое характеризуется зависимостями силы и
скорости от времени
P = P0 ejωt, V = V0ejωt
(3.60)
Представим оба вида
возбуждения, которые можно характеризовать как силовое и кинематическое
возбуждение. В первом из них задана сила с фиксированной амплитудой, во втором —
смещение с постоянной амплитудой скорости.
Рассмотрим системы, состоящие
из отдельных элементов: рис. 3.39, а — масса т, рис. 3.39, б
— элемент с трением, коэффициент rкоторого
пропорционален скорости, рис. 3.
39, в — упругий элемент с коэффициентомжесткости с.
При возбуждении гармонических колебаний этих элементов
имеются для них соответственно динамические характеристики —импеданси
адмитанс — отношение силы к скорости и наоборот:
 |
Рис. 3.39. Масса, элемент с трением и
упругость
Простые зависимости (3.30,
3.31), которые сводятся к прямой и обратной пропорциональности и к константе,
легко представить в логарифмическом масштабе в виде прямых линий (рис. 3.40, а,
б, в).
- Обобщенное кинематическое
возбуждение — это такое возбуждение - пары точек системы, при котором этим
точкам задано движение с относительной скоростью, равной Vejωt.
Рис. 3.40.
Адмитансы массы, демпфера и пружин
Обобщенным силовым
гармоническим — возбуждением системы называется возбуждение какой-либо пары
точек системы двумя равными и противоположно направленными силами Pejωt и —Pejωt.
ПОИСК
уравнения Лагранжа и пользуясь свойством симметрии в расположении рессор относительно продольной оси, получают следующие линейные диференциальные уравнения свободных колебаний надрессорного строения паровоза [c.
Как было показано в предыдущем параграфе, динамическая работа фундамента турбогенератора описывается системами со многими степенями свободы, требующими вычисления высших частот колебаний. В ряде случаев необходимо выяснить формы колебаний, что можно сделать, зная лишь точные значения частот.
Поэтому наиболее целесообразно решать эту задачу при помощи разложения в ряд векового уравнения движения материальных точек, позволяющего найти весь спектр частот собственных колебаний. Ранее практиковавшиеся способы расчета Л. 20, 21 и 29] не давали обобщенного решения, пригодного для определения колебаний в любом направлении. Ниже дан обобщенный способ решения.
Следует заметить также, что применение уточненных схем и точной методики расчета позволяет отказаться от так называемых условных значений частот собственных колебаний, благодаря чему отпадает условность расчетной методики.
[c.109]
Расчет по обеим указанным методикам может быть применен для фундаментов низкооборотных машин, в которых главная низшая частота собственных колебаний располагается близко к резонансной зоне. Для современных высокооборотных машин эти методики по той же причине дают удовлетворительные результаты для вертикальных колебаний. При расчете горизонтальных колебаний эти методики непригодны. Поэтому в [Л. 24— 29] был предложен более точный способ расчета. Здесь в методику расчета введены системы со многими степенями свободы, что позволило определить спектр частот собственных колебаний, из которого выбиралось значение частоты, наиболее близко расположенной к резонансной зоне. При этом из осторожности и опасения не-130
[c.130]
Как видно из указанного, принятый в [Л. 24 и 29] способ расчета хотя и является более точным, чем способ, изложенный в [Л. 20 и 21], благодаря применению новых, более правильных расчетных схем, однако его применение связано с введением целого ряда корректирующих коэффициентов и ограничений.
Как показали дальнейшие исследования, подсчитанные по изложенной выше методике частоты собственных колебаний и принятые расчетные схемы хорошо согласуются с экспериментальными данными. Это дало нам основание пересмотреть и уточнить методику расчета, изложенную в [Л.
29], освободив ее от введения корректирующих коэффициентов. В новой методике фундамент рассматривается как система со многими степенями свободы, подверженная действию возмущающих сил, изменяющихся по гармоническому закону с частотой, равной рабочим числам оборотов турбогенератора.
Величина этих возмущающих сил была определена в 3-1.
[c.131]
Учитывая, что при высокооборотных машинах наиболее близко расположенными к резонансной являются высшие частоты, резонансная зона которых очень узка, можно установить граничные значения резонансной зоны в пределах 10%- Вне этой зоны учитывать затухание нецелесообразно, так как, с одной стороны, оно оказывает незначительное влияние на величину амплитуды вынужденных колебаний, а, с другой стороны, в значительной степени усложняет расчет. Это в особенности относится к системе со многими степенями свободы.
[c.132]
Система со многими степенями свободы и проблема собственных значений
[c.45]
Уравнения движения системы со многими степенями свободы, записанные в матричной форме уравнений равновесия, имеют вид [c.45]
Для системы со многими степенями свободы ее отклик может быть разложен по собственным формам колебаний. В этом случае каждая форма будет обладать своей добротностью Q., а общая добротность системы определяется из выражения [c.303]
Прежде чем рассматривать колебательные системы со многими степенями свободы, напомним некоторые общие положения теоретической механики.
[c.29]
Переходя к колебаниям системы со многими степенями свободы вблизи положения равновесия, начнем, как и прежде, с рассмотрения нескольких частных случаев.
[c.54]
Общие уравнения системы со многими степенями свободы
[c.61]
Периоды свободных колебаний системы со многими степенями свободы. Свойство стационарности
[c.64]
Вынужденные колебания системы со многими степенями свободы. Принцип взаимности
[c.69]
Система со многими степенями свободы, колебания вынужденные 69
[c.372]
Булгаков Б. В., О применении метода Ван-дер-Поля к псевдо-лииейным системам со многими степенями свободы, ПММ 6, вып. 6 (1942).
[c.379]
Эта аналогия определяет специфическое название основных коэффициентов этого уравнения. Именно а называют квазиинерцион-ным коэффициентом, ас — квазиупругим коэффициентом. Эти названия сохраняются и при рассмотрении малых колебаний системы со многими степенями свободы.
[c.209]
Рождение устойчивого предельного цикла на торе означает синхронизацию колебаний ) — исчезновение квазииериодического и установление нового периодического режима.
Это явление, которое в системе со многими степенями свободы может произойти многими способами, препятствует возникновению режима, представляющего собой суперпозицию движений с большим числом несоизмеримых частот.
В этом смысле можно сказать, что вероятность реального осуществления именно сценария Ландау — Хопфа очень мала (этим не исключается, конечно, в частных случаях возможность возникновения нескольких несоизмеримых частот прежде, чем произойдет их синхронизация).
[c.162]
Системы со многими степенями свободы. Для того чтобы понять, какие качественные изменения вносит в движение упругой системы увеличение числа свободных координат, рассмотрим систему, изображенную на рис. 8.22, а.
Две равные массы nii и (rrii = m. =- т) скользят без трения по направляющей. Они связаны со стойкой и между собой пружинами, т. е. упругими связями. Жесткости крайних пружин одинаковы и равны k ki — k), жесткость средней обозначим через k Читайте также: Образование как система и процесс — справочник студента
При этом возрастание амплитуды колебаний системы происходит по показательному закону. Выражение (5.89) в этом случае определяет степень опасности комбинационного резонанса, когда спектральные плотности параметрических возмущений соответствуют, например, сейсмическим воздействиям в виде многоэкстремальных функций несущих частот, что особенно часто встречается на практике.
[c.219]
Ротор рассматривается как дискретная гироскопическая система со многими степенями свободы. Получен тип матрицы, отвечающей особенностям схемы, связанным с присутствием в ней продольных сил. Приводятся решения задачи в матричной форме для собственных и вын ткленных колебаний от неуравновешенности зонтичного ротора сложной структуры в поле сил тяжести.
[c.141]
Исполнительные механизмы роботов представляют собой проотран- ственные системы со многими степенями свободы, В Овдаи с этим исследование динамики роботов и манипуляторов представляет значительные трудности.
[c.11]
Графический способ определения частот собственных колебаний представляет 0П ре1делеиный интерес.
Однако в том виде, как он дан у Рауша, этот способ, с нашей точки зрения, недостаточно эффективен, так как частоты собственных колебаний системы с двумя степенями свободы значительно проще и точнее можно определить (путем раскрытая определителя векового уравнения (см.
3-3). Способ, предложенный Раушем, может стать эффективным только в том случае, если его распространить на системы со многими степенями свободы.
[c.202]
То, по какой конкретно из собственных форм происходит потеря устойчивости, зависит от конкретных сложившихся условий динамического взаимодействия рабочего колеса с потоком.
Эти условия зависят как от параметров потока и условий обтекания им ра-5бочих лопаток, так и от динамических свойств собственно рабочего колеса, проявляющихся через его спектр собственных движений и диссипативные особенности.
С повышением плотности спектра соб- ственных частот при наличии газодинамической связанности между лопатками вероятность возникновения автоколебаний возрастает, поскольку в зонах сгущения собственных частот рабочее колесо способно проявлять себя как система со многими степенями свободы, и этим облегчаются условия синтеза формы потери устойчивости в виде благоприятной суперпозиции множества независимых собственных форм, при которой системе потерять устойчивость наиболее удобно . В подобной ситуации потеря устойчивости сопровождается самосинхронизацией колебаний по различным собственным формам при амплитудно-фазовых их соотношениях, благоприятствующих потере устойчивости. Частота синхронных колебаний вблизи границы устойчивости близка к некоторой средней частоте сгущения собственных частот.
[c.141]
Динамическое состояние зубчатой передачи характеризуется в общем случае поведением ее как колебательной системы со многими степенями свободы.
Зубчатое колесо, сидящее на валу, имеет три степени свободы и, следовательно, возможны следующие колебания крутильные колебания колеса вокруг оси изгибные колебания (смещение) зубчатого колеса в плоскости зацепления, вызывающие деформации валов смещение зубчатого колеса в направлении, перпендикулярном к плоскости зацепления. В расчетах учитывают в основном крутильные колебания. С учетом степеней свободы связано число учитываемых при расчете колебательной системы сосредоточенных масс. Так как зубчатая передача обладает двумя или больпшм числом степеней свободы, то упрощенный расчет, использующий одномассовую заменяющую систему, только в некоторых случаях, может дать приемлемое решение.
[c.293]
Создать вибрационные машины как одномассные часто не удается по многим причинам (необходимо решить задачу виброизоляцин и др.). Однако при синтезе системы со многими степенями свободы использует те же идеи, что в случае синтеза одномассной системы [41].
В общем случае вибромашина может иметь несколько рабочих органов с разными технологическими задачами (в качестве второго рабочего органа можно рассматривать, например, и рукоятку вибромолотка, для которого идеальный закон движения х 0).
[c.
Измерение логарифмических декрементов колебаний. Декремент колебаний определяют различными способами. Требования к точности результата здесь в несколько раз ниже, чем при определении а°.
Большей частью приведенные внше способы измерения декремента одностепенной системы по ширине резонансных кривых (или по частотному годографу) пригодны н в случае системы со многими степенями свободы. Логарифмический декремент определяется попутно соотношениями (22) в процессе измерения а° при добавлении квадратурной составляющей сил возбуждения.
На практике проверяют, изменяется ли декремент 6° с изменением перемещения 9о- Зависимость 6J (i o) может быть найдена при измерениях 6 , на разных уровнях или по переходному процессу, вызванному мгновенным выключением гармониче» ского возбуждения выделенного тона.
При отсутствии биении декремент определяют-как указано выше для системы с одной степенью свободы, с усреднением за несколько (пять — десять) колебаний. Биений не будет при отсутетвии связи исследуемого тона с другими через силы демпфирования. Как правило, это относится к двум — трем низшим по частоте формам.
[c.341]
Выявление резонирующих элементов конструкций механизмов и блочных агрегатов при различном характере действующих сил.
В сложных колебательных системах со многими степенями свободы (например, в блочных агрегатах с присоединс ными опорными и неопорными связями) в диапазоне действия частот возбуждающи сил всегда имеется большое количество частот собственных колебаний, часто соь-падающих с частотами вынужденных колебаний, поэтому при определении резонансных характеристик механизмов и блочных агрегатов необходимо учитывать характер действующих в механизме сил.
[c.416]
Рассмотрим применение метода статистических испытаний при исследовании случайных колебаний многомассовой системы (рис. 3.9) при движении по дороге со случайными неровностями (проведено А. И. Котовым и Ю. Ю. Олешко). Одним из возможных путей снижения ускорений и ударов, действующих на транспортируемые грузы, является вторичная амортизация, т. е.
введение в систему груз — транспортное средство дополнительных упругих элементов и демпферов (амортизационных узлов). Основным внешним воздействием для наземных транспортных средств является кинематическое возмущение со стороны дороги, имеющее случайный характер (высота Н и длина волны дорожных неровностей X — случайные функции).
В случае неустановившегося движения для решения задачи о выборе параметров вторичной амортизации нельзя использовать спектральную теорию под-рессоривания, так как требуется определить вероятность пробоя системы амортизации, что можно сделать только, зная законы распределения перемещений.
Получить законы распределения выходных величин можно решением соответствующего данной многомерной задаче уравнения Колмогорова, что сделать для системы со многими степенями свободы очень сложно.
Кроме того, при решении уравнения Колмогорова получается многомерный закон распределения вектора состояния системы, который менее удобен при решении ряда задач (определение вероятности достижения заданной границы и т. д.), чем одномерные законы распределения компонент вектора состояния, получаемые методом статистических испытаний.
[c.101]
Мы можем изложить здесь общую теорию малых колебаний системы со многими степенями свободы лишь в общих чертах.
В случае одной степени свободы ( 7) оказалось возмон ным построить теорию, исходя из одного только уравнения энергии при наличии более чем одной зависимой переменной этого уравнения недостаточно и прпходптся снова обратиться к динамике.
Для простоты изложения предположим, что имеются только две Teneini свободы, однако изложение не будет содержать чего-либо, препятствующего непосредственному распространению его на общий случай.
[c.61]
http://lfirmal.com/svobodnye-kolebaniya-sistemy-s-odnoj-stepenyu-svobody-2/
http://school16rostov.ru/gumanitarnye/sistema-so-mnogimi-stepenyami-svobody-spravochnik-studenta.html


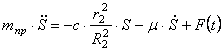

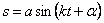

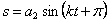

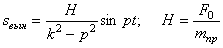



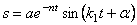



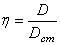













 (3,6)
(3,6)
 ,
,  (3.58)
(3.58)



