Структура общего решения линейного однородного дифференциального уравнения

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Данная статья рассматривает способы решения линейных дифференциальных однородных уравнений второго порядка с постоянными коэффициентами вида y » + p y ‘ + q y = 0 с p и q являющимися действительными числами. Будет рассмотрена теория с приведением примеров с подробным решением.

Перейдем к формулировке теоремы, которая показывает, какого вида должно быть уравнение, чтобы можно было искать общее решение ЛОДУ.

Теорема общего решения линейного однородного дифференциального уравнения

Общим решением линейного однородного дифференциального уравнения вида y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 0 ( x ) · y = 0 с непрерывными на интервале интегрирования x коэффициентами f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) определяют линейную комбинацию вида y 0 = ∑ j = 1 n C j · y j , где y j , j = 1 , 2 , . . . , n являются линейно независимыми частными решениями ЛОДУ на интервале x , где C j , j = 1 , 2 , . . . , n берут за произвольные постоянные.

Отсюда получаем, что общее решение такого уравнения y » + p y ‘ + q y = 0 может быть записано как y 0 = C 1 ⋅ y 1 + C 2 ⋅ y 2 , где y 1 и y 2 выражаются линейно независимыми решениями, а С 1 и C 2 – произвольными постоянными. Необходимо поработать с нахождением частных решений y 1 и y 2 .

Существует формула по Эйлеру для поиска частных решений вида y = e k · x .

Если взять y = e k · x за частное решение ЛОДУ второго порядка с постоянными коэффициентами y » + p y ‘ + q y = 0 , тогда, используя подстановку, получим тождество вида:

e k · x » + p · e k · x ‘ + q · e k · x = 0 k 2 · e k · x + p · e k · x + q · e k · x = 0 e k · x · ( k 2 + p · k + q ) = 0 k 2 + p · k + q = 0

Данное тождество называют характеристическим уравнением с постоянными коэффициентами k 1 и k 2 , которые и являются его решениями и определяют частые решения вида y 1 = e k 1 · x и y 2 = e k 2 · x заданного ЛОДУ.

При различных значениях p и q можно получить характеристические уравнения с корнами такого вида:

1. Действительные и различные k 1 ≠ k 2 , k 1 , k 2 ∈ R .
2. Действительные и совпадающие k 1 = k 2 , = k 0 , k 0 ∈ R .
3. Комплексно сопряженную пару k 1 = α + i · β , k 2 = α — i · β .

Первый случай показывает, что решениями такого уравнения могут быть y 1 = e k 1 · x и y 2 = e k 2 · x , а общее решение принимает вид y 0 = C 1 · e k 1 · x + C 2 · e k 2 · x с постоянными коэффициентами. Функции y 1 = e k 1 · x и y 2 = e k 2 · x рассматриваются, как линейно независимыми по причине отличного от нуля определителя Вронского W ( x ) = y 1 y 2 y 1 ‘ y 2 ‘ = e k 1 · x e k 2 · x k 1 · e k 1 · x k 2 · e k 2 · x = e k 1 · x · e k 2 · x · k 2 — k 1 с действительными k 1 ≠ k 2 , k 1 , k 2 ∈ R .

Второй случай объясняет, что первым частным решением функции – это выражение y 1 = e k 0 · x . Вторым частным решением можно брать y 2 = x · e k 0 · x . Определим, что y 2 = x · e k 0 · x может являться частным решением ЛОДУ второго порядка с постоянными коэффициентами y » + p y ‘ + q y = 0 и докажем линейную независимость y 1 и y 2 .

Имеем, что k 1 = k 0 и k 2 = k 0 являются совпадающими корнями характеристического уравнения. Тогда оно примет вид k — k 0 2 = 0 ⇔ k 2 — 2 k 0 · k + k 0 2 = 0 . Отсюда следует, что y » — 2 k 0 · y ‘ + k 0 2 · y = 0 является линейным однородным дифференциальным уравнением. Необходимо подставить выражение y 2 = x · e k 0 · x для того, чтобы убедиться в тождественности:

y 2 » — 2 k 0 · y ‘ 2 + k 0 2 · y 2 = 0 x · e k 0 · x » — 2 k 0 · x · e k 0 x ‘ + k 0 2 · x · e k 0 · x = 0 e k 0 · x + k 0 · x · e k 0 x ‘ — 2 k 0 · e k 0 · x + k 0 · x · e k 0 x + k 0 2 · x · e k 0 · x = 0 ( k 0 · e k 0 · x + k 0 · e k 0 · x + k 0 2 · x · e k 0 · x — — 2 k 0 · e k 0 · x — k 0 2 · x · e k 0 · x + k 0 2 · x · e k 0 · x ) = 0 0 ≡ 0

Отсюда следует, что y 2 = x · e k 0 · x — это частное решение данного уравнения. Необходимо рассмотреть линейную независимость y 1 = e k 0 · x и y 2 = x · e k 0 · x . Чтобы убедиться в этом, следует прибегнуть к вычислению определителя Вронского. Он не должен быть равен нулю.

W ( x ) = y 1 y 2 y 1 ‘ y 2 ‘ = e k 0 · x x · e k 0 · x e k 0 · x ‘ x · e k 0 · x ‘ = = e k 0 · x x · e k 0 · x k 0 · e k 0 · x e k 0 · x · ( 1 + k 0 · x ) = = e k 0 · x · e k 0 · x · 1 + k 0 · x — k 0 · x · e k 0 · x · e k 0 · x = e 2 k 0 · x ≠ 0 ∀ x ∈ R

Можно сделать вывод, что линейно независимые частные решения ЛОДУ второго порядка с постоянными коэффициентами y » + p y ‘ + q y = 0 считаются y 1 = e k 0 · x и y 2 = x · e k 0 · x . Это подразумевает то, что решением будет являться выражение y 0 = C 1 · e k 0 · x + C 2 · x · e k 0 · x при k 1 = k 2 = k 0 , k 0 ∈ R .

Третий случай говорит о том, что имеем дело с парой комплексных частных решений ЛОДУ вида y 1 = e α + i · β · x и y 2 = e α — i · β · x .

Запись общего решения примет вид y 0 = C 1 · e α + i · β · x + C 2 · e α — i · β · x .

Функции y 1 = e a · x · cos β x и y 2 = e a · x · sin β x могут быть записаны вместо частных решений уравнения, причем с соответствующими действительной и мнимой частями. Это понятно при преобразовании общего решения y 0 = C 1 · e α + i · β · x + C 2 · e α — i · β · x . Для этого необходимо воспользоваться формулами из теории функции комплексного переменного вида. Тогда получим, что

y 0 = C 1 · e α + i · β · x + C 2 · e α — i · β · x = = C 1 · e α · x · cos β x + i · sin β x + C 2 · e α · x · cos β x — i · sin β x = = ( C 1 + C 2 ) · e α · x · cos β x + i · ( C 1 — C 2 ) · e α · x · sin β x = = C 3 · e α · x · cos β x + C 4 · e α · x · sin β x

Отчетливо видно, что С 3 и С 4 используются в качестве произвольных постоянных.

Алгоритм нахождения общего решения линейного однородного дифференциального уравнения

Алгоритм нахождения общего решения линейного однородного дифференциального уравнения 2 порядка с постоянными переменными вида y » + p y ‘ + q y = 0 :

1. Запись характеристического уравнения k 2 + p ⋅ k + q = 0 .
2. Нахождение корней характеристического уравнения k 1 и k 2 .
3. Производим запись ЛОДУ, исходя из полученных значений с постоянными коэффициентами:

• y 0 = C 1 · e k 1 · x + C 2 · e k 2 · x при k 1 ≠ k 2 , k 1 , k 2 ∈ R ;
• y 0 = C 1 · e k 0 · x + C 2 · x · e k 0 · x при k 1 = k 2 = k 0 , k 0 ∈ R ;
• y 0 = e α · x · ( C 1 · cos β x + C 2 · sin β x ) при k 1 = α + i · β , k 2 = α — i · β .

Найти общее решение заданного уравнения с постоянными коэффициентами y » + 4 y ‘ + 4 y = 0 .

Решение

Следуя алгоритму, необходимо записать характеристическое уравнение k 2 + 4 ⋅ k + 4 = 0 , после чего обозначить его корни. Получаем, что

k 2 + 4 k + 4 = 0 ( k + 2 ) 2 = 0 k 1 = k 2 = k 0 = — 2

Очевидно, что полученные корни являются совпадающими.

Ответ: Запись общего решения: y 0 = C 1 · e k 0 x + C 2 · x · e k 0 x = C 1 · e — 2 x + C 2 · x · e — 2 x .

Найти решение заданного уравнения вида y » — 5 y ‘ + 6 y = 0 .

Решение

По условию имеется ЛОДУ 2 порядка с постоянными коэффициентами. Это указывает на то, что необходимо записать характеристическое уравнение и обозначить его корни. Получим:

k 2 — 5 k + 6 = 0 D = 5 2 — 4 · 6 = 1 k 1 = 5 — 1 2 = 2 k 2 = 5 + 1 2 = 3

Видно, что корни различные и действительные. Это говорит о том, что уравнение общего вида запишется как y 0 = C 1 · e k 1 x + C 2 e k 2 x = C 1 · e 2 x + C 2 · e 3 x .

Ответ: y 0 = C 1 · e k 1 x + C 2 e k 2 x = C 1 · e 2 x + C 2 · e 3 x .

Найти общее решение дифференциального уравнения вида y » — y ‘ + 3 y = 0 .

Решение

Необходимо перейти к характеристическому уравнению ЛОДУ 2 порядка, что соответствует записи k 2 — k + 3 = 0 , после чего обозначить его корни. Тогда получим, что

D = 1 2 — 4 · 3 = — 11 k 1 = 1 + i 11 2 = 1 2 + i · 11 2 k 2 = 1 — i 11 2 = 1 2 — i · 11 2 ⇒ α = 1 2 , β = 11 2

На выходе имеем пару комплексно сопряженных корней характеристического уравнения. Отсюда следует, что общим решением является запись уравнения вида

y 0 = e a · x · ( C 1 · cos β x + C 2 · sin β x ) = = e x 2 · C 1 · cos 11 x 2 + C 2 · sin 11 2

Ответ: y 0 = e x 2 · C 1 · cos 11 x 2 + C 2 · sin 11 2 .

Дифференциальные уравнения высших порядков 2

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

дифференциальное уравнение п-го порядка, разрешенное относительно старшей производной Возникает вопрос: какие надо задать условия, чтобы выделить определенное, частное решение уравнения (1)? Для дифференциального уравнения первого порядка достаточно задать значение уо частного решения при каком-то значении ж0 независимой переменной ж, т.е. задать точку (хо>Уо)> через которую должна проходить интегральная кривая этого уравнения. Для уравнений высшего порядка этого уже недостаточно.

Например, уравнение имеет решениями функции произвольные постоянные. Уравнение определяетдвухпараметрическое семейство прямых на плоскости хОу, и, чтобы выделить определенную прямую, мало задать точку (жо, Уо)» через которую прямая должна проходить, — надо еще задать угловой коэффициент прямой В общем случае дифференциального уравнения п-го порядка (1) для выделения частного решения надо задать п условий:

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ Задача Коши существование и единственности решения задачи Коши Уравнения высших порядков допускающие понижение порядка Линейные однородные Линейно зависимые и линейно независимые системы функций дифференциальные уравнения п-го порядка необходимое условие линейной зависимости определитель Вронского Структура общего решения линейного однородного дифференциального уравнения где некоторые числа.

Совокупность этих условий называется начальными условиями для дифференциального уравнения (1). Задача Коши для этого уравнения ставится так: найти решение дифференциального уравнения (1), удовлетворяющее заданным начальным условиям (2). Сформулируем теорему существования и единственности решения задачи Коши. Теорема 1 (существование и единственности решения задачи Коши). Пусть имеем дифференциальное уравнение п-го порядка, разрешенное относительно старшей производной.

Если правая часть этого уравнения непрерывна как функция п + 1 аргументов в некоторой окрестности (на рис. 1 для п = 2), то найдется интервал , на котором существует по крайней мере одно решение уравнения (1), удовлетворяющее начальным условиям Если, кроме того, функция п имеет ограниченные частные производными в указанной окрестности Q, то такое решение единственно.

Так, для уравнения правая часть рассматриваемая как функция трех независимых переменных г, у, у’. непрерывна всюду и имеет ограниченные всюду производные Поэтому, какова бы ни была тройка чисел , существует единственное решение этого уравнения, удовлетворяющее начальным условиям Определение.

Общим решением дифференциального уравнения п-го порядка в некоторой области Q существования и единственности решения задачи Коши вается n-параметрическое семейство 5 функций , зависящих от х и п произвольных постоянных , такое, что: 1) при любых допустимых значениях постоянных С\> С2. С„ функция является решением дифференциального уравнения (1), т. е. (лишь бы точка принадлежала области П существования и единственности решения задачи Коши для уравнения (1)), можно так подобрать значения постоянных, чтобы решение удовлетворяло заданным начальным условиям.

Решение, получаемое из общего при конкретных значениях постоянных , называется частным решением. Его график — кривую на плоскости хОу — называют интегральной кривой данного дифференциального уравнения. Соотношение , неявно определяющее общее решение, называют общим интегралом дифференциального уравнения (1). Задача. Показать, что функция является общим решением уравнения . Уравнения высших порядков, допускающие понижение порядка 1.

Возможно вам будут полезны данные страницы:

Уравнение вида где /(х) — известная непрерывная функция, интегрируется в квадратурах. Учитывая, что у(п) = (у(п_|)) , и интегрируя по х левую и правую части уравнения, получаем приходим к уравнению такого же вида, что и исходное; далее находим Через п шагов получим общее решение уравнения (1).

Пример 1:

Найти общее решение уравнения Л Последовательно интегрируя дважды, получаем искомое общее решение Если уравнение не содержит искомой функции и ее производных до порядка к — 1 включительно, т. е. имеет вид то порядок уравнения может быть снижен до порядка п-к заменой у^ = р(х). После такой замены уравнение принимает вид Пусть удалось проинтегрировать полученное уравнение: Замечая, что р = у^(х), приходим к уравнению из которого у(ж) находится fc-кратным интегрированием.

Пример 2:

Найти общее решение уравнения Положим , тогда и данное уравнение примет вид Разделяя переменные в последнем уравнении, найдем откуда легко получаем общее решение исходного уравнения: 3. Пусть дифференциальное уравнение не содержит явно независимой переменной ж, т.е. имеет вид Порядок этого уравнения можно понизить на единицу подстановкой у’ = р(у), где р = р(у) рассматривается как новая неизвестная функция, а у принимается за независимую переменную.

В этом случае все производные , к = 1,2, — , п, надо выразить через производные от функции р по у : Мы видим, что любая производная ^, к = 1,2. п, выражается через производные от р по у порядка не выше к-1, что приводит к понижению порядка уравнения на единицу. Пример 3. Проинтегрировать уравнение Положим . тогда и данное уравнение принимает вид Сокращая на , и разделяя переменные, найдем Всегда следует посмотреть, не является ли левая часть данного уравнения полным дифференциалом некоторого выражения.

Так, уравнение (*) можно переписать в виде откуда находим: Часто встречающееся уравнение можно легко проинтегрировать в квадратурах, если умножить обе его части на у’ (проделайте это!). Замечание 1. Рассмотрим уравнение второго порядка линейное относительно искомой функции у(х) и ее производных у’ и у». Положим где и(х), v(x) — новые функции, из которых одну мы можем выбирать произвольно.

Подставляя у(х) в форме (5) в исходное уравнение (4), для функции и(х) получаем уравнение Если известно одно решение yi(x) £ 0 исходного уравнения (4), то можно взять v = yi(x).

В уравнении (6) тогда исчезнет слагаемое, содержащее функцию и(х) (если , то так как, по предположению, yi (х) — решение уравнения (4)). Уравнение (6) примет тогда вид и легко интегрируется. В результате мы найдем обшее решение исходного уравнения (4). Если положить то в уравнении (6) исчезнет слагаемое с первой производной, и уравнение примет вид Такое преобразование полезно для качественного анализа уравнения и при использовании приближенных методов решения.

Рассмотрим, например, дифференциальное уравнение Бесселя числовой параметр, (8) (его решения — функции Бесселя — играют важную роль во многих задачах физики); представим его в виде Здесь , так что в силу (7) имеем Полагая . получаем для и(х) уравнение весьма удобное для изучения поведения функций Бесселя при больших значениях х. Замечание 2.

При решении задачи Коши для уравнений высших порядков бывает целесообразно определять значения постоянных С,- в процессе решения, а не после нахождения общего решения уравнения. Это связано с тем, что интегрирование порой значительно упрощается, когда постоянные С, принимают конкретные числовые значения, в то время как при произвольных С,- интегрирование затруднительно, а то и вообще невозможно в элементарных функциях. Рассмотрим, например, следующую задачу Коши:

Полагая получаем откуда , или Разделяя переменные, найдем В правой части последнего равенства имеем интеграл от дифференциального бинома. Здесь m = 0, л = 4, р = -1, так что этот интеграл не выражается в виде конечной комбинации элементарных функций. Однако если использовать начальные условия, то С\ = 0. Это сразу дает откуда, учитывая начальные условия, находим Задача. Найти два решения задачи Коши для уравнения с начальными условиями .

Не противоречит ли этот факт теореме существования и единственности решения задачи Коши? §3. Линейные однородные дифференциальные уравнения п-го порядка Линейным дифференциальным уравнением п-го порядка называется уравнение, линейное относительно неизвестной функции и всех ее производных. Оно имеет вид — заданные на некотором интервале (а, (5) функции. Если д(х) = 0 на этом интервале, то уравнение называется линейным однородным, в противном случае уравнение называется неоднородным.

Пусть имеем линейное однородное дифференциальное уравнение Если Оо(ж) ф 0 на некотором интервале, то разделив все члены данного уравнения на коэффициент ао(ж), получим Если коэффициенты п, уравнения (1) непрерывны на отрезке [а, 6|, то правая часть уравнения (2) непрерывна по для любых значений и, кроме того, имеетчастные производные по у^, равные ограниченные на [а, 6]. Поэтому в силу теоремы 1 получаем: если коэффициенты п, уравнения (1) непрерывны на [а, Ъ], то, каковы бы ни были начальные условия

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ Задача Коши существование и единственности решения задачи Коши Уравнения высших порядков допускающие понижение порядка Линейные однородные Линейно зависимые и линейно независимые системы функций дифференциальные уравнения п-го порядка необходимое условие линейной зависимости определитель

Вронского Структура общего решения линейного однородного дифференциального уравнения существует единственное решение уравнения (1), удовлетворяющее этим начальным условиям. Напомним следующее понятие. Говорят, что на множестве Е задан оператор Л со значениями в множестве F, если каждому элементу у 6 Е по некоторому закону поставлен в соответствие определенный элемент / = Лу 6 F. Множество Е называют областью определения оператора Л. Пусть Е — линейное пространство.

Оператор Л:

заданный на Еу называется линейным, если он аддитивен и однороден, где а — число. Представим линейное однородное уравнение (1) в виде Нетрудно видеть, что С есть линейный дифференциальный оператор, определенный на линейном пространстве функций у(ж), непрерывных на интервале (а, Ъ)% вместе со всеми производными до n-го порядка включительно.

Дифференциальный характер оператора очевиден. Покажем его линейность, т. е. что Как следствие получаем Установим некоторые свойства решений линейного однородного уравнения. Теорема 2. Если функция уо является решением линейного однородного дифференциального уравнения то функция Суо(х), где С — произвольная постоянная, тоже является решением этого уравнения.

По условию, Надо доказать, что Пользуясь свойством однородности оператора £[у], имеем Это означает, что функция Суо(х) есть решение уравнения Теорема 3. Если функции у\(х) и У2(х) являются решениями линейного однородного уравнения . Надо доказать, что Последнее сразу вытекает из свойства аддитивности оператора : Следспие. Линейная комбинация с произвольными постоянными коэффициентами решений линейного однородного дифференциального уравнения является решением того же уравнения.

Линейное однородное дифференциальное уравнение С[у\ = 0 всегда имеет тривиальное решение у = 0. Из теорем 2 и 3 получаем: совокупность решений линейного однородного дифференциального уравнения С[у\ = 0 образует линейное пространство, нулем которого является функция у = 0. Теорема 4. Если линейное однородное уравнение с действительными коэффициентами п, имеет комплексное решение то действительная часть этого решения и(х) и его мнимая часть v(x) в отдельности являются решениями того же однородного уравнения.

свойствами линейности оператора получаем Отсюда следует, что так как комплекснозначная функция действительного аргумента обращается тождественно в нуль тогда и только тогда, когда ее действительная и мнимая части тождественно равны нулю. Линейно зависимые и линейно независимые системы функций Пусть имеем систему функций . определенных на некотором интервале Определение.

Будем говорить, что система функций линейно зависима на интервале если существуют постоянные ап такие, что на этом интервале выполняется тождество по х: причем хотя бы одно из чисел отлично от нуля. Если это тождество имеет место только при а, то семейство функций ) называется линейно независимым на интервале (а, Ь).

Рассмотрим примеры линейно зависимых и линейно независимых систем функций. 1. Функции линейно зависимы на любом интервале (а, Ь), так как имеет место, например, тождество 2. Функции линейно независимы на любом интервале (а, 6), так как тождество возможно лишь в случае, если 4 Если хоть одно из чисел а, было бы отлично от нуля, то в левой части тождества стоял бы многочлен степени не выше п, который может иметь не более п различных корней и. следовательно, обращается в нуль не более чем в п точках рассматриваемого интервала.

3. Функции , линейно независимы на любом интервале (а, Ь). Для простоты ограничимся случаем п = 3. Допустим, что функции являются линейно зависимыми. Тогда имеет место тождество причем хотя бы одно из Qj не равно нулю. Пусть для определенности aj Ф 0. Разделив тождество на ек,х и продифференцировав, получим тождество деля которое на и дифференцируя результат по х. найдем что невозможно, так как аз Ф 0 по предположению .

Значит, наше допущение неверно, и рассматриваемые функции являются линейно независимыми. Замечание. Линейная зависимость пары функций означает, что одна из функций получается из другой умножением на постоянную: Вообще, если функции линейно зависимы на (а, 6), то по крайней мере одна из них сеть линейная комбинация остальных. Задача.

Показать, что если система функций линейно независима на интервале (а, Ь), то и любая подсистема этой системы функций также линейно независима на (а, 6). Теорема 5 (необходимое условие линейной зависимости функций). Если функции , имеющие производные до порядка п — 1 включительно, линейно зависимы на интервале (а, Ь), то на этом интервале определитель называемый определителем Вронского системы функций тождественно равен нулю: М Ограничимся случаем п = 3.

Пусть дважды дифференцируемые функции yi(x), У2(х), Уз(з) линейно зависимы на интервале (о, Ь). Значит, на (о, Ь) выполняется тождество причем не все числа a, (i = 1,2,3) равны нулю. Для определенности будем считать, что c*i Ф 0. Разрешим тождество относительно yi(s) и дважды продифференцируем его: Составим определитель Вронского системы функций Первый столбец определителя является линейной комбинацией двухдругих при любом х G (а, Ь).

Такой определитель, как известно, равен нулю; следовательно, Рассуждением от противного легко доказывается следующая теорема. Теорема 6. Если определитель Вронского W(x) системы п функций неравен тождественно нулю в некотором интервале (а, Ъ), то эти функции линейно независимы в этом интервале. или, с учетом формул (1) и (2), Для произвольной системы п — 1 раз дифференцируемых на (а, Ъ) функций теорема, обратная теореме 5, неверна. Чтобы убедиться в этом, рассмотрим пример. Для функций (рис. 2) определитель Вронского на интервале (-1,1) тождественно равен нулю:

Однако, как легко видеть, функции на интервале (-1,1) линейно независимы. Заметим, что в интервалах (-1,0) и (0,1) функции уже линейно зависимы. Можно несколько обобщить рассмотренный пример, взяв систему функций Эти функции линейно независимы в любом интервале, содержащем внутри себя точку х = 0, а вместе с тем их определитель Вронского тождественно равен нулю.

При этом, скажем, функция ^(х) имеет всюду непрерывные производные, до порядка m — 1 включительно, и лишь производная т-со порядка терпит разрыв с конечным скачком в точке х = 0. Выбирая m достаточно большим, получаем систему функций, обладающих непрерывными производными любого нужного порядка. Задана. Что можно сказать об определителе Вронского системы функций если только известно, что эти функции а) линейно зависимы; б) линейно независимы?

Теорема 7 (необходимое условие линейной независимости решений). Если линейно независимые на интервале (а, Ь) функции являются решениями линейного однородного дифференциального уравнения с непрерывными на [а, Ь\ коэффициентами р*(х), то определитель Вронского этой системы решений не может обратиться в нуль ни в одной точке интервала (а, 6). м

Ограничимся рассмотрением случая п = 3. Допустим, что в некоторой точке хо € (a, b) определитель Вронского равен нулю: Составим систему трех линейных однородных алгебраических уравнений относительно Определитель этой системы W(xq) в силу допущения равен нулю, поэтому система имеет ненулевое решение по крайней мере одно из чисел а, отлично от нуля. Рассмотрим функцию Она является линейной комбинацией решений уравнения (3), и, значит, сама есть решение этого уравнения.

Это решение в силу уравнений (4) удовлетворяет нулевым начальным условиям Таким начальным условиям, очевидно, удовлетворяет тривиальное решение у = 0 уравнения (3) и, по теореме о единственности решения, только это решение. Следовательно, причем хотя бы одно из oti отлично от нуля. Таким образом, решения оказываются вопреки условию теоремы линейно зависимыми.

Противоречие возникло в связи с допущением, что W(x) обращается в нуль в точке хо € (в, Ь). Значит, наше допущение неверно, и W(x) Ф 0 всюду в интервале (а, Ъ). Из теорем 5 и 7 как следствие получаем следующую важную теорему. Теорема 8. Для того, чтобы частные решения линейного однородного дифференциального уравнения (3) с непрерывными на отрезке [а, 6] коэффициентами были линейно независимыми на интервале (а, 6), необходимо и достаточно, чтобы определитель Вронского W(x) системы решений был отличен от нуля.

4 Необходимость условия прямо следует из теоремы 7. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ Задача Коши существование и единственности решения задачи Коши Уравнения высших порядков допускающие понижение порядка Линейные однородные Линейно зависимые и линейно независимые системы функций дифференциальные уравнения п-го порядка необходимое условие линейной зависимости определитель Вронского Структура общего решения линейного однородного дифференциального уравнения.

Задача. Показать, что два линейно независимых решения уравнения с непрерывными на отрезке [а, 6] коэффициентами не могут обращаться в нуль при одном и том же значении х0 €(о,6). §5. Структура общего решения линейного однородного дифференциального уравнения Теорема 9 (о структуре общего решения линейного однородного дифференциального уравнения).

Общим решением в области , линейного однородного дифференциального уравнения с непрерывными на отрезке коэффициентами , является линейная комбинация п линейно независимых на интервале (а, Ь) частных решений этого уравнения (С,, С2. ,Сп — произвольные постоянные). Будем исходить из определения общего решения и просто проверим, что семейство функций 1 удовлетворяет условиям 1), 2) этого определения.

Функция у(ж), определенная формулой (2), является решением дифференциального уравнения (1) при любых значениях постоянных Это следует из того, что, как было установлено выше, любая линейная комбинация частных решений линейного однородного уравнения есть снова решение этого уравнения. Для уравнения (1) при х 6 [а, Ь] выполнены условия теоремй 1 существования и единственности решения задачи Коши; поэтому остается показать, что постоянные C|, С2>. С„ всегда можно подобрать так, чтобы удовлетворялись произвольно заданные начальные условия Ограничимся случаем, когда п = 3.

Потребовав, чтобы решение удовлетворяло поставленным начальным условиям, получим систему трех линейных алгебраических уравнений относительно Определитель этой системы есть определитель Вронского W(x0) линейно независимой системы решений однородного уравнения (1), и, следовательно, отличен от нуля при любом х € (а, 6), в частности при х = xq. Поэтому система уравнений (3) однозначно разрешима относительно Сь C2i С3 при любом хо € (а, Ь) и при любых правых частях, т. е. при любых . А это и означает возможность выбора таких значений , чтобы частное решение удовлетворяло поставленным начальным условиям, каковы бы они ни были.

Из теоремы 9 следует, что если известно п линейно независимых частных решений линейного однородного дифференциального уравнения n-го порядка, то всякое другое решение этого уравнения представляется в виде линейной комбинации этих частных решений и, значит, линейно зависимо с ними. Отсюда вытекает, что максимальное число линейно независимых решений однородного линейного дифференциального уравнения равно его порядку.

Таким образом, совокупность решений линейного однородного дифференциального уравнения образует линейное пространство, размерность которого равна порядку дифференциального уравнения. Введем понятие фундаментальной системы решений. Определение. Совокупность любых п линейно независимых частных решений линейного однородного дифференциального уравнения п-го порядка называется его фундаментальной системой решений.

Теорема 10. У каждого линейного однородного уравнения (1) с непрерывными коэффициентами Рк(х) существует фундаментальная система решений (и даже бесконечное множество фундаментальных систем решений). В самом деле, рассмотрим, например, однородное уравнение второго порядка с непрерывными на отрезке [а, 6] коэффициентами. Пусть . По теореме 1 уравнение (4) имеет решения удовлетворяющие при х = xq начальным условиям.

Определитель Вронского в точке xq системы решений (5) отличен от нуля, Следовательно, система решений (5) для уравнения (4) фундаментальна. Выбор начальных условий (5′) обеспечил построение одной фундаментальной системы. За начальные данные в точке хо можно взять любую систему чисел: лишь бы определитель Вронского был отличен от нуля. Очевидно, таких систем чисел можно подобрать бесконечно много и построить бесконечно много фундаментальных систем решений для уравнения (4).>

Задана. Составить общее решение уравнения если известно ненулевое частное решение у\(х) этого уравнения. Теорема 11. Если два уравнения вида непрерывны на отрезке [а, Ь), имеют общую фундаментальную систему решений то эти уравнения совпадают, на отрезке [а, Ь\. Таким образом, фундаментальная система решений вполне определяет линейное однородное уравнение (1), т.е. полностью определяет коэффициенты , этого уравнения.

Следовательно, можно поставить задачу о нахождении уравнения вида (1), имеющего заданную фундаментальную систему решений Представим дифференциальное уравнениес левой частью в виде определителя: где у(х) — искомая функция, — заданная фундаментальная система решений. Уравнение (6) имеет в качестве решений функции так как при подстановке вместо у(х) каждой из этих п функций два столбца определителя становятся тождественно равными и определитель обращается в нуль тождественно по х 6 (а, 6).

Разлагая определитель по элементам последнего столбца, получаем из (6) уравнение вида определитель Вронского системы функций Определитель Вронского W(x) фундаментальной системы решений отличен от нуля во всем интервале (а, Ь). Разделив все члены уравнения приведем это уравнение к виду (1): где, в частности, Можно показать, что если элементы а1; определителя Д п-го порядка есть дифференцируемые функции аргумента х: то производная определителя равна сумме п определителей:

где — определитель, получающийся изданного заменой элементов его fc-ой строки производными от этих элементов. Например, для определителя Вронского системы функций Нетрудно проверить, что Ж|(ж) = ; следовательно, Интегрируя последнее равенство по х от хо до х, получим формулу Остроградского— Лиувилля:

Задача. Составить линейное дифференциальное уравнение второго порядка, имеющее решения Показать, что функции х, х2 линейно независимы на интервале (-оо, +оо). Убедиться в том, что определитель Вронского для этих функций равен нулю в точке х = 0. Почему это не противоречит необходимому условию линейной независимости системы решений линейного однородного дифференциального уравнения?

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Структура общего решения линейного однородного дифференциального уравнения

Т.о., для того, чтобы получить общее решение однородного уравнения (2), достаточно найти любые два линейно независимых частных решения этого уравнения (в этом случае говорят, что они образуют фундаментальную системурешений уравнения (2)).

множество) уравнения у′′ + у = 0 образуют фундаментальную систему решений.

Общим решением уравнения у′′ + у = 0 является функция у = С₁sin x + С₂cos x.

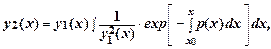В некоторых случаях удается тем или иным способом (например, подбором) найти только одно частное решение у₁(х). Тогда второе частное решение у₂(х) можно найти по формуле

Замечание. Сказанное выше распространяется на линейные однородные диф.уравнения n-го порядка

2. Функции у₁, у₂, … , у_n называются линейно независимыми на (a, b), если равенство

3. Определитель Вронского имеет вид W(x) = .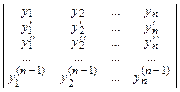

4. Частные решения у₁, у₂, … , у_n уравнения (4) образуют фундаментальную систему решений на

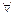
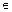
(a, b), если ни в одной точке этого интервала вронскиан не обращается в нуль, т.е. W(x) ≠ 0 х (a, b).

5. Общее решение линейного однородного дифференциального уравнения (4) имеет вид

где C_i (i = 1, 2, … , n) – произвольные постоянные, у_i – частные решения уравнения (4),

образующие фундаментальную систему.

Дата добавления: 2017-11-21 ; просмотров: 1436 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ