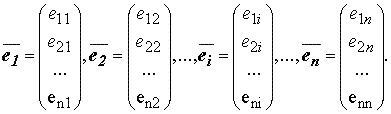Структура общего решения линейной системы дифференциальных уравнений

Линейные системы дифференциальных уравнений с постоянными коэффициентами

Линейные системы дифференциальных уравнений с постоянными коэффициентами

1. Общий вид линейной системы дифференциальных уравнений. Однородные и неоднородные системы. Случаи системы с постоянными коэффициентами

2. Основные свойства линейной системы дифференциальных уравнений

3. Основные способы решения однородной линейной системы

4. Понятие о фундаментальной системе решений однородной линейной системы

5. Построение общего решения однородной линейной системы по фундаментальной системе решений

6. Построение фундаментальной системы решения однородной системы с постоянными коэффициентами методом Эйлера

7. Структура общего решения неоднородной линейной системы

1. Общий вид линейной системы дифференциальных уравнений. Однородные и неоднородные системы. Случаи системы с постоянными коэффициентами

Для решения многих задач математики, физики, техники (задач динамики криволинейного движения; задач электротехники движения; задач электротехники для нескольких электрических цепей; определения состава системы, в которой протекают несколько последовательных химических реакций I порядка; отыскания векторных линий поля и других) нередко требуется несколько функций. Нахождение этих функций может привести к нескольким дифференциальным уравнении ям (ДУ), образующим систему.

Системой ДУ называется совокупность ДУ, каждое из которых содержит независимую переменную, искомые функции и их производные.

Нормальной системой линейных ДУ с действительными коэффициентами, называется система вида:

или более коротко

(2)

где — действительная матрица, а — действительный вектор, определенный при .

Однородной системой линейных уравнений, соответствующей системе (2), называется система уравнений

(3)

Система линейных дифференциальных уравнений с постоянными коэффициентами имеет вид

, (1.1)

где — -мерный вектор, — постоянная квадратная матрица размера .

2. Основные свойства линейной системы дифференциальных уравнений

Теорема 1. Линейная комбинация решений однородной системы (3) также является решением этой системы.

Теорема 2. Разность любых двух решений неоднородной системы уравнений (2) есть решение однородной системы (3).

Сумма любого частного решения неоднородной системы (2) и решения соответствующей однородной системы (3) есть решение неоднородной системы (2).

Теорема 3. Если и — решения систем уравнений

— решение системы уравнений

.

Теорема 4. Пусть () – решение системы уравнений (2), матрица и вектор непрерывны на отрезке . Пусть (где означает норму матрицы : ) и . Тогда для имеет место следующая оценка:

(4)

В частности, для линейной однородной системы (3) имеем оценку ():

(5)

Теорема 5. Пусть матрица системы (2) непрерывна на отрезке и . Тогда решение системы (2) однозначно определяется на отрезке условием

. (6)

Итак, из оценки (5) вытекает единственность решения задачи Коши для линейной системы (2) с непрерывной матрицей .

Следствие 1. Пусть матрица непрерывна на отрезке , тогда и для решения однородной системы (3) имеет место оценка

(7)

Иначе говоря, рост функции ограничен экспонентой.

Следствие 2. Решение однородной линейной системы с непрерывной матрицей тождественно равно нулю, если оно равно нулю в какой либо точке отрезка .

3. Основные способы решения однородной линейной системы

Линейные системы можно интегрировать различными способами, например методом исключения, путем нахождения интегрируемых комбинаций и т. д.

Для интегрирования однородных линейных систем с постоянными коэффициентами применяется метод Эйлера, который будет рассмотрен ниже.

4. Понятие о фундаментальной системе решений однородной линейной системы

Определение 1. Решения однородной системы (3) называются линейно независимыми на отрезке , если в каждой точке векторы линейно независимы.

Пусть задана система решений однородной системы (3), определенных на :

() (8)

Определение 2. Определитель

(9)

называется определителем Вронского системы решений .

Определение 3. Система из решений однородной системы уравнений (3), линейно независимых на отрезке называется фундаментальной.

5. Построение общего решения однородной линейной системы по фундаментальной системе решений

Определение 4. Общим решением линейной системы уравнений (2) называется множество всех решений этой системы.

Теорема 8. Пусть — фундаментальная система решений однородной системы уравнений (3), тогда формула

(15) где — произвольные постоянные, дает общее решение этой системы. Множество всех решений однородной системы уравнений (3) образует -мерное векторное пространство, базисом которого может служить любая фундаментальная система решений.

6. Построение фундаментальной системы решения однородной системы с постоянными коэффициентами методом Эйлера

Система линейных дифференциальных уравнений с постоянными коэффициентами имеет вид

, (1.1)

где — -мерный вектор, — постоянная квадратная матрица размера .

Метод Эйлера заключается в следующем. Решение системы (1.1) ищем в виде

,. (2.1)

Функция (2.1) является решением системы (1.1), если — собственное значение матрицы , а — собственный вектор этой матрицы, соответствующий числу . Если собственные значения матрицы попарно различны и — соответствующие собственные векторы этой матрицы, то общее решение системы уравнений (1.1) определяется формулой

,

где — произвольные числа. Если для кратного собственного значения матрицы имеется столько линейно независимых собственных векторов , какова его кратность, то ему соответствуют линейно независимых решений исходной системы: .

Если для собственного значения кратности имеется только линейно независимых собственных векторов, то решения, соответствующие , можно искать в виде произведения векторного многочлена степени на , т. е. в виде

.

Чтобы найти векторы , надо подставить выражение (2.1) в систему (1). Приравняв коэффициенты в левой и правой частях системы, получим уравнения для нахождения векторов .

Если среди собственных чисел матрицы имеются комплексные числа, то указанным выше методом строится соответствующее такому собственному числу решение системы (1.1) через комплексные функции. Чтобы выразить решение через действительные функции (в случае действительной матрицы ), надо воспользоваться тем, что вещественная и мнимая части комплексного решения, соответствующего собственному числу (), являются линейно независимыми решениями.

7. Структура общего решения неоднородной линейной системы,

Пусть — частное решение неоднородное решение неоднородной системы уравнений (2), а — фундаментальная система решений однородной системы уравнений (3). Тогда формула

, (16)

где — произвольные постоянные, дает общее решение неоднородной системы уравнений (2).

Теорема 9. Пусть на отрезке матрица и вектор непрерывны, и пусть известна фундаментальная система решений для однородной системы уравнений (3). Тогда общее решение неоднородной системы уравнений (2) находится с помощью квадратур.

Доказательство. Пусть — фундаментальная система решений для уравнения (3), тогда

()

или в матричной форме

, (17)

где — матрица, называемая фундаментальной матрицей системы уравнений (3). Определитель фундаментальной матрицы есть определитель Вронского и поэтому отличен от нуля на отрезке : .

Будем искать решение системы уравнений (2) в виде

, (18) где .

Подставляя выражение (18) в (2), получим

. (19)

В силу (17) уравнение (19) примет вид

(20) Так как и матрица непрерывна на , то существует непрерывная на обратная матрица .

Умножая обе части уравнения (20) слева на , получим

,

( 21)

где — произвольный постоянный вектор. Подставляя найденное выражение (21) для в формулу (18), получим

(22) Формула (22) дает общее решение неоднородной системы уравнений (2). Решение задачи Коши для системы (2) задается формулой

.

Метод нахождения решения системы (2) называется методом вариации постоянных или методом неопределенных коэффициентов Лагранжа.

Практически удобно поступать следующим образом: Уравнение (20) в развернутом виде

представляет собой систему линейных уравнений относительно :

,

,

.

Решая эту систему относительно (), получим или

.

Подставляя найденные выражения для в (18) получим общее решение для системы (2).

1. , Рождественский дифференциальные уравнения и основы вариационного исчисления. – М.: Наука, с.

2. и др. Сборник задач по обыкновенным дифференциальным уравнениям: Учеб. пособие для втузов. – М.: Высш. шк., с.: ил.

3. , , Перестюк уравнения: примеры и задачи: Учеб. пособие. – М.: Высш. шк., с.: ил.

Структура общего решения системы уравнений

Однородная система линейных уравнений

всегда совместна, так как имеет тривиальное решение . Если ранг матрицы системы равен количеству неизвестных , то тривиальное решение единственное. Предположим, что . Тогда однородная система имеет бесконечно много решений. Заметим, что расширенная матрица однородной системы при элементарных преобразованиях строк приводится к упрощенному виду , т.е. . Поэтому из (5.11) получаем общее решение однородной системы уравнений :

Получим другую форму записи решений однородной системы, которая раскрывает структуру множества решений. Для этого подчеркнем следующие свойства.

Свойства решений однородной системы уравнений

1. Если столбцы — решения однородной системы уравнений, то любая их линейная комбинация также является решением однородной системы.

В самом деле, из равенств следует, что

т.е. линейная комбинация решений является решением однородной системы.

2. Если ранг матрицы однородной системы равен , то система имеет линейно независимых решений.

Действительно, по формулам (5.13) общего решения однородной системы найдем частных решений , придавая свободным переменным следующие стандартные наборы значений (всякий раз полагая, что одна из свободных переменных равна единице, а остальные — равны нулю):

которые линейно независимы. В самом деле, если из этих столбцов составить матрицу, то последние ее строк образуют единичную матрицу. Следовательно, минор, расположенный в последних строках не равен нулю (он равен единице), т.е. является базисным. Поэтому ранг матрицы будет равен . Значит, все столбцы этой матрицы линейно независимы (см. теорему 3.4).

Любая совокупность линейно независимых решений однородной системы называется фундаментальной системой (совокупностью) решений .

Заметим, что фундаментальная система решений определяется неоднозначно. Однородная система может иметь разные фундаментальные системы решений, состоящие из одного и того же количества линейно независимых решений.

Теорема 5.3 об общем решении однородной системы. Если — фундаментальная система решений однородной системы уравнений (5.4), то столбец

при любых значениях произвольных постоянных также является решением системы (5.4), и, наоборот, для каждого решения х этой системы найдутся такие значения произвольных постоянных , при которых это решение удовлетворяет равенству (5.14).

Прямое утверждение теоремы следует из свойства 1 решений однородной системы. Докажем обратное утверждение о том, что любое решение можно представить в виде (5.14). Для этого составим матрицу , приписав к столбцам фундаментальной системы решений столбец

Найдем ранг этой матрицы. Так как первые столбцов линейно независимы, то . Так как каждый из столбцов матрицы является решением системы , то по первой формуле из (5.13) получаем

Следовательно, первая строка матрицы является линейной комбинацией последних строк этой матрицы.

По второй формуле из (5.13) получим, что вторая строка матрицы является линейной комбинацией последних строк этой матрицы, и т.д. По r-й формуле из (5.13) получим, что r-я строка матрицы является линейной комбинацией последних строк этой матрицы. Значит, первые строк матрицы можно вычеркнуть и при этом ранг матрицы не изменится. Следовательно, , так как после вычеркивания в матрице будет всего строк. Таким образом, . Значит, есть базисный минор матрицы , который расположен в первых ее столбцах, а столбец не входит в этот базисный минор. Тогда по теореме о базисном миноре найдутся такие числа , что

Итак, обратное утверждение доказано.

Алгоритм решения однородной системы уравнений

1-5. Выполнить первые 5 пунктов алгоритма Гаусса. При этом не требуется выяснять совместность системы, так как любая однородная система имеет решение (пункт 3 метода Гаусса следует пропустить). Получить формулы (5.11) общего решения, которые для однородной системы будут иметь вид (5.13).

Если ранг матрицы системы равен числу неизвестных , то система имеет единственное тривиальное решение и процесс решения заканчивается.

Если ранг матрицы системы меньше числа неизвестных , то система имеет бесконечно много решений. Структуру множества решений находим в следующих пунктах алгоритма.

6. Найти фундаментальную систему решений однородной системы. Для этого подставить в (5.13) последовательно стандартных наборов значений свободных переменных, в которых все свободные переменные равны нулю, кроме одной, равной единице (см. свойство 2 решений однородной системы).

7. Записать общее решение однородной системы по формуле (5.14).

1. В пункте 6 алгоритма вместо стандартного набора значений свободных переменных можно использовать и другие наборы значений, лишь бы они обеспечивали линейную независимость получаемых частных решений однородной системы.

2. Матрица столбцы которой образуют фундаментальную систему решений однородной системы, называется фундаментальной. Используя фундаментальную матрицу, общее решение (5.14) однородной системы можно записать в виде

3. Если базисный минор матрицы расположен в левом верхнем углу (в первых строках и первых столбцах), то упрощенный вид расширенной матрицы (5.9) однородной системы можно представить в виде блочной матрицы

Тогда блочная матрица размеров является фундаментальной. В этом можно убедиться, используя стандартные наборы значений свободных переменных. Применение блочных матриц может служить вторым способом нахождения фундаментальной системы решений.

Пример 5.4. Найти фундаментальную систему решений и общее решение однородной системы

Решение. 1. Составляем расширенную матрицу системы

2-4. Используя элементарные преобразования над строками матрицы , приводим ее к ступенчатому, а затем и к упрощенному виду (см. решение примера 5.3):

Пункт 3 метода Гаусса пропускаем.

5. Переменные — базисные, а — свободные. Записываем формулу (5.13) общего решения однородной системы

6. Находим фундаментальную систему решений. Так как и , надо подобрать линейно независимых решения. Подставляем в систему стандартные наборы значений свободных переменных:

В результате получили фундаментальную систему решений

7. Записываем общее решение однородной системы по формуле (5.14):

Заметим, что фундаментальную систему решений можно получить, взяв иные наборы значений свободных переменных. Например, и . Тогда получим другую фундаментальную систему решений

Несмотря на различия, обе формулы задают одно и то же множество решений.

Структура общего решения неоднородной системы уравнений

Ранее была выведена формула (5.11) общего решения системы линейных уравнений. Получим другую форму записи, отражающую структуру множества решений.

Рассмотрим неоднородную систему и соответствующую ей однородную систему . Между решениями этих систем имеются связи, выражающиеся следующими свойствами.

Свойства решений неоднородной системы уравнений

1. Разность двух решений и неоднородной системы есть решение однородной системы.

Действительно, из равенств и следует, что .

2. Пусть — решение неоднородной системы. Тогда любое решение неоднородной системы можно представить в виде

В самом деле, для любого решения неоднородной системы разность по свойству 1 является решением однородной системы, т.е. — решение однородной системы.

Теорема 5.4 о структуре общего решения неоднородной системы.

Пусть — решение неоднородной системы, а — фундаментальная система решений соответствующей однородной системы уравнений. Тогда столбец

при любых значениях [i]произвольных постоянных является решением неоднородной системы, и, наоборот, для каждого решения этой системы найдутся такие значения произвольных постоянных , при которых это решение удовлетворяет равенству (5.15).[/i]

Говорят, что общее решение неоднородной системы есть сумма частного решения неоднородной системы и общего решения соответствующей однородной системы.

Доказательство теоремы вытекает из свойств 1, 2 и теоремы 5.3.

Алгоритм решения неоднородной системы уравнений

1-5. Выполнить первые 5 пунктов метода Гаусса решения системы уравнений и получить формулу общего решения неоднородной системы вида (5.11).

6. Найти частное решение неоднородной системы, положив в (5.11) все свободные переменные равными нулю.

7. Записав формулы (5.13) общего решения соответствующей однородной системы, составить фундаментальную систему ее решений. Для этого подставить в (5.13) последовательно стандартных наборов значений свободных переменных, в которых все переменные равны нулю, за исключением одной, равной единице.

8. Записать общее решение неоднородной системы по формуле (5.15).

1. Используя фундаментальную матрицу однородной системы , решение неоднородной системы можно представить в виде

2. Если базисный минор матрицы расположен в левом верхнем углу (в первых строках и первых столбцах), то упрощенный вид расширенной матрицы (5.9) неоднородной системы можно представить в виде блочной матрицы

Тогда блочная матрица оказывается фундаментальной (см. п.3 замечаний 5.3), а столбец является частным решением неоднородной системы (в этом можно убедиться, подставляя в (5.11) нулевой набор свободных переменных). Используя блочные матрицы, общее решение (5 15) неоднородной системы можно представить в виде

где — столбец произвольных постоянных. Полученную формулу можно считать вторым способом решения неоднородной системы.

Пример 5.5. Найти структуру (5.15) общего решения неоднородной системы

Решение. 1-5. Первые 5 пунктов метода Гаусса выполнены при решении примера 5.3, где получены формулы общего решения неоднородной системы:

Переменные — базисные, а — свободные.

6. Полагая , получаем частное решение неоднородной системы .

7. Находим фундаментальную систему решений однородной системы (см. пример 5.4):

8. Записываем по формуле (5.15) общее решение неоднородной системы

Искомая структура множества решений найдена.

Получим формулу общего решения вторым способом , используя п.2 замечаний 5.4. При решении примера 5.3 расширенная матрица системы была приведена к упрощенному виду. Разбиваем ее на блоки:

Записываем частное решение неоднородной системы

и составляем фундаментальную матрицу:

По формуле (5.16) получаем общее решение неоднородной системы, которое преобразуем к виду (5.15):

Структура общего решения линейной системы дифференциальных уравнений

ФУНДАМЕНТАЛЬНАЯ СИСТЕМА РЕШЕНИЙ ОДНОРОДНОГО ЛИНЕЙНОГО ОДУ

Высшая математика

Рассмотрим линейное однородное дифференциальное уравнение

Фундаментальной системой решений однородного линейного дифференциального уравнения называется упорядоченный набор из n линейно независимых решений уравнения.

Доказано, что у однородного линейного дифференциального уравнения с непрерывными коэффициентами существует фундаментальная система решений.

И пусть функции y ₁ ( x ), y ₂( x ). y _n( x ) — решения линейного однородного уравнения с начальными условиями: