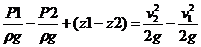Сумма m прихода сумма m расхода называется уравнением

5-я лекция, 2010 год.

5. КИНЕМАТИКА И ДИНАМИКА ЖИДКОСТИ

5.1. Основные понятия

5.2. Расход. Уравнение расхода

5.3. Уравнение Бернулли для элементарной струйки идеальной жидкости.

Три вида уравнения Бернулли для струйки идеальной жидкости.

5.1. Основные понятия

Кинематика жидкости существенно отличается от кинематики твердого тела. Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют; жидкость состоит из множества частиц движущихся одна относительно другой.

Скорость в данной точке пространства, занятого движущейся жидкостью, является функцией координат этой точки, а иногда и времени.

Задачей кинематики жидкости является определение скорости в любой точке жидкой среды, т. е. нахождение поля скоростей.

Мы сейчас рассмотрим движение идеальной жидкости, то есть жидкости, которая не обладает вязкостью.

В идеальной жидкости, так же как и в неподвижной реальной жидкости, возможен лишь один вид напряжений — нормальные напряжения сжатия, т. е. гидромеханическое давление.

Давление в движущейся идеальной жидкости обладает теми же свойствами, что и в неподвижной жидкости, на внешней поверхности жидкости оно направлено по нормали, а в любой точке внутри жидкости по всем направлениям одинаково.

Течение жидкости может быть установившимся или неустановившимся.

Установившимся называется течение жидкости, при котором давление и скорость являются функциями координат и не зависят от времени.

Давление и скорость могут измениться при перемещении частицы жидкости из одного положения в другое, но в данной неподвижной относительно русла точке давление и скорость при установившемся движении не изменяются во времени.

Последнее положение доказывается подобно тому, как это делалось для неподвижной жидкости (см. п. 1.4): составляются уравнения движения элементарного тетраэдра с учетом сил Д’Аламбера, которые затем вместе с массовыми силами стремятся к нулю при стягивании тетраэдра в точку.

р= f (х, у, z ); v = f ₂(х, у, z ); ,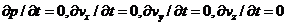

где индексы у скорости означают ее проекции на соответствующие оси, жестко связанные с руслом.

В частном случае установившееся течение может быть равномерным, когда скорость каждой частицы не изменяется с изменением ее координат и поле скоростей остается неизменным вдоль потока .

Примером установившегося течения может служить истечение жидкости из со суда, в котором поддерживается постоянный уровень, или движение жидкости в трубопроводе, создаваемое центробежным насосом с постоянной частотой вращения вала.

Неустановившимся называется течение жидкости, характеристики которого изменяются во времени в точках рассматриваемого пространства.

В общем случае при неустановившемся течении давление и скорость зависят как от координат, так и от времени:

Примерами неустановившегося течения жидкости могут служить быстрое опорожнение сосуда через отверстие в дне или движение во всасывающей или напорной трубе поршневого насоса, поршень которого совершает возвратно-поступательное движение.

Исследование установившихся течений гораздо проще, чем неустановившихся.

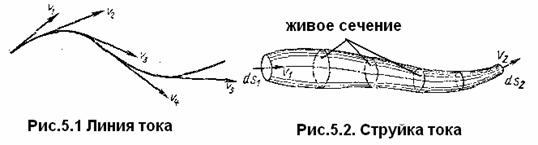
При установившемся течении траектории частиц жидкости являются неизменными по времени. При неустановившемся течении траектории различных частиц, проходящих через данную точку пространства, могут иметь разную форму. Поэтому для рассмотрения картины течения, возникающей в каждый данный момент времени, вводится понятие линии тока.

Линией тока называется кривая, в каждой точке которой вектор скорости в данный момент времени направлен по касательной к этой кривой (рис. 5.1).

Очевидно, что в условиях установившегося течения линия тока совпадает с траекторией частицы и не изменяет своей формы с течением времени.

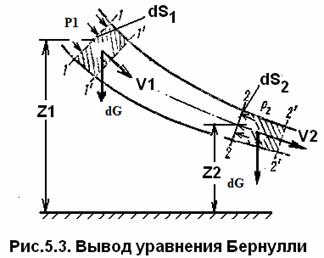
Трубкой тока называется бесконечно малый замкнутый контур, выделенный в данный момент времени в движущейся жидкости, через все точки которого проведены линии тока. Это условная трубчатая поверхность.

Элементарной струйкой называется часть потока, заключенная внутри трубки тока (рис.5.2).

В любой точке «трубки тока» т.е. на трубчатой поверхности струйки, векторы скорости направлены по касательной, а нормальные к этой поверхности составляющие скорости отсутствуют, следовательно, при установившемся движении ни одна частица жидкости, ни в одной точке трубки тока не может проникнуть внутрь струйки или выйти наружу.

Трубка тока, таким образом, является как бы непроницаемой стенкой, а элементарная струйка представляет собой самостоятельный элементарный поток.

Потоки конечных размеров будем сначала рассматривать, как совокупность элементарных струек, т. е. будем предполагать течение струйным. Из-за различия скоростей соседние струйки будут скользить одна по другой, но не будут перемешиваться одна с другой.

Живым сечением или сечением потока, называется площадь поверхности в пределах потока или струйки, проведенная нормально к линиям тока. Далее будем рассматривать в потоках такие участки, в которых струйки можно считать параллельными и, следовательно, живые сечения плоскими.

Различают напорные и безнапорные течения жидкости. Напорными называют течения в закрытых руслах без свободной поверхности, а безанапорными течения со свободной поверхностью. При напорных течениях давление вдоль потока обычно переменное, при безнапорном на свободной поверхности постоянное и чаще всего атмосферное. Примерами напорного течения могут служить течения в трубопроводах с повышенным (или пониженным) давлением, в гидромашинах или других гидроагрегатах. Безнапорными являются течения в реках, открытых каналах и лотках.

5.2. Расход. Уравнение расхода

Расходом называется количество жидкости, протекающее через живое сечение потока в единицу времени. Это количество можно измерить в единицах объема, в весовых единицах, в единицах массы в связи, с чем различают объемный Q , весовой Q_G и м ассовый расходы Q_m .

Для элементарной струйки, имеющей бесконечно малые площади сечений, можно считать истинную скорость одинаковой во всех точках каждого сечения. Следовательно, для этой струйки расходы равны.

объемный, (м 3 /с) dQ = v * dS , (5.136)

весовой, (Н/с) d Q_G = ρg * dQ , (5.2)

массовый, (кг/с) dQ_m = ρv * dS , (5.3)

где dS – площадь сечения струйки.

Для потока конечных размеров в общем случае скорость имеет различное значение в разных точках сечения, поэтому расход надо определять, как сумму элементарных расходов струек в данном сечении.

Q = 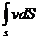. (5.4)

Обычно в рассмотрение вводят среднюю по сечению скорость v _ср = Q / S , откуда средний расход для струйки или потока равен

Условие неразрывности потока основывается на следующих свойствах, законе и предпосылках.

а) трубка тока имеет свойство непроницаемости для внешних, обтекающих ее потоков;

б) закон сохранения вещества;

в) предположение о сплошности (неразрывности) среды для установившегося течения несжимаемой жидкости.

На основании этих предпосылок и свойств можно утверждать, что объемный расход во всех сечениях элементарной струйки (см. рис.5.2) один и тот же

dQ = v ₁ * dS ₁ = v ₂ * dS ₂ → const (вдоль струйки). (5.6)
Это уравнение называется уравнением объемного расхода для элементарной струйки.

Аналогичное уравнение можно составить и для потока конечных размеров, ограниченного непроницаемыми стенками, только вместо истинных скоростей следует ввести средние скорости. В результате

Из последнего уравнения следует, что средние скорости в потоке несжимаемой жидкости обратно пропорциональны площадям сечений:

У равнение расхода (5.6‘) является следствием общего закона сохранения вещества для частных условий, в частности? для условий сплошности (неразрывности) течения.

5.3. Уравнение Бернулли для элементарной струйки

Рассмотрим установившееся течение идеальной жидкости находящейся под действием одной массовой силы — силы тяжести, и выведем для этого случая основное уравнение, связывающее между собой давление в жидкости и скорость ее движения.

Возьмем одну из элементарных струек, составляющих поток, выделим сечениями 1 и 2 участок этой струйки произвольной длины (рис.5.3). Пусть площадь первого сечения равна dS ₁ , скорость в нем V ₁ , давление P ₁ , а высота от произвольной плоскости сравнения Z ₁ . Во втором сечении dS ₂ , V ₂ , P ₂ и Z ₂ .

За бесконечно малый отрезок времени dt выделенный участок струйки переместится в положение 1’ – 2’ .

Применим к массе жидкости в объеме участка струйки теорему о кинетической энергии: работа сил, приложенных к телу, равна приращению кинетической энергии этого тела.

На жидкость действуют силы тяжести и силы давления, нормально к поверхности сечения рассматриваемого участка струйки.

Подсчитаем работу сил давления, сил тяжести и изменение кинетической энергии участка струйки за время dt . Эта теорема выглядит следующим образом.

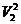
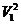
( m )/2 — ( m )/2 = G * h = G * (Z₁-Z₂)

Работа силы давления в первом сечении положительна, так как направление силы совпадает с направлением перемещения, и выражается как произведение силы p ₁* dS на путь V ₁ dt :

Работа силы давления во втором сечении имеет знак минус, так как направление силы прямо противоположно направлению перемещения, и определяется выражением

Силы давления, действующие по боковой поверхности отрезка струйки, работы не производят, так как они нормальны к этой поверхности и к перемещениям.

Работа сил давления равна

Работа силы тяжести равна изменению потенциальной энергии положения участка струйки, поэтому надо из потенциальной энергии жидкости в объеме 1 — 2 вычесть потенциальную энергию жидкости в объеме 1’- 2’ . При этом энергия промежуточного объема 1’- 2 сократится, и останется лишь разность энергии элементов 1- 1’ , 2- 2’ .

ПО уравнению расходов (закон сплошности среды) ( 5.6’ ) объемы и силы тяжести заштрихованных элементов 1 -1’ и 2 — 2’ равны между собой:

Тогда работа силы тяжести выразится как произведение разности высот на силу тяжести dG :

Чтобы подсчитать приращение кинетической энергии рассматриваемого участка струйки за время dt , необходимо из кинетической энергии объема 1’- 2’ вычесть кинетическую энергию объема 1 — 2. При вычитании кинетическая энергия промежуточного объема 1’ — 2 сократится, и останется лишь разность кинетических энергий элементов 2 — 2’ и 1 — 1’ , масса каждого из которых равна dG / g .

Таким образом, приращение кинетической энергии на участке струйки равно

Сложив работу сил давления (см. уравнение 5.7) с работой силы тяжести (5.9) и приравняв эту сумму приращению кинетической энергии (5.10), получим исходное уравнение для трех видов уравнения Бернулли.

Разделим это уравнение на dG (изменение силы тяжести элементарной струйки за время dt ) (см. формулу (5.8) , и произведя сокращения на

Сгруппируем члены, относящиеся к первому сечению, в левой части уравнения, а члены, относящиеся ко второму сечению, в правой:

( 5 . 12 )

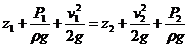
где z — геометрическая высота, или геометрический напор;

Р/ρ g – пьезометрическая высота или пьезометрический напор;

v 2 /2 g — скоростная высота или скоростной напор.

Полученное уравнение называется уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости. Оно было выведено Даниилом Бернулли в 1738 г .

Это уравнение является первой формой уравнения Бернулли, оно

( 5 . 13 )

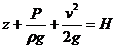
называется полным напором и имеет размерность длины.

Данное уравнение получено путем деления исходного уравнения (5.11), выражающего теорему об изменении кинетической энергии элементарной струйки, на ее изменении ее силы тяжести за время dt .

Уравнение Бернулли (5.13) записано для двух произвольно взятых сечении струйки и выражает равенство полных напоров Н в этих сечениях. Так как сечения взяты произвольно, следовательно, и для любого другого сечения этой же струйки полный напор будет иметь то же значение

(вдоль струйки)

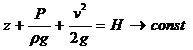
Для идеальной движущейся жидкости вдоль струйки тока сумма трех напоров: геометрического, пьезометрического и скоростного есть величина постоянная.

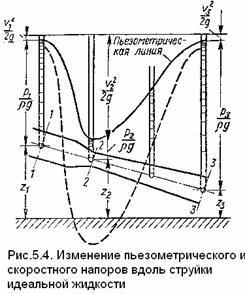
На рис. 5.4 показано изменение всех напоров вдоль струйки.

Линия изменения уровней жидкости в пьезометрах называется пьезометрической линией.

Из уравнения Бернулли и уравнения расхода следует, что если площадь поперечного сечения струйки уменьшается, т. е. струйка сужается, то скорость течения жидкости увеличивается, а давление уменьшается, и наоборот, если струйка расширяется, то скорость уменьшается, а давление возрастает.

На рис. 5.4 площадь поперечного сечения струйки от сечения 1 — 1 к сечению 2 — 2 уменьшается в 4 раза, скоростной напор увеличивается в 16 раз, а сечение 3 — 3 имеет ту же площадь, что и сечение 1-1.

Штриховой линией показано положение пьезометрической линия при тех же сечениях и при увеличении расхода в раз, вследствие чего скоростные высоты увеличиваются в 2 раза, а в узкой части струйки давление становятся меньше атмосферного.

Уравнение Бернулли можно записать в двух других формах. Разделив уравнение (5.11) на расход dQ = dS ₁* v ₁ dt = dS ₂* v ₂ dt , учитывая, что dG = ρ *g*dQ, а dQ = dG / ρ g, получим

, (5.15)

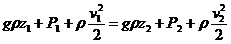
где все величины выражены в виде давлений.

В этой форме члены уравнения Бернулли имеют размерность давления и имеют следующие называния: ρ zg — весовое давление; р — гидромеханическое давление; ρ v 2 /2 — динамическое давление.

Разделив уравнение (5.11) на массу dm элементарного объема, равную ( ρ * v _1* dS ₁) * dt = ( ρ * v _2* dS ₂) * dt и преобразуем это уравнение подобно предыдущему. Тогда вместо выражения (5.15) будем иметь

(5.16)

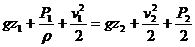
Введем понятие удельной энергии жидкости, в качестве которой рассмотрим отношение энергии к массе или объему.

Нетрудно показать, что члены уравнения (5.16) представляют собой различные формами удельной механической энергии, а именно:

gz — удельная потенциальная энергия (ее еще называют энергией положения), так как частица жидкости массой Δ m , находясь на высоте z , обладает энергией равной Δ mgz , а на единицу массы приходится энергия g Δ mz /Δ m = gz ;

р/ρ — удельная энергия давления (движущейся) жидкости, так как частица массой Δ m при давлении р обладает способностью подняться на высоту h = р/ρ g и приобрести, таким образом, энергию положения Δ mg р/(ρ g ) = р/ρ (после деления на Δ m получаем р/ρ);

сумма gz + р/ρ – удельная потенциальная энергия жидкости;

v 2 /2 — удельная кинетическая энергия жидкости, так как для той же частицы Δ m кинетическая энергия отнесенная к ее массе Δ m v 2 /2 : Δ m = v 2 /2;

Hg = zg + p /ρ+ v 2 /2 – полная удельная механическая энергия движущейся жидкости.

Таким образом, энергетический смысл уравнения Бернулли для элементарной струйки идеальной жидкости заключается в постоянстве вдоль струйки полной удельной энергии жидкости.

Механическая энергия жидкости может иметь три формы: потенциальная энергия, энергия давленияи и кинетическая энергия.

Первая и третья формы механической энергии известны из механики, они свойственны твердым и жидким телам.

Энергия давления является специфической для движущихся жидкостей. В процессе движения идеальной жидкости одна форма энергии может превращаться в другую, однако полная удельная энергия идеальной жидкости при этом как следует из уравнения Бернулли, остается без изменений.

Энергию давления легко преобразовать в механическую работу. Простейшим устройством, с помощью которого осуществляют такое преобразование, является цилиндр с поршнем (рис. 5.5). Покажем, что при этом преобразовании каждая единица массы жидкости совершает работу, численно равную р/ρ.

Пусть площадь поршня равна s , его ход L , избыточное давление жидкости в левой полости цилиндра необходимое для преодоления силы F равно Р = F / S , избыточное давление по другую сторону поршня равно нулю. Преодолевая силу F при перемещении поршня из левого положения, давление совершает работу А = Р SL . Расход жидкости, которую необходимо подвести к цилиндру для совершения этой работы за время t , равен объему цилиндра, т. е. Q t = W = SL .Удельная работа, приходящаяся на 1 кг массы,

Расход. Уравнение расхода

Расход, Уравнение расхода. Поток-это количество жидкости, протекающей через живой поток (поток) в единицу времени. Это количество может быть измерено в единицах объема, в единицах веса или в единицах массы. И вес (и масса (?Стоимость T. So, в этом потоке объем (м * с), Вес(Н / С) и масса (кг / с) стоят =(1.36)с = п & е(?; (1.37） М? Т =1.38.

Для потока элементов с бесконечно малым поперечным сечением можно предположить, что истинная скорость V одинакова во всех точках в каждой секции. Людмила Фирмаль

Площадь поперечного сечения струйки. В случае конечномерных течений, в общем случае, расход должен определяться как сумма основных расходов струи, так как скорости имеют разные значения в разных точках поперечного сечения (1.39） Шесть Обычно учитывается средняя скорость поперечного сечения b cp -?/ * ?, Откуда? = 17 СР (1.40)）

Исходя из закона сохранения вещества, непрерывности вращения (непрерывности) и приведенных выше характеристик текущей трубки («непроницаемой»), как и для стационарного течения несжимаемой жидкости, объемное течение на всех сечениях элементарного потока (рис.1.21) точно такое же.： & (?)= 38 g = V?。33%= sop $ 4 (вдоль потока) (1.41） Это уравнение называется основным уравнением объемного течения струйки. Аналогичные уравнения могут быть также созданы для конечномерных потоков, окруженных непроницаемыми walls.

Уравнение течения является результатом действия общего закона сохранения материала при определенных условиях, в частности условиях непрерывности (непрерывности) течения. Людмила Фирмаль

Нужно вводить только среднюю скорость, а не истинную speed. As итог ^ = Ver18 =VCp ^ 5 ^ =сшв ^ (вдоль потока). <1.42） Последнее уравнение показывает, что средняя скорость течения несжимаемой жидкости обратно пропорциональна площади поперечного сечения. В ^ CP1 / ^ CP2 ^ 2 / ^ 1.

Смотрите также:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Основы гидравлики

Уравнение Бернулли — фундамент гидродинамики

Бернулли — вне всякого сомнения — имя, знакомое и специалистам, и обывателям, которые хоть немного интересуются науками. Этот человек оставил ослепительный след в истории познавания человечеством окружающего мира, как физик, механик, гидравлик и просто общепризнанный гений, Даниил Бернулли навсегда останется в памяти благодарных потомков за свои идеи и выводы, которые долгое время существования человечества были покрыты мраком неизведанного.
Открытия и законы, которыми Бернулли осветил путь к познанию истины, являются фундаментальными, и придали ощутимый импульс развитию многих естественных наук. К таковым относится и уравнение Бернулли в Гидравлике, которое он вывел почти три века назад. Данное уравнение является основополагающим законом этой сложной науки, объясняющим многие явления, описанные даже древними учеными, например, великим Архимедом.

Попробуем уяснить несложную суть закона Бернулли (чаще его называют уравнением Бернулли), описывающего поведение жидкости в той или иной ситуации.

Выделим в стационарно текущей идеальной жидкости трубку тока, которая ограничена сечениями S₁ и S₂ , (рис. 1) .
(Понятие идеальной жидкости абстрактно, как и понятие всего идеального. Идеальной считается жидкость, в которой нет сил внутреннего трения, т. е. трения между отдельными слоями и частицами подвижной жидкости).
Пусть в месте сечения S₁ скорость течения ν₁ , давление p₁ и высота, на которой это сечение расположено, h₁ . Аналогично, в месте сечения S₂ скорость течения ν₂ , давление p₂ и высота сечения h₂ .

За бесконечно малый отрезок времени Δt жидкость переместится от сечения S₁ к сечению S₁‘ , от S₂ к S₂‘ .

По закону сохранения энергии, изменение полной энергии E₂ — E₁ идеальной несжимаемой жидкости равно работе А внешних сил по перемещению массы m жидкости:

где E₁ и E₂ — полные энергии жидкости массой m в местах сечений S₁ и S₂ соответственно.

С другой стороны, А — это работа, которая совершается при перемещении всей жидкости, расположенной между сечениями S₁ и S₂ , за рассматриваемый малый отрезок времени Δt .
Чтобы перенести массу m от S₁ до S₁‘ жидкость должна переместиться на расстояние L₁ = ν₁Δt и от S₂ до S₂‘ — на расстояние L₂ = ν₂Δt . Отметим, что L₁ и L₂ настолько малы, что всем точкам объемов, закрашенных на рис. 1 , приписывают постоянные значения скорости ν , давления р и высоты h .
Следовательно,

где F₁ = p₁S₁ и F₂ = — p₂S₂ (сила отрицательна, так как направлена в сторону, противоположную течению жидкости; см. рис. 1).

Полные энергии E₁ и E₂ будут складываться из кинетической и потенциальной энергий массы m жидкости:

Подставляя (3) и (4) в (1) и приравнивая (1) и (2) , получим

Согласно уравнению неразрывности для несжимаемой жидкости, объем, занимаемый жидкостью, всегда остается постоянным, т. е.

Разделив выражение (5) на ΔV , получим

где ρ — плотность жидкости.

После некоторых преобразований эту формулу можно представить в другом виде:

Поскольку сечения выбирались произвольно, то в общем случае можно записать:

ρv 2 /2 +ρgh +p = const (6) .

Выражение (6) получено швейцарским физиком Д. Бернулли (опубликовано в 1738 г.) и называется уравнением Бернулли.

Даниил Бернулли (Daniel Bernoulli, 1700 — 1782), швейцарский физик, механик и математик, один из создателей кинетической теории газов, гидродинамики и математической физики. Академик и иностранный почётный член (1733) Петербургской академии наук, член Академий: Болонской (1724), Берлинской (1747), Парижской (1748), Лондонского королевского общества (1750).

Уравнение Бернулли по своей сути является интерпретацией закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Уравнение хорошо выполняется и для реальных жидкостей, для которых внутреннее трение не очень велико.

Величина р в формуле (6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела) , величина ρν 2 /2 — динамическим давлением, величина ρgh — гидростатическим давлением.

Статическое давление обусловлено взаимодействием поверхности жидкости с внешней средой и является составляющей внутренней энергии рассматриваемого элементарного объема жидкости (т. е. характеризуется взаимодействием внутренних частиц жидкости, вызванных внешним возмущением — давлением) , а гидростатическое – положением этого объема жидкости в пространстве (зависит от высоты над поверхностью Земли) .
Динамическое давление характеризует кинематическую составляющую энергии этого объема, поскольку зависит от скорости потока, в котором движется рассматриваемый элементарный объем жидкости.

Для горизонтальной трубки тока изменение потенциальной составляющей ρgh будет равно нулю (поскольку h2 – h1 = 0) , и выражение (6) примет упрощенный вид:

ρv 2 /2 + p = const (7) .

Выражение p + ρν 2 /2 называется полным давлением.

Таким образом, содержание уравнения Бернулли для элементарной струйки при установившемся движении можно сформулировать так: удельная механическая энергия при установившемся движении элементарной струйки идеальной жидкости, представляющая собой сумму удельной потенциальной энергии положения и давления и удельной кинетической энергии, есть величина постоянная.

Все члены уравнения Бернулли измеряются в линейных единицах.

В гидравлике широко применяют термин напор, под которым подразумевают механическую энергию жидкости, отнесенную к единице ее веса (удельную энергию потока или неподвижной жидкости) .
Величину v 2 /2g называют скоростным (кинетическим) напором, показывающим, на какую высоту может подняться движущаяся жидкость за счет ее кинетической энергии.
Величину h_п = p/ρg называют пьезометрическим напором, показывающим на какую высоту поднимается жидкость в пьезометре под действием оказываемого на нее давления.
Величину z называют геометрическим напором, характеризующим положение центра тяжести соответствующего сечения движущейся струйки над условно выбранной плоскостью сравнения.

Сумму геометрического и пьезометрического напоров называют потенциальным напором, а сумму потенциального и скоростного напора — полным напором.

На основании анализа уравнения Бернулли можно сделать вывод, что при прочих неизменных параметрах потока (жидкости или газа) величина давления в его сечениях обратно пропорциональна скорости, т. е. чем выше давление, тем меньше скорость, и наоборот.
Это явление используется во многих технических конструкциях и устройствах, например, в карбюраторе автомобильного двигателя (диффузор), в форме крыла самолета. Увеличение скорости воздушного потока в диффузоре карбюратора приводит к созданию разрежения, всасывающего бензин из поплавковой камеры, а специальная форма сечения самолетного крыла позволяет создавать на его нижней стороне зону повышенного давления, способствующего появлению подъемной силы.

Геометрическая интерпретация уравнения Бернулли

Поскольку напор измеряется в линейных величинах, можно дать графическую (геометрическую) интерпретацию уравнению Бернулли и его составляющим.

На графике (рис. 2) представлена горизонтальная плоскость сравнения 0-0 , относительно которой геометрический напор будет в каждом сечении равен вертикальной координате z центра тяжести сечения (линия геометрического напора проходит по оси струйки) .
Линия К-К , характеризующая потенциальный напор струйки, получена сложением геометрического и пьезометрического напора в соответствующих сечениях (т. е. разница координат точек линии К-К и соответствующих точек оси струйки характеризует пьезометрический напор в данном сечении) .
Полный напор характеризуется линией MN , которая параллельна плоскости сравнения О-О , свидетельствуя о постоянстве полного напора H’_e (удельной механической энергии) идеальной струйки в любом ее сечении.

При движении реальной жидкости, обладающей вязкостью, возникают силы трения между ограничивающими поток поверхностями и между слоями внутри самой жидкости. Для преодоления этих сил трения расходуется энергия, которая превращается в теплоту и рассеивается в дальнейшем движущейся жидкостью. По этой причине графическое изображение уравнения Бернулли для идеальной жидкости будет отличаться от аналогичного графика для реальной жидкости.
Если обозначить h_f потери напора (удельной энергии) струйки на участке длиной L , то уравнение Бернулли для реальной жидкости примет вид:

Для реальной жидкости полный напор вдоль струйки не постоянен, а убывает по направлению течения жидкости, т. е. его графическая интерпретация имеет вид не прямой линии, а некоторой кривой МЕ (рис. 3) . Заштрихованная область характеризует потери напора.

Падение напора на единице длины элементарной струйки, измеренной вдоль оси струйки, называют гидравлическим уклоном:

Гидравлический уклон положителен, если напорная линия снижается по течению жидкости, что всегда бывает при установившемся движении.

Для практического применения уравнения Бернулли необходимо распространить его на поток реальной жидкости:

где α₁ , α₂ — коэффициенты Кориолиса, учитывающие различие скоростей в разных точках сечения потока реальной жидкости.
На практике обычно принимают α₁ = α₂ = α : для ламинарного режима течения жидкости в круглых трубах α = 2, для турбулентного режима α = 1,04. 1,1.

Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности ( S₁v₁Δt = S₂v₂Δt ) видно, что при течении жидкости по горизонтальной трубе, которая имеет различные сечения, скорость жидкости больше в более узких местах (где площадь сечения S меньше) , а статическое давление больше в более широких местах, т. е. там, где скорость меньше. Это можно увидеть, установив вдоль трубы ряд манометров.

Данный опыт показывает, что в манометрической трубке В , которая прикреплена к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С , которые прикреплены к широкой части трубы, что соответствует уравнению Бернулли.

Так как динамическое давление зависит от скорости движения жидкости (газа) , то уравнение Бернулли можно использовать для измерения скорости потока жидкости. Принципиально это свойство жидкости для определения скорости потока реализовано в так называемой трубке Пито – Прандтля (обычно ее называют трубкой Пито ) .

Трубка Пито – Прандтля ( см. рис. 2 ) состоит из двух тонких стеклянных трубок, одна из которых изогнута под прямым углом (Г-образно) , а вторая — прямая.
Одним из свободных концов каждая трубка присоединена к манометру.
Изогнутая трубка имеет открытый свободный конец, направленный против тока и принимающий напор потока жидкости, а вторая погружена в поток перпендикулярно току, и скорость потока на давление внутри трубки не влияет, т. е. внутри этой трубки действует лишь статическая составляющая давления жидкости.
Разница между давлением в первой трубке (полное давление) и второй трубке (статическое давление) , которую показывает манометр, является динамическим давлением, определяемым по формуле:

Определив с помощью трубки Пито — Прандтля динамическое давление в потоке жидкости, можно легко вычислить скорость этого потока:

Уравнение Бернулли также используют для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, с маленьким отверстием в боковой стенке на некоторой глубине ниже уровня жидкости.

Рассмотрим два сечения (на уровне h₁ свободной поверхности жидкости в сосуде и на уровне h₁ выхода ее из отверстия) и применим уравнение Бернулли:

Так как давления р₁ и р₂ в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. р₁ = р₂ , то уравнение будет иметь вид

Из уравнения неразрывности мы знаем, что ν₁/ν₂ = S₂/S₁ , где S₁ и S₂ — площади поперечных сечений сосуда и отверстия.
Если S₁ значительно превышает S₂ , то слагаемым ν₁ 2 /2 можно пренебречь и тогда:

Это выражение получило название формулы Торричелли.
Формулу Торричелли можно использовать для подсчета объемного (или массового) расхода жидкости, истекающего из отверстия в сосуде с поддерживаемым постоянно уровнем под действием атмосферного давления.
При этом используется формула Q = vS (для определения массового расхода – m = ρvS ) , по которой определяется расход жидкости за единицу времени.

Если требуется узнать расход жидкости за определенный промежуток времени t , то его определяют, умножив расход за единицу времени на время t .

Следует отметить, что такая методика расчета расхода реальной жидкости через отверстие в стенке сосуда дает некоторые погрешности, обусловленные физическими свойствами реальных жидкостей, поэтому требует применения поправочных коэффициентов (коэффициентов расхода) .

Пример решения задачи на определение расхода жидкости

Определить примерный объемный расход воды, истекающей из отверстия диаметром 10 мм, проделанном в вертикальной стенке широкого сосуда на высоте h = 1 м от верхнего, постоянно поддерживаемого, уровня воды за 10 секунд.
Ускорение свободного падения принять равным g = 10 м/с 2 .
Коэффициент расхода воды через отверстие — µ_s = 0,62.

По формуле Торричелли определим скорость истечения воды из отверстия:

v = √2gh = √2×10×1 ≈ 4,5 м/с.

Определим расход воды Q за время t = 10 секунд:

Q = µ_svSt = 0,62×4,5×3,14×0,012/4 × 10 ≈ 0,0022 м 3 ≈ 2,2 литра.

На практике расход жидкости в трубопроводах измеряют расходомерами, например, расходомером Вентури. Расходомер Вентури (см рис. 2) представляет собой конструкцию из двух конических патрубков, соединенных цилиндрическим патрубком. В сечениях основной трубы и цилиндрического патрубка устанавливают трубки-пьезометры, которые фиксируют уровень жидкости, обусловленный полным давлением в потоке.

При прохождении жидкости через сужающийся конический патрубок часть потенциальной энергии потока преобразуется в кинетическую, и, наоборот, – при прохождении потока по расширяющемуся коническому патрубку, кинетическая энергия уменьшается, а потенциальная растет. Это сказывается на скорости движения жидкости по рассматриваемым участкам. Перепад высоты уровня жидкости в пьезометрах позволяет рассчитать среднюю скорость потока жидкости на рассматриваемых участках и вычислить объемный расход по внутреннему сечению трубы.
В расходомерах учитываются потери напора в самом приборе при помощи коэффициента расхода прибора φ .

источники:

http://lfirmal.com/raskhod-uravnenie-raskhoda/

http://k-a-t.ru/gidravlika/7_Bernulli/

Сумма m прихода сумма m расхода называется уравнением