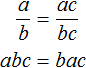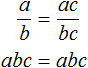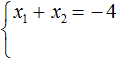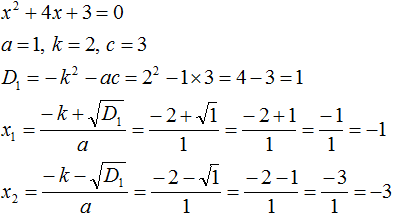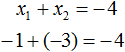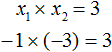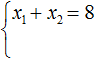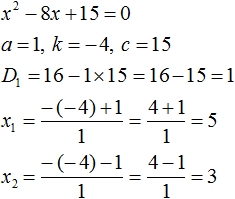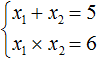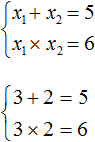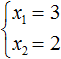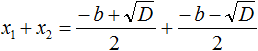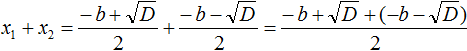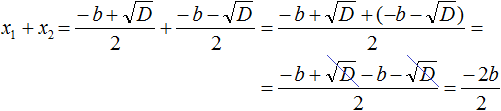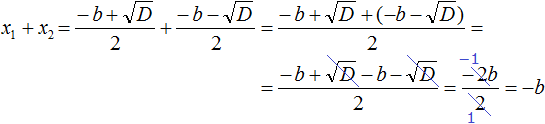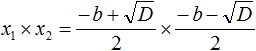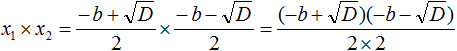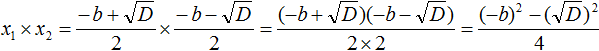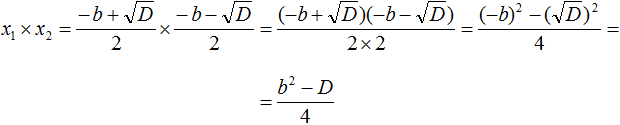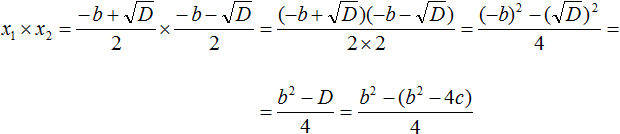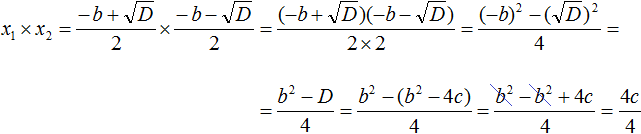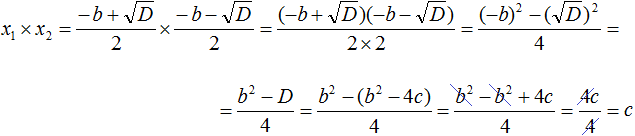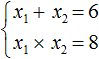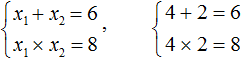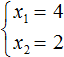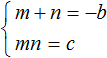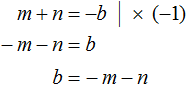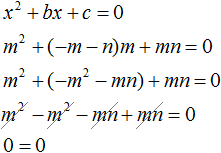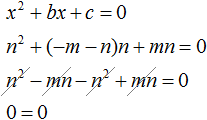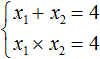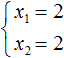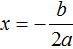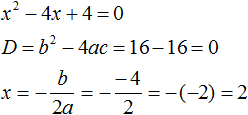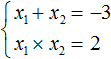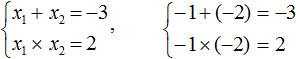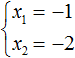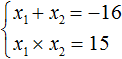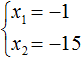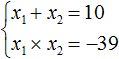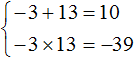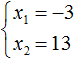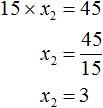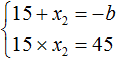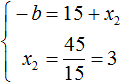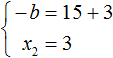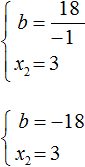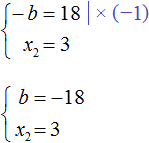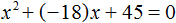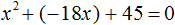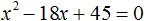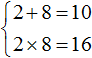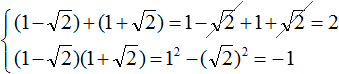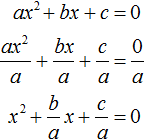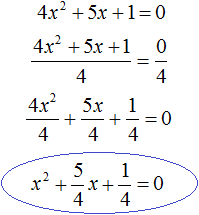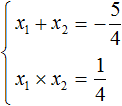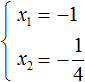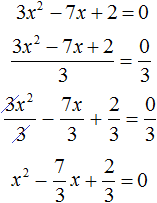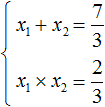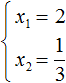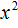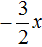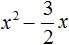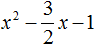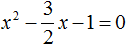Теорема Виета
Что называют теоремой?
Если человек обнаружил в математике какую-нибудь закономерность, позволяющую быстро решить ту или иную задачу, то ему не следует говорить о том, что он сделал открытие. Потому что может случиться так, что эта закономерность работает только для определённых случаев, а для других не работает или вовсе решает задачу неправильно.
Чтобы поделиться своим открытием с другими людьми, найденную закономерность следует сформулировать в виде утверждения, а затем доказать это утверждение, приводя неоспоримые факты.
Сформулированное утверждение называют теоремой. А доказательство теоремы состоит из фактов, логических рассуждений и вычислений, которые не оспариваются.
Например, теоремой можно назвать следующее утверждение:
«Если числитель и знаменатель обыкновенной дроби умнóжить на какое-нибудь число, то значение данной дроби не измéнится».
А затем привести такое доказательство:
Пусть, имеется дробь 
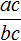

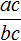
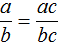
Для доказательства этого равенства воспользуемся основным свойством пропорции:
От перестановки мест сомножителей произведение не меняется. Поэтому в получившемся равенстве можно упорядочить правую часть по алфавиту:
Поскольку равенство 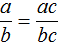

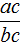
Теорема Виета
Французский математик Франсуа Виет выявил интересную взаимосвязь между коэффициентами приведённого квадратного уравнения и корнями этого же уравнения. Эта взаимосвязь представлена в виде теоремы и формулируется так:
Сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком, а произведение корней равно свободному члену.
То есть, если имеется приведённое квадратное уравнение x 2 + bx + c = 0 , а его корнями являются числа x1 и x2 , то справедливы следующие два равенства:
Знак системы (фигурная скобка) говорит о том, что значения x1 и x2 удовлетворяют обоим равенствам.
Покажем теорему Виета на примере приведённого квадратного уравнения x 2 + 4x + 3 = 0 .
Мы пока не знаем какие корни имеет уравнение x 2 + 4x + 3 = 0 . Но по теореме Виета можно записать, что сумма этих корней равна второму коэффициенту 4 , взятому с противоположным знáком. Если коэффициент 4 взять с противоположным знáком, то получим −4 . Тогда:
А произведение корней по теореме Виета будет равно свободному члену. В уравнении x 2 + 4x + 3 = 0 свободным членом является 3 . Тогда:
Теперь проверим действительно ли сумма корней равна −4 , и равно ли произведение 3 . Для этого найдём корни уравнения x 2 + 4x + 3 = 0 . А для удобства воспользуемся формулами для чётного второго коэффициента:
Корнями уравнения являются числа −1 и −3 . По теореме Виета их сумма должна была равняться второму коэффициенту уравнения x 2 + 4x + 3 = 0 , взятому с противоположным знаком. Действительно, так оно и есть. Вторым коэффициентов в уравнении x 2 + 4x + 3 = 0 является 4 . Если взять его с противоположным знаком и приравнять сумму корней x1 + x2 к этому коэффициенту, то получается верное равенство:
А произведение корней −1 и −3 по теореме Виета должно было равняться свободному члену уравнения x 2 + 4x + 3 = 0 , то есть числу 3 . Видим, что это условие тоже выполняется:
Значит выражение 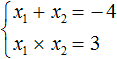
Рассмотрим квадратное уравнение x 2 − 8x + 15 = 0 . По теореме Виета сумма корней этого уравнения равна второму коэффициенту, взятому с противоположным знаком. Второй коэффициент равен −8 . Если взять его с противоположным знаком, то получим 8 . Тогда:
А произведение корней равно свободному члену. В уравнении x 2 − 8x + 15 = 0 свободным членом является 15 . Тогда:
Теперь проверим действительно ли сумма корней равна 8 , и равно ли произведение 15 . Для этого найдём корни данного уравнения. А для удобства воспользуемся формулами для чётного второго коэффициента. В этот раз пропустим нéкоторые подробные записи:
Видим, что корнями уравнения x 2 − 8x + 15 = 0 являются числа 5 и 3 . Их сумма равна 8 . То есть сумма корней равна второму коэффициенту уравнения x 2 − 8x + 15 = 0 , взятому с противоположным знаком.
А произведение чисел 5 и 3 равно 15 . То есть равно свободному члену уравнения x 2 − 8x + 15 = 0 .
Значит выражение 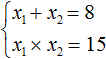
Замечание. Чтобы теорема Виета выполнялась, квадратное уравнение обязательно должно быть приведённым и иметь корни.
Например, рассмотрим квадратное уравнение x 2 − 2x + 4 = 0 . Напишем сумму и произведение корней этого уравнения:
Но уравнение x 2 − 2x + 4 = 0 не имеет корней, сумма которых равна 2, а произведение которых равно 4 . Убедиться в этом можно, вычислив дискриминант:
А значит записывать выражение 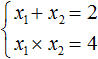
Теорема Виета полезна тем, что позволяет до начала решения узнать знаки корней уравнения.
Например, запишем для уравнения x 2 − 5x + 6 = 0 сумму и произведение его корней. Сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
Посмотрев на эти два равенства можно сразу понять, что оба корня должны быть положительными. Потому что произведение x1 × x2 = 6 будет выполняться только в двух случаях: если значения x1 и x2 положительны либо они оба отрицательны. Если эти значения будут отрицательными, то не будет выполняться равенство x1 + x2 = 5 , поскольку его правая часть равна положительному числу. А значения x1 и x2 должны удовлетворять как равенству x1 + x2 = 5 , так и равенству x1 × x2 = 6.
Ещё одна польза от теоремы Виета в том, что корни можно найти методом подбора. В данном примере корни должны быть такими, чтобы они удовлетворяли как равенству x1 + x2 = 5 так и равенству x1 × x2 = 6 . Очевидно, что таковыми являются корни 3 и 2
Доказательство теоремы Виета
Пусть дано приведённое квадратное уравнение x 2 + bx + c = 0 . Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
Вспомним формулы корней квадратного уравнения:
Найдём сумму корней x1 и x2 . Для этого подставим в выражение x1 + x2 вместо x1 и x2 соответствующие выражения из правой части формул корней квадратного уравнения. Не забываем, что в приведённом квадратном уравнении x 2 + bx + c = 0 старший коэффициент a равен единице. Тогда в процессе подстановки знаменатель станет равен просто 2
Запишем правую часть в виде дроби с одним знаменателем:
Раскроем скобки в числителе и приведём подобные члены:
Сократим дробь 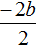
Теперь аналогично докажем, что произведение x1 × x2 равно свободному члену c .
Подставим вместо x1 и x2 соответствующие выражения из формул корней квадратного уравнения. Не забываем, что коэффициент a всё ещё равен единице:
Чтобы перемнóжить дроби, нужно перемнóжить их числители и знаменатели:
В числителе теперь содержится произведение суммы двух выражений и разности этих же выражений. Воспользуемся тождеством (a + b)(a − b) = a 2 − b 2 . Тогда в числителе полýчится 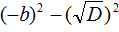
Теперь в числителе выражение (−b) 2 станет равно b 2 , а выражение 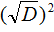
Но D равно b 2 − 4ac . Подстáвим это выражение вместо D , не забывая что a = 1 . То есть вместо b 2 − 4ac надо подставить b 2 − 4c
В получившемся выражении раскроем скобки в числителе и приведём подобные члены:
Сократим получившуюся дробь на 4
Таким образом, сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком ( x1 + x2 = −b ), а произведение корней равно свободному члену ( x1 × x2 = c ). Теорема доказана.
Теорема, обратная теореме Виета
Когда записана сумма и произведение корней приведённого квадратного уравнения, обычно начинается подбор подходящих корней к этому уравнению. В этот момент в работу включается так называемая теорема, обратная теореме Виета. Она формулируется так:
Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел x1 и x2 равно свободному члену уравнения x 2 + bx + c = 0, то числа x1 и x2 являются корнями уравнения x 2 + bx + c = 0.
Обратные теоремы бывают поставлены так, что их утверждением является заключение первой теоремы.
Так, доказывая теорему Виета мы пришли к заключению, что сумма x1 и x2 равна −b , а произведение x1 и x2 равно c . В обратной же теореме это заключение служит утверждением.
Ранее мы решили уравнение x 2 − 5x + 6 = 0 и написали для него такую сумму и произведение корней:
А затем подобрали корни 3 и 2 . По сути мы применили теорему, обратную теореме Виета. Числа 3 и 2 таковы, что их сумма равна второму коэффициенту уравнения x 2 − 5x + 6 = 0 , взятому с противоположным знаком (числу 5 ), а произведение чисел 3 и 2 равно свободному члену (числу 6 ). Значит числа 3 и 2 являются корнями уравнения x 2 − 5x + 6 = 0 .
Пример 2. Решить квадратное уравнение x 2 − 6x + 8 = 0 по теореме, обратной теореме Виета.
В данном уравнении a = 1 . Значит квадратное уравнение является приведённым. Его можно решить по теореме, обратной теореме Виета.
Сначала запишем сумму и произведение корней уравнения. Сумма корней будет равна 6 , поскольку второй коэффициент исходного уравнения равен −6 . А произведение корней будет равно 8
Теперь имея эти два равенства можно подобрать подходящие корни. Они должны удовлетворять как равенству x1 + x2 = 6 , так и равенству x1 × x2 = 8
Подбор корней удобнее выполнять с помощью их произведения. Используя равенство x1 × x2 = 8 нужно найти такие x1 и x2 , произведение которых равно 8.
Число 8 можно получить если перемножить числа 4 и 2 либо 1 и 8.
4 × 2 = 8
1 × 8 = 8
Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли не только равенству x1 × x2 = 8 , но и равенству x1 + x2 = 6 .
Сразу делаем вывод, что значения 1 и 8 не годятся, поскольку они хоть и удовлетворяют равенству x1 × x2 = 8 , но не удовлетворяют равенству x1 + x2 = 6 .
Зато значения 4 и 2 подходят как равенству x1 × x2 = 8 , так и равенству x1 + x2 = 6 , поскольку эти значения удовлетворяют обоим равенствам:
Значит корнями уравнения x 2 − 6x + 8 = 0 являются числа 4 и 2 .
Обратная теорема, как и любая теорема нуждается в доказательстве. Докажем теорему, обратную теореме Виета. Для удобства корни x1 и x2 обозначим как m и n . Тогда утверждение теоремы, обратной теореме Виета примет следующий вид:
Если числа m и n таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел m и n равно свободному члену уравнения x 2 + bx + c = 0, то числа m и n являются корнями уравнения x 2 + bx + c = 0
Для начала запишем, что сумма m и n равна −b , а произведение mn равно c
Чтобы доказать, что числа m и n являются корнями уравнения x 2 + bx + c = 0 , нужно поочередно подстáвить буквы m и n в это уравнение вместо x , затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями уравнения x 2 + bx + c = 0 .
Помимо букв m и n нам нужно знать чему равен параметр b . Выразим его из равенства m + n = −b . Легче всего это сделать, умножив обе части этого равенства на −1
Теперь всё готово для подстановок. Подстáвим m в уравнение x 2 + bx + c = 0 вместо x , а выражение −m − n подставим вместо b
Видим, что при x = m получается верное равенство. Значит число m является корнем уравнения x 2 + bx + c = 0 .
Аналогично докажем, что число n является корнем уравнения x 2 + bx + c = 0 . Подставим вместо x букву n , а вместо c подставим mn , поскольку c = mn .
Видим, что при x = n тоже получается верное равенство. Значит число n является корнем уравнения.
Следовательно, числа m и n являются корнями уравнения x 2 + bx + c = 0 .
Примеры решения уравнений по теореме, обратной теореме Виета
Пример 1. Решить квадратное уравнение x 2 − 4x + 4 = 0 по теореме, обратной теореме Виета.
Запишем сумму корней x1 и x2 и приравняем её к второму коэффициенту, взятому с противоположным знаком. Также запишем произведение корней x1 и x2 и приравняем его к свободному члену :
В данном примере очевидно, что корнями являются числа 2 и 2 . Потому что их сумма равна 4 и произведение равно 4
Значение x1 совпадает с x2 . Это тот случай, когда квадратное уравнение имеет только один корень. Если мы попробуем решить данное уравнение с помощью формул корней квадратного уравнения, то обнаружим что дискриминант равен нулю, и корень вычисляется по формуле
Данный пример показывает, что теорема обратная теореме Виета, работает и для уравнений, имеющих только один корень. Признаком того, что квадратное уравнение имеет только один корень является то, что значения x1 и x2 совпадают.
Пример 2. Решить уравнение x 2 + 3x + 2 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Теперь подберём значения x1 и x2 . Здесь начинается самое интересное. Произведение корней равно 2 . Число 2 можно получить перемножив 1 и 2 . Но сумма корней x1 + x2 равна отрицательному числу −3 . Значит значения 1 и 2 не подходят.
Сумма бывает отрицательной если оба слагаемых отрицательны либо отрицательным является одно слагаемое, модуль которого больше.
Если подберём корни с разными знаками, то не будет выполняться равенство x1 × x2 = 2 .
Если подберем положительные корни, то будет выполняться равенство x1 × x2 = 2 , но не будет выполняться равенство x1 + x2 = −3 .
Очевидно, что корнями являются два отрицательных числа. Произведение отрицательных чисел есть положительное число. А сумма отрицательных чисел есть отрицательное число.
Тогда равенствам будут удовлетворять числа −1 и −2 .
Итак, корнями являются числа −1 и −2
Пример 3. Решить уравнение x 2 + 16x + 15 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Как и в прошлом примере сумма корней равна отрицательному числу, а произведение корней — положительному числу.
Произведение бывает положительным если оба сомножителя положительны либо оба сомножителя отрицательны. Первый вариант отпадает сразу, поскольку сумма корней равна отрицательному числу. Тогда получается, что оба корня будут отрицательными. Попробуем подобрать их.
Число 15 можно получить, если перемножить числа −1 и −15 или (−3) и (−5) . В данном случае подходит первый вариант, поскольку сумма чисел −1 и −15 равна −16 , а их произведение равно 15 . Значит корнями уравнения x 2 + 16x + 15 = 0 являются числа −1 и −15
Пример 4. Решить уравнение x 2 − 10x − 39 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Произведение корней равно отрицательному числу. Значит один из корней является отрицательным. Число −39 можно получить если перемножить числа −3 и 13 либо −13 и 3 . Из этих комбинаций больше годится комбинация −3 и 13 , поскольку при перемножении этих чисел получается −39 , а при сложении 10
Значит корнями уравнения x 2 − 10x − 39 = 0 являются числа −3 и 13
Пример 5. Первый корень уравнения x 2 + bx + 45 = 0 равен 15 . Найти второй корень этого уравнения, а также значение коэффициента b .
По теореме Виета произведение корней приведённого квадратного уравнения равно свободному члену. В данном случае это произведение равно 45
При этом один из корней уже известен — это корень 15 .
Тогда второй корень будет равен 3 , потому что число 45 получается, если 15 умножить на 3
Этот второй корень также можно было бы получить, выразив из равенства 15 × x2 = 45 переменную x2
Теперь определим значение коэффициента b . Для этого напишем сумму корней уравнения:
По теореме Виета сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней равна 18, а 18 это положительное число, то в самóм уравнении этот коэффициент будет отрицательным:
Обычно решение к такой задаче записывают так. Сначала записывают основную теорему Виета в виде суммы и произведения корней:
Затем в это выражение подставляют имеющиеся известные значения. В нашем случае известно, что первый корень равен 15 , а свободный член уравнения x 2 + bx + 45 = 0 равен 45
Из этой системы следует найти x2 и b . Выразим эти параметры:
Из этой системы мы видим, что x2 равно 3. Подставим его в первое равенство:
Теперь из первого равенства мы видим, что −b равно 18
Но нас интересует b , а не −b . Следует помнить, что −b это −1b . Чтобы найти b нужно 18 разделить на −1 . Тогда b станет равно −18
Этот же результат можно получить если в выражении 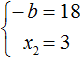
Теперь возвращаемся к исходному уравнению x 2 + bx + 45 = 0 и подставляем найденное значение b
Выполним умножение −18 на x . Получим −18x
Пример 6. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа 2 и 8 .
В этом задании корни уже известны. То есть x1 = 2 , x2 = 8 . По ним надо составить квадратное уравнение вида x 2 + bx + c = 0 .
Запишем сумму и произведение корней:
По теореме Виета сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней 2 и 8 равна 10 , то в самóм уравнении число 10 должно быть с противоположным знаком. Значит b = −10 .
Произведение корней по теореме Виета равно свободному члену. У нас это произведение равно 16 .
Значит b = −10 , c = 16 . Отсюда:
Пример 7. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа 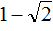
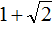
Запишем сумму и произведение корней:
Сумма корней равна 2. Тогда в уравнении второй коэффициент будет равен −2. А произведение корней равно −1. Значит свободный член будет равен −1. Тогда:
Когда квадратное уравнение неприведённое
Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым.
Если квадратное уравнение не является приведённым, но всё равно возникла необходимость применить теорему Виета, то обе части неприведённого квадратного уравнения следует разделить на коэффициент, который располагается перед x 2 .
Если к примеру в квадратном уравнении a x 2 + bx + c = 0 коэффициент a не равен единице, то данное уравнение является неприведённым. Чтобы сделать его приведённым, надо разделить обе его части на коэффициент, который располагается перед x 2 , то есть на a
Получилось уравнение 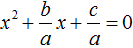


Например, решим квадратное уравнение 4x 2 + 5x + 1 = 0 . Это уравнение не является приведённым. Приведённым оно станет, если разделить обе его части на коэффициент, который располагается перед x 2 , то есть на 4
Получили приведённое квадратное уравнение. В нём второй коэффициент равен 

Отсюда методом подбора находим корни −1 и
Возможно этот метод вы редко будете использовать при решении квадратных уравнений. Но знать о нём не помешает.
Пример 2. Решить квадратное уравнение 3x 2 − 7x + 2 = 0
Данное уравнение не является приведённым, а значит его пока нельзя решить по теореме, обратной теореме Виета.
Сделаем данное уравнение приведенным. Разделим обе части на коэффициент, который располагается перед x 2
Получили уравнение 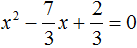
Отсюда методом подбора находим корни 2 и
Пример 3. Решить квадратное уравнение 2x 2 − 3x − 2 = 0
Это неприведённое квадратное уравнение. Чтобы сделать его приведённым, нужно разделить обе его части на 2 . Сделать это можно в уме. Если 2x 2 разделить на 2 , то полýчится x 2
Далее если −3x разделить на 2 , то полýчится 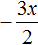
Далее если −2 разделить на 2 , то полýчится −1
Прирáвниваем получившееся выражение к нулю:
Теперь применяем теорему Виета. Сумма корней будет равна второму коэффициенту, взятому с противоположным знáком, а произведение корней свободному члену:
Отсюда методом подбора находим корни 2 и
Квадратное уравнение. Дискриминант. Теорема Виета.
теория по математике 📈 уравнения
Уравнение вида ax 2 +bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.
Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.
Дискриминант
Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).
Нахождение корней квадратного уравнения
Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:
D=b 2 –4ac
- Если D>0, то уравнение имеет два различных
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Пример №1. Решить уравнение х 2 –2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b 2 –4ac=(–2) 2 –41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:

D=b 2 –4ac=(–6) 2 –4=36–36=0, D=0, 1
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Теорема Виета
Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.
Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.
Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.
Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.
Пример №4. Решить уравнение х 2 –10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:
Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.
Пример №5. Решить уравнение: х 2 +5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:
Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:
Данное уравнение является квадратным. Но в его условии присутствует квадратный
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Решаем полученное неравенство: − х ≥ − 5 , отсюда х ≤ 5 . Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.
Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):
х 2 − 2 х + √ 5 − х − √ 5 − х − 24 = 0
Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:
х 2 − 2 х − 24 = 0
Итак, корнями уравнения х 2 − 2 х − 24 = 0 будут числа -4 и 6.
Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 н е ≤ 5 , а число минус 4 записываем в ответ нашего уравнения, так как − 4 ≤ 5 .
pазбирался: Даниил Романович | обсудить разбор | оценить
Квадратное уравнение. Парабола
Квадратичная функция
$s=\frac
В общем виде эту зависимость можно записать так: $y=ax^2$. График этой функции — парабола, вершина которой находится в точке (0,0). Ветви направлены вверх. Четная функция.
Квадратичной называется функция, которую можно задать формулой y=ax² + bx + c, причем а отлично от 0. Здесь a,b,c — некоторые числа, x — переменная.
Корень — это значение переменной, обращающее квадратный трёхчлен в ноль, а квадратное уравнение в верное равенство.
Vertex form
Можно выделить квадратный двучлен, поэтому это тоже парабола со сдвигом и растяжением.
Вершина параболы в точке (m,n), $m = \frac<-b><2a>, n = \frac<-D><4a>$
Квадратное уравнение
a — первый или старший коэффициент
b — второй коэффициент или средний или коэффициент при x
c — свободный член
Дискриминант $D = b^2-4ac$
Схематическое расположение параболы в зависимости от знаков первого коэффициента и дискриминанта.
Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент.
Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.
Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов кроме старшего (либо второй коэффициент, либо свободный член) равен нулю.
Теорема Виета
Теорема. Cумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Если приведенное квадратное уравнение $x^2 + px + q = 0$ имеет действительные корни, то их сумма равна $-p$, а произведение равно $q$, то есть
$$x_1 + x_2 = –p, \\ x_1 \cdot x_2 = q$$
Примечание. Любое квадратное уравнение можно привести к такому виду делением на a.
Пример. Найти сумму корней уравнения $x^2-7x+13=0$. Корней нет, поэтому ответ «сумма корней равна 7» — неверный. Для определения количества корней необходимо найти дискриминант.
Таким образом, в формулировку теоремы Виета необходимо добавить условие: если корни существуют, то … Или если дискриминант неотрицателен. Заметим, что при нулевом дискриминанте теорема Виета тоже работает (считать, что уравнение имеет два равных корня).
Пример. (Мерзляк, Алгебра 8 углубл, 2016)
Применения теоремы Виета
Теорема Виета позволяет угадывать целые корни квадратного трехчлена (не решая уравнение).
Так, находя корни квадратного уравнения x² – 5x + 6 = 0, можно начать с того, чтобы попытаться разложить свободный член (число 6) на два множителя так, чтобы их сумма равнялась бы числу 5. Это разложение очевидно: $$6 = 2 \cdot 3, \, 2 + 3 = 5. $$
Отсюда должно следовать, что числа 2 и 3 являются искомыми корнями.
Определение знаков корней
Определение знаков корней без решения уравнения (при условии что D > 0).
| p > 0 | p 0 | Корни имеют одинаковые знаки | |
|---|---|---|---|
| оба корня отрицательны | оба корня положительны | ||
| Свободный член q 0 | |||
Геометрический смысл теоремы Виета
Мы привыкли произносить «икс квадрат», «квадрат суммы», «удвоенный квадрат», не придавая этим выражениям геометрического смысла. На самом деле все они отражают взгляд на алгебру, который сложился еще в глубокой древности, потому что людям приходилось решать геометрические задачи на вычисление площадей.
В клинописных текстах древнего Вавилона (около 2000 лет до нашей эры) обнаружена такая задача. «Площадь 1000 состоит из суммы двух квадратов, и сторона меньшего составляет две трети стороны другого, уменьшенные на 10. Какова сторона бóльшего квадрата?»
Решить такую задачу — это все равно, что решить уравнение $x^2+(\frac 2 3 x-10)^2=1000$. В клинописном тексте нет формулы для решения этого уравнения, но перечисляются необходимые этапы вычисления, которые приводят к корню $x = 30$.
Фактически вавилонский метод дает решение системы $\begin
которая представляет собой запись задачи нахождения сторон прямоугольника с данным периметром и площадью. Теорема Виета, с изучения которой начинается этот параграф, связывает решение этой системы с решением квадратного уравнения.
Обобщение теоремы Виета
Теорема Вієта для зведеного многочлена $f(x)=x^n+a_
$$ x_1+x_2+\ldots+x_n=-a_
Разность корней квадратного уравнения
Для приведенного уравнения $$ x_1-x_2 = \sqrt
$$ <(x_1-x_2)^2>= x_1^2 — 2x_1x_2 + x_2^2 = (x_1+x_2)^2-4x_1x_2$$
Для приведенного уравнения с учетом теоремы Виета:
$$(x_1-x_2)^2 = (-b)^2-4c = b^2-4ac = D$$
Таким образом, если корни квадратного уравнения существуют, то расстояние между ними равно корню из дискриминанта. Грубо говоря, чем больше дискриминант, тем больше расстояние между корнями.
Обобщение дискриминанта
Дискриминантом многочлена $p(x)$ называется функция, задаваемая его коэффициентами.
Если точнее, то дискриминант — это произведение квадратов разностей корней многочлена, умноженное на старший коэффициент в степени на 2 меньше удвоенной степени многочлена.
1. Любая точка параболы равноудалена от некоторый точки, называемой фокусом параболы, и некоторой прямой, называемой ее директрисой.
2. Если вращать параболу вокруг ее оси симметрии (например, параболу $y = x^2$ вокруг оси Oy), то получается очень интересная поверхность, которая называется параболоидом вращения.
Поверхность жидкости, вращающейся в сосуде, имеет форму параболоида вращения. Вы можете увидеть эту поверхность, если помешаете ложечкой в неполном стакане чая, а потом вынете ложечку.
3. Если в пустоте бросить камень под некоторым углом к горизонту, то он полетит по параболе.
4. Если пересечь поверхность конуса плоскостью, параллельной какой-либо одной его образующей, то в сечении получится парабола.
5. В парках культуры устраивают иногда забавный аттракцион «Параболоид чудес». Каждому из стоящих внутри вращающегося параболоида кажется, что он стоит на полу, а остальные люди каким-то чудом держатся на стенках.
6. В зеркальных телескопах тоже применяют параболические зеркала: свет от далекой звезды, идущий параллельным пучком, упав на зеркало телескопа, собирается в фокусе.
7. У прожекторов зеркало обычно делается в форме параболоида. Если поместить источник света в фокусе параболоида, то лучи света, отразившись от параболического зеркала, образуют параллельный пучок.
Опыты, описанные в пунктах 2 и 5, основаны на одном и том же свойстве параболоида: если вращать параболоид с подходящей скоростью вокруг его оси, расположенной вертикально, то равнодействующая центробежной силы и силы тяготения в любой точке параболоида направлена перпендикулярно к его поверхности.
Солнечные концентраторы
Солнечные концентраторы используют энергию солнечной радиации, которая попадает на параболическую поверхность зеркала, в фокусе которой обычно располагается трубка с циркурирующим по ней теплоносителем. Как правило в качестве теплоносителя выступает масло. Теплоноситель нагревает воду, которая испаряясь поступает в турбогенератор в виде пара.
Параболические концентраторы с двигателем Стирлинга представляют собой СЭС с параболическими концентраторами, которые фокусируются на двигатель Стирлинга. Такие электростанции характеризуются высоким КПД (более 31%). В качестве рабочего тела двигателя Стирлинга используется, как правило, водород, или гелий.
Согласно известной исторической легенде, Архимед почти полностью сжег флот римского полководца Марка Марцелла, используя медные параболические зеркала.
8-этажное сооружение, включающее около 10 тысяч отдельных параболических зеркал. На сегодняшний день Солнечная Печь, выстроенная в 1970 году в Восточных Пиренеях – крупнейшая в мире. Массив зеркал действует в качестве параболического отражателя. Свет фокусируется в одном центре. И температура там может достигать 3500 градусов по Цельсию. При такой температуре можно плавить сталь. Но температуру можно регулировать, устанавливая зеркала под разными углами.
Подвесные мосты
Вантовый мост — тип висячего моста, состоящий из одного или более пилонов, соединённых с дорожным полотном посредством прямолинейных стальных тросов — вантов. В отличие от висячих мостов, где дорожное полотно поддерживается вертикальными тросами, прикреплёнными к протянутым по всей длине моста основным несущим тросам, у вантовых мостов тросы (ванты) соединяются непосредственно с пилоном.
Русский мост (Владивосток) — вантовый мост с самым длинным основным пролётом в мире (1104 м), при общей длине в 1886 м
Висячий мост — мост, в котором основная несущая конструкция выполнена из гибких элементов (кабелей, канатов, цепей и др.), работающих на растяжение, а проезжая часть подвешена.
Висячие мосты находят наиболее удачное применение в случае большой длины моста, невозможности или опасности установки промежуточных опор (например в судоходных местах).

Золотые Ворота (Сан-Франциско) — один из самых узнаваемых мостов в мире. Мост был самым большим висячим мостом в мире с момента открытия в 1937 году и до 1964 года. Общая длина моста — 2737 м, длина основного пролёта — 1280 м, высота опор — 227 м над водой, масса — 894 500 т. В среднем, по мосту проезжают сто тысяч автомобилей в сутки. 6 полос.
Основные несущие тросы (или цепи) подвешивают между установленными по берегам пилонами. К этим тросам крепят вертикальные тросы или балки, на которых подвешивается дорожное полотно основного пролёта моста. Основные тросы продолжаются за пилонами и закрепляются на уровне земли. Продолжение тросов может использоваться для поддержки двух дополнительных пролётов.
Под действием сосредоточенной нагрузки несущая конструкция может изменять свою форму, что уменьшает жёсткость моста. Для избежания прогибов в современных висячих мостах дорожное полотно усиливают продольными балками или фермами, распределяющими нагрузку.
Используются также конструкции, в которых дорожное полотно поддерживается системой прямолинейных канатов, закреплённых непосредственно на пилонах. Такие мосты называются вантовыми.
Основной пролёт можно сделать очень длинным при минимальном количестве материала. Поэтому использование такой конструкции очень эффективно при строительстве мостов через широкие ущелья и водные преграды. В современных висячих мостах широко применяют проволочные тросы и канаты из высокопрочной стали с пределом прочности около 2—2,5 ГПа(200-250 кгс/мм²), что существенно снижает собственный вес моста.
Отсутствует необходимость ставить промежуточные опоры, что даёт большие преимущества, например, в случае горных разломов или рек с сильным течением.
Будучи относительно податливыми, висячие мосты могут, без ущерба для целостности конструкции, изгибаться под действием сильного ветра или сейсмических нагрузок, тогда как более жёсткие мосты нужно строить более крепкими и тяжёлыми.
Полотно моста сильно прогибается, если на одном участке сосредоточена нагрузка существенно больше, чем на других. Из-за этого висячие мосты реже используются в качестве железнодорожных, чем другие типы.
Основные напряжения в висячем мосте — это напряжения растяжения в основных тросах и напряжения сжатия в опорах, напряжения в самом пролёте малы. Почти все силы в опорах направлены вертикально вниз и стабилизируются за счёт тросов, поэтому опоры могут быть очень тонкими. Сравнительно простое распределение нагрузок по разным элементам конструкции упрощает расчёт висячих мостов.
Под действием собственного веса и веса мостового пролёта тросы провисают и образуют дугу, близкую к параболе. Ненагруженный трос, подвешенный между двумя опорами, принимает форму т. н. «цепной линии», которая близка к параболе в почти горизонтальном участке. Если весом тросов можно пренебречь, а вес пролёта равномерно распределён по длине моста, тросы принимают форму параболы. Если вес троса сравним с весом дорожного полотна, то его форма будет промежуточной между цепной линией и параболой.
Клифтонский мост близ Бристоля (инженер Изамбард Кингдом Брюнель, 1864).

Акаси-Кайкё — самый длинный подвесной мост в мире. Полная длина составляет 3911 м. Пилоны имеют высоту 298 м, что выше 90-этажного дома.
Вначале были построены два бетонных основания для пилонов на дне пролива Акаси. Для строительства этого моста был разработан специальный бетон, который не растворяется в воде при заливке. Следующим этапом было протягивание тросов. Для этого нужно было с одного пилона на другой протянуть направляющий канат. Он был протянут с помощью вертолёта. Когда в 1995 году оба троса были протянуты, и можно было приступать к монтажу дорожного полотна, произошло непредвиденное: город Кобе стал жертвой крупного землетрясения магнитудой в 7,3 балла. Пилоны выдержали землетрясение, но из-за изменения рельефа дна пролива один из пилонов сдвинулся на 1 м в сторону, таким образом нарушив все расчёты. Инженеры предложили удлинить балки дорожного полотна и увеличить расстояние между вантами, свисающими с основных тросов. Строительные работы, задержанные не более чем на месяц, возобновились. Монтаж дорожного полотна закончился в 1998 году.
В конструкции моста имеется система двухшарнирных балок жёсткости, позволяющая выдерживать скорости ветра до 80 м/с, землетрясения магнитудой до 8,5 и противостоять сильным морским течениям. Для уменьшения действующих на мост нагрузок имеется система динамических гасителей колебаний.
Если вытянуть в длину все стальные нити (диаметром 5,23 мм) несущих тросов моста Акаси-Кайкё, то ими можно опоясать земной шар более семи раз.
Модель параболы
Легко получить параболу с помощью обычного карманного фонарика. Световое пятно от вертикально расположенного фонаря будет кругом. Немного повернём его, и пятно будет иметь форму эллипса. При дальнейшем повороте фонарика эллипс будет всё больше и больше вытягиваться, а в некоторый момент его наиболее удалённая точка уйдёт в бесконечность. Кривая, ограничивающая такое пятно, называется параболой. Неограниченные кривые, которые получаются при дальнейшем вращении фонарика, называются гиперболами. Все получившиеся кривые – окружность, эллипс, парабола, гипербола – конические сечения. Такое название они получили заслуженно, поскольку световой столб, выходящий из фонарика, является конусом.
Парабола, как огибающая
Параболу можно рассматривать, как огибающую семейства прямых.
См. также Конические сечения — Параболическое зеркало. Параболический бильярд
Цепочки окружностей, вписанных в кривую 2-го порядка
Если радиус окружности, вписанной в параболу $y=x^2$ равен 1, то радиус второй окружности, вписанной в эту же параболу и касающейся первой окружности, равен 2, радиус аналогичной 3-й окружности равен 3 и т. д.
Интересно, что радиусы подобной цепочки окружностей, вписанных в угол, образуют геометрическую прогрессию.
Фокус и директриса параболы
Задача. Постройте график функции $y = x^2$. Масштаб возьмите покрупней: 1 = 4 клетки. Отметьте на оси Oy точку F(0; 1/4). Полоской бумаги измерьте расстояние от точки F до какой-нибудь точки M параболы. Затем приколите полоску в точке M и поверните ее вокруг этой точки так, чтобы она стала вертикальной. Конец полоски опустится немного ниже оси абсцисс. Отметьте на полоске, насколько она выйдет за ось абсцисс. Возьмите теперь другую точку на параболе и повторите измерение еще раз. Насколько теперь опустился край полоски за ось абсцисс?
Результат мы Вам сможем сказать заранее: какую бы точку на параболе вы ни взяли, расстояние от этой точки до точки (0; 1/4) будет больше расстояния от той же точки до оси абсцисс всегда на одно и то же число — на 1/4. Можно сказать иначе: расстояние от любой точки параболы $y = x^2$ до точки (0; 1/4) равно расстоянию от той же точки параболы до прямой y = −1/4, параллельной оси Ox.
Замечательная точка F(0; 1/4) называется фокусом параболы, а прямая y = −1/4 — директрисой (по-русски направляющая) этой параболы. Директриса и фокус есть у всякой параболы.
Геометрический смысл параболы
Парабола — это множество точек, равноудалённых от данной прямой (директрисы параболы) и не лежащей на директрисе данной точки (фокуса параболы).
Парабола — это множество центров окружностей, касающихся данного круга и данной прямой, касающейся этого круга.
Источник — подробнее, больше картинок
Задача. Свободно падающее тело
Тело, свободно падающее без начальной скорости с некоторой высоты, за последнюю секунду падения проходит путь в 7 раз больший чем за первую секунду движения. Найдите высоту, с которой падает тело.
За первую секунду тело пройдёт расстояние равное: $S=\frac
Тогда за последнюю секунду тело пройдёт расстояние равное 35 м. С другой стороны, за последнюю секунду тело пройдет расстояние: $$ \frac
Решив это уравнение получим t = 4 с, откуда S = 80 м
| t, с | 1 | 2 | 3 | 4 | 5 | 6 |
| s общий, м | 5 | 20 | 45 | 80 | 125 | 180 |
| s за последнюю секунду | 5 | 15=20-5 | 25=45-20 | 35=80-45 | 45=125-80 | 55 |
Таким образом, любое падающее тело за первую секунду проходит 5м, за вторую секунду — в 3 раза больше, за третью — в 5 раз больше, за четвертую — в 7 раз больший путь, за пятую — в 9 раз, за шестую — в 11 раз. Арифметическая прогрессия, физики называют это закон нечетных чисел. Путь, пройденный за секунду, тоже образует арифметическую прогрессию с разность 10, что соответствует ускорению свободного падения g.
Задача. Тело, падающее без начальной скорости, за последнюю секунду падения прошло путь s = 35 м. Какую скорость имело тело в момент падения на землю? Сопротивлением воздуха пренебречь.
Решение. Время падения = 4 с. Скорость $v = s’ = gt = 40$ м/с.
http://spadilo.ru/kvadratnoe-uravnenie-i-diskriminant/
http://xlench.bget.ru/doku.php/mat/algebra/sq-equ?do=export_xhtml