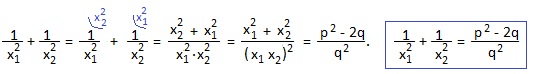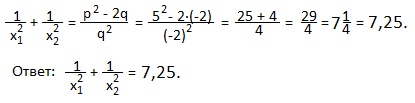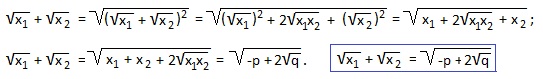Сумма обратных величин корней уравнения

Теорема Виета — ФОРМУЛА КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ — КВАДРАТНЫЕ УРАВНЕНИЯ

Цели: доказать прямую и обратную теоремы Виета, использовать их при решении задач.

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

1. Произведение двух последовательных натуральных нечетных чисел равно 575. Найти эти числа.

2. Найти стороны прямоугольника, если известно, что одна из них на 17 см больше другой, а диагональ прямоугольника равна 25 см.

1. Произведение двух последовательных натуральных четных чисел равно 624. Найти эти числа.

2. Найти катеты прямоугольного треугольника, если один из них на 7 см меньше другого, а гипотенуза равна 17 см.

III. Изучение нового материала (основные понятия)

1. Подход к формулировке прямой теоремы Виета

Сначала рассмотрим несколько приведенных квадратных уравнений. Найдем их корни, а также сумму и произведение этих корней.

Какие закономерности вы видите между суммой и произведением корней уравнения и его коэффициентами? Попробуйте их сформулировать.

Видно, что для каждого из приведенных уравнений сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену. Такое утверждение называется прямой теоремой Виета и выполняется для любого приведенного квадратного уравнения, имеющего корни. Докажем эту теорему.

2. Доказательство прямой теоремы Виета

Рассмотрим приведенное квадратное уравнение х2 + рх + q = 0 (где старший коэффициент равен 1, второй коэффициент обозначен буквой р, свободный член — буквой q). Найдем его дискриминант D= р2 – 4q. Пусть D ≥ 0, тогда уравнение имеет два различных (D > 0) или равных (D = 0) корня: Найдем сумму и произведение этих корней: и Итак, доказано, что х1 + х2 = -р и x1x2 = q.

Заметим, что и ранее и сейчас в случае, когда дискриминант квадратного уравнения равнялся нулю, мы говорили, что уравнение имеет два равных (или одинаковых) корня. Тогда теорема Виета выполняется. Если считать, что в этом случае уравнение имеет один корень, то непонятно, как использовать теорему Виета (что в этом случае считать корнем х2).

Теорему Виета легко обобщить на произвольное квадратное уравнение ax2 + bх + с = 0. Пусть это уравнение имеет корни х1 и х2. Разделим все части уравнения на старший коэффициент а и получим равносильное приведенное квадратное уравнение Для него (и для исходного уравнения) по доказанной теореме Виета выполняются соотношения:

3. Обратная теорема Виета

Если числа m и n таковы, что их сумма равна числу -р, а произведение равно числу q, то числа тип являются корнями приведенного квадратного уравнения x2 + px + q = 0. Докажем это утверждение.

По условию m + n = -р, а р = -(m + n) и mn = q. Подставим величины р и q в уравнение x2 + px + q = 0 и получим уравнение х2 — (m + n)х + mn = 0. Проверим, что число m является корнем этого уравнения. Подставим вместо х число m и получим: (верное равенство). Следовательно, число т является корнем уравнения x2 + px + q = 0. Аналогично доказывается, что число п также является корнем этого уравнения. Рассмотрим примеры применения прямой и обратной теорем Виета.

Пусть уравнение 3х2 — 7х + 1 = 0 имеет корни х1 и х2.

а) сумму корней х1 + х2;

б) произведение корней х1х2;

в) сумму обратных величин корней

г) сумму квадратов корней х12 + х22;

д) сумму кубов корней х13 + х23;

е) модуль разности корней |х1 — х2|.

Найдем дискриминант данного уравнения D = (-7)2 – 4 · 3 · 1 = 37. Так как D > 0, то уравнение имеет два различных корня. Так как дискриминант не является квадратом натурального числа, то корни уравнения х1 и х2 — иррациональные числа. Поэтому прямое и непосредственное вычисление пунктов а-е затруднительно. Следовательно, для вычислений используем прямую теорему Виета.

Разделим все члены данного уравнения на старший коэффициент 3 и получим равносильное уравнение Тогда по теореме Виета сразу получаем:

Для вычисления остальных пунктов надо выразить требуемые комбинации корней через их сумму и произведение.

в) Приведем дроби к общему знаменателю

г) Используем формулу квадрата суммы:

д) Применим формулу суммы кубов: Подставим в это выражение значения величин х1 + х2 и х1х2. Получаем:

е) Используем свойство арифметического корня и формулу квадрата разности: Подставим в это выражение значения величин х12 + х22 и х1х2 и получим:

Решим уравнение 197×2 — 2197х + 2000 = 0.

Очевидно, что вычисление дискриминанта этого уравнения D = (-2197)2 – 4 · 197 · 2000 достаточно трудоемко. Поэтому проще решить это уравнение подбором. Очевидно, что один корень уравнения х1 = 1. При подстановке этого значения в уравнение получаем 197 · 12 — 2197 · 1 + 2000 = 0 (верное равенство).

По прямой теореме Виета имеем откуда корень Используя обратную теорему Виета, проверим найденные корни. Сумма корней и произведение корней (это соотношение мы уже использовали). Поэтому числа х1 и х2 являются корнями уравнения

Умножим все члены на число 197 и получим равносильное уравнение 197×2 – 2197x + 2000 = 0. Таким образом, на основании обратной теоремы Виета мы показали, что числа х1 = 1 и являются корнями данного уравнения 197×2 — 2197х + 2000 = 0.

Напишем квадратное уравнение, корни которого х1 = -1/3 и х2 = 1/5.

Найдем сумму и произведение данных корней: и Тогда по обратной теореме Виета числа х1 и х2 являются корнями уравнения Умножим все члены на число 15 и получим равносильное уравнение 15х2 + 2х — 1 = 0, которое имеет заданные корни х1 и х2.

Не решая уравнения 7х2 + 18х + 3 = 0, определим знаки его корней.

Дискриминант этого уравнения D = 182 — 4 · 7 · 3 = 240. Так как D > 0, то данное уравнение имеет два различных корня. Определим знаки этих корней. Используя прямую теорему Виета, имеем: Так как х1х2 > 0, то числа х1 и х2 имеют одинаковые знаки (или оба положительные, или оба отрицательные). Так как при этом x1 + х2 0, то уравнение имеет различные корни х1 и х2. Сами корни х1 и х2 находить не будем, но найдем по прямой теореме Виета сумму и произведение этих корней:

В уравнении, которое надо написать, будем обозначать неизвестную буквой у. По условию корни этого уравнения удовлетворяют соотношениям у1 = 2х, и у2 = 2х2. Найдем сумму и произведение этих корней: и Тогда по обратной теореме Виета числа y1 и у2 являются корнями уравнения у2 + 4у + 12/7 = 0. Умножим все члены на число 7 и получим равносильное уравнение 7y2 + 28у + 12 = 0. Оно удовлетворяет условиям задачи.

Сравним данное уравнение 7х2 + 14х + 3 = 0 с корнями х1 и х2 и полученное уравнение 7у2 + 28у + 12 = 0 с корнями 2х1 и 2х2. Видно, что старшие коэффициенты в уравнениях одинаковы. Второй коэффициент полученного уравнения в 2 раза больше, чем у данного. Свободный член полученного уравнения в 22 = 4 раза больше, чем у данного.

Решите уравнение х2 — 4х + a = 0, если его корни х1 и х2 связаны равенством 2х1 + х2 = 3. Найдите значение параметра а.

Сначала найдем корни данного уравнения. Для этого используем прямую теорему Виета х1 + х2 = 4 и данное равенство 2х1 + х2 = 3. Решим систему линейных уравнений методом сложения. Вычтем из первого уравнения второе: 2х1 + х2 – х1 — х2 = 3 — 4 , откуда х1 = -1. Из второго уравнения находим х2 = 4 – х1 = 4 — (-1) = 5.

Теперь определим значение параметра а. Для этого еще раз используем прямую теорему Виета. Получаем а = x1x2 = -1 · 5 = -5. Итак, х1 = -1 и х2 = 5, а = -5.

При каком значении параметра а сумма корней уравнения имеет наименьшую величину? Найдите эту величину.

Найдем дискриминант данного уравнения Очевидно, что при любых значениях а дискриминант положительный. Поэтому уравнение имеет два различных корня х1 и х2. По прямой теореме Виета сумма этих корней х1 + х2 = а2 — 6а. Преобразуем это выражение, выделив квадрат двучлена: Видно, что сумма корней состоит из неотрицательного слагаемого (а — 3)2 и отрицательного числа -9. Поэтому она будет наименьшей, если слагаемое (a – 3)2 самое маленькое, т. е. (а — 3)2 = 0, откуда а = 3. Итак, при а = 3 сумма корней данного уравнения наименьшая и равна -9.

IV. Контрольные вопросы

1. Сформулируйте и докажите прямую теорему Виета для уравнения х2 + pх + q = 0.

2. Сформулируйте и докажите прямую теорему Виета для уравнения ах2 + bх + с = 0.

3. Сформулируйте и докажите обратную теорему Виета.

V. Задание на уроке

№ 573 (а, в, д); 574 (а, б); 576 (а); 578; 581; 583; 584 (а); 585 (а, в).

VI. Задание на дом

№ 573 (б, г, ж); 575 (а, д); 576 (в); 579; 580; 582; 584 (б); 586 (а, г).

VII. Творческие задания

1. Напишите квадратное уравнение, корни которого равны:

Ответы: а) 4х2 — 4х + 1 = 0; б) 9х2 + 6х + 1 = 0; в) 5х2 — 9х — 2 = 0; г) 4х2 + 11х — 3 = 0; д) 6х2 – х — 1 = 0; е) 10х2 + 3х — 1 = 0.

2. Квадратное уравнение 3х2 — 5х + 1 = 0 имеет корни х1 и х2. Напишите квадратное уравнение, корни которого равны:

Ответы: а) 3y2 + 5у + 1 = 0; б) у2 — 5у + 3 = 0; в) 3у2 — 11у + 9 = 0; г) 3у2 + 7у + 3 = 0; д) у2 — 5у + 3 = 0; е) y2 – 10y + 12 = 0; ж) 9y2 — 18у + 5 = 0; з) 9у2 — 45у + 50 = 0.

3. Пусть корни квадратного уравнения 6х2 — 5х — 2 = 0 равны х1 и х2. Не решая уравнения, найдите:

Ответы:

4. Корни квадратного уравнения aх2 + bх + с = 0 равны х1 и х2. Найдите:

Ответы:

5. Корни квадратного уравнения ах2 + bх + с = 0 равны х1 и х2. Напишите квадратное уравнение, корни которого равны:

Ответы: а) аy2 – bу + с = 0; б) ay2 + 3bу + 9с = 0; в) ау2 + (b — 2а)у + (с – b + а) = 0; г) су2 + bу + а = 0.

6. Найдите корни квадратного уравнения ах2 + bх + с = 0, если:

а) а + b + с = 0; б) 4a + 2b + с = 0; в) а — b + с = 0; г) 4а – 2b + с = 0.

Ответы:

7а). При каком значении параметра а сумма квадратов корней уравнения х2 + (2 — а)х – а — 3 = 0 наименьшая? Найдите ее.

7б). При каком значении параметра а сумма квадратов корней уравнения х2 + (а — 1)x + а2 — 1,5 = 0 наибольшая? Найдите ее.

Ответы: а) а = 1 и х12 + х22 = 9; б) а = -1 и х12 + х22 = 5.

VIII. Подведение итогов урока

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

© 2014-2022 Все права на дизайн сайта принадлежат С.Є.А.

Сумма обратных величин корней уравнения

Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.

ХОД УРОКА

I. Сообщение темы и цели урока

II. Общая характеристика контрольной работы

Контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).

При проверке вариантов 1, 2 оценка «5» ставится за правильное решение пяти задач, оценка «4» — четырех задач и оценка «3» — трех задач. Одна задача является резервной (или запасной) и дает некоторую свободу выбора учащимся. При таких же критериях оценки за решение задач вариантов 3, 4 дается дополнительно 0,5 балла, вариантов 5, 6 — 1 балл (т. е. оценку «5» можно получить за правильное решение четырех задач).

III. Контрольная работа в 6 вариантах

Вариант 1

1. Решите уравнение 5х 2 + 10х = 0.
2. Решите уравнение 9x 2 – 4 = 0.
3. Решите уравнение х 2 – 7х + 6 = 0.
4. Решите уравнение 2x 2 + 3х + 4 = 0.
5. Один из корней уравнения х 2 + ах + 72 = 0 равен 9. Найдите другой корень и коэффициент а.
6. Периметр прямоугольника равен 26 см, а его площадь — 36 см 2 . Найдите длины сторон прямоугольника.

Вариант 2

1. Решите уравнение 6х 2 + 18х = 0.
2. Решите уравнение 4х 2 – 9 = 0.
3. Решите уравнение x 2 – 8x + 7 = 0.
4. Решите уравнение 3х 2 + 5x + 6 = 0.
5. Один из корней уравнения x 2 + 11х + а = 0 равен 3. Найдите другой корень и коэффициент а.
6. Периметр прямоугольника равен 22 см, а его площадь — 24 см 2 . Найдите длины сторон прямоугольника.

Вариант 3

1. Решите уравнение 2x 2 – 7х + 5 = 0.
2. Решите уравнение (2х – 1) 2 – 9 = 0.
3. Решите уравнение х 2 + 2ах – 3а 2 = 0.
4. Напишите квадратное уравнение с целыми коэффициентами, корни которого –3 и 1 /₂.
5. Катер прошел по течению реки 30 км и 24 км против течения за 9 ч. Чему равна собственная скорость катера, если скорость течения реки равна 3 км/ч?
6. Найдите сумму квадратов корней уравнения x 2 + рх + q = 0.

Вариант 4

1. Решите уравнение 3x 2 – 7х + 4 = 0.
2. Решите уравнение (3x + 1) 2 – 4 = 0.
3. Решите уравнение x 2 – 3ах – 4а 2 = 0.
4. Напишите квадратное уравнение с целыми коэффициентами, корни которого –2 и 1 /₃.
5. Моторная лодка прошла 45 км по течению реки и 22 км против течения, затратив на весь путь 5 ч. Найдите скорость лодки в стоячей воде, если скорость течения реки 2 км/ч.
6. Найдите сумму обратных величин корней уравнения x 2 + рх + q = 0.

Вариант 5

1. Решите уравнение 6x 2 + х – 2 = 0.
2. Решите уравнение (3х + 1) 2 = (х + 2) 2 .
3. Решите уравнение x 2 – х – а 2 + а = 0.
4. Даны четыре последовательных целых числа. Сумма произведений двух крайних и двух средних чисел равна 22. Найдите эти числа.
5. Найдите наименьшее значение суммы корней уравнения x 2 + (8а – а 2 )х – а 4 = 0.
6. Уравнение x 2 + Зх – 2а 2 – 0 имеет корни х₁ и x₂. Напишите квадратное уравнение, корни которого равны х₁ + 1 и x₂ + 1.

Вариант 6

1. Решите уравнение 9x 2 + 3х – 2 = 0.
2. Решите уравнение (4х + 3) 2 = (2х – 1) 2 .
3. Решите уравнение x 2 + 3х – 4а 2 + 6а = 0.
4. Даны четыре последовательных целых числа. Сумма произведений двух крайних и двух средних чисел равна 38. Найдите эти числа.
5. Найдите наибольшее значение суммы корней уравнения x 2 + (а 2 – 6а)х – 3а 2 = 0.
6. Уравнение x 2 + 2х – 3а 2 = 0 имеет корни х₁ и x₂. Напишите квадратное уравнение, корни которого равны х₁ – 1 и x₂ – 1.

IV. Подведение итогов контрольной работы

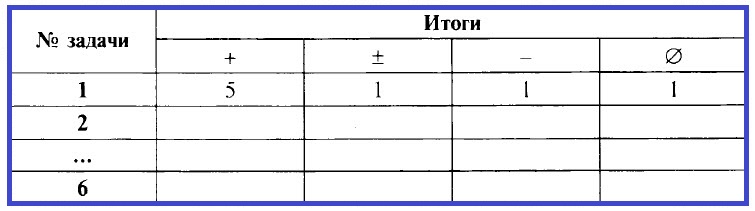
1. Распределение работ по вариантам и результаты решения. Данные о результатах работы удобно заносить в таблицу (для каждой пары вариантов).

Обозначения:
+ (число решивших задачу правильно или почти правильно);
± (число решивших задачу со значительными погрешностями);
– (число не решивших задачу);
∅ (число не решавших задачу).

1. Типичные ошибки, возникшие при решении задач.
2. Наиболее трудные задачи и их разбор (учителем или школьниками, решившими их).
3. Разбор всей контрольной работы (вывесить на стенде ответы к заданиям и разобрать наиболее трудные варианты).

V. Разбор задач ( ответы и решения )

VI. Подведение итогов урока

Вы смотрели: Поурочное планирование по алгебре для 8 класса. УМК Макарычев (Просвещение). ГЛАВА III. КВАДРАТНЫЕ УРАВНЕНИЯ. § 7. Применение свойств арифметического квадратного корня (11 ч). Урок 53. Контрольная работа № 5 по теме «Квадратные уравнения» + ОТВЕТЫ и РЕШЕНИЯ.

8.2.4. Применение теоремы Виета

Часто требуется найти сумму квадратов (x₁ 2 +x₂ 2 ) или сумму кубов (x₁ 3 +x₂ 3 ) корней квадратного уравнения, реже — сумму обратных значений квадратов корней или сумму арифметических квадратных корней из корней квадратного уравнения:

Помочь в этом может теорема Виета:

Сумма корней приведенного квадратного уравнения x 2 +px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

Выразим через p и q:

1) сумму квадратов корней уравнения x 2 +px+q=0;

2) сумму кубов корней уравнения x 2 +px+q=0.

Решение.

1) Выражение x₁ 2 +x₂ 2 получится, если взвести в квадрат обе части равенства x₁+x₂=-p;

(x₁+x₂) 2 =(-p) 2 ; раскрываем скобки: x₁ 2 +2x₁x₂+ x₂ 2 =p 2 ; выражаем искомую сумму: x₁ 2 +x₂ 2 =p 2 -2x₁x₂=p 2 -2q. Мы получили полезное равенство: x₁ 2 +x₂ 2 =p 2 -2q.

2) Выражение x₁ 3 +x₂ 3 представим по формуле суммы кубов в виде:

Еще одно полезное равенство: x₁ 3 +x₂ 3 =-p·(p 2 -3q).

Примеры.

3) x 2 -3x-4=0. Не решая уравнение, вычислите значение выражения x₁ 2 +x₂ 2 .

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения

x₁+x₂=-p=3, а произведение x₁∙x₂=q=-4. Применим полученное нами (в примере 1) равенство:

x₁ 2 +x₂ 2 =p 2 -2q. У нас -p=x₁+x₂=3 → p 2 =3 2 =9; q=x₁x₂=-4. Тогда x₁ 2 +x₂ 2 =9-2·(-4)=9+8=17.

4) x 2 -2x-4=0. Вычислить: x₁ 3 +x₂ 3 .

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения x₁+x₂=-p=2, а произведение x₁∙x₂=q=-4. Применим полученное нами (в примере 2) равенство: x₁ 3 +x₂ 3 =-p·(p 2 -3q)=2·(2 2 -3·(-4))=2·(4+12)=2·16=32.

Ответ: x₁ 3 +x₂ 3 =32.

Вопрос: а если нам дано не приведенное квадратное уравнение? Ответ: его всегда можно «привести», разделив почленно на первый коэффициент.

5) 2x 2 -5x-7=0. Не решая, вычислить: x₁ 2 +x₂ 2 .

Решение. Нам дано полное квадратное уравнение. Разделим обе части равенства на 2 (первый коэффициент) и получим приведенное квадратное уравнение: x 2 -2,5x-3,5=0.

По теореме Виета сумма корней равна 2,5; произведение корней равно -3,5.

Решаем так же, как пример 3), используя равенство: x₁ 2 +x₂ 2 =p 2 -2q.

x₁ 2 +x₂ 2 =p 2 -2q=2,5 2 -2∙(-3,5)=6,25+7=13,25.

Ответ: x₁ 2 +x₂ 2 =13,25.

6) x 2 -5x-2=0. Найти:

Преобразуем это равенство и, заменив по теореме Виета сумму корней через -p, а произведение корней через q, получим еще одну полезную формулу. При выводе формулы использовали равенство 1): x₁ 2 +x₂ 2 =p 2 -2q.

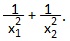
В нашем примере x₁+x₂=-p=5; x₁∙x₂=q=-2. Подставляем эти значения в полученную формулу:

7) x 2 -13x+36=0. Найти:

Преобразуем эту сумму и получим формулу, по которой можно будет находить сумму арифметических квадратных корней из корней квадратного уравнения.

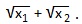
У нас x₁+x₂=-p=13; x₁∙x₂=q=36. Подставляем эти значения в выведенную формулу:

Совет: всегда проверяйте возможность нахождения корней квадратного уравнения по подходящему способу, ведь 4 рассмотренные полезные формулы позволяют быстро выполнить задание, прежде всего, в тех случаях, когда дискриминант — «неудобное» число. Во всех простых случаях находите корни и оперируйте ими. Например, в последнем примере подберем корни по теореме Виета: сумма корней должна быть равна 13, а произведение корней 36. Что это за числа? Конечно, 4 и 9. А теперь считайте сумму квадратных корней из этих чисел: 2+3=5. Вот так то!