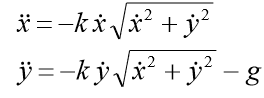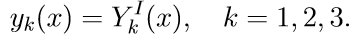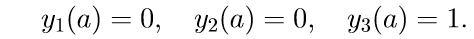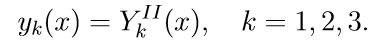Суть численного решения дифференциальных уравнений
Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,у’)=0 или у’=f(x,y). Функция y(x), при подстановке которой уравнение обращается в тождество, называется решением дифференциального уравнения.
Рассмотрим несколько численных методов решения дифференциальных уравнений первого порядка. Описание численных методов приводится для уравнения в виде у’=f(x,y).
Рассмотрим два варианта вывода расчетных формул
Численное решение математических моделей объектов заданных системами дифференциальных уравнений
Введение:
При математическом моделировании ряда технических устройств используются системы дифференциальных нелинейных уравнений. Такие модели используются не только в технике, они находят применение в экономике, химии, биологии, медицине, управлении.
Исследование функционирования таких устройств требуют решения указанных систем уравнений. Поскольку основная часть таких уравнений являются нелинейными и нестационарными, часто невозможно получить их аналитическое решение.
Возникает необходимость использовать численные методы, наиболее известным из которых является метод Рунге — Кутты [1]. Что касается Python, то в публикациях по численным методам, например [2,3], данных по применение Рунге — Кутты крайне мало, а по его модификации — методу Рунге-Кутта-Фельберга вообще нет.
В настоящее время, благодаря простому интерфейсу, наибольшее распространение в Python имеет функцию odeint из модуля scipy.integrate. Вторая функция ode из этого модуля реализует несколько методов, в том числе и упомянутый пятиранговый метод Рунге-Кутта-Фельберга, но, вследствие универсальности, имеет ограниченное быстродействие.
Целью настоящей публикации является сравнительный анализ перечисленных средств численного решения систем дифференциальных уравнений с модифицированным автором под Python методом Рунге-Кутта-Фельберга. В публикации так же приведены решения по краевым задачам для систем дифференциальных уравнений (СДУ).
Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
Для одного дифференциального уравнения n – го порядка, задача Коши состоит в нахождении функции, удовлетворяющей равенству:
и начальным условиям
Перед решением эта задача должна быть переписана в виде следующей СДУ
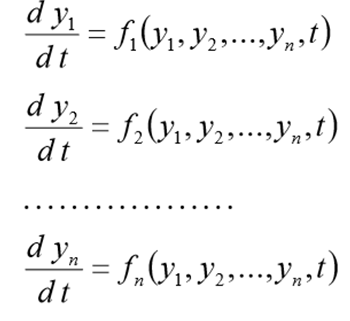
с начальными условиями
Модуль имеет две функции ode() и odeint(), предназначенные для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (задача Коши). Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.
Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат odeint(func, y0, t[,args=(), . ]) Аргумент func – это имя Python функции двух переменных, первой из которых является список y=[y1,y2. yn], а второй – имя независимой переменной.
Функция func должна возвращать список из n значений функций 
Второй аргумент y0 функции odeint() является массивом (или списком) начальных значений 
Третий аргумент является массивом моментов времени, в которые вы хотите получить решение задачи. При этом первый элемент этого массива рассматривается как t0.
Функция odeint() возвращает массив размера len(t) x len(y0). Функция odeint() имеет много опций, управляющих ее работой. Опции rtol (относительная погрешность) и atol (абсолютная погрешность) определяют погрешность вычислений ei для каждого значения yi по формуле
Они могут быть векторами или скалярами. По умолчанию
Вторая функция модуля scipy.integrate, которая предназначена для решения дифференциальных уравнений и систем, называется ode(). Она создает объект ОДУ (тип scipy.integrate._ode.ode). Имея ссылку на такой объект, для решения дифференциальных уравнений следует использовать его методы. Аналогично функции odeint(), функция ode(func) предполагает приведение задачи к системе дифференциальных уравнений вида (1) и использовании ее функции правых частей.
Отличие только в том, что функция правых частей func(t,y) первым аргументом принимает независимую переменную, а вторым – список значений искомых функций. Например, следующая последовательность инструкций создает объект ODE, представляющий задачу Коши.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
При численном решении задачи Коши
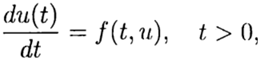

по известному решению в точке t =0 необходимо найти из уравнения (3) решение при других t. При численном решении задачи (2),(3) будем использовать равномерную, для простоты, сетку по переменной t с шагом т > 0.
Приближенное решение задачи (2), (3) в точке 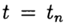

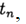


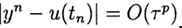

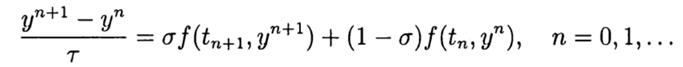
При 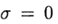
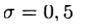
Явные схемы второго и более высокого порядка аппроксимации удобно строить, ориентируясь на метод предиктор-корректор. На этапе предиктора (предсказания) используется явная схема
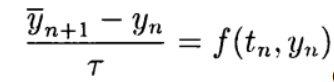
а на этапе корректора (уточнения) — схема
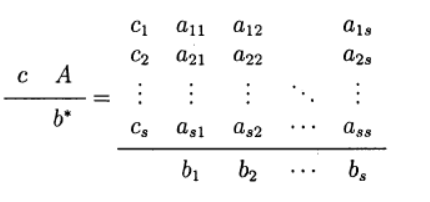
В одношаговых методах Рунге—Кутта идеи предиктора-корректора реализуются наиболее полно. Этот метод записывается в общем виде:

Формула (6) основана на s вычислениях функции f и называется s-стадийной. Если 
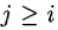

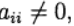

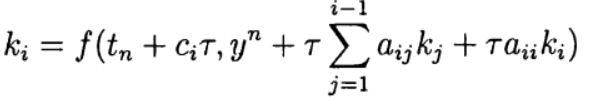
О таком методе Рунге—Кутта говорят как о диагонально-неявном. Параметры 
Одним из наиболее распространенных является явный метод Рунге—Кутта четвертого порядка

Метод Рунге—Кутта— Фельберга
Привожу значение расчётных коэффициентов 
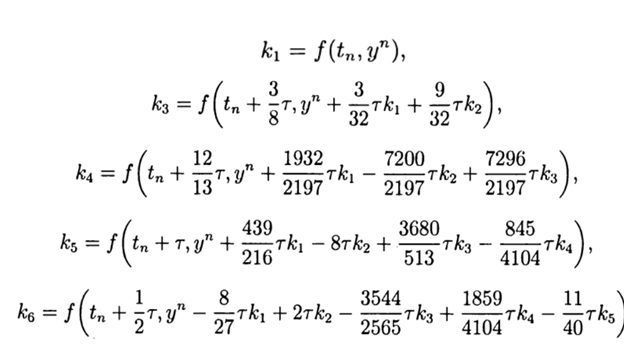
С учётом(9) общее решение имеет вид:
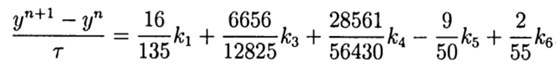
Это решение обеспечивает пятый порядок точности, остаётся его адаптировать к Python.
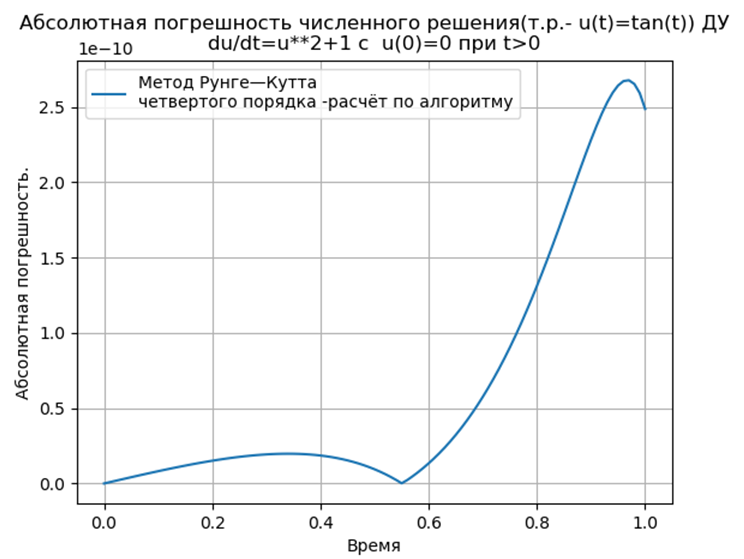
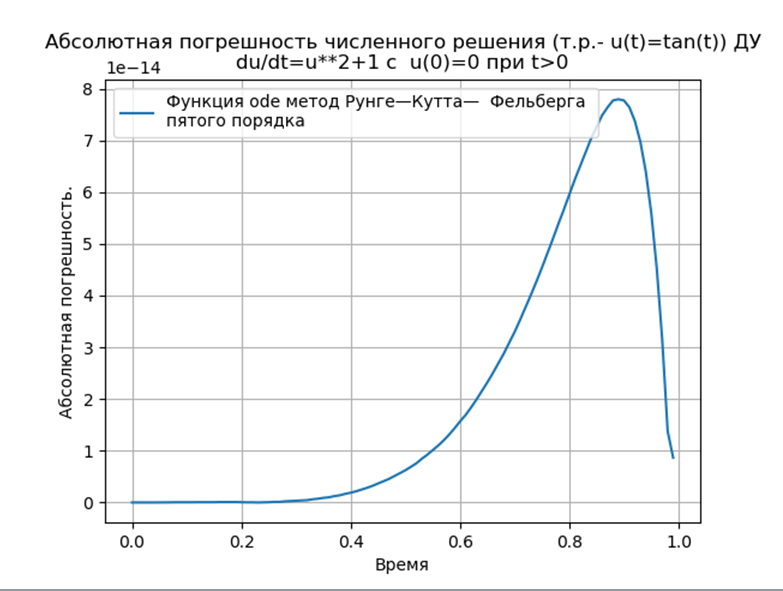
Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения  с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
Адаптированные к Python методы Рунге—Кутта и Рунге—Кутта— Фельберга имеют меньшую абсолютную, чем решение с применением функции odeint, но большую, чем с использованием функции edu. Необходимо провести исследование быстродействия.
Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
Сравнительный анализ проведём на примере модельной задачи, приведенной в [2]. Чтобы не повторять источник, приведу постановку и решение модельной задачи из [2].
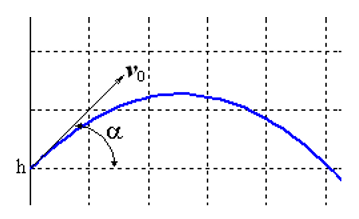
Решим задачу Коши, описывающую движение тела, брошенного с начальной скоростью v0 под углом α к горизонту в предположении, что сопротивление воздуха пропорционально квадрату скорости. В векторной форме уравнение движения имеет вид
где 



Особенность этой задачи состоит в том, что движение заканчивается в заранее неизвестный момент времени, когда тело падает на землю. Если обозначить 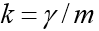
К системе следует добавить начальные условия: 

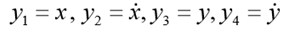
Для модельной задачи положим 
Flight time = 1.2316 Distance = 5.9829 Height =1.8542
Flight time = 1.1016 Distance = 4.3830 Height =1.5088
Flight time = 1.0197 Distance = 3.5265 Height =1.2912
Flight time = 0.9068 Distance = 2.5842 Height =1.0240
Время на модельную задачу: 0.454787
Для реализации средствами Python численного решения СДУ без использования специальных модулей, мною была предложена и исследована следующая функция:
def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6
Функция increment(f, t, y, tau) обеспечивает пятый порядок численного метода решения. Остальные особенности программы можно посмотреть в следующем листинге:
Время на модельную задачу: 0.259927
Предложенная программная реализация модельной задачи без использования специальных модулей имеет почти в двое большее быстродействие, чем с функцией ode, однако нельзя забывать, что ode имеет более высокую точность численного решения и возможности выбора метода решения.
Решение краевой задачи с поточно разделёнными краевыми условиями
Приведем пример некоторой конкретной краевой задачи с поточно разделенными краевыми условиями:
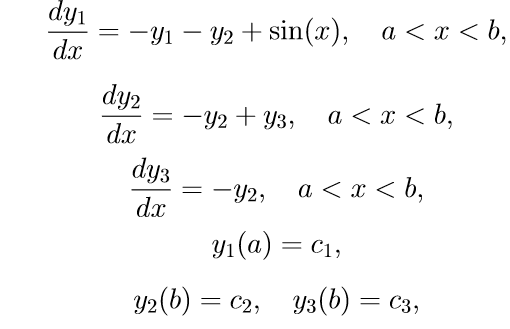
Для решения задачи (11) используем следующий алгоритм:
1. Решаем первые три неоднородные уравнения системы (11) с начальными условиями 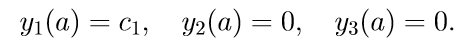
Введем обозначение для решения задачи Коши:
2. Решаем первые три однородные уравнения системы (11) с начальными условиями 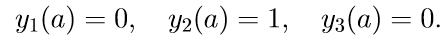
Введем обозначение для решения задачи Коши:
3. Решаем первые три однородные уравнения системы (11) с начальными условиями
Введем обозначение для решения задачи Коши:
4. Общее решение краевой задачи (11) при помощи решений задач Коши записывается в виде линейной комбинации решений: 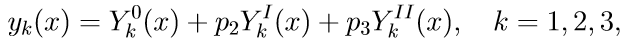
где p2, p3 — некоторые неизвестные параметры.
5. Для определения параметров p2, p3, используем краевые условия последних двух уравнений (11), то есть условия при x = b. Подставляя, получим систему линейных уравнений относительно неизвестных p2, p3:

Решая (12), получим соотношения для p2, p3.
По приведенному алгоритму с применением метода Рунге—Кутта—Фельберга получим следующую программу:
y0[0]= 0.0
y1[0]= 1.0
y2[0]= 0.7156448588231397
y3[0]= 1.324566562303714
y0[N-1]= 0.9900000000000007
y1[N-1]= 0.1747719838716767
y2[N-1]= 0.8
y3[N-1]= 0.5000000000000001
Время на модельную задачу: 0.070878
Вывод
Разработанная мною программа отличается от приведенной в [3] меньшей погрешностью, что подтверждает приведенный в начале статьи сравнительный анализ функции odeint с реализованным на Python метода Рунге—Кутта—Фельберга.
3. Н.М. Полякова, Е.В. Ширяева Python 3. Создание графического интерфейса пользователя (на примере решения методом пристрелки краевой задачи для линейных обыкновенных дифференциальных уравнений). Ростов-на-Дону 2017.
Понятие о численных методах решения обыкновенных дифференциальных уравнений
Описание: Недостатки метода Эйлера 4. Идея метода Эйлера очень проста. В результате приходим к приближённому уравнению: Поскольку по определению у= окончательно имеем следующее уравнение являющееся основой метода Эйлера: 8 Конечно это уравнение является лишь приближённым и мы надеемся что чем меньше величина шага h тем оно будет более точным уменьшается локальная погрешность метода то есть погрешность на одном его шаге.
Дата добавления: 2015-08-14
Размер файла: 153.35 KB
Работу скачали: 23 чел.
Поделитесь работой в социальных сетях
Если эта работа Вам не подошла внизу страницы есть список похожих работ. Так же Вы можете воспользоваться кнопкой поиск
Понятие о численных методах решения обыкновенных дифференциальных уравнений
Содержание
1. Метод Эйлера
2. О решении ОДУ высших степеней и их систем
3. Недостатки метода Эйлера
4. Четырёхточечный метод Рунге-Кутты
5. Вычислительный эксперимент
Литература
Рассмотрим дифференциальное уравнение первого порядка, разрешенное относительно производной, то есть уравнение вида
относительно неизвестной функции y = y ( x ). Правая часть этого уравнения представляет собой известную функцию двух переменных х и у. Например, рассматриваемое ОДУ может иметь вид
Обратим внимание на то, что при рассмотрении задач механики у нас встречались производные по времени, которые принято обозначать точками над соответствующими переменными. В настоящем же разделе мы рассматриваем функции переменной х и возвращаемся к стандартному обозначению производной от функции штрихом над её символом.
С помощью численных методов мы будем искать частные решения соответствующих дифференциальных уравнений. Впрочем, в большинстве физических приложений требуется отыскание именно таких решений. Действительно, при отправлении, например, космического аппарата с Земли на Марс, нам необходимо найти не все возможные траектории его движения в Солнечной Системе (что соответствовало бы общему решению соответствующей системы ОДУ!), а одну-единственную траекторию, начинающуюся в некоторой точке на Земле и заканчивающуюся в месте желаемой посадки космического аппарата на Марсе. Как уже отмечалось в разделе 1.2 для выделения частного решения из общего необходимо задать некоторые условия, например, начальные условия или краевые.
Уравнение (1) является уравнением первого порядка и поэтому его общее решение зависит лишь от одной произвольной постоянной. В связи с этим для выделения частного решения достаточно задать лишь одно начальное условие:
Это условие означает, что при фиксированном значении аргумента искомая функция у(х) должна иметь некоторое известное значение .
Таким образом, перед нами стоит вопрос о решении простейшей задачи Коши, которая определяется заданием дифференциального уравнения и некоторого начального условия (более подробно смотри далее):
Приведённую задачу Коши мы собираемся решать численно. Что это означает? Всем хорошо известны из школьного курса физики «Четырёхзначные математические таблицы» Брадиса. В них разные функции, в частности тригонометрические, задаются в табличной форме: в первой колонке указаны дискретные значения аргумента, например =0.1, 0.2, 0.3, 0.4,…, а в соседней колонке соответствующие им значения табулируемой функции, например, синуса: sin (0.1), sin (0.2), sin (0.3), sin (0.4),….
Аналогичным образом численное решение рассматриваемой нами задачи Коши будет представлено в форме таблицы значений аргумента
и соответствующих им значений функции у(), которая является решением дифференциального уравнения (1). Для краткости, значение функции у(х) при аргументе мы будем обозначать символом .
Шаг табулирования h предполагается достаточно малым. Величина его, очевидно, зависит от решаемой нами задачи. Например, при описании движения траектории Земли, возможно, вполне достаточно будет в качестве временного шага выбрать один день (55 точек на одном обороте Земли вокруг Солнца), но вряд ли кому-нибудь потребуется при решении этой задачи выбрать в качестве величины этого шага одну микросекунду.
Очевидно, что, чем быстрее изменяется функция, тем меньше должен быть шаг аргумента при её табуляции для того, чтобы через найденное множество точек можно было провести достаточно плавный график рассматриваемой функции.
Кстати заметим, что при построении графика функции на экране компьютера (например, в математическом пакете Maple ) первоначально строится некоторая достаточно подробная таблица этой функции, после чего соседние точки, отвечающие значениям табулируемой функции соединяются отрезками прямых (возможно, конечно, и соединение точек более сложными кривыми это проблема изучается в теории аппроксимации функций, являющейся одним из разделов численного анализа). Итак, итогом численного решения задачи Коши (3) должна явиться таблица вида:
Первая строка этой таблицы содержит известные нам величины, входящие в начальное условие (3 b ) и . Во второй строке аргумент =+ h известен по построению, а (то есть значение функции у()) является неизвестным.
Идея метода Эйлера очень проста. По определению производной,
В случае производной от функции у(х) в точке х=имеем
поскольку в нашем случае . Если шаг h достаточно мал , то приближённое значение производной () можно найти, опуская предел в формуле (5), т.е. полагая
С другой стороны, уравнение (3а), по определению, справедливо при любом значении аргумента х и , стало быть, оно верно и в точках :
Подставим теперь в это точное равенство приближённое выражение для первой производной (6). В результате приходим к приближённому уравнению:
Поскольку, по определению у()=, окончательно имеем следующее уравнение, являющееся основой метода Эйлера:
Конечно, это уравнение является лишь приближённым, и мы надеемся, что, чем меньше величина шага h , тем оно будет более точным (уменьшается локальная погрешность метода, то есть погрешность на одном его шаге).
Заметим, что в численном анализе не принято писать знак приближённого равенства, вместо него используется знак точного равенства (по умолчанию предполагается, что все формулы численного анализа являются приближёнными).
Полагая k =0 из уравнения (8) имеем
Все величины в правой части этого уравнения нам известны (см. начальные условия (3 b )), что даёт возможность вычислить неизвестное значение и заполнить тем самым вторую строку таблицы 1.
Полагая далее k =1, из уравнения (8) имеем
Поскольку было определено на предыдущем шаге метода, в правой части последнего уравнения также известны все величины и можно найти , что позволяет заполнить следующую строку таблицы 1.
Продолжая действовать таким образом и далее, можно заполнить таблицу 1 вплоть до сколь угодно большого значения аргумента . В этом и заключается суть метода Эйлера.
Таким образом, решение дифференциального уравнения свелось к многократному применению рекуррентного соотношения (8). Формулы типа (8) называются явными, поскольку их применение даёт в явном виде значения функции у(х) в следующей точке () по ранее уже найденным значениям функции у(х) в предыдущих точках. 1
Из рассмотренной выше вычислительной схемы метода Эйлера со всей очевидностью следует, что она одинаково применима для любого дифференциального уравнения первого порядка: как линейного, так и нелинейного. 2
2. О решении ОДУ высших степеней и их систем
Мы разобрали технику применения метода Эйлера для численного решения уравнения первого порядка. С другой стороны, в обсуждавшиеся ранее математические модели входили уравнения второго порядка, что, фактически, связано с применением второго закона Ньютона. В связи с этим возникает вопрос: как решать ОДУ высших порядков и их системы?
Оказывается, что метод Эйлера, как, впрочем, и другие численные методы, пригодные для решения задачи Коши (3), можно достаточно легко обобщить на случай решения систем уравнений первого порядка в канонической форме (см. далее), а уравнения высших степеней сводятся к таким системам уравнений. Сведение дифференциального уравнения высшего порядка к системе уравнений первого порядка достигается с помощью введения дополнительных переменных, равных последовательным производным неизвестной функции, входящей в это уравнение. В случае уравнения второго порядка типа уравнений гармонического осциллятора или математического маятника достаточно ввести только одну новую переменную, причем имеющую ясный физический смысл. Она является скоростью (линейной в случае уравнения гармонического осциллятора или угловой в случае математического маятника).
При рассмотрении уравнения математического маятника положим . Тогда и уравнение можно записать в форме следующих двух уравнений первого порядка
Рассматривая эти уравнения для момента времени имеем
Согласно основной идее метода Эйлера заменим точные значения производных, входящих в уравнения (9), их допредельными образами:
где шаг по времени, с которым решается рассматриваемое ОДУ. Здесь Подстановка соотношений (11) в уравнения (10) приводит нас к следующим уравнениям метода Эйлера
Полагая k =0,1,2,3 и т. д., мы будем получать последовательные значения угла и соответствующие ему значения угловой скорости u ( t ) в последовательные моменты времени
Совершенно аналогичным образом систему двух ОДУ второго порядка, которая описывает движения планет вокруг Солнца (31), можно свести к системе из четырёх уравнений первого порядка, если ввести две дополнительные переменные, представляющие собой скорости движения тела m вдоль координатных осей х и у соответственно:
Тогда исследуемая система принимает вид:
Заменяя в системе (12) каждую производную её допредельным образом, получаем явные формулы для решения этой системы методом Эйлера.
3. Недостатки метода Эйлера
Существует простая геометрическая интерпретация метода Эйлера. Рассмотрим снова задачу Коши (3) для одного ОДУ первой степени и соответствующее ему в методе Эйлера рекуррентное соотношение (8)
На плоскости (х,у) каждому частному решению задачи Коши, которая выделяется начальным условием , отвечает некоторая кривая, которая называется интегральной кривой. Изменяя , мы переходим от одной к другой интегральной кривой. Более того, можно доказать, что через каждую точку плоскости (х,у) проходит одна и только одна интегральная кривая 3 .
Пусть решению рассматриваемой нами задачи Коши на рис. 1 отвечает жирная интегральная кривая. Рекуррентное уравнение метода Эйлера (8) можно записать в форме
Поскольку, согласно решаемому нами ОДУ, . Если считать параметр h непрерывной переменной, то легко понять, что уравнение (13) представляет собой уравнение касательной, проведённой в точке к интегральной кривой у(х), проходящей через эту точку.
Таким образом, на каждом шаге метода Эйлера мы заменяем истинную интегральную кривую отрезком касательной, проведённой к этой кривой в начале микроинтервала [,]. Тем самым мы отклоняемся от искомой интегральной кривой на некоторую маленькую величину, причём её малость определяется малостью шага h .
В результате, на втором шаге метода Эйлера мы строим касательную в точке не к истинной, а к другой интегральной кривой той, которая проходит через эту точку и, таким образом, ещё больше отклоняемся от искомой интегральной кривой, удовлетворяющей начальному условию .
Таким образом, в методе Эйлера мы заменяем искомую интегральную кривую некоторой ломаной линией, которая, по мере отдаления от начальной точки , всё более и более отклоняется от этой интегральной кривой. Иными словами, абсолютная погрешность метода Эйлера имеет тенденцию к нарастанию по мере увеличения числа шагов этого метода.
Может показаться, что если выбрать шаг интегрирования h более маленьким, то можно существенным образом уменьшить эту погрешность. В общем случае это, однако, не так. Действительно, если мы должны получить решение исходной задачи Коши (3) на некотором заданном макроинтервале [,], то уменьшение шага h влечёт за собой увеличение числа шагов интегрирования N , поскольку . «Локальная погрешность» (погрешность на одном шаге) уменьшается при уменьшении h , но увеличение числа шагов может привести к росту «глобальной погрешности» на заданном интервале [,]. Вышеуказанная ситуация характерна для неустойчивых вычислительных процессов, использование которых на практике может привести к катастрофическим последствиям. В силу этого, необходимо рассматривать такие методы численного решения ОДУ, которые порождают достаточно устойчивые численные алгоритмы. 4 Весьма распространёнными и хорошо зарекомендовавшими себя на практике для решения ОДУ являются методы Рунге-Кутты. Это целый класс методов и мы, в качестве примера, рассмотрим так называемый четырёхточечный метод Рунге-Кутты
4. Четырёхточечный метод Рунге-Кутты
Ниже кратко описано применение четырёхточечного метода Рунге-Кутты для решения задачи Коши (11) для дифференциального уравнения первого порядка, разрешённого относительно производной. Таким образом, мы будем рассматривать ту же самую задачу Коши, решение которой ранее рассматривалось методом Эйлера.
Заметим, прежде всего, что решение дифференциального уравнения (3а) фактически определяет зависимость первой производной от двух независимых переменных х и у. Это очень хорошо видно из рис. 1: фиксируя х, мы имеем бесконечное множество значение производной , поскольку каждая из пересекаемых вертикальной линией х= const интегральных кривых имеет своё направление касательной.
Описываемый метод Рунге-Кутты, как и метод Эйлера, состоит из последовательности шагов величиной h , но, в отличие от последнего метода, на каждом шаге h находится не одно значение производной (в методе Эйлера находилось лишь ), а несколько. Они соответствуют разным значениям аргументов функции f (х,у). В четырёхточечном методе Рунге-Кутты (откуда и происходит его название) находится четыре различных значения и делается некоторое специфическое их усреднение (то есть берётся не простое среднее арифметическое значение этих производных!). После этого делается перемещение из точки в точку по прямой в направлении тангенса угла наклона, которое определяется этим усреднённым значением производной. Заметим, что разные варианты методов Рунге-Кутты отличаются друг от друга стратегией выбора точек, в которых находятся производные на микроинтервале h и формулой усреднения значения этих производных.
Рассмотрим детально эту процедуру для одного шага метода Рунге-Кутты, который приводит к увеличению аргумента х на величину h , то есть определяет переход от значения к значению . Один такой шаг состоит из следующих четырёх этапов.
Этап I . Находим производную к интегральной кривой в точке 1 с координатами , подставляя эти координаты в правую часть дифференциального уравнения, т.е. вычисляя значение . Из точки
1: перемещаемся на полшага вперёд по прямой, направление которой задаётся этим значением производной (то есть по прямой с тангенсом угла наклона к оси абсцисс, равным значению (этот этап метода Рунге-Кутты полностью аналогичен шагу метода Эйлера с шагом h /2). В результате, в плоскости (х,у) мы переходим в точку
Этап II . Через найденную таким образом точку 2 проходит своя интегральная кривая и мы находим направление касательной к ней, то есть вычисляем значение производной
Далее делается полшага вперёд с найденным значением производной (), но снова из начальной точки микроинтервала [,]. Таким образом, мы переходим в плоскости (х,у) в точку
Этап III . В этой точке находим значение производной , подставляя её координаты в правую часть дифференциального уравнения:
Эта производная определяет направление касательной к интегральной кривой, проходящей через точку 3.
Этап IV . Из начальной точки 1: делаем на сей раз полный шаг вперёд (на величину h по оси х) по прямой, в направлении, которое определяется значением производной . В результате мы переходим в точку
Находим производную в этой точке подстановкой её координат в правую часть дифференциального уравнения:
В результате четырёх описанных выше этапов мы нашли четыре значения производных. Производим их усреднение по формуле
Таким образом, является некоторым средневзвешенным значением найдённых четырёх производных: двум «внутренним» значениям производном соответствуют весовые множители 2, а двум крайним множители 1 [деление в формуле (14) производится на сумму этих четырёх весовых множителей: 6=1+2+2+1].
Далее мы перемещаемся по прямой из начальной точки 1: в направлении, тангенс угла наклона которого к оси абсцисс определяется средним значением производной из формулы (14). Таким образом, из начальной точки с координатами переходим в точку плоскости (х,у) с координатами
Иными словами, полный шаг метода Рунге-Кутты определяется формулами
В теории методов Рунге-Кутты строго доказывается, что именно такое усреднении четырёх значений производной, найденное вышеуказанным методом, даёт наилучшее приближение к правильному результату для значения неизвестной функции у(х) на правом конце микроинтервала .
Более того, порядок точности рассматриваемого метода Рунге-Кутты на одном шаге величины h оценивается формулой
где . Здесь есть пятая производная от искомого решения дифференциального уравнения (3а) в некоторой точке на микроинтервале . Таким образом, локальная погрешность метода Рунге-Кутты (то есть погрешность на одном шаге h ) пропорциональна пятой степени шага h и пятой производной искомого решения дифференциального уравнения.
Оценки точности типа (16) позволяют грубо оценить величину шага интегрирования шага h , необходимого для достижения требуемой точности решения исходного дифференциального уравнения. Для метода Эйлера аналогичная погрешность на одном шаге определяется формулой
Таким образом, четырёхточечный метод Рунге-Кутты на три порядка по шагу точнее метода Эйлера (например, при h =0.01 точность метода Рунге-Кутты в миллион раз выше точности метода Эйлера).
Более того, оказывается, что метод Рунге-Кутты порождает достаточно устойчивый вычислительный процесс и может, таким образом, применяться для решения широких классов дифференциальных уравнений.
Обобщение четырёхточечного метода Рунге-Кутты на случай решения систем дифференциальных уравнений в каноническом виде может быть сделано в полной аналогии с тем, как это делается для метода Эйлера. При этом на каждом этапе метода Рунге-Кутты идёт вычисление четырёх наборов производных, соответствующих всем искомым функциям , которые определяются дифференциальными уравнениями
Эти уравнения и представляют собой систему ОДУ в канонической форме.
Последнее замечание. При решении задач в рамках настоящего пособия мы будем использовать математический пакет Maple , который предоставляет достаточно широкие возможности для численного решения ОДУ (можно использовать разные численные методы) и построения графиков их решений. Таким образом, при решении предлагаемых в пособии задач студентам не придётся сами программировать метод Рунге-Кутты или какие-либо другие методы численного решения дифференциальных уравнений.
Численное (а по возможности, и аналитическое) решение ОДУ на языке Maple осуществляется с помощью оператора dsolve , с разными спецификациями, которые, в частности, позволяют выбрать необходимый метод численного интегрирования. По умолчанию используется некоторая модификация чеитырёхточечного метода Рунге-Кутты, которая получила название метода Рунге-Кутты-Фельдберга. Она осуществляет решение ОДУ с переменным шагом, величина которого подбирается в зависимости от скорости изменения искомого решения (то есть от крутизны соответствующей интегральной кривой).
5. Вычислительный эксперимент
В предыдущих разделах рассматривались понятия математической модели и дифференциальных уравнений, которые составляют неотъемлемую часть большинства таких моделей, по крайней мере тех, которые мы обсуждаем в настоящем пособии. Мы обсудили также простейшие численные методы решения дифференциальных уравнений. Таким образом, у нас есть средства для численного исследования разнообразных математических моделей, описываемых дифференциальными уравнениями. Теперь настаёт черёд постановки соответствующих вычислительных (компьютерных) экспериментов, с помощью которых и проводится исследование рассматриваемых математических моделей, описывающих изучаемые физические явления.
Суть вычислительного эксперимента заключается в том, что с помощью некоторой компьютерной программы мы проводим численное исследование рассматриваемой нами математической модели, варьируя различные входящие в модель параметры.
Чаще всего результатом вычислительного эксперимента является некоторая числовая информация, выдаваемая компьютером в виде таблиц и (или) графиков. Например, мы проводим расчеты возможных траекторий полёта космического аппарата с учётом различных факторов, влияющих на этот полёт, пытаясь найти в том или ином смысле оптимальный вариант.
По-видимому, наиболее интересными являются те задачи, решение которых заключается в анализе качественно различных режимов поведения системы в зависимости от задаваемого набора свободных параметров математической модели. Такая постановка задачи является очень типичной при исследовании проблем нелинейной физики. При этом роль вычислительного эксперимента вполне аналогична роли натурного физического эксперимента. Заметив некоторый особый режим поведения рассматриваемой нами модели, мы в дальнейшем пытаемся выяснить физическую природу данного физического явления. Может быть, для этого придётся построить некоторую приближённую аналитическую теорию, поставить ряд реальных физических экспериментов, подтверждающих или, наоборот опровергающих результаты численного эксперимента (что вполне возможно в случае ошибочности построения математической модели или неучёта в ней каких-либо существенных факторов). 5
Таким образом, вычислительный эксперимент может сыграть существенную эвристическую роль, натолкнув исследователя на некоторые новые физические идеи. Приведённая в начале настоящего пособия краткая история зарождения солитонной физики была нацелена как раз на то, чтобы оттенить именно эту идею.
Подведём итоги. Суть вычислительной физики заключается в построении математических моделей, адекватных изучаемым физическим явлениям, в разработке соответствующих приближённых аналитических и численных методов и в исследовании этих моделей с помощью проведения соответствующих вычислительных (компьютерных) экспериментов. Особенно эффективны методы вычислительной физики при рассмотрении соответствующих задач нелинейной физики, где очень редко удаётся получить какие-либо точные аналитические результаты.
Все описанные в настоящем разделе идеи будут подробно рассмотрены нами на примерах исследования ряда проблем классической механики, вполне доступных для понимания студентов младших курсов. Рассмотрение же математических моделей из других областей физики может потребовать привлечения знаний квантовой механики, электродинамики, физики твёрдого тела, теории квантовых полей и т.д., знание которых на втором курсе физического факультета ещё не предполагается.
Касьянов В.И.: Руководство к решению задач по высшей математике. — М.: Юрайт, 2011
НИУ БелГУ ; гл. ред. Л.Я. Дятченко: Научные ведомости Белгородского государственного университета. — Белгород: ИПК НИУ «БелГУ», 2011
Чеканов Н.А.: Применение дифференциальных уравнений в курсе общей физики. — Белгород: НИУ БелГУ, 2011
Абрамочкин Е.Г.: Современная оптика гауссовых пучков. — М.: ФИЗМАТЛИТ, 2010
Алексеев Г.В.: Оптимизация в стационарных задачах тепломассопереноса и магнитной гидродинамики. — М.: Научный мир, 2010
Бирман М.Ш.: Избранные труды. — Ижевск: Ижевский институт компьютерных исследований, 2010
Козлов В.В.: Избранные работы по математике, механике и математической физике. — Ижевск: НИЦ «Регулярная и хаотическая динамика» ; , 2010
Лакс П.Д.: Гиперболические дифференциальные уравнения в частых производных. — Ижевск: Ижевский ин-т компьютерных исследований, 2010
Николаевский В.Н.: Собрание трудов. Геомеханика. — Ижевск: Ижевский институт компьютерных исследований, 2010
НИУ БелГУ ; гл. ред. Л.Я. Дятченко: Научные ведомости Белгородского государственного университета. — Белгород: БелГУ, 2010
Новосадов Б.К.: Методы математической физики молекулярных систем. — М.: ЛИБРОКОМ, 2010
1 В отличие от явных формул, широко применяются также и неявные формулы для численного решения дифференциальных уравнений. Применение их не даёт сразу готовый результат, а лишь некоторую систему нелинейных или линейных (уже не дифференциальных!) уравнений, которую необходимо решать теми или иными численными методами.
2 В нелинейном ОДУ функция f(x,y) нелинейным образом зависит от функции у(х).
3 Интегральные кривые не пересекаются. В противном случае, в данной точке (х,у) можно было бы указать две разные касательные =f(x,у), что противоречит предположению об однозначности f(x,y).
4 Подробное рассмотрение вопросов устойчивости различных алгоритмов решения ОДУ можно найти, например, в [5]
5 Впрочем, авторы статьи [6] пишут, что «в настоящее время численное моделирование в физике конденсированного состояния достигло такого уровня доверия, что иногда возникают сомнения в результатах лабораторного эксперимента, если результаты выполненных экспериментов ему противоречат.»
http://habr.com/ru/post/418139/
http://refleader.ru/jgernaqasrnaujg.html
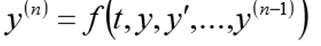
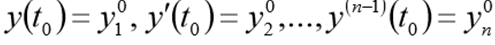


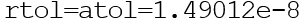
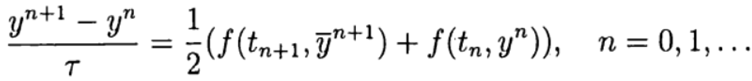
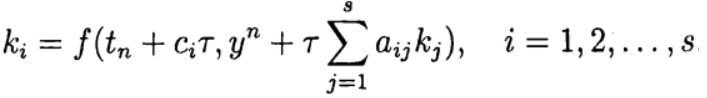
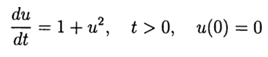 с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга