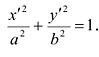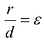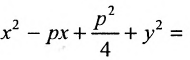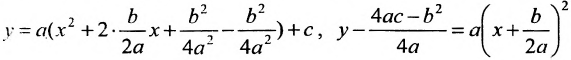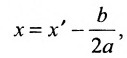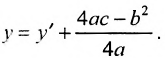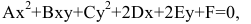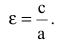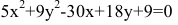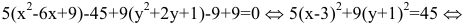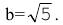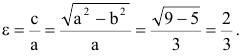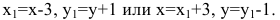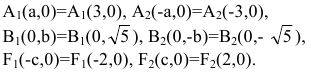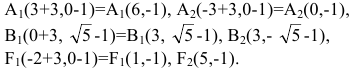Метод исключения — сведение системы ДУ к одному уравнению
Частным случаем канонической системы дифференциальных уравнений является одно уравнение n-го порядка, разрешенное относительно старшей производной.
Введением новых функций
это уравнение заменяется нормальной системой уравнений
Можно утверждать и обратное, что, вообще говоря, нормальная система уравнений первого порядка
эквивалентна одному уравнению порядка . На этом основан один из методов интегрирования систем дифференциальных уравнений — метод исключения .
Проиллюстрируем этот метод на примере системы двух уравнений:
Здесь — постоянные коэффициенты, а и — заданные функции; и — искомые функции. Из первого уравнения системы (1) находим
Подставляя во второе уравнение системы вместо у правую часть (2), а вместо производную от правой части (2), получаем уравнение второго порядка относительно
где — постоянные. Отсюда находим . Подставив найденное выражение для и в (2), найдем .
Пример 1. Проинтегрировать систему уравнений
Решение. Из первого уравнения системы (3) находим , тогда
Подставляя (4) во второе уравнение системы (3), получаем линейное дифференциальное уравнение с постоянными коэффициентами второго порядка
Общее решение уравнения (5)
Находя производную по от (6), получаем
Общее решение системы (3):
Пример 2. Решить задачу Коши для системы
Решение. Из второго уравнения системы (7) находим
Подставляя (9) и (10) в первое уравнение системы (7), получаем уравнение , общее решение которого
Подставляя (11) в (9), найдем . Общее решение системы (7)
При начальных условиях (8) из (12) получим систему уравнений для определения
решая которую, найдем . Подставляя эти значения и в (12), получаем решение поставленной задачи Коши:
Пример 3. Решить систему уравнений
Решение. Из первого уравнения системы находим
Подставляя эти выражения для и во второе уравнение, получаем
Считая , из последнего уравнения имеем и после интегрирования получим . Теперь легко находим
Общее решение данной системы
Замечание. Не всякая система дифференциальных уравнений может быть сведена к одному уравнению более высокого порядка. Например,
не сводится к одному уравнению второго порядка. Ее общее решение .
Кривые второго порядка — определение и построение с примерами решения
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 
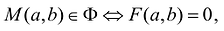
Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
Эллипс
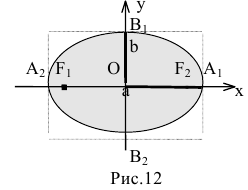
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 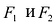
Точки 
Если а =Ь, то уравнение (7.3) можно переписать в виде:
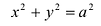
Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 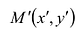
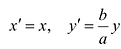
Число 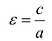
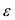
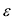
Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 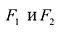
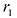
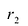
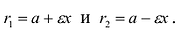
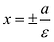
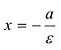
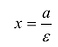
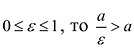
Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 
Точки 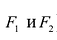
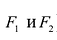
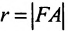
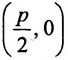
Тогда 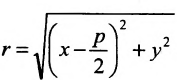
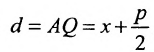
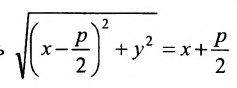
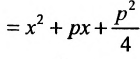
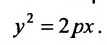
Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 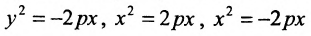
Легко показать, что уравнение 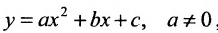
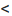
и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 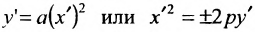
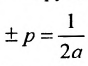
Пример:
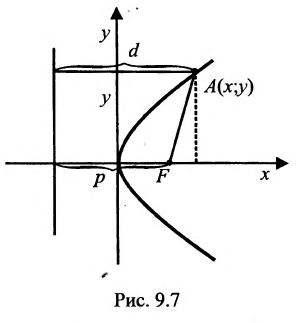
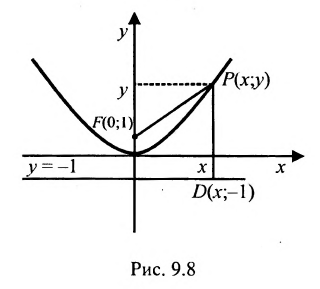
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию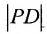
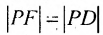
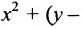
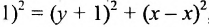
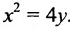
Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
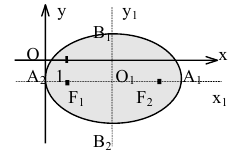
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению
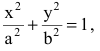
Число а называют большей полуосью эллипса, число 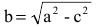
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки 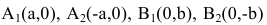
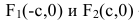
Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 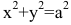
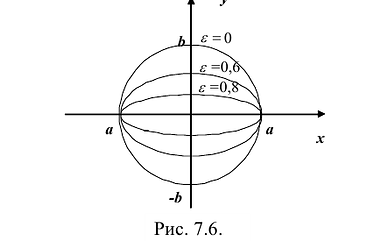
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 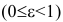
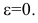
Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:
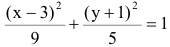
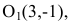
Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 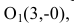
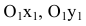
В новой системе координат координаты 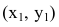
Переходя к старым координатам, получим:
Построим график эллипса.
Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Дифференциальные уравнения, приводимые к уравнениям первого порядка
Вы будете перенаправлены на Автор24
Дифференциальные уравнения второго порядка, в которых правая часть не зависит от неизвестной функции и её производной
Таким дифференциальным уравнением второго порядка является уравнение вида $y»=f\left(x\right)$. В нем правая часть не зависит от неизвестной функции $y$ и её производной $y’$, а зависит только от $x$. Решается это уравнение последовательным интегрированием.
Представим его в таком виде: $\frac
Интегрируем первый раз, используя то свойство, что неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: $\int d\left(y’\right) =\int f\left(x\right)\cdot dx $ или $y’=\int f\left(x\right)\cdot dx +C_ <1>$, где $C_ <1>$ — произвольная постоянная.
Таким образом, дифференциальное уравнение второго порядка сведено теперь к дифференциальному уравнению первого порядка, которое можно представить в таком виде: $dy=\left(\int f\left(x\right)\cdot dx +C_ <1>\right)\cdot dx$.
Интегрируем полученное дифференциальное уравнение повторно: $y=\int \left(\int f\left(x\right)\cdot dx +C_ <1>\right)\cdot dx =\int \left(\int f\left(x\right)\cdot dx \right)\cdot dx +\int C_ <1>\cdot dx$. Окончательно получаем:$y=\int \left(\int f\left(x\right)\cdot dx \right)\cdot dx +C_ <1>\cdot x+C_ <2>$, где $C_ <2>$ — произвольная постоянная.
Процесс интегрирования завершен. Получена неизвестная функция $y$, которая является общим решением данного дифференциального уравнения второго порядка.
Алгоритм решения дифференциального уравнения второго порядка $y»=f\left(x\right)$ может быть представлен в следующем виде:
- находим интеграл $I_ <1>\left(x\right)=\int f\left(x\right)\cdot dx $ и записываем первую производную искомой функции в виде $y’\left(x,C_ <1>\right)=I_ <1>\left(x\right)+C_ <1>$;
- находим интеграл $I_ <2>\left(x\right)=\int I_ <1>\left(x\right)\cdot dx $ и записываем окончательно общее решение данного дифференциального уравнения: $y=I_ <2>\left(x\right)+C_ <1>\cdot x+C_ <2>$;
- для поиска частного решения начальные условия подставляем в выражение для первой производной $y’$, а также в общее решение; в результате находим значения произвольных постоянных $C_ <1>$ и $C_ <2>$.
Готовые работы на аналогичную тему
Найти общее решение дифференциального уравнения второго порядка $y»=4$. Записать также его частное решение, которое удовлетворяет начальным условиям $y=1$ при $x=1$, $y’=1$ при $x=1$.
В данном дифференциальном уравнении правая часть не зависит ни от неизвестной функции $y$, ни от её производной $y’$. Следовательно, оно решается последовательным интегрированием два раза подряд.
Находим интеграл $I_ <1>\left(x\right)=\int f\left(x\right)\cdot dx =\int 4\cdot dx =4\cdot x$. Записываем выражение для первой производной в виде $y’\left(x,C_ <1>\right)=I_ <1>\left(x\right)+C_ <1>$, то есть $y’=4\cdot x+C_ <1>$.
Находим интеграл $I_ <2>\left(x\right)=\int I_ <1>\left(x\right)\cdot dx =\int 4\cdot x\cdot dx =2\cdot x^ <2>$. Записываем окончательно общее решение в виде $y=I_ <2>\left(x\right)+C_ <1>\cdot x+C_ <2>$. Получаем: $y=2\cdot x^ <2>+C_ <1>\cdot x+C_ <2>$.
Ищем частное решение. Подставляем начальное условие $y’=1$ при $x=1$ в выражение для $y’$: $1=4\cdot 1+C_ <1>$, откуда $C_ <1>=-3$. Подставляем начальное условие $y=1$ при $x=1$ в выражение для $y$: $1=2\cdot 1^ <2>+\left(-3\right)\cdot 1+C_ <2>$, откуда $C_ <2>=2$. Таким образом, частное решение имеет вид: $y=2\cdot x^ <2>-3\cdot x+2$.
Дифференциальные уравнения второго порядка, не содержащие неизвестной функции
Указанные дифференциальные уравнения второго порядка допускают понижение порядка посредством замены переменных. После этого к полученным дифференциальным уравнениям первого порядка могут быть применены известные методы решения.
Дифференциальное уравнение второго порядка, не содержащее неизвестной функции $y$, имеет вид $y»=f\left(x,y’\right)$.
Для его решения применяют замену $y’=z\left(x\right)$.
При этом $y»=z’\left(x\right)$. После подстановки данное дифференциальное уравнение приобретает вид дифференциального уравнения первого порядка относительно $z$, то есть $z’=f\left(x,z\right)$. Решая его, находим $z\left(x\right)=\phi \left(x,C_ <1>\right)$.
В свою очередь, поскольку $y’=z\left(x\right)$, то $y’=\phi \left(x,C_ <1>\right)$. Это также дифференциальное уравнение первого порядка, которое допускает непосредственное интегрирование. Следовательно, интегрируя еще раз, окончательно получаем общее решение $y=\int \phi \left(x,C_ <1>\right)\cdot dx +C_ <2>$.
Алгоритм решения дифференциального уравнения второго порядка $y»=f\left(x,y’\right)$ может быть представлен в следующем виде:
- переписываем данное дифференциальное уравнение в виде дифференциального уравнения первого порядка относительно переменной $z$, формально заменив $y»$ на $z’$, а $y’$ — на $z$;
- полученное дифференциальное уравнение первого порядка решаем одним из подходящих известных методов;
- найденное решение $z=\phi \left(x,C_ <1>\right)$ представляем в виде дифференциального уравнения первого порядка $y’=\phi \left(x,C_ <1>\right)$, которое допускает непосредственное интегрирование;
- находим интеграл $I=\int \phi \left(x,C_ <1>\right)\cdot dx $ и получаем общее решение в виде $y=I+C_ <2>$.
Найти общее решение дифференциального уравнения$y»-\frac
Данное дифференциальное уравнение не содержит неизвестной функции $y$, поэтому переписываем его в виде дифференциального уравнения первого порядка относительно переменной $z$, формально заменив $y»$ на $z’$, а $y’$ — на $z$. Получаем: $z’-\frac
Это дифференциальное уравнение первого порядка является линейным неоднородным, решая которое известным методом, получаем $z=\left(3\cdot x+C_ <1>\right)\cdot x$.
Найденное решение представляем в виде дифференциального уравнения первого порядка $y’=\phi \left(x,C_ <1>\right)$, то есть $y’=\left(3\cdot x+C_ <1>\right)\cdot x$. Это дифференциальное уравнение допускает непосредственное интегрирование.
Находим интеграл $I=\int \phi \left(x,C_ <1>\right)\cdot dx =\int \left(3\cdot x+C_ <1>\right)\cdot x\cdot dx =x^ <3>+C_ <1>\cdot \frac
Дифференциальные уравнения второго порядка, не содержащие независимой переменной
Указанные дифференциальные уравнения второго порядка также допускают понижение порядка посредством замены переменных. После этого к полученным дифференциальным уравнениям первого порядка могут быть применены известные методы решения.
Дифференциальное уравнение второго порядка, не содержащее независимой переменной $x$, имеет вид $y»=f\left(y,y’\right)$.
Для его решения применяют замену $y’=z\left(y\right)$.
Подставляем выражения для $y’$ и $y»$ в данное дифференциальное уравнение: $z\cdot \frac
В свою очередь, поскольку $\frac
Алгоритм решения дифференциального уравнения второго порядка $y»=f\left(y,y’\right)$ может быть представлен в следующем виде:
- переписываем данное дифференциальное уравнение в виде дифференциального уравнения первого порядка относительно переменной $z$, формально заменив $y»$ на $z\cdot z’$, а $y’$ — на $z$;
- полученное дифференциальное уравнение первого порядка решаем одним из подходящих известных методов;
- найденное решение $z=\phi \left(y,C_ <1>\right)$ представляем в виде дифференциального уравнения первого порядка $\frac
=\phi \left(y,C_ <1>\right)$, которое является дифференциальным уравнением с разделяющимися переменными; - находим интеграл $I=\int \frac
<\phi \left(y,C_<1>\right)> $ и получаем общее решение в виде $I=x+C_ <2>$.
http://www.evkova.org/krivyie-vtorogo-poryadka
http://spravochnick.ru/matematika/differencialnye_uravneniya/differencialnye_uravneniya_privodimye_k_uravneniyam_pervogo_poryadka/