Дифференциальные уравнения первого порядка, приводящиеся к линейным
Метод решения
К линейным уравнениям первого порядка приводится уравнения вида:
(1) ,
где z – функция от y ; p и q – функции от x .
Действительно, по правилу дифференцирования сложной функции:
.
Подставляя в (1), получаем уравнение, линейное относительно z :
.
Дифференциальные уравнения, линейные относительно переменной x
Ранее мы рассматривали уравнения, линейные относительно переменной y . То есть мы считали, что x является независимой переменной, а y является зависимой переменной. Однако, всегда стоит иметь в виду, что возможен противоположный подход. То есть можно считать переменную y независимой переменной, а x – зависимой переменной. На практике часто встречаются задачи, в которых уравнение линейно относительно переменной x , а не y . В общем виде такое уравнение можно записать так:
(2) ,
где P, Q, R –функции от y .
Покажем, что это уравнение линейно относительно переменной x . Для этого выполняем преобразования. Представим производную в виде отношения дифференциалов:
.
Тогда уравнение (2) примет вид:
.
Умножаем на и выполняем алгебраические преобразования:
;
.
Разделив на R ( y ) , приводим уравнение к виду:
,
где .
Это – линейное относительно x дифференциальное уравнение.
Пример решения дифференциального уравнения, приводящегося к линейному уравнению первого порядка
Решить уравнение:
(П.1) .
Подставим в (П.1):
.
Считаем, что y – это независимая переменная, а x – зависимая. То есть x – это функция от y . Умножим на :
(П.2) .
Делаем подстановку:
.
Здесь z – сложная функция от y , .
Дифференцируем по y . По правилу дифференцирования сложной функции:
.
Подставляем в (П.2):
;
.
Это линейное, относительно z , дифференциальное уравнение. Решаем его с помощью интегрирующего множителя. Умножаем уравнение на интегрирующий множитель e y :
;
;
.
Интегрируем по частям:
;
;
;
.
Переходим к переменной x :
;
.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов . Опубликовано: 05-08-2012 Изменено: 26-06-2015
Методика введения решения линейных уравнений и уравнений, сводящихся к линейным
Разделы: Математика
Изучение уравнений в среднем звене начинается с введения решения линейных уравнений и уравнений, сводящихся к линейным.
Равенство двух функций, рассматриваемых в общей области определения, называется уравнением. Переменные, входящие в уравнение, обозначаются латинскими буквами x, y,z, t … Уравнение с одной переменной х в общем, виде записывается так f(x)= g(x).
Всякое значение переменной, при котором выражения f(x) и g(x) принимают равные числовые значения, называется корнем уравнения.
Решить уравнение – это, значит, найти все его корни или доказать, что их нет.
Например, уравнение 3+x=7 имеет единственный корень 4, так как при этом и только при этом значении переменной 3+x=7 верное равенство.
Уравнение (x-1)(x-2)=0 имеет 2 корня 1 и 2.
Уравнение x 2 +1=0 не имеет действительных корней, так как сумма двух положительных чисел не равняется 0.
Для того, чтобы решить любое уравнение с одной переменной, учащийся должен знать: во-первых, правила, формулы или алгоритмы решения уравнений данного вида и, во-вторых, правила выполнения тождественных и равносильных преобразований, с помощью которых данное уравнение можно привести к простейшим.
Таким образом, решение каждого уравнения складывается из двух основных частей:
- преобразования данного уравнения к простейшим;
- решения простейших уравнений по известным правилам, формулам или алгоритмам.
Если вторая часть является алгоритмической, то первая часть — в значительной степени — эвристической, что и представляет наибольшую трудность для учащихся. В процессе решения уравнения его стараются заменить более простым, поэтому важно знать с помощью каких преобразований это возможно. Здесь необходимо в доступной для ребенка форме дать понятие равносильности.
Уравнения, имеющие одни и теже корни, называются равносильными. Равносильными считаются и уравнения, каждое из которых не имеет корней.
Например, уравнения x+2=5 и x+5=8 равносильны, так как каждое из них имеет единственный корень — число 3.Равносильны и уравнения x 2 +1=0 и 2x 2 +5=0 — ни одно из них не имеет корней.
Уравнения х-5=1 и х 2 =36 не равносильны, так как первое имеет только один корень х=6, тогда как второе имеет два корня 6 и –6.
К равносильным преобразованиям относятся:
1) Если к обеим частям уравнения прибавить одно и тоже число или одно и тоже целое алгебраическое выражение, содержащее неизвестное, то новое уравнение будет равносильно данному.
2) Если обе части уравнения умножить или разделить на одно и тоже отличное от нуля число, то получится уравнение, равносильное данному.
Например, уравнение 
3) Если в уравнении произвести раскрытие скобок и привести подобные слагаемые, то получится уравнения, равносильно данному.
Обучение решения уравнений начинается с простейших линейных уравнений и уравнений сводящихся к ним. Дается определение линейного уравнения и рассматриваются случаи, когда оно имеет одно решение; не имеет решений и имеет бесконечное множество решений.
Линейным уравнением с одной переменной х называют уравнение вида ах = b, где а и b — действительные числа, а — называют коэффициентом при переменной, b — свободным членом.
Для линейного уравнения ах = b могут представиться при случае:
- а
0, в этом случае корень уравнения равен b/a
- а = 0; b = 0; в этом случае уравнение принимает вид 0
х = b, что верно при любом х, т.е. корнем уравнения служит любое действительное число;
- а = 0; b
0; в том случае уравнение принимает вид 0
х = b, оно не имеет корней.
Многие уравнения в результате преобразований сводятся к линейным.
Так в 7 классе можно применить следующие уравнения:
1)
Это уравнение сводиться к линейному уравнению.
Умножением обеих частей на 12 (наименьшее общее краткое знаменателей 3, 4, 6, 12), получим:
8 + 3x + 2 – 2x = 5x –12,
8 + 2 + 12 = 5x – 3x + 2x,
2) Покажем, что уравнение 2 (х + 1) – 1 = 3 — (1 — 2х) не имеет корней.
Упростим обе части уравнения:
2х + 2 – 1 = 3 – 1 + 2х,
Это уравнение не имеет корней, т.к. левая часть 0 х равна 0 при любом х, а значит не равна 1.
3) Покажем, что уравнение 3(1 – x) + 2 = 5 – 3x имеет бесконечное множество корней.
При прохождении темы “линейные уравнения с двумя переменными” можно предложить учащимся графический способ решения уравнения. Данный метод основан на пользовании графиков функций, входящих в уравнение. Суть метода: найти абсциссы точек пересечения графиков функций, стоящих в левой и правой частях уравнения. Основывается на выполнение следующих действий:
1) Преобразовать исходное уравнение к виду f(x) = g(x), где f(x) и g(x) функции, графики, которых можно построить.
2) Построить графики функций f(x) и g(x)
3) Определить точки пересечения построенных графиков.
4) Определить абсциссы найденных точек. Они и дадут множество решений исходного уравнения.
5) Записать ответ.
Преимущество данного метода заключается в том, что он позволяет легко определить число корней уравнения. Недостаток в том, что корни в общем случае определяются приближенно.
Следующим этапом в изучении линейных уравнений, являются уравнения с модулями, причем некоторые решения выполняются несколькими способами.
Решение уравнений, содержащих знак модуля и уравнений с параметрами можно назвать деятельностью, близкой к исследовательской. Это обусловлено тем, что выбор метода решения, процесс решения, запись ответа предполагают определенный уровень сформированности умений наблюдать, сравнивать, анализировать, выдвигать и проверять гипотезу, обобщать полученные результаты.
Особой интерес представляют уравнения, содержащие знак модуля.
По определению модуля числа a, имеем:
Число –a может быть отрицательным при a>0; -a положительным при a -1, тогда

Видим, что число 0 принадлежит промежутку. Значит, является корнем. Таким образом, уравнение 
На простых примерах рассмотрим алгоритм решения уравнений с параметрами: область допустимых значений, область определения, общие решения, контрольные значения параметров, типы частных уравнений. Способы их нахождения будут устанавливаться в каждом виде уравнений отдельно.
На базе введенных понятий определим общую схему решения всякого уравнения F(a;x)=0 с параметром а (для случая двух параметров схема аналогична):
- устанавливаются область допустимых значений параметра и область определения;
- определяются контрольные значения параметра, разбивающие область допустимых значений параметра на области однотипности частных уравнений;
- для контрольных значений параметра соответствующие частные уравнения исследуются отдельно;
- находятся общие решения x=f1 (a),…, fk (a) уравнения F(a;x)=0 на соответствующих множествах Аf1,…, Аfk значений параметра;
- составляется модель общих решений, контрольных значений параметра;
- на модели выделяются промежутки значений параметра с одинаковыми общими решениями (области однотипности);
- для контрольных значений параметра и выделенных областей однотипности записываются характеристики всех типов частных уравнений
- Особое место в алгебре отводится линейным уравнениям с параметрами.
Рассмотрим несколько примеров.
| 1. | 2х – 3 = m +1, +1, |
2х – 3 = 
Умножим обе части уравнения на 3, получим
6х — m•х + 12m + 12,

 , при m
, при m  6.
6.Уравнение 2х – 3 + m (х/3 + 4) + 1 имеет множество решений, заданных формулой 
2. 



mx – n = 2x – 2 + 2n + 3xn,
mx – 2x – 3xn = — 2 + 2n +n,
mx – 2x – 3xn = 3n – 2,
x (m – 2 – 3n) = 3n – 2, при m 


Рассмотрим случай, где a = 0, тогда
m = 3n +2, при n 
n = 
m = 3 • 
x(4 – 2 – 3 

x – любое число, кроме x = 1.
б) 3n – 2 
0 • x = b. В этом случае уравнение не имеет решений.
2) a 
m – 2 – 3n 
m 
x = 


3n – 2 
3n + 3n 
6n 

В этом случае уравнение решений не имеет.
Значит, при n = 
(n 


Ответ: 1. n = 

2. n = 0, m = 6n (n 

3. n 




В дальнейшем предлагается рассмотреть решение задач методом составления линейных уравнений. Это сложный процесс, где надо уметь думать, догадываться, хорошо знать фактически материал.
В процессе решения каждой задачи надо четко размечать четыре этапа:
- изучение условия задачи;
- поиск плана решения и его составление;
- оформление найденного решения;
- критический анализ результата решения.
Теперь рассмотрим задачи, при решении которых применяются линейные уравнения.
1. Сплав меди и цинка содержит меди на 640 г. Больше, чем цинка. После того, как из сплава выделили 6/7 содержащейся в нем меди и 60% цинка, масса сплава оказалась равной 200 г. Какова была масса сплава первоначально?
Пусть в сплаве было х г. цинка, тогда меди (640 + х) г. после того, как выделили 6/7 меди и 60% цинка, осталось 1/7 меди и 40% цинка, т.е. 0,4 части. Зная, что масса сплава оказалась равной 200 г., составим уравнение.
1/7 (х + 640) + 0,4•х = 200,
х + 640 + 2,8•х =1400,
Значит, цинка было 200 г., а меди 840 г.
(200 + 640 = 840). 1) 200 + 840 = 1040 (г.) – масса сплава. Ответ: первоначальная масса сплава 1040 г.
2. Сколько литров 60% серной кислоты нужно прибавить к 10 л 30% кислоты, чтобы получить 40% раствор?
Пусть число литров 60% кислоты, которое прибавим х л, тогда раствора чистой кислоты будет 





60х + 300 = 40х + 400,
60х – 40х = 400 – 300,
Значит, нужно прибавить 5 л 60% кислоты.
При изучении темы “Решение линейных уравнений” рекомендуется некоторая историческая справка.
Задачи на решение уравнений первой степени встречаются еще в вавилонских клинописных текстах. В них же есть некоторые задачи, приводящие к квадратным и даже кубическим уравнениям (последние, по-видимому, решались с помощью подбора корней). Древнегреческие математики нашли геометрическую форму решения квадратного уравнения. В геометрической же форме арабский математик Омар Хайям (конец XI – начало XII века н. э.) исследовал кубическое уравнение, хотя и не нашел общей формулы для его решения. Решение кубического уравнения было найдено в начале XVI века в Италии. После того, как Сципиан дель Ферро решил один частный вид таких уравнений в 1535 году, итальянец Тарталья нашел общую формулу. Он доказал, что корни уравнения x 3 + px + q = 0 имеют вид x =
Это выражение обычно называют формулой Кардано, по имени ученого, узнавшего ее от Тартальи и опубликовавшего в 1545 году в своей книге “Великое искусство алгебраических правил”. Ученик Кардано – молодой математик Феррари решил общее уравнение четвертой степени. После этого на протяжении двух с половиной столетий продолжались поиски формулы для решения уравнений пятой степени. В 1823 году замечательный норвежский математик Нильс Хендрик Абель (1802-1829) доказал, что такой формулы не существует. Точнее говоря, он доказал, что корни общего уравнения пятой степени нельзя выразить через его коэффициенты с помощью арифметических действий и операций извлечения корня. Глубокое исследование вопроса об условиях разрешимости уравнений в радикалах провел французский математик Эварист Галуа (1811-1832), погибший на дуэли в возрасте 21 года. Некоторые проблемы теории Галуа решил советский алгебраист И.Т.Шафаревич.
Наряду с поисками формулы для решения уравнения пятой степени велись и другие исследования в области теории алгебраических уравнений. Виета установил связь между коэффициентами уравнений и его корнями. Он доказал, что если x1,…,xn – корни уравнения x n + a1x n-1 +…+an=0, то имеют место формулы:
Литература:
- Журнал “Математика в школе” 6, 1999
- Приложение к газете “Первое сентября”- математика 20, 1999.
- С.И. Туманов “Алгебра”, пособие для учащихся 6-8 классов.
- Н.И. Александров; И. П.Ярандай “Словарь-справочник по математике”.
- О.Б. Епишева; В.И. Крупич “Учить школьников учиться математике”.
- Е.И.Ямщенко “Изучение функций”.
- А.И. Худобин; М.Ф. Шуршалов “Сборник задач по алгебре и элементарным функциям”.
- Ш. А. Алимов, В.А. Ильин “Алгебра 6-8 классы”.
ПРИВЕДЕНИЕ ИСХОДНОГО НЕЛИНЕЙНОГО УРАВНЕНИЯ РЕГРЕССИИ К ЛИНЕЙНОМУ
О лабораторной работе № 2
на тему:
«Определение параметров нестационарного нелинейного уравнения регрессии»
2 курса 221 группы
Содержание
2.ПРИВЕДЕНИЕ ИСХОДНОГО НЕЛИНЕЙНОГО УРАВНЕНИЯ РЕГРЕССИИ К ЛИНЕЙНОМУ………………………………………………………………………………………7 3.ПРОВЕРКА НАЛИЧИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ МЕЖДУ ФАКТОРАМИ МОДЕЛИ……………………………………………………………………………………………8
4.ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ УРАВНЕНИЯ РЕГРЕССИИ. ПОСТРОЕНИЕ УРАВНЕНИЯ РЕГРЕССИИ………………………………………………………………………11
5.ПРОВЕРКА СТАТИСТИЧЕСКОЙ ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ ………. 13
5.1.Проверка случайности колебаний уровней статочной последовательности………. 13
5.2. Проверка соответствия распределения случайной компоненты нормальному закону распределения……………………………………………………………………………………15
5.3.Проверка равенства математического ожидания случайной компоненты нулю………..16
5.4.Проверка независимости значений уровней случайной компоненты……………………17
5.5.Определение точности модели………………………………………………………………18
5.6. Тест ранговой корреляции Спирмена ……………………………………………………….19
6. ПРОВЕРКА НАЛИЧИЯ АНОМАЛЬНЫХ КОЛЕБАНИЙ ИССЛЕДУЕМОЙ МОДЕЛИ..21
7.ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО ВИДА ЛИНИИ ТРЕНДА. ПРОГНОЗ ПОКАЗАТЕЛЕЙ…………………………………………………………………………………..22
Список использованной литературы………………………………………………25
ВВЕДЕНИЕ
Специфической особенностью деятельности экономиста является работа в условиях недостатка информации и неполноты исходных данных. Анализ такой информации требует специальных методов, которые составляют один из аспектов эконометрики. Центральной проблемой эконометрики является построение эконометрической модели и определение возможностей ее использования для описания, анализа и прогнозирования реальных экономических процессов.
Становление и развитие эконометрического метода происходили на основе так называемой высшей статистики — на методах парной и множественной регрессии, парной, частной и множественной корреляции, выделения тренда и других компонент временного ряда, на статистическом основании.
Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целого ряда других вопросов эконометрики. В настоящее время множественная регрессия — один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии — построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.
Задачей данной работы является оценка адекватности и точности нелинейной нестационарной модели уравнения регрессии с использованием персональных компьютеров.
Данная работа состоит из семи глав и трех приложении. Первая глава – постановка задачи.
Во второй главе осуществляется приведение исходного нелинейного уравнения регрессии к линейному по средствам замены переменных.
В третьей главе проверяется наличие мультиколлинеарности между факторами модели.
В главе 4 определяются параметры уравнения регрессии и строится искомое уравнение регрессии.
В пятой главе проверяется статистическая значимость уравнения регрессии. В пункте 5.1. осуществляется проверка колебаний уровней остаточной последовательности при помощи критерия серий, основанного на медиане выборки. В пункте 5.2. проводится проверка соответствия распределения случайной компоненты нормальному закону распределения при помощи показателей ассиметрии и эксцесса. В пункте 5.3. показана проверка равенства математического ожидания случайной компоненты нулю с использованием t-критерия Стьюдента. В пункте 5.4. проверяется независимость значений уровней случайной компоненты с целью выявления существующей автокорреляции остаточной последовательности. В данной работе эта проверка производится при помощи d-критерия Дарбина — Уотсона. В пункте 5.5. определяется точность модели. В качестве статистических показателей точности в данной работе используются следующие: среднеквадратичное отклонение, средняя относительная ошибка аппроксимации, коэффициент сходимости, коэффициент детерминации. В пункте 5.6 проверяется наличие или отсутствие гетероскедастичности исследуемой модели при помощи теста ранговой корреляции Спирмена.
В шестой главе осуществляется проверка на наличие аномальных колебании исследуемой модели с помощью метода Ирвина.
В восьмой главе определяется оптимальный вид линии тренда, которые отражены в приложениях, и прогнозируются показатели.
ПОСТАНОВКА ЗАДАЧИ
В данной работе необходимо рассмотреть нелинейную нестационарную модель изучаемого экономического объекта. В качестве объекта исследования представлен экономический процесс, о котором известны следующие статистические данные:
1. Y(t) — ставка % рефинансирования Центробанка;
2. X1(t) — уровень безработицы, %
3. X2(t) — уровень инфляции, %
Требуется найти коэффициенты нелинейной нестационарной модели уравнения множественной регрессии вида:
Y(t) — ставка % рефинансирования Центробанка;
X1(t) — уровень безработицы, %
X2(t) — уровень инфляции, %
Значения величин Y(t), X1(t), Х2(t) даны в Таблице №1 «Исходные данные». Данное нелинейное уравнение требуется привести к линейному уравнению вида:

Ø определить параметры уравнения регрессии, используя замену переменной;
Ø проверить наличие мультиколлинеарности между факторами;
Ø проверить статистическую значимость уравнения в целом и отдельных коэффициентов уравнения. Это позволит оценить адекватность полученной модели исследуемому процессу и возможность её использования для осуществления анализа и проектирования;
Ø проверить отсутствие гетероскедастичности и автокорреляции остатков исследуемой модели, установить адекватность и точность уравнения регрессии;
Ø проверить наличие аномальных наблюдений, используя метод Ирвина.
Таблица №1
ИСХОДНЫЕ ДАННЫЕ
| T | X1 | X2 | Y |
| 25,22 | |||
| 21,52 | |||
| 22,32 | |||
| 21,77 | |||
| 20,66 | |||
| 20,14 | |||
| 17,66 | |||
| 17,08 | |||
| 16,87 | |||
| 18,63 | |||
| 16,51 | |||
| 16,95 | |||
| 19,38 | |||
| 18,14 | |||
| 17,94 | |||
| 19,69 | |||
| 19,38 | |||
| 15,88 | |||
| 16,58 | |||
| 14,64 |
ПРИВЕДЕНИЕ ИСХОДНОГО НЕЛИНЕЙНОГО УРАВНЕНИЯ РЕГРЕССИИ К ЛИНЕЙНОМУ
Многие экономические процессы наилучшим образом описываются нелинейными уравнениями регрессии. Например, функции спроса и производственные функции. И в этом случае мы не можем применить к ним обычный метод наименьших квадратов и использовать стандартные подходы к оценке статистической надежности.
В связи с этим встает задача о возможности привести нелинейное уравнение к линейному виду.
В тех случаях, когда нелинейность касается факториальных переменных, но не связано с коэффициентами уравнения регрессии, нелинейность обычно устраняется путем замены переменной.
Рассмотрим нелинейное нестационарное уравнение:
Y(t) — ставка % рефинансирования Центробанка;
X1(t) — уровень безработицы, %
X2(t) — уровень инфляции, %
В данном случае нелинейность касается факторных переменных, но не связано с коэффициентами уравнения.
Вводим новые переменные:
Полученное уравнение является линейным как по переменным, так и по параметрам.
http://urok.1sept.ru/articles/410415
http://poisk-ru.ru/s14070t1.html
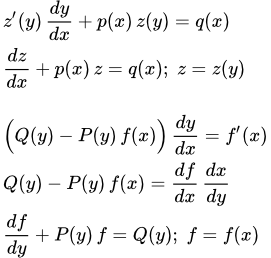
 0, в этом случае корень уравнения равен b/a
0, в этом случае корень уравнения равен b/a х = b, что верно при любом х, т.е. корнем уравнения служит любое действительное число;
х = b, что верно при любом х, т.е. корнем уравнения служит любое действительное число; 0; в том случае уравнение принимает вид 0
0; в том случае уравнение принимает вид 0 х = b, оно не имеет корней.
х = b, оно не имеет корней.







