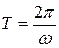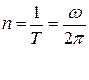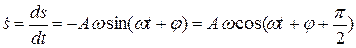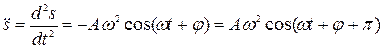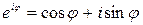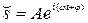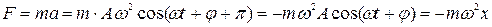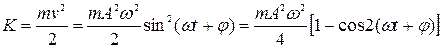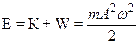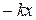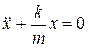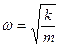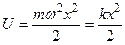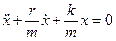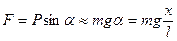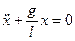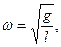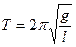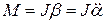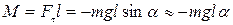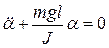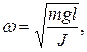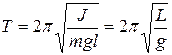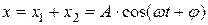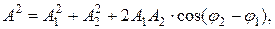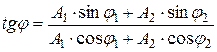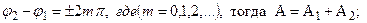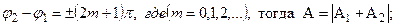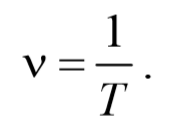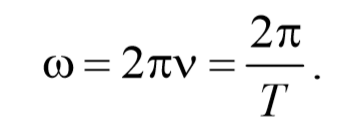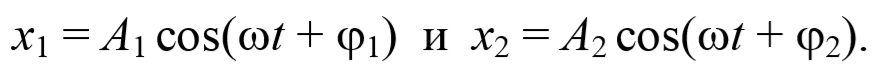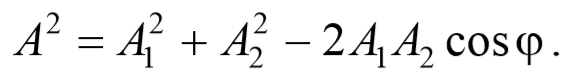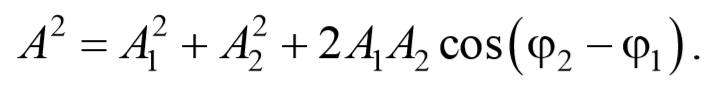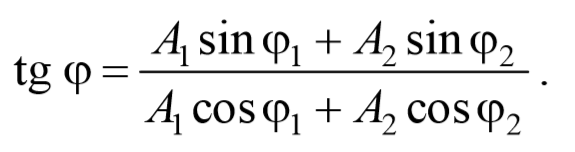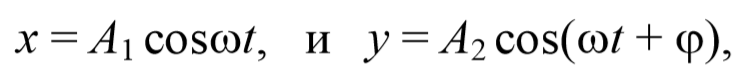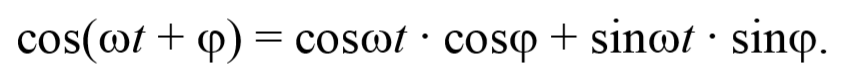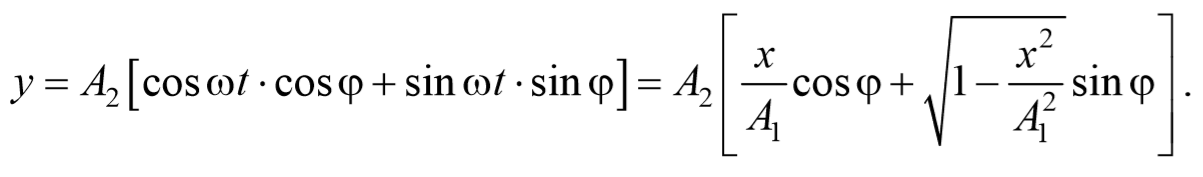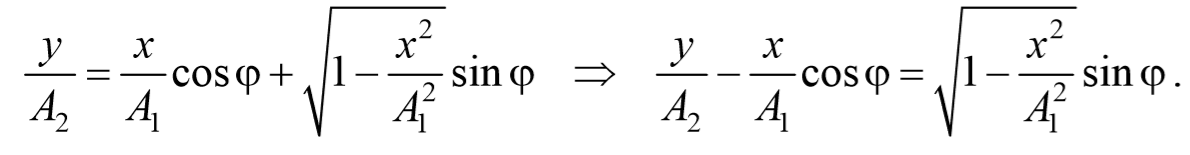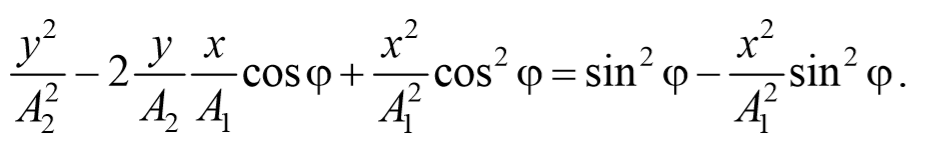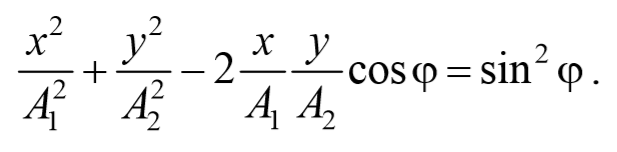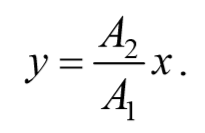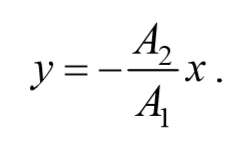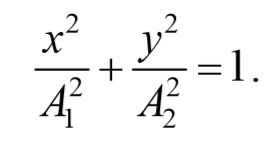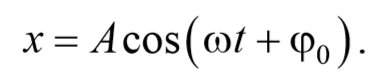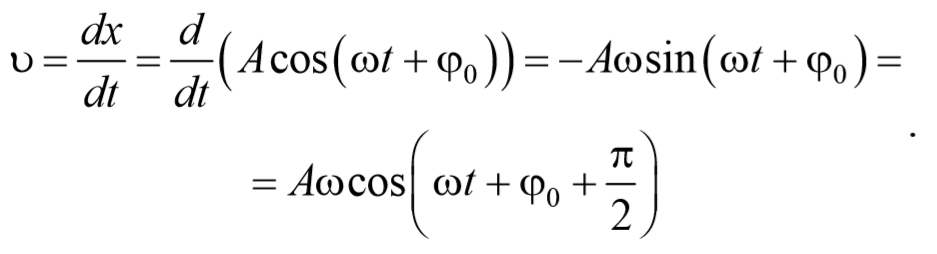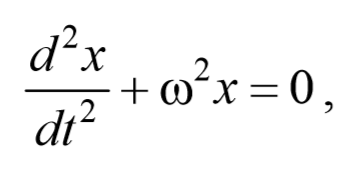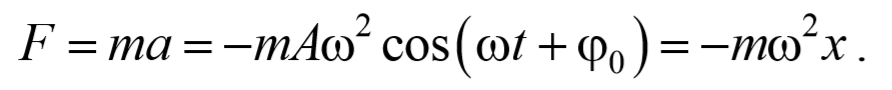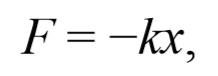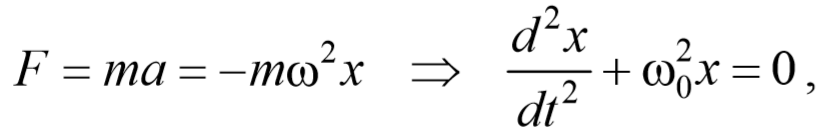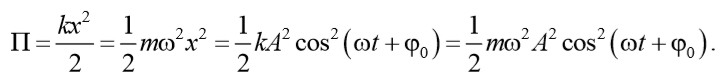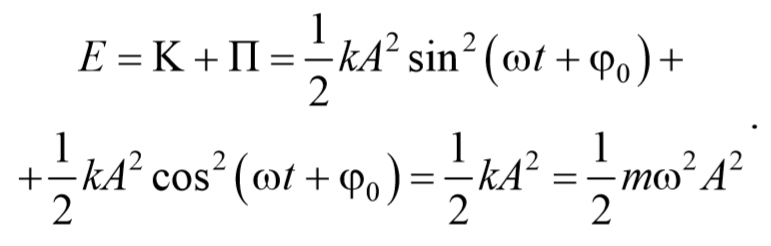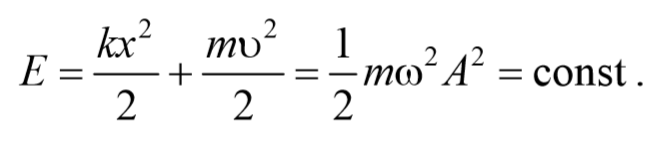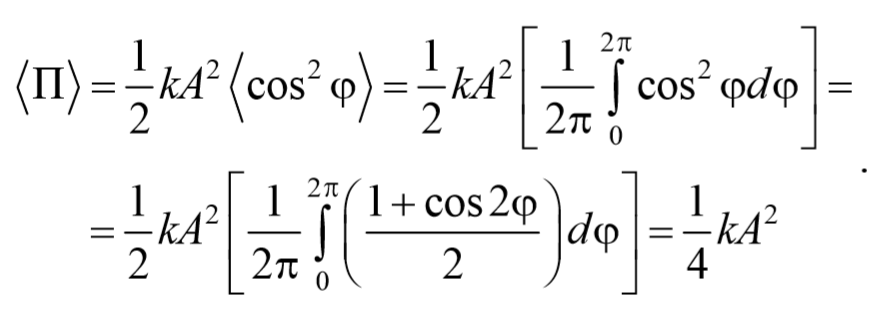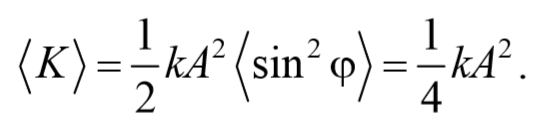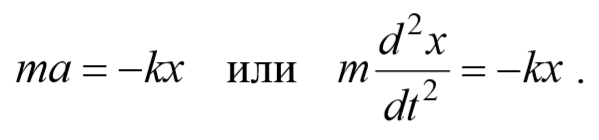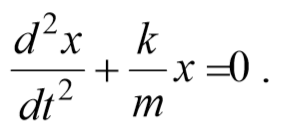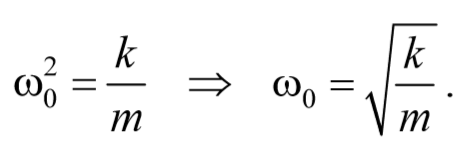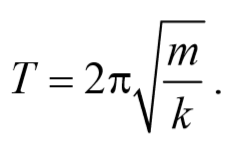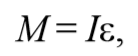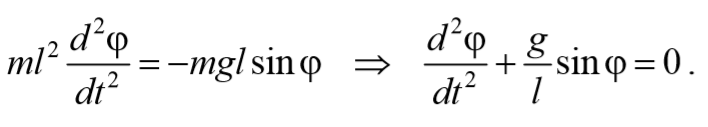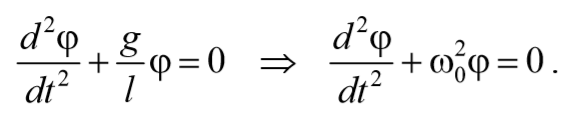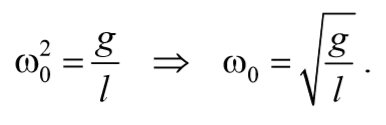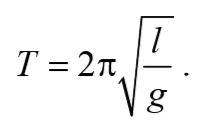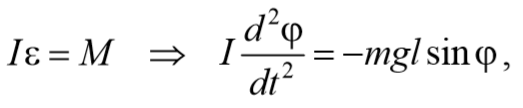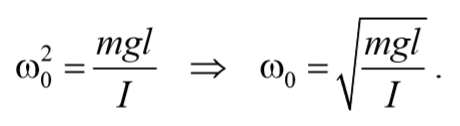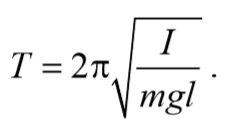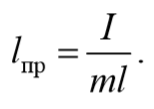Свободные колебания дифференциальное уравнение амплитуда период свободных колебаний

Свободные колебания

1. Колебания. Общий подход к изучению колебаний различной физичес­
кой природы.

Колебаниями называются движения или процессы, которые обладают определенной повторяемостью во времени.

Колебания сопровождаются попеременным превращением энергии одного вида в энергию другого вида.

Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии, без дальнейшего внешнего воздействия на колебательную систему (систему, совершающую колебания). Колебания называются вынужденными, если они происходят под действием периодически изменяющейся внешней силы.

Физическая природа колебаний может быть разной — различают механические, электромагнитные и др. колебания.

Но различные колебательные процессы описываются одинаковыми уравнениями, поэтому целесообразно изучать все колебательные процессы, используя общие свойства колебаний.

2. Гармонические колебания и их характеристики.

Гармоническими колебаниями называются колебания, при которых колеблющаяся физическая величина изменяется по закону синуса (или косинуса).

Различные периодические процессы (процессы, повторяющиеся через равные промежутки времени) могут быть представлены в виде суммы (суперпозиции) гармонических колебаний.

Гармоническое колебание величины s описывается уравнением типа

А —амплитуда колебания — максимальное значение колеблющейся величины;

ω- круговая (циклическая) частота;

φ — начальная фаза колебания в момент времени t=0;

(ωt +φ)— Фаза колебания в момент времени t.

Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до -1, то s может принимать значения от + А до — А .

Поскольку cos(a + 2π) = cosa, то при гармонических колебаниях увеличение (приращение) фазы колебания на 2π приводит к тому, что все величины, характеризующие колебание, принимают исходное значение.

Периодом колебанийT называется наименьший промежуток времени, по истечении которого повторяются состояния колеблющейся системы (совершается одно полное колебание) и фаза колебания получает приращение 2π

ω(t + T) + φ = (ωt + φ ) + 2

Частотой колебанийn называется величина обратная периоду колеба­ний — число полных колебаний, совершаемых в единицу времени

Единица частоты — герц (Гц)— частота периодического процесса, при котором за 1 секунду совершается один цикл колебаний.

3. Дифференциальное уравнение гармонических колебаний.

Первая (скорость) и вторая (ускорение) производные по времени от гармонически колеблющейся величины s также совершают гармонические колебания с той же циклической частотой:

Из последнего уравнения видно, что s удовлетворяет уравнению

или

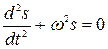
Это уравнение называется дифференциальным уравнением гармони­ческих колебаний. Его решение:

4. Метод векторных диаграмм.

Гармонические колебания изображаются графически методом вращающегося вектора амплитуды или методом векторных диаграмм.

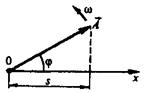
Из произвольной точки О, выбранной на оси х, под углом φ, равным начальной фазе

колебания, откладывается вектор А, модуль которого равен амплитуде А, рассматриваемого колебания. Если этот вектор будет вращаться

вокруг точки О с угловой скоростью со, то проекция вектора на ось х будет совершать колебания по закону s = A·cos(ωt + φ).

5. Экспоненциальная форма записи гармонических колебаний.

Согласно формуле Эйлера для комплексных чисел

где 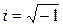— мнимая единица. Поэтому уравнение гармонического колебания s = A·cos(ωt +φ) можно записать в комплексной экспоненциальной форме:

Физический смысл имеет только вещественная часть комплексной функции 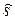, которая и представляет собой гармоническое колебание:

Re( 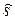) = A cos(ωt +φ) = s

6. Механические гармонические колебания.

Пусть материальная точка совершает прямолинейные гармонические

колебания вдоль оси х около положения равновесия принятого, за начало координат. Тогда для колеблющейся точки

Смещение: х= A·cos(ωt + φ)

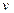
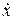
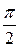
Скорость: = = -Аωcos(ωt + φ + )

Ускорение:

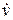
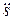
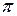
a = = =Аω 2 cos(ωt + φ + )

Амплитуды скорости и ускорения равны Aω и Aω 2

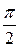
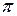
Фаза скорости отличается от фазы смещения на , а фаза ускорения на .

Сила, действующая на колеблющуюся материальную точку массой т равна

Таким образом, сила пропорциональна смещению материальной точки и

направлена в сторону, противоположную смещению (к положению равновесия).

Такая зависимость от смещения характерна для упругих сил и поэтому силы,

которые аналогичным образом зависят от смещения, называются

Квазиупругими.

7. Энергия материальной точки, совершающей гармонические колебания.

Кинетическая энергия материальной точки:

Потенциальная энергия материальной точки, совершающей гармонические колебания под действием квазиупругой силы:

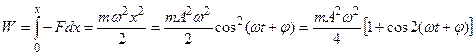
Полная энергия:

остается постоянной, с течением времени происходит только превращение кинетической энергии в потенциальную и обратно.

8. Гармонический осциллятор.

Гармоническим осциллятором называется система, совершающая колебания, описываемые дифференциальным уравнением

Примерами гармонического осциллятора являются пружинный, математический и физический маятники и электрический колебательный контур.

9. Пружинный маятник.

Пружинный маятник — это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы

F =

где 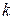— жесткость пружины.

Уравнение движения маятника

или

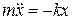
Сравнивая это уравнение с уравнением движения

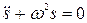
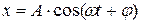
гармонического осциллятора , мы видим, что пружинный маятник совершает колебания по закону с циклической частотой и периодом:

Потенциальная энергия пружинного маятника:

Если на маятник действует сила трения, пропорциональная скорости 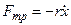,где r — коэффициент сопротивления, то колебания маятника будут

затухающими и закон движения маятника будет иметь вид или

10. Математический маятник.

Математическим маятникомназывается идеализированная система,

состоящая из материальной точки массой т, подвешенной на невесомой нерастяжимой нити длинной l, и колеблющейся под действием силы тяжести без трения.

Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой цлинной нити.

При малых углах отклонения а можно считать: x≈lα.

или

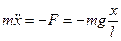
Следовательно, движение математического маятника описывается дифференциальным уравнением гармонических колебаний, то есть происходит по закону х= A·cos(ωt + φ) с частотой и периодом, соответственно:

11 .Физический маятник.

Физическим маятником называется твердое тело, совершающее под действием силы тяжести колебания вокруг горизонтальной оси подвеса, не проходящей через центр масс тела.

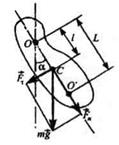Если физический маятник отклонен из положения равновесия на некоторый угол а, то момент возвращающей силы

С другой стороны, при малых углах

где J — момент инерции маятника относительно оси, проходящей через точку подвеса О,

l — расстояние между точкой подвеса и центром масс С маятника,

— возвращающая сила (со знаком минус, поскольку она всегда направленная противоположно направлению увеличения a).

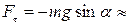
Следовательно: 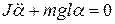, или

Таким образом, при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой и периодом:

где длина 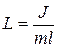— называется приведенной длиной физического ml маятника.

Приведенная длина физического маятника — это длина такого математического маятника, который имеет такой же период колебаний, что и данный физический маятник.

Точка О’ на продолжении прямой ОС, отстоящая от оси подвеса на расстоянии приведенной длины L, называется центром качаний физического маятника.

Математический маятник можно представить как частный (предельный) случай физического маятника, вся масса которого сосредоточена в его центре

масс. При этом J = ml 2 , следовательно .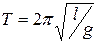

12.Сложение гармонических колебаний.

Если система одновременно участвует в нескольких колебательных процессах, то под сложением колебаний понимают нахождение закона,

описывающего результирующий колебательный

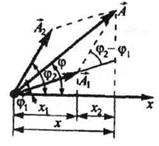
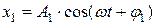
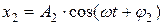
Для сложения колебаний х₁ и х₂ , используем метод вращающегося вектора амплитуды (метод векторных диаграмм).

Так как векторы А₁, и А₂ вращаются с одинаковой угловой скоростью ω, то разность фаз 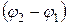между ними остается постоянной. Уравнение результирующего колебания будет

где амплитуда А и начальная фаза φ задаются соотношениями:

Сумма двух гармонических колебаний одного направления и одинаковой частоты есть гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания.

Амплитуда результирующего колебания зависит от разности фаз складываемых колебаний:

1)

2)

13. Биения.

Биениями называются периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами.

Пусть амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω

Дата добавления: 2016-04-22 ; просмотров: 1647 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Свободные колебания.

Свободные колебания (или собственные колебания) — это колебания колебательной системы, совершаемые только благодаря первоначально сообщенной энергии (потенциальной или кинети­ческой) при отсутствии внешних воздействий.

Потенциальная или кинетическая энергия может быть сообщена, например, в механических системах через начальное смещение или начальную скорость.

Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними обра­зуют систему тел, которая называется колебательной системой.

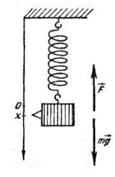
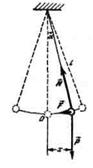
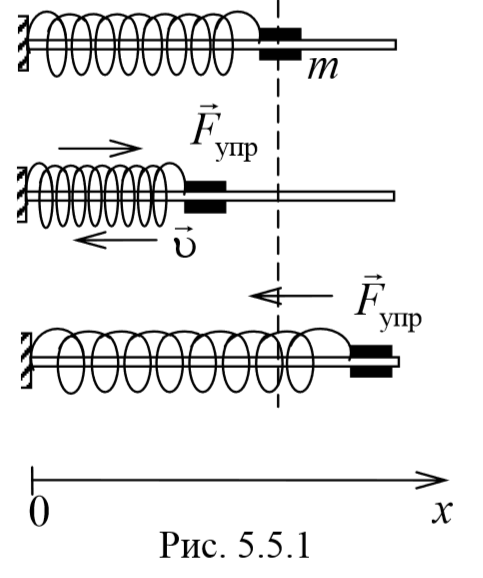
Например, пружина, шарик и вертикальная стойка, к которой прикреплен верхний конец пружины (см. рис. ниже), входят в колебательную систему. Здесь шарик свободно скользит по струне (силы трения пренебрежимо малы). Если отвести шарик вправо и предоставить его самому себе, он будет совершать свободные колебания около положения равновесия (точки О) вследствие действия силы упругости пружины, направленной к положению равновесия.

Другим классическим примером механической колебательной системы является математический маятник (см. рис. ниже). В данном случае шарик совершает свободные колебания под действием двух сил: силы тяжести и силы упругости нити (в колебательную систему входит также Земля). Их равнодействующая направлена к положению равновесия.

Силы, действующие между телами колебательной системы, называются внутренними силами. Внешними силами называют­ся силы, действующие на систему со стороны тел, не входящих в нее. С этой точки зрения свобод­ные колебания можно определить как колебания в системе под действием внутренних сил после того, как система выведена из положения равновесия.

Условиями возникновения свободных колебаний являются:

1) возникновение в них силы, возвращающей систему в положение устойчивого равновесия, после того как ее вывели из этого состояния;

2) отсутствие трения в системе.

Динамика свободных колебаний.

Колебания тела под действием сил упругости. Уравнение колебательного движения тела под действием силы упругости F (см. рис.) может быть получено с учетом второго закона Ньютона (F = mа) и закона Гука (F_упр = -kx), где m — масса шарика, а — ускорение, приобретаемое шариком под действием силы упругости, k — коэффициент жесткости пружины, х — смещение тела от положения равновесия (оба уравнения записаны в проекции на горизонтальную ось Ох). Приравнивая правые части этих уравнений и учитывая, что ускорение а — это вторая производная от координаты х (смещения), получим:

.

Это дифференциальное уравнение движения тела, колеблющегося под действием силы упругости: вторая производная координаты по времени (ускорение тела) прямо пропорциональна его координате, взятой с противоположным знаком.

Колебания математического маятника. Для получения уравнения колебания математического маятника (рисунок) необходимо разложить силу тяжести F_T = mg на нормальную F_n (направлен­ную вдоль нити) и тангенциальную F_τ (касательную к траектории движения шарика — окружности) составляющие. Нормальная составляющая силы тяжести F_n и сила упругости нити F_ynp в сумме сооб­щают маятнику центростремительное ускорение, не влияющее на величину скорости, а лишь меня­ющее ее направление, а тангенциальная составляющая F_τ является той силой, которая возвращает шарик в положение равновесия и заставляет его совершать колебательные движения. Используя, как и в предыдущем случае, закон Ньютона для тангенциального ускорения ma_τ = F_τ и учитывая, что F_τ = -mg sinα, получим:

Знак минус появился потому, что сила и угол отклонения от положения равновесия α име­ют противоположные знаки. Для малых углов отклонения sin α ≈ α. В свою очередь, α = s/l, где s — дуга OA, I — длина нити. Учитывая, что а_τ = s», окончательно получим:

.

Вид уравнения аналогичен уравнению . Только здесь параметрами системы являются длина нити и ускорение свободного падения, а не жесткость пружины и масса шарика; роль координаты играет длина дуги (т. е. пройденный путь, как и в первом случае).

Таким образом, свободные колебания описываются уравнениями одного вида (подчиняются одним и тем же законам) независимо от физической природы сил, вызывающих эти колебания.

Решением уравнений и является функция вида:

То есть координата тела, совершающего свободные колебания, меняется с течением времени по закону косинуса или синуса, и, следовательно, эти колебания являются гармоническими:

В уравнении x = x_m cos ω₀ t (или x = x_m sin ω₀ t), х_m — амплитуда колебания, ω₀ — собственная циклическая (круговая) частота колебаний.

Циклическая частота и период свободных гармонических колебаний определяются свойствами системы. Так, для колебаний тела, прикрепленного к пружине, справедливы соотношения:

.

Собственная частота тем больше, чем больше жесткость пружины или меньше масса груза, что вполне подтверждается опытом.

Для математического маятника выполняются равенства:

.

Эта формула была впервые получена и проверена на опыте голландским ученым Гюйгенсом (современником Ньютона).

Период колебаний возрастает с увеличением длины маятника и не зависит от его массы.

Следует особо обратить внимание на то, что гармонические колебания являются строго периодическими (т. к. подчиняются закону синуса или косинуса) и даже для математического маятни­ка, являющегося идеализацией реального (физического) маятника, возможны только при малых углах колебания. Если углы отклонения велики, смещение груза не будет пропорционально углу отклонения (синусу угла) и ускорение не будет пропорционально смещению.

Скорость и ускорение тела, совершающего свободные колебания, также будут совершать гармонические колебания. Беря производную по времени функции (x = x_m cos ω₀ t (или x = x_m sin ω₀ t)), получим выражение для скорости:

где a_m = ω 2 ₀ x_m — амплитуда ускорения. Таким образом, амплитуда скорости гармонических коле­баний пропорциональна частоте, а амплитуда ускорения — квадрату частоты колебания.

Лекция №7. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

5.1. Свободные гармонические колебания и их характеристики.

Колебания − это движения или процессы, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебания, повторяются через равные промежутки времени. Наиболее важными характеристиками колебания являются: смещение, амплитуда, период, частота, циклическая частота, фаза.

Простейший вид периодических колебаний − это гармонические колебания. Гармонические колебания − это периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса. Уравнение гармонических колебаний имеет вид

1) Смещение x − это величина, характеризующая колебания и равная отклонению тела от положения равновесия в данный момент времени.

2) Амплитуда колебаний А − это величина, равная максимальному отклонению тела от положения равновесия.

3) Период колебаний T − это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Единица измерения [T] = 1 с .

За период система совершает одно полное колебание.

4) Частота колебаний ν − это величина, равная числу колебаний, совершаемых в единицу времени (за 1 секунду). Единица измерения [ν]= 1 Гц . Частота определяется по формуле

5) Циклическая частота ω − это величина, равная числу полных колебаний, совершающихся за 2π секунд. За единицу циклической частоты принята угловая частота, при которой за время 1 с совершается 2π циклов колебаний, [ω]= с -1 . Циклическая частота связана с периодом и частотой колебаний соотношением

6) Фаза колебаний ωt + φ₀ − фаза указывает местоположение колеблющейся точки в данный момент времени.

7) Начальная фаза φ₀ − указывает местоположение колеблющейся точки в момент времени t = 0 .

5.2. Сложение одинаково направленных и взаимно перпендикулярных гармонических колебаний.

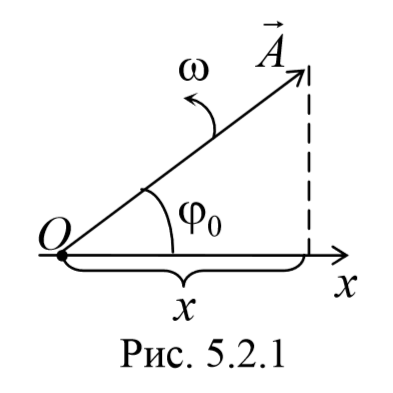
Сложение нескольких колебаний одинакового направления можно изображать графически с помощью метода векторной диаграммы.

Гармоническое колебание может быть представлено графически с помощью вращающегося вектора амплитуды А . Для этого из произвольной точки O , выбранной на оси Ox , под углом φ₀ , равным начальной фазе колебания, откладывается вектор амплитуды А . Модуль этого вектора равен амплитуде рассматриваемого колебания. Если этот вектор привести во вращение с угловой скоростью ω , равной циклической частоте колебаний, то проекция конца вектора амплитуды будет перемещаться по оси Ox и принимать значения от -A до +A , а колеблющаяся величина изменяться со временем по закону x = Acos(ωt + φ₀)

1. Сложение одинаково направленных гармонических колебаний.

Сложим два гармонических колебания одинакового направления и одинаковой частоты. Смещение x колеблющегося тела будет суммой смещений x₁ и x₂ , которые запишутся следующим образом:

Представим оба колебания на векторной диаграмме. Построим по правилу сложения векторов результирующий вектор А . Проекция этого вектора на ось Ox равна сумме проекций слагаемых векторов x=x₂+x₂ , следовательно, вектор А представляет собой результирующее колебание. Определим результирующий вектор амплитуды А потеореме косинусов

Так как угол между векторами А ₁ и А ₂ равен φ=π-(φ₂-φ₁) , то cos[π-(φ₂-φ₁)]=-cos(φ₂-φ₁) , следовательно, результирующая амплитуда колебания будет равна

Определим начальную фазу результирующего колебания.

Из рисунка видно, что начальная фаза результирующего колебания

Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, также совершает гармонические колебания в том же направлении и с той же частотой.

2. Сложение взаимно перпендикулярных гармонических колебаний.

Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты, происходящих во взаимно перпендикулярных направлениях. Допустим, что материальная точка совершает колебания как вдоль оси X , так и вдоль оси Y . Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний примут вид

где φ − разность фаз обоих колебаний.

Уравнение траектории получим, исключив из уравнений (5.2.6) параметр времени t: cosωt= $$x\over A_1$$ , а sinωt= $$\sqrt<1-cos^2 ωt>=\sqrt<1-x^2\over A_1^2>$$ Разложим косинус во втором из уравнений (5.2.6)

Перепишем это уравнение в следующем виде

После преобразования, получим

Используя тригонометрическое тождество cos 2 φ+sin 2 φ=1 , окончательно получим

Это есть уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно. Ориентация эллипса и величина его полуосей зависят от амплитуд колебаний и разности фаз.

Рассмотрим несколько частных случаев и определим форму траектории для них:

a) разность фаз равна нулю [φ=0]

В этом случае $$( < x\over A_1 >— < y\over A_2 >)^2=0$$ , откуда получается уравнение прямой

Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и амплитудой $$A= \sqrt+A_2<^2>>$$ .

2) разность фаз равна ±π[φ=±π] .

В этом случае $$( < x\over A_1 >— < y\over A_2 >)^2=0$$ , откуда получается уравнение прямой

3) Разность фаз равна ± $$π\over 2$$ [φ=± $$π \over2$$ ] . Тогда

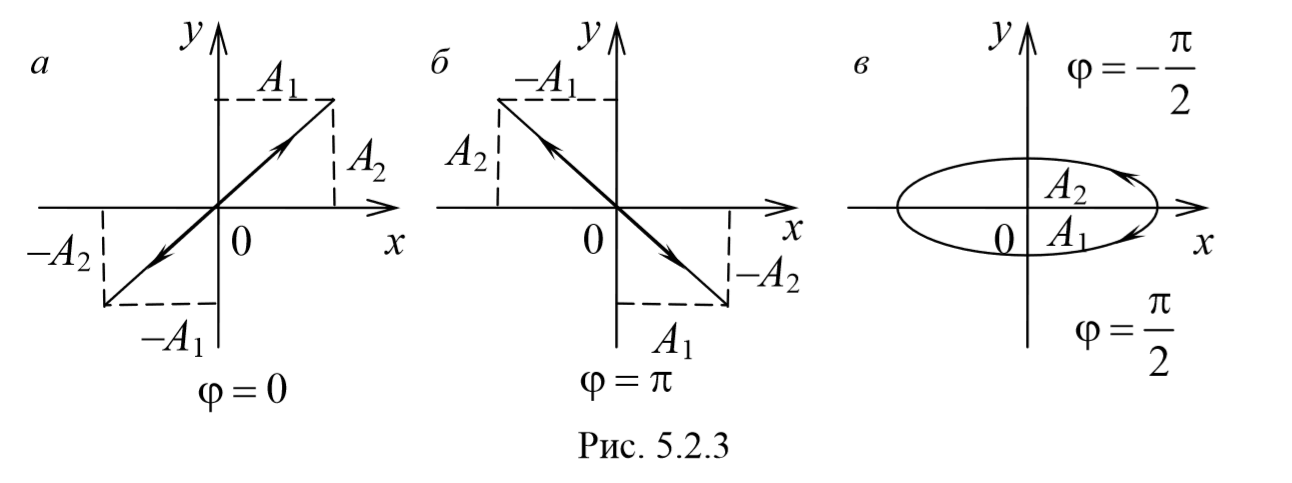
Уравнение эллипса, причем полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд колебаний эллипс вырождается в окружность. Случаи φ=+ $$π\over 2$$ и φ=- $$π\over 2$$ отличаются направлением движения. Если φ=+ $$π\over 2$$ , то уравнения колебаний имеют следующий вид: x=A₁cosωt , и y=-A₂sinωt и движение совершается по часовой стрелке. Если φ=- $$π\over 2$$ , , то уравнения колебаний имеют следующий вид: x=A₁cosωt , и y=A₂sinωt и движение совершается против часовой стрелке.

Рассмотренные три частных случая представлены на рис. 5.2.3, а, б, в. Рис

4) Если частоты складываемых взаимно перпендикулярных колебаний различны, то траектория результирующего движения имеет вид сложных кривых, называемых фигурами Лиссажу . Форма этих кривых определяется соотношением амплитуд, частот и разности фаз складываемых колебаний.

На рис. 5.2.4 показаны фигуры Лиссажу, которые получаются при соотношении частот 1:2 и различной разности фаз колебаний.

По виду фигур можно определить неизвестную частоту по известной частоте или определить соотношение частот складываемых колебаний.

5.3. Дифференциальное уравнение гармонических колебаний и его решение.

Продифференцируем по времени уравнение гармонических колебаний

и получим выражение для скорости

Из сравнения уравнений (5.3.1) и (5.3.2) следует, что скорость опережает смещение по фазе на π/2 . Амплитуда скорости равна Аω .

Продифференцировав уравнение (2) еще раз по времени, получим выражение для ускорения

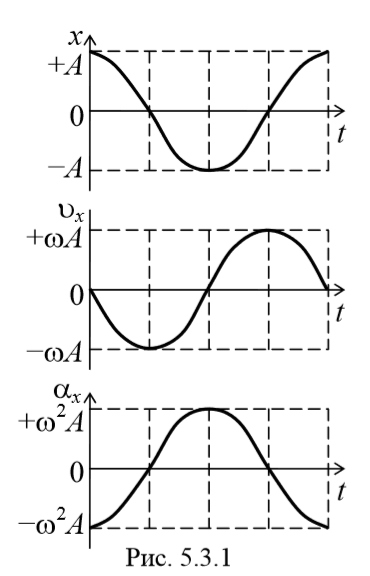
Как следует из уравнения (5.3.3), ускорение и смещение находятся в противофазе. Это означает, что в тот момент времени, когда смещение достигает наибольшего, положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот. Амплитуда ускорения равна Аω 2 (рис. 5.3.1).

Из выражения (5.3.3) следует дифференциальное уравнение гармонических колебаний

Результирующая сила, действующая на материальную точку массой m , определяется с помощью второго закона Ньютона. Проекция этой силы

Эта сила пропорциональна смещению точки из положения равновесия и направлена в сторону противоположную этому смещению, т. е. она стремится вернуть точку в положение равновесия, и поэтому называется возвращающей силой . Таким образом, гармонические колебания происходят под действием силы F , пропорциональной смещению x и направленной к положению равновесия,

где k=mω 2 − постоянный коэффициент. Возвращающая сила подобна упругим силам, возникающим в телах при их деформации. Такая зависимость силы от смещения характерна для упругой силы, поэтому силы иной физической природы, удовлетворяющие зависимости (5.3.6) называются квазиупругими силами .

Материальная точка, совершающая колебания под действием квазиупругой силы, называется линейным осциллятором . Ее динамическое поведение описывается дифференциальным уравнением

ω₀ − собственная частота осциллятора.

Решение этого уравнения дает закон движения линейного осциллятора x=Acos(ωt+φ₀) .

5.4. Энергия гармонических колебаний.

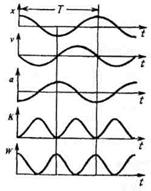
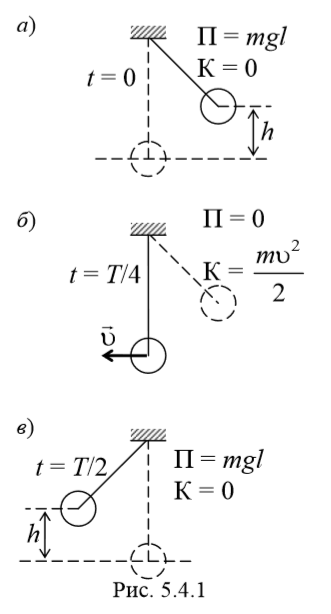
В процессе колебаний происходит превращение кинетической энергии в потенциальную энергию и обратно (рис. 5.4.1). В момент наибольшего отклонения от положения равновесия полная энергия состоит только из потенциальной энергии, которая достигает своего наибольшего значения. Далее при движении к положению равновесия потенциальная энергия уменьшается, при этом кинетическая энергия возрастает. При прохождении через положение равновесия полная энергия состоит лишь из кинетической энергии, которая в этот момент достигает своего наибольшего значения. Далее при движении к точке наибольшего отклонения происходит уменьшение кинетической и увеличение потенциальной энергии. И при наибольшем отклонении потенциальная опять максимальная, а кинетическая энергия рана нулю. И т. д.

Потенциальная энергия тела, совершающего гармонические колебания равна

Кинетическая энергия тела, совершающего гармонические колебания равна

Таким образом, полная энергия гармонического колебания, состоящая из суммы кинетической и потенциальной энергий, определяется следующим образом

Следовательно, полная энергия гармонического колебания

оказывается постоянной в случае гармонических колебаний.

Найдем среднее значение потенциальной энергии за период колебания

Аналогично получается для среднего значение кинетической энергии

Таким образом, и потенциальная, и кинетическая энергии изменяются относительно своих средних значений по гармоническому закону с частотой 2ω и амплитудой ωt kA 2

5.5. Пружинный, математический и физический маятники.

Рассмотрим несколько простейших систем, совершающих свободные гармонические колебания.

1) Пружинный маятник − это материальная точка массой m , подвешенная (или расположенная горизонтально) на абсолютно упругой пружине жесткостью k и совершающий гармонические колебания под действием упругой силы. Пусть шайба массой m , прикрепленная к пружине, совершает колебания. Для составления дифференциального уравнения колебаний запишем второй закон Ньютона в проекции на ось Ox F_упр=ma . Упругая сила F_упр=-kx . Приравнивая последние два уравнения и, используя определение ускорения тела, получим

Сравнивая уравнения (5.3.7) и (5.5.2) получаем, что пружинный маятник совершает гармонические колебания с частотой

Так как период колебаний определяется по формуле T= $$2π\over ω_0$$ , то период колебаний пружинного маятника

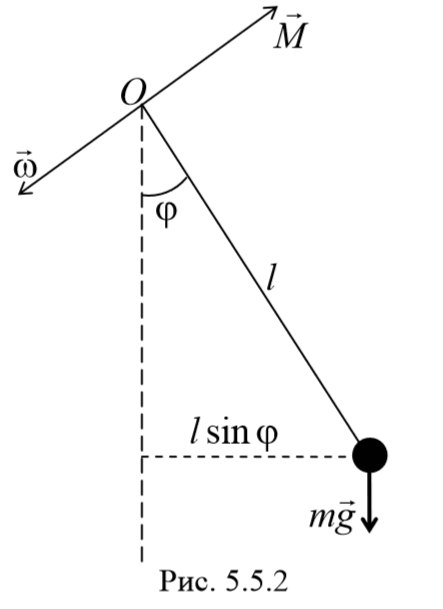
2) Математический маятник − это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена материальная точка массой m . Отклонение маятника от положения равновесия будем характеризовать углом φ , образованным нитью с вертикалью.

При отклонении маятника от положения равновесия возникает вращательный момент M , равный по величине mqlsinφ .Он имее акое же направление, что стремится вернуть маятник в положение равновесия. Следовательно, выражение для вращательного момента имеет вид: M=-mqlsinφ . Применим основно ательного движения

где L=ml 2 − момент инерции материальной точки. Тогда, учитывая, что угловое ускорение ε= $$d^2φ\over dt^2$$ , получим

Если рассматривать малые колебания, то sinφ≈φ . Получим

То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой

Период колебаний математического маятника

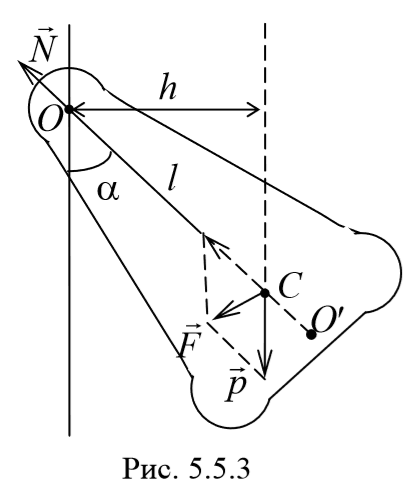
3) Физический маятник − это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, проходящей через точку, не совпадающую с центром масс тела. При отклонении маятника от положения равновесия на угол φ возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен M=-mglsinφ .

Согласно основному уравнению динамики вращательного движения получаем

где I − момент инерции маятника относительно оси, проходящей через точку подвеса.

Если рассматривать малые колебания, то sinφ≈φ . Получим

То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой

Период колебаний математического маятника

Из сопоставления формул периодов колебаний математического и физического маятников T=2π $$\sqrt$$ и T=2π $$\sqrt$$ получается, что математический маятник с длиной

будет иметь такой же период колебаний, что и данный физический маятник.

Величина l_пр (отрезок OO′) называется приведенной длиной физического маятника − это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка на прямой, соединяющей точку подвеса с центром масс, и лежащая на расстоянии приведенной длины от оси вращения, называется центром качания (О′) физического маятника. Точка подвеса О и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.