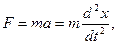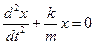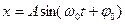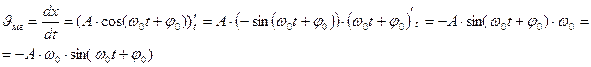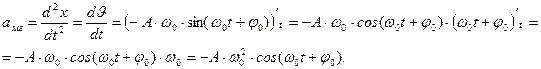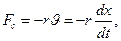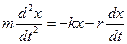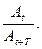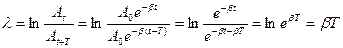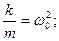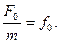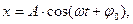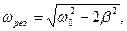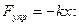Свободные затухающие колебания вывод дифференциального уравнения

Вывод дифференциального уравнения свободного колебания

На тело, совершающее свободные колебания, действуют две силы:

1. Сила, определяемая по второму закону Ньютона:

где m – масса тела;

а – ускорение;

х – смещение;

t – время.

2. Сила упругости, выраженная по закону Гука:

где k – коэффициент упругости. Знак минус показывает, что сила упругости F_упр всегда направлена в сторону положения равновесия.

На основании второго закона Ньютона (произведение массы тела на его ускорение равно сумме всех действующих сил) получаем:

.

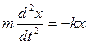
Перенесем –kx в левую часть равенства, получим:

.

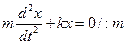
Введем замену: ,

где ω₀ – круговая (циклическая) частота колебаний (ω₀=2πν)

Получили дифференциальное уравнение второго порядка относительно смещения х.

Решением этого уравнения будет:

или (см. рис.1 и рис. 2).

,

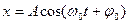
где А – амплитуда колебания;

φ₀ – начальная фаза;

ω₀t+φ₀ – фаза колебания в момент времени t;

ω₀t= ∆φ – изменение фазы колебания за время t.

Выведем уравнения мгновенной скорости и мгновенного ускорения, если колебания совершаются по закону косинуса.

Затухающие колебания.

Все реальные гармонические колебания происходят при воздействии сил сопротивления, на преодоление которых тело затрачивает часть своей энергии, в результате амплитуда колебания уменьшается со временем, т.е. колебания носят затухающий характер.

Представим график затухающего колебания:

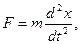
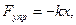
Вывод дифференциального уравнения затухающего колебания.На тело, кроме силы силы упругости действует сила сопротивления:

где r – коэффициент сопротивления.

Согласно второму закону Ньютона можно записать:

.

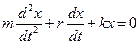
Разделим на массу m, получим:

.

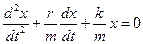
Введем обозначения: ,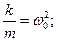

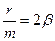
где β – коэффициент затухания.

Получили дифференциальное уравнение затухающего колебания:

.

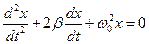
Решение уравнения существенно зависит от знака разности ,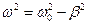

где ω— круговая частота затухающих колебаний, ω₀ — круговая частота собственных колебаний системы (без затухания).

При ω>0 решение дифференциального уравнения будет следующим:

.

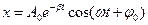
Амплитуда затухающего колебания в любой момент времени t определяется равенством:

,

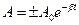
где А₀ – начальная амплитуда, указанная на графике (см. рис 3).

Период Т затухающих колебаний определяется по формуле:

.

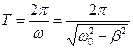
Скорость затухания (быстрота уменьшения амплитуды) определяется величиной коэффициента затухания β: чем больше β, тем быстрее уменьшается амплитуда.

Для характеристики скорости затухания ввели понятие декремента затухания.

Декрементом затухания называется отношение двух соседних амплитуд, разделенных периодом:

На практике степень затухания характеризуется логарифмическим декрементомзатухания λ, равным:

Выведем формулу, связывающую логарифмический декремент затухания λ с коэффициентом затухания β и периодом колебания Т.

.

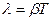
Выведем размерность коэффициента затухания

.

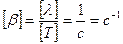
Вынужденные колебания. Вынужденными колебанияминазываются колебания, возникающие в системе при воздействии на неё внешней силы, изменяющейся по периодическому закону.

Пусть на систему действует сила:

где F₀ – максимальное значение,

ω — круговая частота колебаний внешней силы.

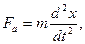
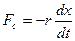
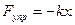
На систему действуют сила сила сопротивления и сила упругости .

С учетом всех четырех сил на основании второго закона Ньютона запишем:

.

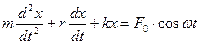
Разделим обе части равенства на m, получим:

.

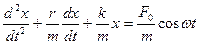
Получили дифференциальное уравнение вынужденного колебания:

.

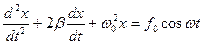
Представим график вынужденных колебаний:

В начале амплитуда колебаний возрастает, а затем становится постоянной А.

Для установившихся вынужденных колебаний:

(см. рис. 4)

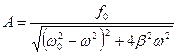
Резонанс.Если ω₀ и β для системы заданы, то амплитуда А вынужденных колебаний имеет максимальное значение при некоторой определенной частоте вынуждающей силы, называемой резонансной. Достижение максимальной амплитуды вынужденных колебаний для заданных ω₀ и β называется резонансом.

Резонансная круговая частота определяется формулой:

а резонансная амплитуда:

.

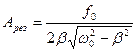
Если отсутствует сопротивление (β=0), то амплитуда неограниченно возрастает.

Представим на графиках зависимость амплитуды вынужденных колебаний от круговой частоты вынуждающей силы ω при различных значениях коэффициента затухания:

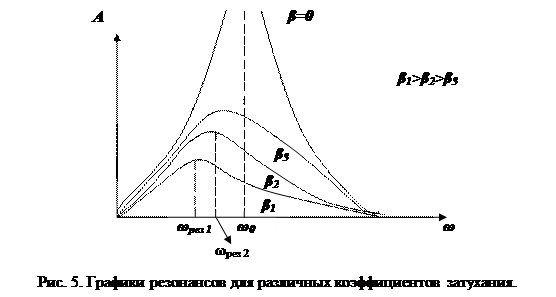По виду резонансной кривой резонанс может быть острым при β→0, тупым – при β→1. (см. рис. 5).

По механизму возбуждения резонанс классифицируется на:

— механический; акустический; электромагнитный; парамагнитный; ядерномагнитный.

Возникновение резонансных явлений в организме может быть как полезным, так и вредным. Например, на акустическом резонансе основано восприятия звука, инфразвук может вызвать разрыв тканей внутренних органов.

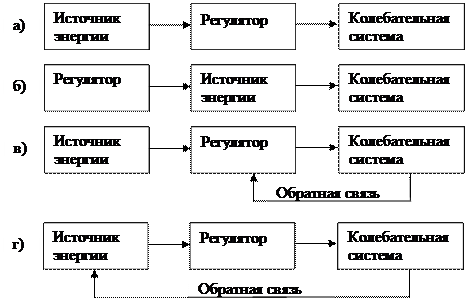
Автоколебания.При затухающих колебаниях энергия системы расходуется на преодоление сопротивления среды. Если восполнять эту потерю энергии, то колебания станут незатухающими. Пополнять эту потерянную системой энергию можно за счет источника энергии извне, а можно сделать так, чтобы колеблющаяся система сама бы управляла внешним воздействием.

Незатухающие колебания, возникающие в системе за счет источника энергии, не обладающего колебательными свойствами, называются автоколебаниями, а сами системы – автоколебательными.

Классическим примером автоколебаний являются часы: заведенная пружина; поднятая гиря – источник энергии; анкер – регулятор поступления энергии от источника; маятник или баланс – колебательная система.

Амплитуда и частота автоколебаний зависят от свойств самой автоколебательной системы.

Автоколебания осуществляется по следующей схеме:

Через канал обратной связи регулятор, получив информацию о состоянии колебательной системы, осуществляет регулирующую подачи энергии от источника к системе.

К автоколебательным системам относятся сердце, легкие и т.д.

Автоколебательная система сердца может быть представлена в следующем виде:

Порядок выполнения работы:

1. Включить кимограф, записать положение равновесия.
2. Отклонив маятник в сторону, отпустить его, одновременно включив секундомер.
3. После записи последнего n-го колебания отключить секундомер.
4. После последнего колебания зарегистрировать положение равновесия и отключить кимограф.
5. Записать графики 3-го – 5-го колебательных процессов.
6. С помощью линейки для каждого графика определить величину начальной амплитуды (А₀) и последней амплитуды (А_n).
7. Подсчитать число полных колебаний на графике (n).
8. Определить период колебания T:

где t – время по секундомеру.

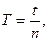
1. Определить величину коэффициента затухания по формуле:

.

1. Определить величину логарифмического декремента затухания: .
2. Полученные данные занести в таблицу.

Контрольные вопросы

1. Определения и единицы измерения основных характеристик колебательного движения.
2. Гармонические колебания. Вывод дифференциального уравнения гармонического колебания и его решение.
3. Затухающие колебания. Вывод дифференциального уравнения затухающего колебания и его решение.
4. Декремент затухания, логарифмический декремент затухания. Вывод формулы, связывающей логарифмический декремент с периодом колебания и коэффициентом затухания.
5. Вынужденные колебания. Дифференциальное уравнение вынужденного колебания и его решение.
6. Резонанс и его значение в медицине.
7. Автоколебания.

Тестовые задания

1. Циклической (круговой) частотой называется число полных колебаний за:

а) 1 с; б) 1 мин; в) 1 ч; г) 2π с.

1. Укажите формулу, связывающую циклическую частоту ω с частотой ν:

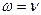
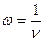
а) ; в) ;

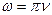
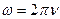
б) ; г) .

1. Укажите формулу, по которой определяется амплитуда затухающего колебания в любой момент времени t:

а) 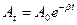; в) ;

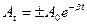
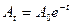
б) . г) .

1. Декрементом затухания называется отношение:

а) двух соседних амплитуд;

б) двух соседних амплитуд, разделенных периодом;

в) первой и последней амплитуд;

г) двух амплитуд, разделенных полупериодом.

1. Укажите единицу измерения коэффициента затухания β:

б) безразмерная величина; г) .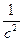

6. Укажите решение дифференциального уравнения свободного гармонического колебания:

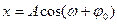
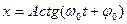
а) ; в) ;

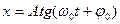
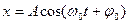
б) ; г) .

7. Укажите, сколько сил действует на систему, если она совершает свободные гармонические колебания:

8. Укажите дифференциальное уравнение свободного гармонического колебания:

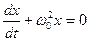
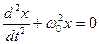
а) ; в) ;

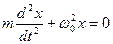
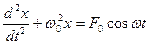
б) ; г) .

9. Укажите решение дифференциального уравнения затухающего колебания:

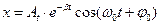
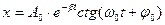
а) ; в) ;

б) 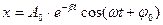; г) .

10. Сколько полных колебаний тело должно совершить в одну минуту, чтобы частота его колебаний равнялась 1 Гц:

11. Укажите подстановку в уравнение смещения затухающего колебания:

:

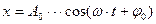
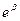
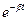
а) ; в) ;

б) ; г) ;

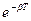
12. Укажите, сколько сил действует на систему, если она совершает вынужденные колебания:

13. Укажите дифференциальное уравнение вынужденного колебания:

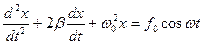
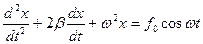
а) ; в) ;

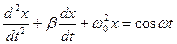
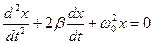
б) ; г) .

14. Укажите блок – схему, по которой осуществляются автоколебания:

15. Укажите формулу, связывающую логарифмический декремент затухания λ с периодом колебания Т и коэффициентом затухания β:

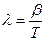
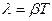
а) ; в) ;

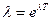
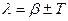
б) ; г) .

16. Укажите дифференциальное уравнение затухающего колебания:

а) ; в) ;

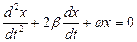
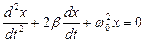
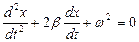
б) ; г) .

17. Укажите, по какой формуле определяется период колебания Т, если за время t тело совершило n полных колебаний:

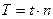
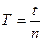
а) ; в) ;

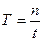
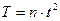
б) ; г) .

18. Укажите единицу измерения логарифмического декремента затухания:

б) с 2 ; г) безразмерная величина.

19. Укажите, какой параметр в уравнении смещения указывает на то, что процесс носит затухающий характер:

20. Укажите, какая сила вызывает уменьшение амплитуды при затухающих колебаниях:

а) ускоряющая сила;

б) сила упругости;

в) сила сопротивления;

г) сила давления.

21. Укажите, при каком значении декремента затухания процесс затухания будет проходить наиболее медленно:

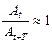
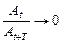
а) ; в) ;

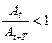
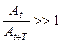
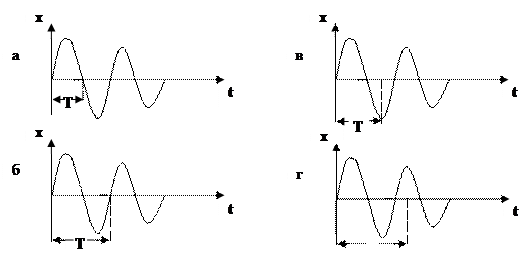
б) ; г) .

22. Укажите, на каком из графиков показан период колебания Т:

23. Укажите график вынужденного колебания:

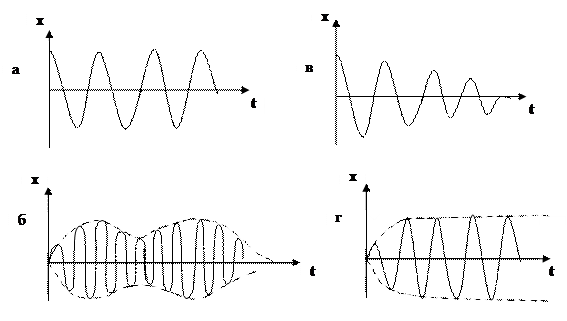24. Укажите, каков физический смысл знака «-» в формуле закона Гука

а) физический смысл отсутствует;

б) показывает, что направления силы упругости F_упр и смещения х совпадают;

в) показывает, что направления силы упругости F_упр и смещения х противоположны;

г) показывает, что направления силы упругости F_упр и смещения х взаимно перпендикулярны.

25. Частотой колебания ν называется величина, показывающая число полных колебаний:

а) за минуту; в) за час;

б) за секунду; г) за сутки.

26. Укажите, в каких единицах измеряется циклическая частота ω:

а) в секундах; в) в минутах;

б) в Гц ; г) в часах.

27. Укажите условие резонанса при β=0:

Свободные затухающие колебания вывод дифференциального уравнения

§6 Затухающие колебания

Декремент затухания. Логарифмический декремент затухания.

Добротность

Свободные колебания технических систем в реальных условиях протекают, когда на них действуют силы сопротивления. Действие этих сил приводит к уменьшению амплитуды колеблющейся величины.

Колебания, амплитуда которых из-за потерь энергии реальной колебательной системы уменьшается с течением времени, называются затухающими.

Наиболее часто встречается случаи, когда сила сопротивления пропорциональна скорости движения

где r — коэффициент сопротивления среды. Знак минус показывает, что F_C направлена в сторону противоположную скорости.

Запишем уравнение колебаний в точке, колеблющийся в среде, коэффициент сопротивлений которой r . По второму закону Ньютона

где β — коэффициент затухания. Этот коэффициент характеризует скорость затухания колебаний, При наличии сил сопротивления энергия колеблющейся системы будет постепенно убывать, колебания будут затухать.

— дифференциальное уравнение затухающих колебаний.

— у равнение затухающих колебаний.

ω – частота затухающих колебаний:

Период затухающих колебаний:

Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно гово­рить, когда β мало.

Если затухания выражены слабо (β→0), то . Затухающие колебания можно

рассматривать как гармонические колебания, амплитуда которых меняется по экспоненциальному закону

В уравнении (1) А₀ и φ₀ — произвольные константы, зависящие от выбора момента времени, начиная е которого мы рассматриваем колебания

Рассмотрим колебание в течение, некоторого времени τ, за которое амплитуда уменьшится в е раз

τ — время релаксации.

Коэффициент затихания β обратно пропорционален времени, в течение которого амплитуда уменьшается в е раз. Однако коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент (по-русски: уменьшение) затухания D , который равен отношению амплитуд, отстоящих по времени на период:

Логарифмический декремент затухания равен логарифму D :

Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний умень­шилась в е раз. Логарифмический декремент затухания — постоянная для данной системы величина.

Еще одной характеристикой колебательной система является добротность Q .

Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ.

Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии.

Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.

Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим.

§7 Вынужденные колебания.

Резонанс

В целом ряде случаев возникает необходимость создания систем, совершающих незатухающие колебания. Получить незатухающие колебания в системе можно, если компенсировать потери энергии, воздействуя на систему периодически изменяющейся силой.

Запишем выражение для уравнения движения материальной точки, совершающей гармоническое колебательное движение под действием вынуждающей силы.

По второму закону Ньютона:

(1)

— дифференциальное уравнение вынуж­денных колебаний.

Это дифференциальное уравнение является линейным неоднородным.

Его решение равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения:

Найдем частное решение неоднородного уравнения. Для этого перепишем уравнение (1) в следующем виде:

(2)

Частное решение этого уравнения будем искать в виде:

т.к. выполняется для любого t , то должно выполняться равенство γ = ω , следовательно,

Это комплексное число удобно представить в виде

где А определяется по формуле (3 ниже), а φ — по формуле (4), следовательно, решение (2),в комплексной форме имеет вид

Его вещественная часть, являвшаяся решением уравнения (1) равна:

(3)

(4)

Слагаемое Х_о.о. играет существенную роль только в начальной стадии при установлении колебаний до тех пор, пока амплитуда вынужденных колебаний не достигнет значения определяемого равенством (3). В установившемся режиме вынужденные колебания происходят с частотой ω и являются гармоническими. Амплитуда (3) и фаза (4) вынужденных колебаний зависят от частоты вынуждающей силы. При определенной частоте вынуждающей силы амплитуда может достигнуть очень больших значений. Резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте механи­ческой системы, называется резонансом.

Частота ω вынуждающей силы, при которой наблюдается резонанс, называется резонансной. Для того чтобы найти значение ω_рез, необходимо найти условие максимума амплитуды. Для этого нужно определить условие минимума знаменателя в (3) (т.е. исследовать (3) на экстремум).

Зависимость амплитуды колеблющейся величины от частоты вынуждающей силы называется резонансной кривой. Резонансная кривая будет тем выше, чем меньше коэффициент затухания β и с уменьшением β, максимум резонансных кривых смешается вправо. Если β = 0, то

При ω→0 все кривые приходят к значению — статическое отклонение.

Параметрический резонанс возникает в том случае, когда периодическое изменение одного из параметров система приводит к резкому увеличению амплитуды колеблющейся системы. Например, кабины, делающие «солнышко» за счет изменения положения центра тяжести система.(То же в «лодочках».) См. §61 .т. 1 Савельев И.В.

Дифференциальное уравнение свободных затухающих колебаний (механических и электромагнитных) и его решение. Автоколебания

Рассмотрим свободные затухающие коле­бания— колебания, амплитуда которых из-за потерь энергии реальной колебатель­ной системой с течением времени умень­шается. Простейшим механизмом умень­шения энергии колебаний является ее пре­вращение в теплоту вследствие трения в механических колебательных системах,

а также омических потерь и излучения электромагнитной энергии в электриче­ских колебательных системах.

Закон затухающих колебаний опреде­ляется свойствами колебательных систем. Обычно рассматривают линейные систе­мы— идеализированные реальные систе­мы, в которых параметры, определяющие физические свойства системы, в ходе про­цесса не изменяются. Линейными система­ми являются, например, пружинный маят­ник при малых растяжениях пружины (когда справедлив закон Гука), колеба­тельный контур, индуктивность, емкость и сопротивление которого не зависят ни от тока в контуре, ни от напряжения. Различ­ные по своей природе линейные системы описываются идентичными линейными дифференциальными уравнениями, что по­зволяет подходить к изучению колебаний различной физической природы с единой точки зрения, а также проводить их моде­лирование, в том числе и на ЭВМ.

Дифференциальное уравнение свобод­ных затухающих колебанийлинейной системы задается в виде

где s — колеблющаяся величина, описы­вающая тот или иной физический про­цесс, d=const — коэффициент затухания,w₀ — циклическая частота свободных не­затухающих колебаний той же колебатель­ной системы, т. е. при d=0 (при отсутствии потерь энергии) называется собственной частотойколебательной системы.

Решение уравнения (146.1) рассмот­рим в виде

где u=u(t). После нахождения первой и второй производных выражения (146.2) и подстановки их в (146.1) получим

Решение уравнения (146.3) зависит от знака коэффициента перед искомой вели­чиной. Рассмотрим случай, когда этот ко­эффициент положителен:

w 2 =w 2 ₀-d 2 (146.4)

(если (w 2 -d 2 )>0, то такое обозначение мы вправе сделать). Тогда получим урав­нение типа (142.1)

решением которого является функция и=А₀cos(wt+j)

Таким образом, решение уравнения (146.1) в случае малых затуханий (d 2 2 ₀)

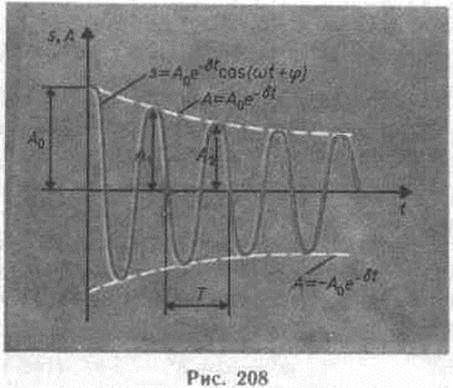
— амплитуда затухающих колебаний,а

a₀— начальная амплитуда. Зависимость (146.5) показана на рис.208 сплошной линией, а зависимость (146.6) — штри­ховыми линиями. Промежуток времени t=1/d, в течение которого амплитуда за­тухающих колебаний уменьшается в е раз, называется временем релаксации.

Затухание нарушает периодичность колебаний, поэтому затухающие колеба­ния не являются периодическими и, строго говоря, к ним неприменимо понятие перио­да или частоты. Однако если затухание мало, то можно условно пользоваться по­нятием периода как промежутка времени между двумя последующими максимума­ми (или минимумами) колеблющейся фи­зической величины (рис. 208). Тогда пери­од затухающих колебаний с учетом формулы

Если A(t) и A(t+T)— амплитуды двух последовательных колебаний, соответству­ющих моментам времени, отличающимся на период, то отношение

называется декрементом затухания, а его

— логарифмическим декрементом затуха­ния;N_e — число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания — постоянная для данной колебательной системы величина.

Для характеристики колебательной системы пользуются понятием добротно­стиQ, которая при малых значениях лога­рифмического декремента равна

(так как затухание невелико (d 2 2 ₀), то Т принято равным Т₀).

Из формулы (146.8) следует, что до­бротность пропорциональна числу колеба­ний N_e, совершаемых системой за время релаксации.

Применим выводы, полученные для свободных затухающих колебаний линей­ных систем, для колебаний различной фи­зической природы — механических (в ка­честве примера рассмотрим пружинный маятник) и электромагнитных (в качестве примера рассмотрим электрический коле­бательный контур).

1. Свободные затухающие колебания пружинного маятника.Для пружинного маятника (см. § 142) массой т, совершаю­щего малые колебания под действием уп­ругой силы F=-kx, сила трения про­порциональна скорости, т. е.

где r — коэффициент сопротивления;знак минус указывает на противоположные на­правления силы трения и скорости.

При данных условиях закон движения маятника будет иметь вид

Используя формулу w₀=Ök/m (см. (142.2)) и принимая, что коэффици­ент затухания

получим идентичное уравнению (146.1) дифференциальное уравнение затухающих колебаний, маятника:

Из выражений (146.1) и (146.5) вытекает, что маятник колеблется по закону

х=A₀е — d t cos(wt+j) с частотой w=Ö(w 2 ₀-r2/4m 2 ) (см. (146.4)).

Добротность пружинного маятника,

согласно (146.8) и (146.10), Q=1/rÖkm.