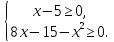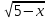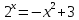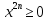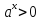Свойства функции 9 класс как решать уравнения

Применение свойств функций для решения уравнений

В работе рассматриваются сособы решения уравнений с использованием свойств и характеристик функций: монотонности, ограниченности, области определенийи области значений функции.

Просмотр содержимого документа
«Применение свойств функций для решения уравнений»

II. Применение свойств функций для решения уравнений

Использование ОДЗ для решения уравнений .………….. 2стр

Монотонность функции и наличие корней уравнении…. 3стр

Используемая литература………………………………………. 10 стр

Найти и освоить приемы решения уравнений способами, позволяющими значительно сократить время нахождения корней уравнений.

В ходе сбора и изучения информации по данной теме, были найдены и изучены рациональные приемы решения уравнений с применением свойств монотонности, ограниченности функций, а также области определения и значений функций, позволяющие эффективно (практически устно) решать некоторые виды уравнений, рассмотренных в качестве примеров в нашей работе.

В наших школьных учебниках алгебры в основном изучаются такие методы и приемы решения уравнений как возведение в степень, замена переменной, применение тождественных преобразований, Но использование этих способов при решении некоторых видов уравнений приводит к довольно долгим и сложным преобразованиям, особенно если уравнения в левой и правой части которой находятся функции, имеющие различную природу.

В ходе наших поисков мы познакомились с одним из эффективных способов решения уравнений вида f(x)=g(x), который и демонстрируем в нашей работе. Это способ решения уравнений с использованием свойств функций.

Начнем с уравнений, которые можно решить, используя область определения функции или область допустимых значений переменной. Напомним, что множество значений переменной, при которых обе части данного уравнения (или неравенства) имеют смысл называют областью допустимых значений уравнения или неравенства. Рассмотрим такие уравнения, которые можно решить просто найдя ОДЗ.

​​​ = 3−x

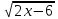
Пусть f(x) = 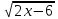. Тогда D (f) определяется неравенством 2х – 6≥ 0, т.е. x≥3, а E(f) = [0; +∞ )

Значит правая часть уравнения должна быть неотрицательной, т.е. должно выполнятся условие 3−x ≥ 0, тогда x ≤ 3. Определяется системой двух неравенств: x≥3 и x ≤ 3. Получаем, что ОДЗ уравнения: х=3.Легко видеть, что 3 будет корнем исходного уравнения.

Приведем еще один пример уравнения:

​​+​ ​​​= 27x−15

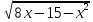
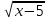
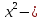
Решение: Найдем ОДЗ, решив систему неравенств

Решая неравенства этой системы получим 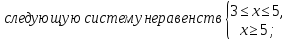А эта система имеет решение х=5. Таким образом, уравнение имеет смысл только при одном значении переменной. Подставив x=5 в уравнение, убеждаемся, что получаем верное равенство. Значит 5 – корень данного уравнения.

Монотонность функции и наличие корней уравнения.

Рассмотрим как применяются такое свойство функции как монотонность. Для успешного решения уравнения этим способом необходимо знать следующие утверждения: 1) если функция f (х) на некотором промежутке возрастает, а функция g(х) убывает на этом же промежутке, то уравнение f(х) = g(х) имеет на этом промежутке не более одного корня; 2) Если на некотором промежутке функция f(x) возрастает (или убывает), то уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — постоянная величина (число)). Применение свойства продемонстрируем на следующих примерах:

1) x 1991 +1 =

1) В левой части этого уравнения стоит возрастающая функция на на R
в правой – убывающая на (-∞;5].
Если уравнение и будет иметь корень, то только на промежутке (-∞;5]. Легко заметить, что этот корень 1, и он, согласно теореме, единственный.

2) 5x 19 + 4x 3 +3х=12. Функция, стоящая в левой части уравнения является возрастающей (как сумма возрастающих функций). Следовательно, уравнение имеет не более одного корня. Подбором находим, что x=1.

3) +=2. Областью определения функции, стоящей в левой части, является промежуток [-1; ∞). На этом промежутке функция возрастает. Следовательно, корень, равный -1 – единственный.

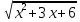
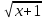
4) 2 x 15 + 3x=5/х. Функция f(x) = 5/х на каждом из промежутков (-∞;0) и (0:∞) убывает, а функция g (х) = 2 x 15 + 3x возрастает на каждом из них, поэтому наше уравнение на каждом из этих промежутков имеет не более одного корня. Убеждаемся, что это числа 1 и -1.

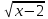
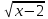
5) 2= 9/х – 1.Функция f(x)= 2 на промежутке [ 2; ∞) возрастает, а функция g (х) = 9/х – 1 на этом же промежутке убывает, значит уравнение имеет не более одного корня на этом промежутке. И этот корень равен 3.

6) найти положительные корни уравнения

Функция 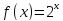возрастает на R. g (х)=
Убывает на промежутке [ 0; ∞). Следовательно, на промежутке [ 0; ∞) уравнение имеет не более одного корня. Подбором находим что х =1.

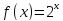
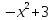
Функция возрастает на(0; ∞) . а функция g (х)= на этом промежутке убывает. Значит, уравнение будет иметь корни только на промежутке (0; ∞). Подбором находим корень уравнения –это число 2.

Рассмотрим, как можно применить к решению уравнений такое свойство функции как ограниченность. Метод, с помощью которого решаются уравнения с применением ограниченности функции, получил название метода мажорант. Ну, а само название метода происходит от французского слова majorer — объявлять большим. Мажорантой данной функции f(х) на множестве Р, называется такое число М, что либо f(х) ≤ М для всех х ϵ Р, либо f(х) ≥ М для всех х ϵ Р. Основная идея метода состоит в следующем: Пусть имеется уравнение f(х) = g(х) и существует такое такое число М, что для любого х из области определения f(х) и g(х) имеем f(х) ≤ М и g(х) ≥ М. Тогда уравнение f(х) = g(х) равносильно системе 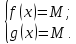Метод применим к уравнениям, в которых используются ограниченные фукции, т. е. функции, множество значений которых ограниченно. Вот некоторые из них:

1. -1≤sinx≤1 или ≤1

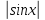
2. -1≤cosx≤1 или 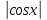≤1

3.

4.

5.

6.

Применение метода рассмотрим на следующих примерах.

1) Решим уравнение: + =0.

4и 10 степени – это четные числа, значит и при любом значении x. Тогда наше уравнение будет равносильно системе уравненийПервое уравнение имеет единственный корень – это число3, значит, если система и будет иметь решение, то не более одного. Проверкой убеждаемся, что3 является корнем и второго уравнения системы, а следовательно и исходного уравнения.

Заменим левую часть уравнения логарифмом, используя свойство разности логарифмов:

Представим дробь в виде , и используя неравенство Коши оценим подлогарифмическое выражение. Получаем (x + ) ≥ 4, а значит

log₂ (x + ) ≥ 2. Таким образом, левая часть уравнения не меньше 2.

Рассмотрим правую часть уравнения. В правой части содержится квадратный трехчлен, поэтому выделив из него квадрат двучлена приходим к выводу, что данное выражение принимает значения не больше 2:

4 x – x 2 – 2 = – x 2 + 4 x – 2 = – ( – 4 x + 4 – 2) = – (x — 2) 2 + 2 = 2 – ( x — 2) 2

Получили, что правая часть уравнения не больше 2, т.к. (x — 2) 2 ≥ 0 при любых х. Значит, равенство левой и правой частей уравнения достигается, если они одновременно равны 2.

Из первого уравнения системы находим корень х = 2. Убеждаемся, что этот корень удовлетворяет и второму уравнению системы. Следовательно, решением исходного уравнения будет х = 2.

3) Решить уравнение:

В левой части уравнения стоит тригонометрическая функция, а в правой – сумма показательных. Формул, позволяющих находить корни в таких случаях, не существует. Оценим каждую из частей уравнения. Очевидно, что левая часть уравнения не больше 2. И так как

Поскольку 0, то причем равенство достигается только при x = 0. В данном случае

Получили, что левая часть уравнения не больше двух, а правая часть – больше или равняется двум. Таким образом, уравнение имеет решение, только если имеет решение система уравнений:

Проверкой убеждаемся, что x=0 – корень уравнения: . Значит число 0 – корень исходного уравнения. Получили ответ: x = 0.

Рассмотрим решение еще одного уравнения:

Рассмотрим две функции

Уравнение имеет решение, если наибольшее значение функции f(х) равно наименьшему значению функции g(х). Таким образом, уравнение имеет решение, только если обе части равны 2. И наше уравнение равносильно системе:

Решим первое уравнение системы:

Подставив данный корень во второе уравнение системы, получим верное равенство. Значит, решением исходного уравнения будут числа вида .

Функция y= (квадратичная функция) имеет наименьшее значение при , равное y(2)=4

Функция у= является возрастающей и, следовательно, принимает наименьшее значение при x=2

Правая часть уравнения, в силу ограниченности функции принимает значения не больше 2, поэтому исходное уравнение равносильно системе:

Так как 2-корень первого уравнения, то убедимся, что число 2-корень второго уравнения. Получаем:

Таким образом, 2-корень исходного уравнения.

Рассмотренные нами примеры могли быть решены и другими методами, но традиционные методы в данных конкретных примерах достаточно трудоемки. В нашей работе мы постарались продемонстрировать применение некоторых нестандартных приемов решения уравнений, основанных на свойствах и характеристиках функций. Планируем продолжить изучение нетрадиционных и эффективных приемов решения уравнений.

Основные свойства числовых функций

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Важными характеристиками конкретных функций являются область определения и область значения. На уроке будут рассматриваться задачи на нахождение области определения, области значения функции, сопутствующие задачи, включая задачи с параметрами.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Функции»

Урок алгебры в 9-м классе «Свойства функций»

Презентация к уроку

Загрузить презентацию (206 кБ)

Тип урока: изучение нового материала.

Цели урока:

• Образовательная – рассмотреть основные свойства числовых функций и проиллюстрируя их графически; дать им более точные определения.
• Развивающая – развитие логического мышления, анализа, памяти.
• Воспитательная – воспитание уверенности, внимания.

Оборудование: компьютер, проектор, презентация.

Актуальность:

• задания по данной теме встречаются в ГИА по математике в 9 классе и в ЕГЭ — 11 класса;
• чтение графиков функций имеет большое практическое значение.

Ход урока

1. Оргмомент.

2. Сообщение темы и целей урока.

3. Объяснение нового материала.

Любая функция характеризуется определенными свойствами. Часть этих свойств было рассмотрено в 7 – 8 классах. Теперь необходимо систематизировать эти свойства и использовать их при построении и исследовании конкретных функций.

На этом уроке мы рассмотрим основные свойства числовых функций и проиллюстрируем их графически. К основным свойствам функции относятся ее область определения и область значений, ограниченность функции сверху или снизу, наименьшее и наибольшее значение функции, возрастание и убывание функции, а также понятие монотонности и непрерывности. Дадим определения основных свойств, а также решим ряд примеров на чтение графика функции.

• Какие свойства функций вам знакомы из курса алгебры 7 – 8 классов?
• Дадим более точные определения перечисленным свойствам функций и закрепим их при чтении графиков. (Презентация)

1. Область определения и область значения функции.

Пусть числовые множества Х и У. Если указано правило f, позволяющее поставить в соответствии каждому элементу х из Х определенный элемент у из множества У, то говорят, что задана функция y = f(x) c областью определения Х и областью значений У.

Для области определения функции y = f(x) принято обозначение D(f), для области значений – обозначение E(f). (Слайд 2)

Пример на нахождение области определения и области значений функции. (Слайд 3, 4)

2. Монотонность функции.

Рассмотрим еще одно свойство функции – монотонность (т. е. возрастание или убывание функции).

Определение 1. Функцию y = f(x) называют возрастающей на множестве , если для любых двух элементов х₁ и х₂ множества Х, таких что х₁ f(х₂). (Слайд 5)

Пример на нахождение промежутков возрастания и убывания функции. (Слайд 8)

Определение 3. Функцию y = f(x) называют ограниченной снизу на множестве , если существует число m такое, что для любого значения х из множества Х выполняется неравенство f(x)>m.

Определение 4. Функцию y = f(x) называют ограниченной сверху на множестве , если существует число М такое, что для любого значения х из множества Х выполняется неравенство f(x) 2 .

3 группа: функция у = к/х.

4 группа: функция у =

5 группа: функция у =

6 группа: функция у = ах 2 + bx + c.

5. Выступление у доски.

6. Задание из учебного пособия: № 10.14

7. Итог урока.

Одно задание для всех групп. (Слайд18) Каждая группа самостоятельно читает график функции изображенный на слайде. Затем меняются ответами и проверяют. Один учащийся (по желанию) у доски читает этот график. Если есть ошибки, то они исправляются по ходу чтения графика.

8. Домашнее задание. §8, 10 – читать, учить; № 10.16. (Домашнее задание подробно объяснить по книге)

Литература:

1. А.Г. Мордкович, П.В. Семенов, Алгебра, Часть 1, Учебник 9 класс.
2. А.Г. Мордкович, П.В. Семенов, Алгебра, Часть 2, Задачник 9 класс.
3. Сборник тестовых заданий, Алгебра 9, Лаборатория аттестационных технологий, Московский институт повышения квалификации работников образования.