Свойства ранга матрицы системы линейных уравнений

Исследование СЛАУ. Общие сведения

В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.

Общие сведения (определения, условия, методы, виды)

Системы линейных алгебраических уравнений с n неизвестными могут иметь:

• единственное решение;
• бесконечное множество решение (неопределенные СЛАУ);
• ни одного решения (несовместные СЛАУ).

Пример 1

Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.

Система x + y = 1 2 x + 7 y = — 3 имеет единственное решение x = 2 ; y = 1 .

Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 — t при — ∞ t ∞ .

Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:

• Совместна ли система?
• Если система совместна, то, какое количество решений она имеет — одно или несколько?
• Как найти все решения?

Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:

• если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
• если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
• если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.

Ранг матрицы и его свойства

Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.

Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда

В математике выделяют следующие подходы к определению ранга матрицы:

• при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
• при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
• при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.

Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .

Свойства ранга матрицы:

1. квадратная невырожденная матрица обладает рангом, который отличается от нуля;
2. если транспонировать матрицу, то ранг матрицы не изменяется;
3. если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
4. при удалении нулевого столбца или строки ранг матрицы не изменяется;
5. ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
6. при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
7. ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
8. когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .

Пример 2

А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0

r ( A 1 ) = 1 , r ( B 1 ) = 1

А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6

Ранг матрицы

Рассмотрим матрицу размером m х n

Выберем в ней произвольно s разных строк и s столбцов, причем 1 то, взяв первую и третью строку, третий и пятый столбец, получим матрицу второго порядка и ее определитель

Этот определитель является минором второго порядка для исходной матрицы. Аналогично можно получить остальные миноры второго порядка и третьего порядка. Некоторые из миноров могут оказаться равными нулю.

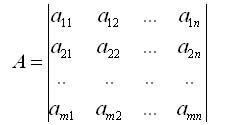
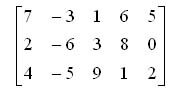
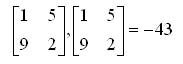
Ранг матрицы — наибольший из порядков ее миноров не равных нулю. Ранг матрицы А обозначают одним из символов: rang А, r. Если все миноры матрицы равны нулю, то ранг ее считается равным нулю.

Из определения ранга матрицы получаем следующие утверждения:

1. Ранг матрицы определяется целым числом, заключенным между 0 и меньшим из чисел m, n.
2. Ранг матрицы равен нулю, если матрица нулевая.
3. Для квадратной матрицы n-го порядка r = п тогда и только тогда, когда матрица невырожденная.

При нахождении ранга матрицы можно пользоваться свойствами миноров. Если все миноры определенного порядка матрицы равны нулю, то все миноры более высокого порядка также равны нулю. Таким образом, если среди миноров порядка k данной матрицы есть отличные от нуля, а всё миноры порядка k + 1 равны нулю или не существуют, то r= k.

Свойства ранга матрицы

1. Ранг матрицы, полученной транспонированием, равен рангу исходной матрицы.

2. Ранг матрицы останется неизменным, если вычеркнуть или приписать нулевую строку (т. е. строку, все элементы которой равны нулю) или нулевой столбец.

При элементарных преобразованиях ранг матрицы не меняется. С помощью элементарных преобразований матрицу можно привести к квазитреугольной форме. Ранг квазитреугольной матрицы равен r, поскольку ее минор с главной диагональю а11а22,…,аnn равен произведению не равным нулю а все миноры более высокого порядка равны нулю (как содержащие нулевые строки).

Для решения контрольной по математике на нахождения ранга жмите сюда.

Ранг матрицы

Определение ранга матрицы.

Пусть в матрице A существует линейно независимая система из r строк, и нет линейно независимой системы из большего числа строк. Тогда мы будем говорить, что строчный ранг матрицы A равен r . Нулевая матрица не содержит никакой линейно независимой системы строк, и ее строчный ранг по определению равен нулю.

Аналогично определяется столбцовый ранг матрицы. Он равен r_ <1>, если есть линейно независимая система из r_ <1>столбцов, и нет линейно независимой системы из большего числа столбцов. Столбцовый ранг нулевой матрицы по определению равен нулю.

Система из r строк линейно независима тогда и только тогда, когда в этих строках найдется невырожденная подматрица порядка r .

1^ <\circ>. Пусть r строк линейно зависимы. Рассмотрим произвольную подматрицу порядка r , расположенную в этих строках. Если строки линейно зависимы, то также линейно зависимы (с теми же коэффициентами) и отрезки этих строк, составляющие подматрицу, и подматрица является вырожденной.

2^ <\circ>. Обратное утверждение докажем по индукции. Одна строка линейно независима, если она не нулевая. В этом случае она содержит ненулевой элемент, составляющий невырожденную подматрицу порядка 1.

Пусть теперь даны r линейно независимых строк. Первые r-1 из них также линейно независимы, и по предположению индукции содержат невырожденную подматрицу порядка r-1 . Пусть j_<1>. j_ — номера столбцов этой подматрицы. Рассмотрим отрезок r -й строки, расположенный под подматрицей, то есть составленный из элементов с номерами j_<1>. j_ . По следствию из ранее доказанной теоремы этот отрезок раскладывается в линейную комбинацию строк подматрицы. Коэффициенты этой линейной комбинации обозначим \alpha_<1>. \alpha_ .

Теперь будем рассматривать полные строки. Вычтем из последней строки линейную комбинацию предыдущих с теми же коэффициентами \alpha_<1>. \alpha_ . Это обратит в нуль j_<1>. j_ -й элементы r -й строки, но не всю строку, так как строки линейно независимы. Таким образом, в преобразованной r -й строке есть ненулевой элемент a_^ , и его номер j отличен от номеров j_<1>. j_ .

Невырождена соответствующая подматрица и в непреобразованной матрице, так как элементарными преобразованиями мы превратили ее в невырожденную матрицу. Это заканчивает доказательство.

В матрице A размеров m \times n подматрица порядка r называется базисной, если она невырождена, а все квадратные подматрицы большего порядка, если они существуют, вырождены.

Столбцы и строки матрицы A , на пересечении которых стоит базисная подматрица, называются базисными столбцами и строками A .

В силу утверждения 1 базисные столбцы и строки линейно независимы.

Рангом матрицы называется порядок базисной подматрицы или, иначе, самый большой порядок, для которого существуют невырожденные подматрицы. Ранг нулевой матрицы по определению считают нулем.

Отметим два очевидных свойства ранга.

Основные теоремы.

Из утверждения 1 прямо следует теорема о ранге матрицы:

Таким образом, мы видим, что все три определения на самом деле определяют одно и то же число, и впредь не будем их различать. Будем говорить ранг матрицы и обозначать его \mathbf\,A .

Из теоремы о ранге матрицы мы получаем теорему о базисном миноре, на которую существенно опирается все дальнейшее изложение. Слово “минор” означает “детерминант подматрицы”. В частности, базисный минор — это детерминант базисной подматрицы. О детерминантах будет речь в следующем параграфе, а здесь это слово можно воспринимать просто как составную часть названия теоремы.

Каждый из базисных столбцов, разумеется, раскладывается по базисным: для этого достаточно взять его самого с коэффициентом 1, а остальные с нулевыми коэффициентами.

Ранг произведения матриц.

Согласно ранее доказанным утверждениям элементарные преобразования не меняют столбцового ранга. Таким образом, справедливо

Ранг матрицы не меняется при элементарных преобразованиях.

Если матрица A невырождена и определены произведения AB и CA , то \mathbf\,AB=\mathbf\,B и \mathbf\,CA=\mathbf\,C .

В общем случае имеет место

Ранг произведения двух матриц не превосходит рангов сомножителей.

Пусть определено произведение AB . Рассмотрим матрицу D , составленную из всех столбцов матриц A и AB . Так как AB — подматрица, \mathbf\,AB \leq \mathbf\,D .

По утверждению о том, что столбцы AB — линейные комбинации столбцов A . Легко видеть, что приписывание к матрице линейной комбинации ее столбцов не меняет ранга матрицы. Действительно, не меняя ранга, элементарными преобразованиями столбцов мы можем обратить приписанный столбец в нулевой, а добавление нулевого столбца не создает новых невырожденных подматриц. Отсюда следует, что \mathbf\,D=\mathbf\,A . Итак, \mathbf\,AB \leq\mathbf\,A .

Аналогично доказывается, что \mathbf\,AB \leq\mathbf\,B . Для этого надо составить матрицу D’ из всех строк матриц B и AB .

Нахождение ранга матрицы.

Матрица размеров m \times n называется упрощенной (или имеет упрощенный вид), если некоторые r ее столбцов являются первыми r столбцами единичной матрицы порядка m и, в случае m > r , ее последние (m-r) строк — нулевые.

Каждую матрицу с помощью элементарных преобразований строк можно превратить в упрощенную матрицу.

Если матрица нулевая, то она уже упрощенная (r=0) . В общем случае применим метод Гаусса. В ранее доказанном утверждении мы превратили квадратную невырожденную матрицу элементарными преобразованиями строк в единичную матрицу. Это — частный случай доказываемого утверждения. То обстоятельство, что матрица невырождена, использовалось, когда мы в очередной строке преобразованной матрицы находили ненулевой элемент.

В общем случае ненулевой элемент может не найтись, то есть очередная строка окажется нулевой. Все встречающиеся нулевые строки будем переставлять на последние места и будем продолжать преобразования так, как при доказательстве утверждения, на которое ссылались выше.

Преобразования закончатся, когда либо будут исчерпаны все строки, либо останутся только нулевые строки. При этом не существенно, квадратная матрица или нет. Конечно, может случиться, что некоторые столбцы не будут превращены в столбцы единичной матрицы, но это нам и не требуется. Пусть всего в столбцы единичной матрицы преобразовано r столбцов. Если остались строки ниже r -й, они нулевые, иначе преобразования можно продолжить. Предложение доказано.

Рассмотрим упрощенную матрицу A’ . В ней есть невырожденная подматрица порядка r , а невырожденных подматриц большего порядка, очевидно, нет. Следовательно, ранг матрицы равен r , а подматрица базисная.

Из этого следует, что \mathbf\,A=r , так как ранг не изменился при элементарных преобразованиях. За базисную подматрицу в A можно принять подматрицу, расположенную в столбцах с номерами j_<1>. j_ и строках, которые после перестановок попали на места 1. r в упрощенной матрице. Это видно из того, что, преобразуя матрицу, мы не прибавляли к пересекающим ее строкам никаких строк, которые ее не пересекают.

Таким образом, если мы не знали ранга матрицы и ее базисной подматрицы, то приведя ее к упрощенному виду, мы их определим. С другой стороны, имеет место

Какова бы ни была базисная подматрица матрицы A , элементарными преобразованиями строк можно привести A к такому упрощенному виду, в котором базисные столбцы будут первыми столбцами единичной матрицы.

Действительно, небазисные строки можно обратить в нулевые, вычитая из них подходящие линейные комбинации базисных. После этого можно превратить базисную подматрицу в единичную так, как это было сделано здесь. (Элементарные преобразования производятся, конечно, над полными строками.)