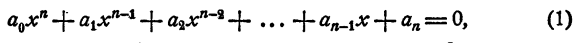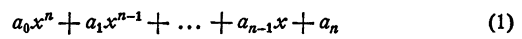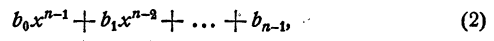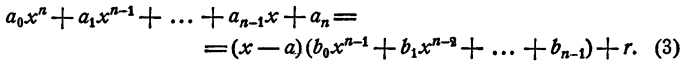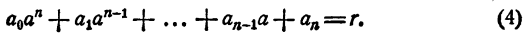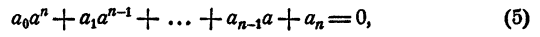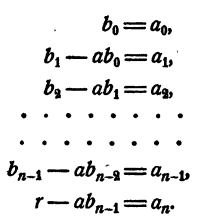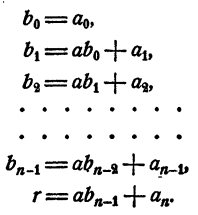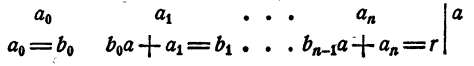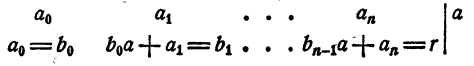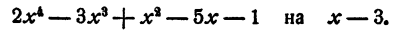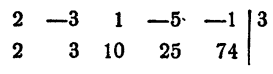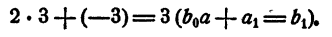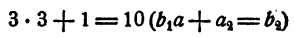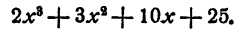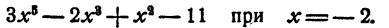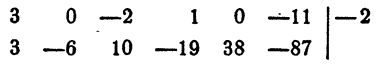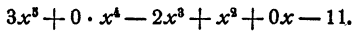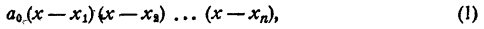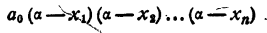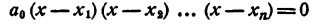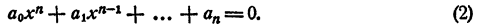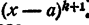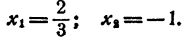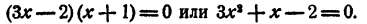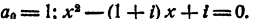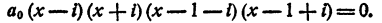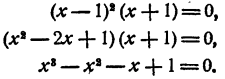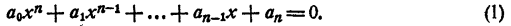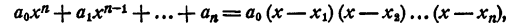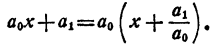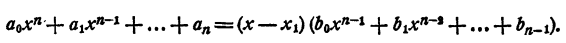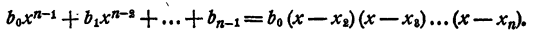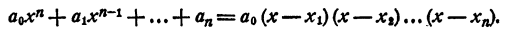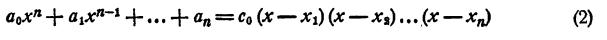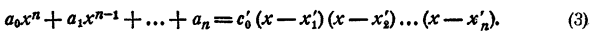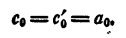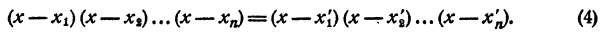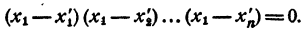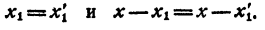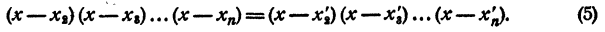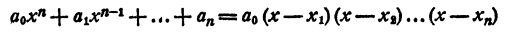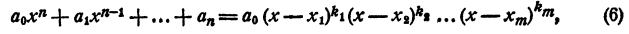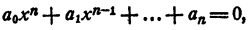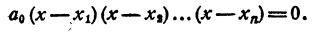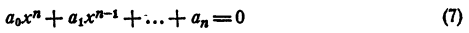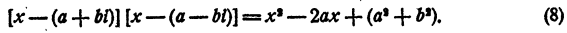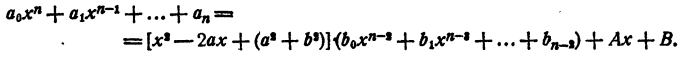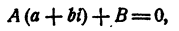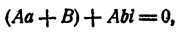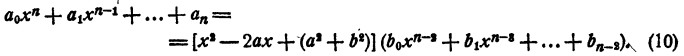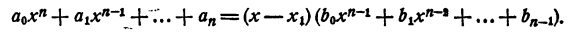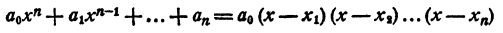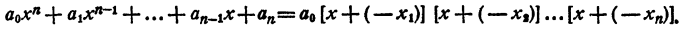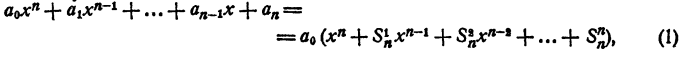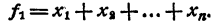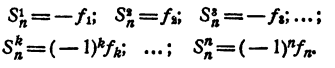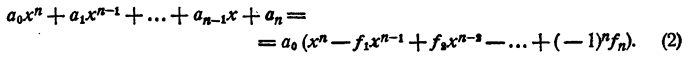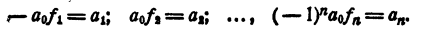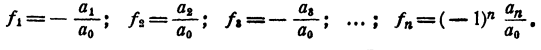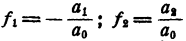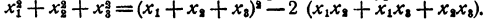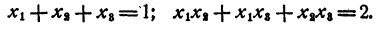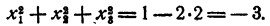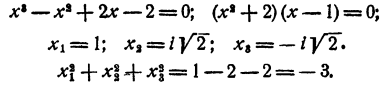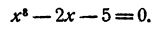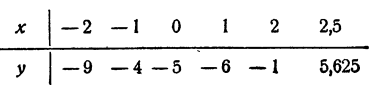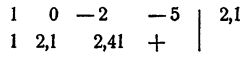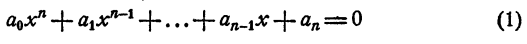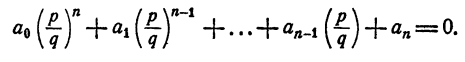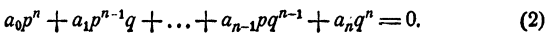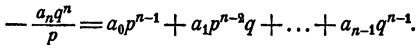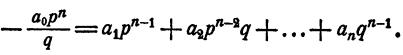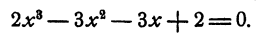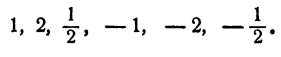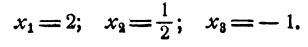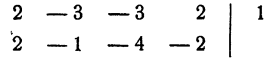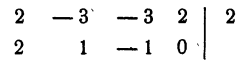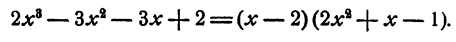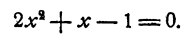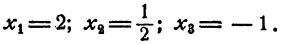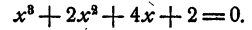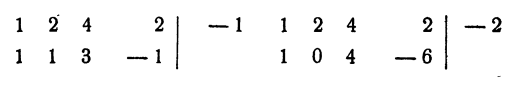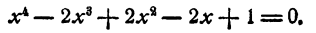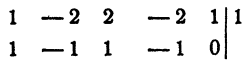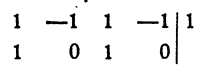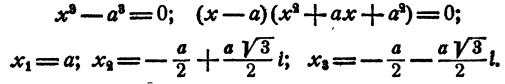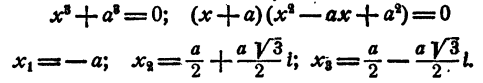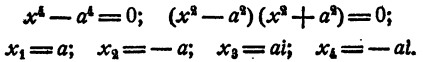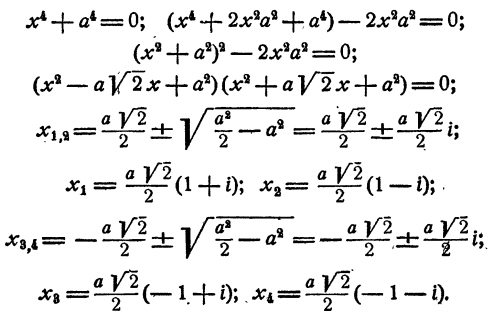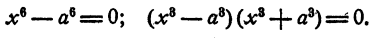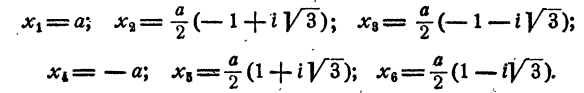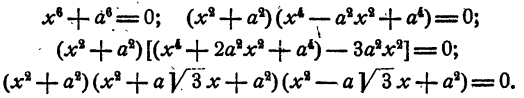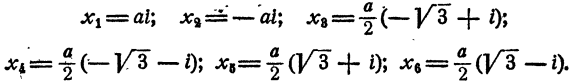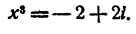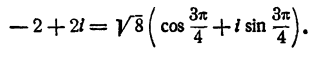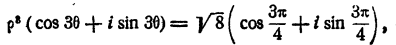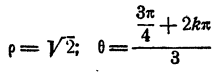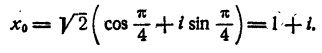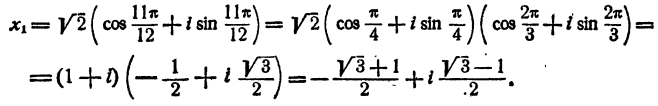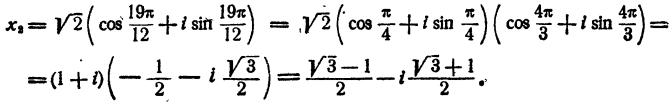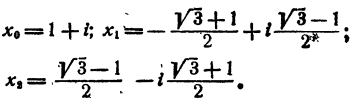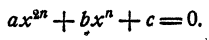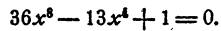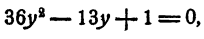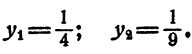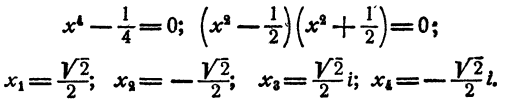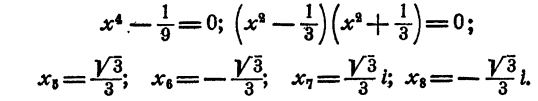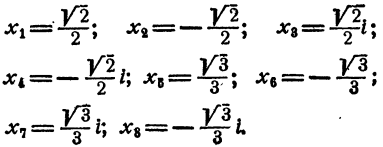Уравнения высших степеней в математике с примерами решения и образцами выполнения
Уравнение n-й степени с одним неизвестным:
Определение:
Уравнением n-й степени с одним неизвестным х называется уравнение
где 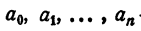
Изучение уравнения (1) в общем виде выходит за рамки школьного курса алгебры. В этой главе рассматриваются лишь некоторые свойства уравнения (1) и, кроме того, изучаются некоторые его частные виды.
Деление многочлена относительно х на х—а
Теорема:
Остаток от деления многочлена относительно х на двучлен х — а равен значению этого многочлена при х, равном а.
Доказательство:
Разделим многочлен n-й степени
на двучлен х — а. Как известно, частным (неполным) в этом случае будет многочлен n— 1 степени
а остатком — некоторое число r. Так как делимое равно делителю, умноженному на частное, плюс остаток, то
Равенство (3) есть тождество, оно справедливо при любых значениях х. В частности, оно справедливо и при х = а. При х = а. первое слагаемое правой части равенства (3) обращается в нуль, а потому
Следствие:
Для того чтобы многочлен относительно х делился на двучлен х — а, необходимо и достаточно, чтобы число а было корнем этого многочлена, т. е. чтобы при х = а многочлен обращался в нуль.
Доказательство:
Необходимость:
Пусть многочлен (1) делится на х — а, т. е. остаток r равен нулю. Тогда на основании равенства (4)
т. е. а — корень многочлена (1).
Достаточность:
Пусть а — корень многочлена (1), т. е. имеет место равенство (5). Тогда на основании равенства (4) r = 0, т. е. многочлен (1) делится на двучлен х — а.
Рассмотрим вновь тождество (3). Если в правой части его раскрыть скобки и сделать приведение подобных членов, в результате должен получиться тот же многочлен, что и в левой части. На этом основании, приравнивая коэффициенты при одинаковых степенях х, получаем
Перепишем эти равенства так:
Полученные равенства показывают, что коэффициенты частного и остаток, т. е. 
Пример:
Решение:
Первый коэффициент 2 второй строки просто сносится (b₀ = а₀). Второй коэффициент 3 получен так:
Третий коэффициент 10 получен так:
и т. д. Неполное частное равно
Пример:
Найти значение многочлена
Решение:
Искомое значение многочлена равно остатку от деления многочлена на x + 2
В двух местах первой строки потребовалось вписать 0. Объясняется это тем, что делимое имеет следующий вид:
Обычно члены, коэффициенты которых равны нулю, пропускаются. Здесь их пропускать нельзя.
Составление уравнения n-й степени по его корням
Теорема:
Каковы бы ни были числа 
где a₀ — любое число, отличное от нуля. При x = x₁ двучлен x — x₁ обращается в нуль, значит, при этом значении х обращается в нуль и произведение (1). При х = х₂ обращается в нуль двучлен х — x₂, и опять произведение (1) обращается в нуль. То же самое происходит при х =x₃; х = хₙ.
Пусть теперь х = а, где a — число, отличное от x₁ x₂ , …., хₙ . Ни одна из разностей а— x₁ а— x₂ ,…..о— хₙ „ не равна нулю. Число а₀ тоже отлично от нуля. Значит, и произведение
отлично от нуля.
Таким образом, уравнение
имеет корнями x₁ x₂ , …., хₙ и только эти числа.
Раскрыв скобки и выполнив приведение подобных членов, получим в левой части уравнения многочлен n-й степени относительно х, т. е.
Корнями уравнения (2) являются числа x₁ x₂ , …., хₙ и только эти числа.
Возможно, что корни x₁ x₂ , …., хₙ уравнения (2) не все различны между собой. В этих случаях говорят, что уравнение (2) имеет кратные корни. Так, например, если x₁ = x₂ и отлично от других корней уравнения (2), число является корнем второй кратности уравнения (2). Левая часть уравнения (2) делится в этом случае на (x — x₁ )³ и не делится на (х — x₁)³. Если x₁ = x₂ = x₃ и отлично от других корней уравнения (2), число x₁ является корнем третьей кратности уравнения (2). Левая часть уравнения (2) делится в этом случае на (х — x₁ )³ и не делится на (х— x₁ )⁴.
Вообще корнем кратности k уравнения (2) называется такое число а, что левая часть уравнения (2) делится на (х — а)ᵏ и не делится на
Пример:
Составить уравнение второй степени, корни которого
Решение:
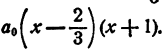
Пример:
Составить уравнение второй степени, корни которого x₁ = 1; х₂ =i.
Решение:
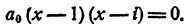
Пример:
Составить уравнение четвертой степени, корни которого i; —i; 1+i; 1-i
Решение:
Пример:
Составить уравнение третьей степени, корни которого x₁ = 1; х₂ = 1; х₃ = — 1.
Решение:
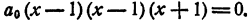
Число единица является здесь корнем второй кратности,
Основная теорема алгебры и некоторые следствия из нее
Мы видели, что, выбрав произвольные п комплексных чисел, можно составить уравнение п-й степени, корнями которого будут выбранные числа. Коэффициенты этого уравнения могут при -этом оказаться как вещественными, так и мнимыми. Возникает следующий весьма важный вопрос.
Дано уравнение n-й степени с комплексными коэффициентами
Можно ли утверждать, что среди комплексных чисел найдется хоть одно число, являющееся корнем этого уравнения?
В свое время мы видели, что среди целых чисел нет числа, являющегося корнем уравнения 2х— 3 = 0 с целыми коэффициентами. Среди положительных чисел нет числа, являющегося корнем уравнения x+ 1 = 0 с положительными коэффициентами.
Среди рациональных чисел нет числа, являющегося корнем уравнения x² — 2 = 0 с рациональными коэффициентами. Среди действительных чисел нет числа, являющегося корнем уравнения x²+ 1 = 0 с действительными коэффициентами.
Понятно поэтому, сколь важное значение имеет поставленный вопрос. Ответ на него дает основная теорема алгебры.
Всякое уравнение n-й степени с любыми комплексными коэффициентами имеет комплексный корень.
Доказательство этой теоремы выходит за рамки школьной программы.
Теорема:
Всякий многочлен n-й степени с любыми комплексными коэффициентами может быть представлен и притом единственным образом в виде произведения п двучленов первой степени, т. е.
где a ≠ 0, n ≥ 1. (Два таких разложения, отличающиеся только порядком расположения множителей, не считаются различными.)
Доказательство:
Доказательство разбивается на две части. В первой части доказывается возможность представления многочлена n-й степени в виде произведения п двучленов первой степени, во второй—единственность такого представления.
Для n = 1 теорема верна, так как
Предположим, что теорема справедлива для многочленов степени n—1.
Согласно основной теореме алгебры многочлен 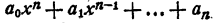
Для многочлена 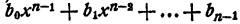
Допустим, что имеется два таких разложения:
Так как коэффициенты при хⁿ в правой и левой частях равенств (2) и (3) должны быть равны, то
Приравниваем правые части равенств (2) и (3). После сокращения на а₀ имеем
Методом математической индукции докажем, что правая и левая части равенства (4) состоят из соответственно равных множителей, но, быть может, записанных в другом порядке.
Для n= 1 утверждение, очевидно, справедливо.
Пусть утверждение справедливо для произведений, состоящих из n—1 множителей. Докажем, что утверждение справедливо и для произведений, состоящих из n множителей.
Левая часть равенства (4) при x = x₁ обращается в нуль. Значит, при x = x₁ обращается в нуль и правая часть этого равенства, т. е.
Произведение равно нулю. Значит, хоть один из сомножителей равен нулю. Допустим, что 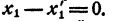
Сократим равенство (4) на х— x₁ получим
По допущению правая и левая части равенства (5) состоят из соответственно равных множителей, но, быть может, записанных в другом порядке. Приписав в каждую часть равенства (5) по одинаковому множителю х— x₁ получим, что правая и левая части равенства (4) состоят из соответственно равных сомножителей.
Теорема доказана полностью.
некоторые из сомножителей правой части могут быть одинаковы. Обозначив 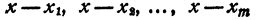
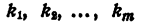
где 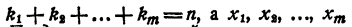
Представление левой части уравнения в виде (6) называется представлением левой части уравнения в канонической форме.
Теорема:
Всякое уравнение п-й степени с любыми комплексными коэффициентами имеет ровно п корней, среди которых могут быть и равные друг другу.
Доказательство:
где a₀ ≠ 0, n ≥ 0 Как доказано, левая часть может быть представлена в виде произведения n множителей первой степени. Таким образом, имеем
При x=x₁; х = х₂; х=хₙ левая часть уравнения превращается в нуль и, следовательно, х₁, х₂, …,xₙ— корни уравнения. Покажем, что никакое число а, отличное от х₁ х₂,…..хₙ, не может быть корнем этого уравнения.
Действительно, произведение а₀ (а — x₁) (а — х ₂ ,)… (а — x ₙ )не равно нулю, так как ни один из множителей его не равен нулю. Таким образом, корнями рассматриваемого уравнения являются числа x₁; х ₂ ;…; x ₙ и других корней нет.
Следствие:
Уравнение n-й степени имеет n корней, если каждый корень считать столько раз, какова его кратность.
Теорема:
Если уравнение n-й степени имеет действительные коэффициенты и мнимое число а + bi является корнем этого уравнения, то и сопряженное число а — bi является также корнем этого уравнения.
Доказательство:
Пусть мнимое число а + bi является корнем уравнения
с действительными коэффициентами. Требуется доказать, что сопряженное число а — bi также является корнем уравнения (7). Составим многочлен
Этот многочлен имеет действительные коэффициенты. Разделим левую часть уравнения (7) на многочлен (8). В частном получим многочлен n— 2 степени с действительными коэффициентами, в остатке многочлен степени не выше первой и тоже с действительными коэффициентами.
Так как делимое равно делителю, умноженному на частное плюс остаток, то
Положим в этом равенстве х = а + bi . Получим
так как и левая часть равенства и трехчлен 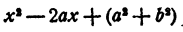
Так как b ≠ 0, то A = 0. Из первого уравнения системы (9) имеем В = 0. Выходит, что остаток Ах + В равен нулю, т. е.
При х = а — bi первый сомножитель правой части равенства (10) превращается в нуль, значит, и левая часть равенства тоже обращается в нуль. Значит, число а — bi является корнем уравнения (7).
Теорема:
Всякий многочлен n-й степени с действительными коэффициентами может быть представлен в виде произведения многочленов первой или второй степени с действительными коэффициентами.
Доказательство этой теоремы проводится методом математической индукции. Теорема, очевидно, справедлива для многочленов первой и второй степени. При этом многочлен второй степени либо имеет действительные корни и тогда разлагается на множители первой степени с действительными коэффициентами, либо он имеет два мнимых сопряженных корня, и тогда он на множители с действительными коэффициентами не разлагается.
Допустим, что теорема справедлива для многочленов n— 2 степени и многочленов n—1 степени. Докажем, что тогда она справедлива и для многочленов n-й степени.
Пусть 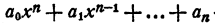
Если этот многочлен имеет действительный корень x₁ то он представляется в виде произведения многочлена первой степени на многочлен n—1 степени с действительными коэффициентами, т. е.
Если же многочлен действительных корней не имеет, то он имеет мнимый корень а + bi и сопряженный с ним корень а — bi. В этом случае многочлен представляется в виде произведения трехчлена второй степени на многочлен n— 2 степени с действительными коэффициентами, т. е.
Так как теорема для многочленов п—1 степени и многочленов n— 2 степени справедлива, то она справедлива и для многочленов степени n.
Теорема Виета
легко получить теорему Виета для уравнений любой степени. Перепишем это равенство так:
К правой части этого равенства применим правило умножения двучленов, первые члены которых одинаковы (см. гл. VIII, § 5). Получаем
где 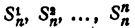
Знаком f₂ обозначим сумму всевозможных произведений корней, взятых по два. Подобный же смысл имеют знаки f₃, f₄, …, f ₙ . Тогда
Равенство (1) теперь можно переписать так:
Приравнивая коэффициенты при одинаковых степенях х в правой и левой частях равенства (2), получим
Последние равенства и выражают теорему Виета для уравнения любой степени. При n= 2, т. е. для уравнения 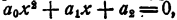
Пример:
Не решая уравнения 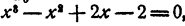
Решение:
Пусть х₁ x₂, х₃, — корни данного уравнения. Рассмотрим равенство
По теореме Виета
Полученный результат означает, что среди чисел х₁ x₂, х₃, имеются мнимые, иначе сумма квадратов их не могла бы быть отрицательной.
Предложенное уравнение нетрудно решить и подсчитать сумму квадратов корней непосредственно:
О решении уравнений высших степеней
Прежде всего возникает такой вопрос: можно ли для уравнений любой степени составить формулы для выражения корней уравнения через его коэффициенты, подобно известной формуле для квадратного уравнения? Оказывается, что это можно сделать для уравнений 3-й и 4-й степени, при этом формулы эти содержат столь сложные радикалы, что на практике ими предпочитают не пользоваться.
Что же касается уравнений выше 4-й степени, то доказано, что для них при помощи радикалов такие формулы составить нельзя.
В математике разработан ряд способов, дающих возможность вычислить любой корень любого уравнения с любой точностью. Один из таких способов разработан великим русским математиком, творцом неевклидовой геометрии Н. И. Лобачевским.
Ограничимся рассмотрением графического способа. Этот способ может применяться для вычисления действительных корней уравнений с действительными коэффициентами.
Пример:
Вычислить вещественные корни уравнения
Решение:
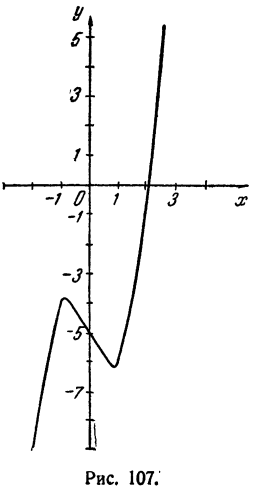
Построим график функции у = х³ — 2х— 5 (рис. 107). Имеем
Нетрудно видеть, что при x > 2,5 первое слагаемое х³ будет столь большим сравнительно с остальными, что у будет положительным числом.
По мере продвижения направо от х = 2,5 график будет подниматься кверху и, следовательно, больше пересекать ось Ох не будет.
Точно так же при х
Это означает, что точка 2,1 лежит правее корня, так как соответствующая ордината положительна (см. график).
Таким образом, 2 Вычисление рациональных корней уравнений с целыми коэффициентами
Теорема:
Для того чтобы несократимая дробь 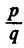
с целыми коэффициентами, необходимо, чтобы р было делителем свободного члена аₙ, a q было делителем старшего коэффициента а₀.
Доказательство:
Пусть 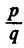
Умножим обе части тождества на qⁿ, получим
Из тождества (2) имеем
Правая часть равенства — целое число. Значит, 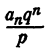
По условию, дробь 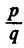
Из тождества (2) имеем
Так как ни одно простое число, входящее в q, не входит в р, число 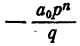
Следствие:
Если уравнение имеет целые коэффициенты и старший из них равен единице, то рациональными корнями такого уравнения могут быть только целые числа.
Действительно, а₀ = 1, a q — делитель а₀ . Значит, q = ± 1, а тогда 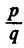
Следствие:
Целые корни уравнения с целыми коэффициент тами являются делителями свободного члена.
Пример:
Вычислить рациональные корни уравнения
Решение:
Свободный член равен 2. Поэтому для р возможны только следующие значения: 1, —1, 2 и —2.
Старший коэффициент равен 2. Поэтому для q возможны только следующие значения: 1, —1, 2, —2.
Составляя всевозможными способами несократимые дроби 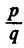
Подстановкой в уравнение легко выяснить, что из этих шести
чисел удовлетворяют уравнению 2, 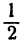
Таким образом, уравнение имеет три рациональных корня:
Для испытания, является ли данное число корнем уравнения, удобно пользоваться правилом сокращенного деления многочлена на двучлен х — а. Для данного примера эти испытания проводятся так:
1 не является корнем уравнения, так как при делении левой части уравнения на х — 1 в остатке получилось — 2.
Испытываем число 2
2 — корень уравнения. В результате деления оказалось, что
Поэтому для отыскания остальных корней данного уравнения достаточно решить уравнение
Ответ.
Пример:
Найти рациональные корни уравнения
Решение:
Старший коэффициент уравнения равен единице, поэтому рациональными корнями уравнения могут быть только целые числа.
Делители свободного члена суть: 1,2, — 1, — 2. Сразу видно,-что никакое положительное число не может быть корнем данного уравнения, так как при любом положительном значении х левая часть уравнения положительна. Остается испытать — 1 и — 2:
Ответ. Уравнение рациональных корней не имеет.
Полученный в последнем примере результат означает, что корни рассматриваемого уравнения иррациональные или мнимые.
Пример:
Решение:
Выясним прежде всего, не имеет ли уравнение рациональных корней. Испытанию подлежат два числа 1 и — 1:
x₁² = 1. Остальные корни данного уравнения являются корнями уравнения третьей степени х³ — х² + х —1=0:
x₂ = 1. Остальные корни данного уравнения являются корнями квадратного уравнения х² + 1 = 0.
Ответ. x₁ = x₂ = 1; х₃ = i; x₄= — 1.
Решение двучленных уравнений 3-й, 4-й и 6-й степени
Определение. Двучленным уравнением n-й степени называется уравнение вида 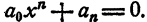
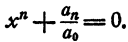
В этом параграфе излагается решение двучленных уравнений с действительными коэффициентами при n= 3, 4 и 6.
Уравнение имеет один действительный и два мнимых сопряженных корня.
Уравнение имеет один действительный и два мнимых сопряженных корня.
Уравнение имеет два действительных и два мнимых сопряженных корня.
Уравнение имеет две пары мнимых сопряженных корней.
Уравнение распадается на два кубических двучленных уравнения. На основании рассмотренного в п. а)
Уравнение имеет два действительных и две пары мнимых сопряженных корней
Уравнение распадается на три квадратных уравнения. Решая их, получаем
Уравнение имеет три пары мнимых сопряженных корней.
Замечание. Пользуясь извлечением корня n-й степени из комплексного числа, можно решить двучленное уравнение хⁿ = а любой степени n при любой правой части а.
Корнями уравнения хⁿ = а являются все значения корня n-й степени из а.
Пример:
Решение:
Запишем правую часть уравнения в тригонометрической форме
Пусть кубический корень из —2 + 2i равен р (cos 0 +isin 0). Тогда имеем
отсюда (§ 9 гл. IX) имеем
Для получения всех значений корня достаточно k положить равным 0, 1, 2. При k = 0 имеем
Решение трехчленных уравнений
Определение:
Трехчленным уравнением называется уравнение вида
При n= 2 уравнение является биквадратным.
Решение трехчленного уравнения подстановкой хⁿ = у сводятся к квадратному уравнению ay² + by + с = 0 и двучленному уравнению n-й степени.
Пример:
Решение:
Положим x⁴ = у. Имеем
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Корень n-ой степени
Определение корня n-й степени из действительного числа
Корнем n-й степени (\(n=2, 3, 4, 5, 6… \)) некоторого числа \(a\) называют такое неотрицательное число \(b\), которое при возведении в степень \(n\) дает \(a\):
Число \(n\) при этом называют показателем корня.
Если \(n=2\), то перед вами корень 2-й степени или обычный квадратный корень.
Если \(n=3\), то корень 3-й степени и т.д.
Операция извлечения корня n-й степени является обратной к операции возведения в n-ю степень.
Кубический корень из числа 27 равняется 3. Действительно, если число 3 возвести в 3-ю степень, то мы получим 27.
Корень 4-й степени из 16-и равен 2. Двойка в 4-й степени равна 16.
Если извлечь корень n-й степени из 0, всегда будет 0.
Мы не можем в уме подобрать такое число, которое при возведении в 3-ю степень даст 19. Если посчитать на калькуляторе, то получим \(2,668…\) – иррациональное число с бесконечным количеством знаков после запятой.
Обычно, в математике, когда у вас получается иррациональное число, корень не считают и оставляют так как есть \(\sqrt[3]<19>\).
Что же делать, если под рукой нет калькулятора, а нужно оценить, чему равен такой корень. В этом случае нужно подобрать справа и слева такие ближайшие числа, корень из которых посчитать можно:
$$ \sqrt[3] <8>\le \sqrt[3] <19>\le \sqrt[3] <27>$$ $$ 2 \le \sqrt[3] <19>\le 3 $$
Получается, что наш корень лежит между числами 2 и 3.
Корень четной и нечетной степени
Надо четко различать правила работы четными и нечетными степенями. Дело в том, что корень четной степени можно взять только из положительного числа. Из отрицательных чисел корень четной степени не существует.
Корень нечетной степени можно посчитать из любых действительных чисел. Иногда в школьной программе встречаются задания, в которых требуется определить имеет ли смысл выражение:
Данное выражение имеет смысл, так как корень нечетной степени можно посчитать из любого числа, даже отрицательного.
Так как корень четной степени, а под корнем стоит отрицательное число, то выражение не имеет смысла.
Свойства корня n-й степени
Пусть есть два неотрицательных числа a и b, для них будут выполняться следующие свойства:
Корни нужны для точных и сокращенных подсчетов в математике. Это необходимая функция, без которой представить современную математику невозможно. Корень n-ой степени обозначается при помощи всем известного значка радикала. Даже самый простой корень из двух будет равен длинному набору чисел, округлив который вы получите лишь приблизительное значение. Такие числа называются иррациональными и намного лучше представить их в виде радикала.
Основные ограничения и свойства
- Корень четной степени существует только из положительных чисел. Число, возводимое в четную степень, а затем извлеченное из той же степени не становится исходным, а превращается в модуль этого числа.
- Из-под знака нечетного показателя корня можно выносить минус. Это упрощает процесс подсчета.
В данном учебном ролике в понятной форме изложены все основные свойства и теоремы корней n-ой степени. Тема непонятна для большинства школьников 7-9 классов, но не по причине их сложности (всего пара определений и свойств), а вследствие неправильной подачи информации в учебниках. Поэтому в данном видео мы расскажем о самом грамотном и понятном определении корня – все то, что действительно нужно запомнить. Далее покажем, как все это можно применить на практике.
Корни бывают четные и нечетные. Основные определения, необходимые для изучения данной темы звучат так: корень четной степени n из числа a — это любое неотрицательное число b, которое при умножении на само себя n раз даст число a . А корень нечетной степени n из числа a — это любое неотрицательное или отрицательное число b, которое также при умножении на само себя даст a.
Лекция по теме «Уравнения высших степеней. Методы их решения». 9-й класс
Разделы: Математика
Класс: 9
- Закрепить понятие целого рационального уравнения -й степени.
- Сформулировать основные методы решения уравнений высших степеней (n > 3).
- Обучить основным методам решения уравнений высших степеней.
- Научить по виду уравнения определять наиболее эффективный способ его решения.
Формы, методы и педагогические приемы, которые используются учителем на уроке:
- Лекционно-семинарская система обучения (лекции – объяснение нового материала, семинары – решение задач).
- Информационно-коммуникационные технологии (фронтальный опрос, устная работа с классом).
- Дифференцированное обучение, групповые и индивидуальные формы.
- Использование исследовательского метода в обучении, направленного на развитие математического аппарата и мыслительных способностей каждого конкретного ученика.
- Печатный материал – индивидуальный краткий конспект урока (основные понятия, формулы, утверждения, материал лекций сжато в виде схем или таблиц).
- Организационный момент.
Цель этапа: включить учащихся в учебную деятельность, определить содержательные рамки урока. - Актуализация знаний учащихся.
Цель этапа: актуализировать знания учащихся по изученным ранее смежным темам - Изучение новой темы (лекция). Цель этапа: сформулировать основные методы решения уравнений высших степеней (n > 3)
- Подведение итогов.
Цель этапа: еще раз выделить ключевые моменты в материале, изученном на уроке. - Домашнее задание.
Цель этапа: сформулировать домашнее задание для учащихся.
1. Организационный момент.
Формулировка темы урока: “Уравнения высших степеней. Методы их решения”.
2. Актуализация знаний учащихся.
Теоретический опрос – беседа. Повторение некоторых ранее изученных сведений из теории. Учащиеся формулируют основные определения и дают формулировки необходимых теорем. Приводят примеры, демонстрируя уровень полученных ранее знаний.
- Понятие уравнения с одной переменной.
- Понятие корня уравнения, решения уравнения.
- Понятие линейного уравнения с одной переменной, понятие квадратного уравнения с одной переменной.
- Понятие равносильности уравнений, уравнения-следствия (понятие посторонних корней), переход не по следствию (случай потери корней).
- Понятие целого рационального выражения с одной переменной.
- Понятие целого рационального уравнения n-й степени. Стандартный вид целого рационального уравнения. Приведенное целое рациональное уравнение.
- Переход к совокупности уравнений более низких степеней путем разложения исходного уравнения на множители.
- Понятие многочлена n-й степени от x. Теорема Безу. Следствия из теоремы Безу. Теоремы о корнях (Z-корни и Q-корни) целого рационального уравнения с целыми коэффициентами (соответственно приведенного и неприведенного).
- Схема Горнера.
3. Изучение новой темы.
Будем рассматривать целое рациональное уравнение n-й степени стандартного вида с одной неизвестной переменной x : Pn(x) = 0 , где Pn(x) = anx n + an-1x n-1 + a1x + a0 – многочлен n-й степени от x, an ≠ 0 . Если an = 1 то такое уравнение называют приведенным целым рациональным уравнением n-й степени. Рассмотрим такие уравнения при различных значениях n и перечислим основные методы их решения.
n = 1 – линейное уравнение.
n = 2 – квадратное уравнение. Формула дискриминанта. Формула для вычисления корней. Теорема Виета. Выделение полного квадрата.
n = 3 – кубическое уравнение.
Пример: x 3 – 4x 2 – x + 4 = 0 

Возвратное кубическое уравнение вида ax 3 + bx 2 + bx + a = 0. Решаем, объединяя члены с одинаковыми коэффициентами.
Пример: x 3 – 5x 2 – 5x + 1 = 0 



Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы. Схема Горнера. При применении этого метода необходимо сделать акцент на том, что перебор в данном случае конечный, и корни мы подбираем по определенному алгоритму в соответствии с теоремой о Z-корнях приведенного целого рационального уравнения с целыми коэффициентами.
Пример: x 3 – 9x 2 + 23x – 15 = 0. Уравнение приведенное. Выпишем делители свободного члена <+1; +3; +5; +15>. Применим схему Горнера:
| x 3 | x 2 | x 1 | x 0 | вывод | |
| 1 | -9 | 23 | -15 | ||
| 1 | 1 | 1 х 1 – 9 = -8 | 1 х (-8) + 23 = 15 | 1 х 15 – 15 = 0 | 1 – корень |
| x 2 | x 1 | x 0 |
Получаем 

Уравнение с целыми коэффициентами. Подбор Q-корней на основании теоремы. Схема Горнера. При применении этого метода необходимо сделать акцент на том, что перебор в данном случае конечный и корни мы подбираем по определенному алгоритму в соответствии с теоремой о Q-корнях неприведенного целого рационального уравнения с целыми коэффициентами.
Пример: 9x 3 + 27x 2 – x – 3 = 0. Уравнение неприведенное. Выпишем делители свободного члена <+1; +3>. Выпишем делители коэффициента при старшей степени неизвестного. <+1; +3; +9> Следовательно, корни будем искать среди значений <+1; +

| x 3 | x 2 | x 1 | x 0 | вывод | |
| 9 | 27 | -1 | -3 | ||
| 1 | 9 | 1 x 9 + 27 = 36 | 1 x 36 – 1 = 35 | 1 x 35 – 3 = 32 ≠ 0 | 1 – не корень |
| -1 | 9 | -1 x 9 + 27 = 18 | -1 x 18 – 1 = -19 | -1 x (-19) – 3 = 16 ≠ 0 | -1 – не корень |
 | 9 |  x 9 + 27 = 30 x 9 + 27 = 30 |  x 30 – 1 = 9 x 30 – 1 = 9 |  x 9 – 3 = 0 x 9 – 3 = 0 | корень |
| x 2 | x 1 | x 0 |
Получаем 




Для удобства подсчета при подборе Q-корней бывает удобно сделать замену переменной, перейти к приведенному уравнению и подбирать Z-корни.
- Если можно воспользоваться заменой вида y = kx.
Формула Кардано. Существует универсальный метод решения кубических уравнений – это формула Кардано. Эту формулу связывают с именами итальянских математиков Джероламо Кардано (1501–1576), Николо Тарталья (1500–1557), Сципиона дель Ферро (1465–1526). Эта формула лежит за рамками нашего курса.
n = 4 – уравнение четвертой степени.
Пример: x 4 + 2x 3 + 5x 2 + 4x – 12 = 0 



Метод замены переменной.
- Возвратное уравнение четвертой степени вида ax 4 + bx 3 + cx 2 + bx + a = 0.
Решаем, объединяя члены с одинаковыми коэффициентами, путем замены вида
- Обобщенное возвратное уравнение четвертой степени вида ax 4 + bx 3 + cx 2 – bx + a = 0.
- Обобщенное возвратное уравнение четвертой степени вида ax 4 + bx 3 + cx 2 + kbx + k 2 a = 0.
- Замена общего вида. Некоторые стандартные замены.
Пример 3. Замена общего вида (вытекает из вида конкретного уравнения).
Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Уравнение с целыми коэффициентами. Подбор Q-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Формула общего вида. Существует универсальный метод решения уравнений четвертой степени. Эту формулу связывают с именем Людовико Феррари (1522–1565). Эта формула лежит за рамками нашего курса.
n > 5 – уравнения пятой и более высоких степеней.
Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Уравнение с целыми коэффициентами. Подбор Q-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Симметрические уравнения. Любое возвратное уравнение нечетной степени имеет корень x = -1 и после разложения его на множители получаем, что один сомножитель имеет вид (x + 1), а второй сомножитель – возвратное уравнение четной степени (его степень на единицу меньше, чем степень исходного уравнения). Любое возвратное уравнение четной степени вместе с корнем вида x = φ содержит и корень вида 
Метод замены переменной. Использование однородности.
Не существует формулы общего вида для решения целых уравнений пятой степени (это показали итальянский математик Паоло Руффини (1765–1822) и норвежский математик Нильс Хенрик Абель (1802–1829)) и более высоких степеней (это показал французский математик Эварист Галуа (1811–1832)).
- Напомним еще раз, что на практике возможно использование комбинации перечисленных выше методов. Удобно переходить к совокупности уравнений более низких степеней путем разложения исходного уравнения на множители.
- За рамками нашего сегодняшнего обсуждения остались широко используемые на практике графические методы решения уравнений и методы приближенного решения уравнений высших степеней.
- Бывают ситуации, когда у уравнения нет R-корней. Тогда решение сводится к тому, чтобы показать, что уравнение корней не имеет. Для доказательства анализируем поведение рассматриваемых функций на промежутках монотонности. Пример: уравнение x 8 – x 3 + 1 = 0 не имеет корней.
- Использование свойства монотонности функций. Бывают ситуации, когда использование различных свойств функций позволяет упростить поставленную задачу.
Пример 1: уравнение x 5 + 3x – 4 = 0 имеет один корень x = 1. По свойству монотонности анализируемых функций других корней нет.
Пример 2: уравнение x 4 + (x – 1) 4 = 97 имеет корни x1 = -2 и x2 = 3. Проанализировав поведение соответствующих функций на промежутках монотонности, заключаем, что других корней нет.
4. Подведение итогов.
Резюме: Теперь мы овладели основными методами решения различных уравнений высших степеней (для n > 3). Наша задача научиться эффективно использовать перечисленные выше алгоритмы. В зависимости от вида уравнения мы должны будем научиться определять, какой способ решения в данном случае является наиболее эффективным, а также правильно применять выбранный метод.
5. Домашнее задание.
[1]: п.7, стр. 164–174, №№ 33–36, 39–44, 46,47.
[4]: №№ 9.1–9.4, 9.6–9.8, 9.12, 9.14–9.16, 9.24–9.27.
Возможные темы докладов или рефератов по данной тематике:
- Формула Кардано
- Графический метод решения уравнений. Примеры решения.
- Методы приближенного решения уравнений.
Анализ усвоения материала и интереса учащихся к теме:
Опыт показывает, что интерес учащихся в первую очередь вызывает возможность подбора Z-корней и Q-корней уравнений при помощи достаточно простого алгоритма с использованием схемы Горнера. Также учащиеся интересуются различными стандартными типами замены переменных, которые позволяют существенно упрощать вид задачи. Особый интерес обычно вызывают графические методы решения. В этом случае дополнительно можно разобрать задачи на графический метод решения уравнений; обсудить общий вид графика для многочлена 3, 4, 5 степени; проанализировать, как связано число корней уравнений 3, 4, 5 степени с видом соответствующего графика. Ниже приведен список книг, в которых можно найти дополнительную информацию по данной тематике.
- Виленкин Н.Я. и др. “Алгебра. Учебник для учащихся 9 классов с углубленным изучением математики” – М., Просвещение, 2007 – 367 с.
- Виленкин Н.Я., Шибасов Л.П., Шибасова З.Ф. “За страницами учебника математики. Арифметика. Алгебра. 10-11 класс” – М., Просвещение, 2008 – 192 с.
- Выгодский М.Я. “Справочник по математике” – М., АСТ, 2010 – 1055 с.
- Галицкий М.Л. “Сборник задач по алгебре. Учебное пособие для 8-9 классов с углубленным изучением математики” – М., Просвещение, 2008 – 301 с.
- Звавич Л.И. и др. “Алгебра и начала анализа. 8–11 кл. Пособие для школ и классов с углубленным изучением математики” – М., Дрофа, 1999 – 352 с.
- Звавич Л.И., Аверьянов Д.И., Пигарев Б.П., Трушанина Т.Н. “Задания по математике для подготовки к письменному экзамену в 9 классе” – М., Просвещение, 2007 – 112 с.
- Иванов А.А., Иванов А.П. “Тематические тесты для систематизации знаний по математике” ч.1 – М., Физматкнига, 2006 – 176 с.
- Иванов А.А., Иванов А.П. “Тематические тесты для систематизации знаний по математике” ч.2 – М., Физматкнига, 2006 – 176 с.
- Иванов А.П. “Тесты и контрольные работы по математике. Учебное пособие”. – М., Физматкнига, 2008 – 304 с.
- Лейбсон К.Л. “Сборник практических заданий по математике. Часть 2–9 класс” – М., МЦНМО, 2009 – 184 с.
- Макарычев Ю.Н., Миндюк Н.Г. “Алгебра. Дополнительные главы к школьному учебнику 9 класса. Учебное пособие для учащихся школ и классов с углубленным изучением математики.” – М., Просвещение, 2006 – 224 с.
- Мордкович А.Г. “Алгебра. Углубленное изучение. 8 класс. Учебник” – М., Мнемозина, 2006 – 296 с.
- Савин А.П. “Энциклопедический словарь юного математика” – М., Педагогика, 1985 – 352 с.
- Сурвилло Г.С., Симонов А.С. “Дидактические материалы по алгебре для 9 класса с углубленным изучением математики” – М., Просвещение, 2006 – 95 с.
- Чулков П.В. “Уравнения и неравенства в школьном курсе математик. Лекции 1–4” – М., Первое сентября, 2006 – 88 с.
- Чулков П.В. “Уравнения и неравенства в школьном курсе математик. Лекции 5–8” – М., Первое сентября, 2009 – 84 с.
http://sigma-center.ru/root_of_degree_n
http://urok.1sept.ru/articles/646258