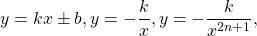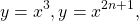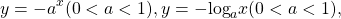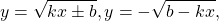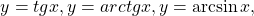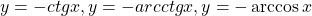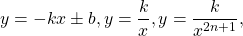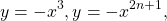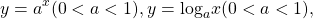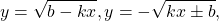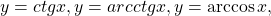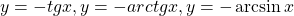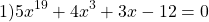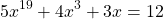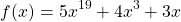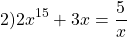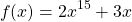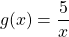Свойства возрастающей функции в уравнениях

Использование свойства монотонности функции при решении уравнений

Разделы: Математика

Цели:

Задачи:

Оборудование: карточки с заданиями для каждого ученика.

Организационный момент: сообщить тему урока, сформулировать цели урока.

Проводится фронтальный опрос учащихся:

1. Какие функции называются возрастающими (убывающими)?
2. Какие функции называются монотонными?
3. Какие свойства монотонных функций вы знаете?

Свойство 1. Если y=g(x) – монотонно возрастает на промежутке I и y=f(x) – монотонно возрастает на промежутке I, то y=g(x)+f(x) – монотонно возрастает на промежутке I.

Свойство 2. Если y=f(x) возрастает (убывает) на промежутке I, то уравнение f(x)=a имеет на I не более одного корня.

Свойство 3. Если y=f(x) возрастает на I, а y=g(x) убывает на I, то уравнение f(x)=g(x), имеет не более одного корня.

II. Решение уравнений

( Этот этап урока проходит в форме беседы учителя с учениками. Ученики, основываясь на прошлом опыте решения уравнений, предлагают свои решения. Учитель показывает им более рациональные способы решения этих уравнений)

Пример 1. Решите уравнение: x 5 +x 3 +2x-4=0.

Решение: Функция f(x)=x 5 +x 3 +2x-4 возрастает как сумма трех возрастающих функций y=x 5 , y=x 3 и y=2x-4 на R.

Тогда уравнение f(x)=0 имеет не более одного корня. Испытывая делители свободного члена, находим, что x=1.

Пример 2. Решите уравнение .

Решение: Функция — возрастает на своей области определения, как сумма двух возрастающих функций и . Следовательно, уравнение f(x)=2 имеет не больше одного корня на [-1,45; 26]. Непосредственно проверкой убеждаемся что f(1)=0. Уравнение решено: мы нашли корень и доказали, что других корней нет.

Учащимся предлагается решить это уравнение дома с помощью возведения в квадрат лавой и правой частей уравнения, и убедится что решение будет очень громоздким.

Пример 3. Решите уравнение log₂(x+2)=1-x.

Решение: Функция y=log₂(x+2) – возрастает на (-2; +). Функция y=1-x убывает на R. Тогда уравнение log₂(x+2)=1-x имеет единственное решение при x (-2; +).

Непосредственно проверкой убедимся, что x=0 является корнем этого уравнения.

Каким еще способом можно решить это уравнение? (графически)

Пример 4. Определите число корней уравнения .

Решение: Рассмотрим функцию эта функция возрастает на области определения , тогда , т.е. f(x)4, где x D(f). Значит множеством значений функции f(x) является промежуток [+4;+).

Т.е. при a4 уравнение имеет единственное решение, при a 5 +3x=4.

Решить уравнение .

II. Вариант:

Решить уравнение x 5 +7x=-8.

Решить уравнение .

1. Решить уравнение .

IV. К доске приглашаются ученики из обоих вариантов и показывают решение уравнений

V. Подведение итогов урока и выставление оценок

VI. Задание на дом

1. Определить число корней уравнения .
2. Решить уравнение x 5 +2x 3 +3=54.

[1] В.В. Локоть. Применение свойств функций, преобразование неравенств // АРКТИ, Москва 2007 г.

[2] Ю.Н. Макарычев. Дополнительные главы к школьному учебнику 9 класс // Просвещение, 1998 г.

[3] И.Я. Виленкин. Алгебра и математический анализ 10 // Просвещение, 1998 г.

[4] Е.Д. Кулакин. 3000 конкурсных задач по математике // Москва 2002 г.

Решение уравнений с помощью монотонности функций

Решение уравнений с помощью монотонности функций позволяет быстро и просто найти корень уравнения (либо доказать, что уравнение корней не имеет).

Использование возрастания и убывания функций при решении уравнений опирается на следующие теоремы.

1) Если на некотором промежутке функция f(x) возрастает (или убывает), то уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — постоянная величина (число)).

2) Если на некотором промежутке функция f(x) возрастает, а функция g(x) убывает (либо наоборот), то уравнение f(x)=g(x) на этом промежутке имеет единственный корень либо не имеет корней.

Доказав, что уравнение имеет на промежутке не более чем один корень, можно попытаться определить его подбором.

Если функция имеет несколько промежутков возрастания и убывания, каждый из них следует рассмотреть отдельно.

Сумма возрастающих функций — возрастающая функция. Сумма убывающих функций — убывающая функция.

Прибавление или вычитание постоянной величины не влияет на монотонность функции. Если к возрастающей функции прибавить (или вычесть) постоянную величину, получим возрастающую функцию. Если к убывающей функции прибавить (или вычесть) постоянную величину, получим убывающую функцию.

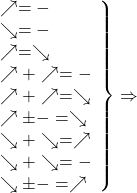
Таким образом, использование монотонности функций при решении уравнений схематически можно изобразить так:

то уравнение имеет единственный корень или не имеет корней.

Разумеется, количество слагаемых может быть больше двух.

Некоторые функции, возрастающие на всей области определения либо на каждом из промежутков, из объединения которых состоит область определения (k>0, b≥0, n — целое):

1),y = <\log _a>x(a > 1),\]» title=»Rendered by QuickLaTeX.com»/>

Некоторые функции, убывающие на всей области определения либо на каждом из промежутков, из объединения которых состоит область определения:

1),y = — <\log _a>x(a > 1),\]» title=»Rendered by QuickLaTeX.com»/>

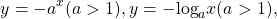
Примеры решения уравнений с помощью использования монотонности функций.

Перепишем уравнение в виде

является возрастающей (как сумма возрастающих функций). Следовательно, уравнение имеет не более одного корня. Подбором находим, что x=1.

На промежутке (-∞;0) функция

— убывает, следовательно, уравнение имеет не более одного корня. Подбором находим x= -1.

Аналогично, на промежутке (0:∞)

— убывает, следовательно, уравнение имеет не более одного корня. Подбором находим x=1.

В алгебре решение уравнений с применением возрастания и убывания функций чаше всего используется при решении иррациональных, логарифмических, показательных уравнений. Полезно взять на вооружение этот удобный и быстрый способ.

2 комментария

Добрый день. Вот это схематическое изображение монотонности очень интересно, но там не все понятно. Что вы подразумеваете под знаками равно и минус? И вот это: сумма убывающих_возрастающая? Буду благодарна комментариям

Елена, «=» — знак равенства между левой и правой частями уравнения.
Сумма убывающих функций — убывающая функция. Соответственно, одна часть уравнения — убывающая функция, а другая — возрастающая, то применима вторая теорема.
Аналогично, сумма возрастающих функций есть возрастающая функция. Если с одной стороны — возрастающая функция, с другой — убывающая, можем применить первую теорему.
Если к монотонно возрастающей функции прибавить число (или вычесть), то это никак не повлияет на её монотонность (это наглядно можно продемонстрировать графически: график функции y=f(x)±b получен из графика y=f(x) параллельным переносом на b единиц вверх или вниз вдоль оси Oy). Поэтому, если в одной части уравнения — монотонно возрастающая функция ± число, а в другой — монотонно убывающая функция, можем применить теорему два. И т.д.

Возрастание и убывание функции

Общие понятия о поведении функций

Исследуя функции, заданные определенными уравнениями, особенно уделяют внимание их свойствам, а именно возрастанию или убыванию.

Монотонной функцией называется функция, меняющаяся в одном направлении.
На графиках представлены примеры монотонно возрастающей и монотонно убывающей функций.

Соответственно, монотонная функция может быть возрастающая или убывающая.

Возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается, иными словами, чем больше значение аргумента, тем больше значение функции.

Математическое выражение этого определения выглядит следующим образом:

Убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается, иными словами, чем больше значение аргумента, тем меньшее значение функции.

Математическое выражение этого определения выглядит следующим образом:

Разберем примеры решения задач на изучение характера поведения функции.

Задача 1. Задана функция \(y=x^3+1\) . Исследовать ее характер в интервале \([0;2]\) .
Решение: Подставим поочередно крайние значения заданного отрезка и сравним полученные значения функции.
\(y_1=0^3+1=1\) ;
\(y_2=2^3+1=9\) .

Поскольку значения функции увеличиваются, при увеличении значений аргумента, то данная функция на заданном отрезке будет возрастать.

Задача 2 . Задана функция \(y=<1\over x>\) . Определить ее характер в интервале \([1;2]\) .
Решение: Подставим поочередно крайние значения заданного отрезка и сравним полученные значения функции.
\(y_1=<1\over 1>=1\) ;
\(y_2=<1\over2>=0.5\) .

Поскольку значения функции уменьшаются, при увеличении значений аргумента, то данная функция на данном отрезке будет убывать.

Не возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается или остается на том же уровне, иными словами, большему значению аргумента соответствует большее или равное значение функции.

Не нашли что искали?

Просто напиши и мы поможем

Не убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается или остается на том же уровне, иными словами, большему значению аргумента соответствует меньшее или равное значение функции.

Постоянной называется такая функция, которая не убывает и не возрастает, то есть при увеличении или при уменьшении значения аргумента, значение функции остается на одном и том же уровне. Пример такой функции можно наблюдать на рисунке.

Разберем задачу на исследование характера поведения функции. При данной функции \(y=5\) исследовать ее характер в интервале \([0;2]\) .

По сути эту функцию можно записать как \(y=5+0∙x\) , подставляя крайние значения отрезка, получим:
\(y_1=5+0∙0=5\) ;
\(y_2=5+0∙2=5\) .

То есть функция \(y=5\) будет постоянной.

Постоянная, не убывающая и не возрастающая функции не есть монотонные.

Свойства монотонных функций

К свойствам монотонных функций относятся такие характеристики:

• если две или больше возрастающих функций суммируются, то в результате получается тоже возрастающая функция;
• результатом произведения положительных возрастающих функций будет возрастающая функция;
• при композиции двух возрастающих функций получается также функция, которая будет возрастать;
• при положительной функции \(f(x)\) , функция \(f^n (x)\) тоже будет возрастать, при условии, что \(n\) является натуральным числом;
• при сохранении возрастающей функцией \(f(x)\) своего знака, обратная ей функция будет убывать;
• при возрастающей функции \(f(x)\) и константе c справедливо, что функции \(cf(x)\) и \(f(x)+c\) , при \(c>0\) , будут возрастать.

Монотонность производной и заданной функций связаны между собой, и это описано в таких теоремах: