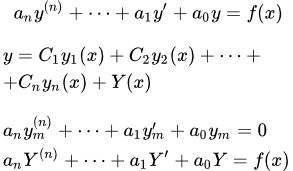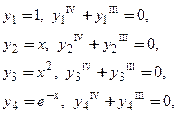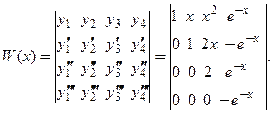Линейные дифференциальные уравнения с постоянными коэффициентами
Определения
Линейное дифференциальное уравнение с постоянными коэффициентами – это уравнение, линейное относительно зависимой переменной y и ее производных:
(1) .
Член f ( x ) называется неоднородной частью уравнения.
Линейное однородное дифференциальное уравнение с постоянными коэффициентами – это уравнение вида (1), неоднородная часть которого равна нулю:
.
Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами – это уравнение вида (1) с отличной от нуля неоднородной частью:
.
Здесь все коэффициенты a i – постоянные. n – порядок уравнения.
Свойства решений линейных дифференциальных уравнений с постоянными коэффициентами
Однородные уравнения
Рассмотрим линейное однородное дифференциальное уравнение:
(2) .
Общее решение такого уравнения можно записать в виде:
,
где – линейно независимые частные решения уравнения (2). Каждое из них удовлетворят уравнению (2):
.
В этом случае говорят, что функции образуют фундаментальную систему решений линейного однородного уравнения (2).
Фундаментальная система решений линейного однородного уравнения (2) – это n линейно независимых функций , каждая из которых является решением этого уравнения.
Линейно независимые функции – это такие функции, для которых соотношение
может выполняться только если все постоянные равны нулю.
Линейно зависимые функции – это функции, между которыми имеет место линейная зависимость:
,
где – постоянные, из которых хотя бы одна отлична от нуля.
Неоднородные уравнения
Рассмотрим линейное неоднородное дифференциальное уравнение:
(3) .
Пусть Y – частное решение этого уравнения. Тогда общее решение уравнения (3) равно сумме общего решения однородного уравнения плюс частное решение неоднородного:
.
Здесь – общее решение однородного уравнения:
;
Y – частное (любое) решение неоднородного уравнения:
.
Часто встречается случай, когда неоднородная часть может быть представлена в виде суммы функций:
.
Тогда частное решение Y также может быть представлено в виде суммы частных решений:
,
каждое из которых удовлетворяет уравнению с правой частью в виде одной из функций :
.
В некоторых случаях бывает легче решать отдельные частные решения от более простых неоднородных частей, а затем получать частное решение для всего уравнения, суммированием полученных частных решений.
Автор: Олег Одинцов . Опубликовано: 20-07-2013 Изменено: 13-12-2019
ЛИНЕЙНЫЕ ОДНОРОДНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
ЛИНЕЙНЫЕ ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
N-ГО ПОРЯДКА
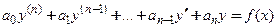
называется линейным неоднородным дифференциальным уравнением n-го порядка, если коэффициенты 
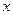
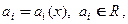
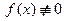
Если функция 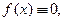
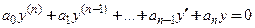
Уравнение (2) называют линейным однородным дифференциальным уравнением n-го порядка, соответствующим (отвечающим) неоднородному уравнению (1).
Свойства решений линейных однородных уравнений
1. Если 

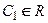
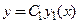

2. Если 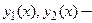

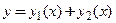

С л е д с т в и е. Если 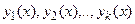

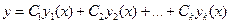

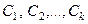
В теории линейных дифференциальных уравнений важную роль играет понятие линейной независимости системы функций на интервале.
Функции 

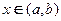

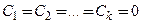
В противном случае эти функции называются линейно зависимым на 
Проверку линейной независимости системы решений однородного уравнения n-го порядка удобно выполнять при помощи следующей теоремы.
Теорема 1. Чтобы решения линейного однородного уравнения n-го порядка 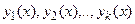

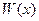
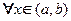
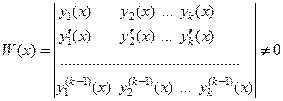
Фундаментальной системой решений линейного однородного уравненияn-го порядка на интервале 
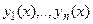

В теореме 1 сформулирован критерий фундаментальности набора (системы) n решений линейного однородного уравнения n-го порядка.
Теорема 2 (об общем решении линейного однородного уравнения). Если функции 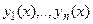


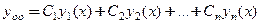
где 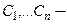
Теорема 3 (об общем решении линейного неоднородного уравнения). Если функция 
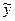
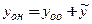
является общим решением уравнения (1).
З а м е ч а н и е (п р и н ц и п с у п е р п о з и ц и и).Если правая часть линейного неоднородного уравнения является суммой функций: 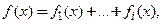
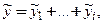
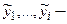
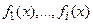
Пример 1. Проверить фундаментальность системы решений 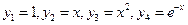
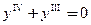
□ Непосредственной подстановкой функций 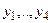
Проверим, являются ли решения уравнения 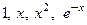
Известно, что определитель треугольной матрицы равен произведению диагональных элементов: 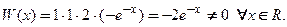
ЛИНЕЙНЫЕ ОДНОРОДНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Рассмотрим линейное дифференциальное уравнение n-го порядка
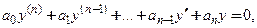
где коэффициенты 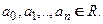
При помощи подстановки Эйлера 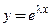
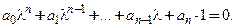
Это уравнение (7) и многочлен, корни которого следует найти, называют характеристическим уравнением и характеристическим многочленом соответственно.
Корни характеристического многочлена с действительными коэффициентами могут быть как действительными, так и комплексными числами (см. разд. 1.2.3 и 1.6.5).
Рассмотрим два случая.
1. Пусть 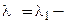
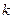
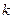
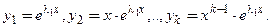
При 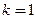
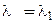
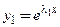
2. Пусть 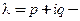
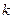
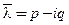
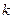
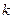
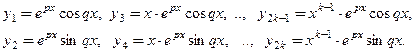
Частные решения, соответствующие разным корням характеристического уравнения (7), линейно независимы.
Как только найдено n частных линейно независимых решений, по теореме 2 можно написать общее решение в виде их линейной комбинации.
Алгоритм 1 решения линейного однородного уравнения с постоянными коэффициентами
1. Составить характеристическое уравнение (7).
2. Найти все корни уравнения (7) и определить их кратности.
3. Для каждого найденного корня написать соответствующие частные решения по
формулам (8) или (9).
4. Составить фундаментальную систему решений и записать общее решение по формуле (4).
Линейные дифференциальные уравнения высших порядков
Оговорим сразу тот факт, что нахождение решения общего аналитического вида для линейных однородных и неоднородных дифференциальных уравнений высших порядков зачастую невозможно. В основном пользуются приближенными методами решения.
Материал данной статьи представлен базовой теоретической информацией на тему решения ЛОДУ
n -ого порядка записи y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = 0 и ЛНДУ n -ого порядка записи y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = f ( x ) .
Сначала поговорим о линейных однородных дифференциальных уравнениях n -ого порядка, а затем займемся неоднородными ДУ.
Линейные однородные дифференциальные уравнения
Общее решение для линейного однородного дифференциального уравнения n -ого порядка y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = 0 при непрерывных на интервале интегрирования
X коэффициентах f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) определяет линейная комбинация y 0 = ∑ j = 1 n C j · y j , в которой y j , j = 1 , 2 , . . . , n являются линейно независимыми частными решениями ЛОДУ на X , а C j , j = 1 , 2 , . . . , n являются произвольными постоянными.
Когда тождество a 1 · y 1 + a 2 · y 2 + . . . + a n · y n ≡ 0 верно только при нулевых коэффициентах a 1 = a 2 = . . . = a n = 0 , функции y j , j = 1 , 2 , . . . , n являются линейно независимыми на неком интервале X .
Для линейно независимых функций y j , j = 1 , 2 , . . . , n определитель Вронского при любых
x из X отличен от нуля:
W ( x ) = y 1 y 2 … y n y ‘ 1 y ‘ 2 … y ‘ n y » 1 y » 2 … y » n … … … … y 1 ( n — 1 ) y 2 ( n — 1 ) … y n ( n — 1 ) ≠ 0
Тот факт, что определитель Вронского не равен нулю, возможно применять в качестве критерия линейной независимости функций на интервале.
Каким же образом определяются y j , j = 1 , 2 , . . . , n — линейно независимые частные решения линейного однородного дифференциального уравнения n -ого порядка?
В большинстве случаев данные функции возможно подобрать, используя стандартные системы линейно независимых функций:
1 ) 1 , x , x 2 , . . . , x n 2 ) e k 1 · x , e k 2 · x , . . . , e k n · x 3 ) e k 1 · x , x · e k 1 · x , . . . , x n 1 · e k 1 · x , e k 2 · x , x · e k 2 · x , . . . , x n 2 · e k 2 · x , . . . e k p · x , x · e k p · x , . . . , x n p · e k p · x
Когда подобраны все n линейно независимые частные решения y j , j = 1 , 2 , . . . , n , возможно составить общее решение линейного однородного дифференциального уравнения n -ого порядка y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = 0 — оно будет иметь запись y 0 = ∑ j = 1 n C j · y j . Когда подобраны только несколько линейно независимых частных решений, мы можем понизить степень заданного уравнения при помощи замены. Детально этот пункт мы не будем рассматривать, в случае необходимости следует изучить дополнительные материалы по теме.
Линейные неоднородные дифференциальные уравнения
Приступим к рассмотрению линейных неоднородных дифференциальных уравнений n -ого порядка записи y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = f ( x ) .
Общее решение на интервале X линейного неоднородного дифференциального уравнения порядка n записи y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = f ( x ) при непрерывных на интервале интегрирования X коэффициентах f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) и непрерывной функции f ( x ) определяется как сумма общего решения y 0 соответствующего ЛОДУ и некоторого частного решения y
заданного неоднородного уравнения: y = y 0 + y
Нахождение y 0 — общего решения соответствующего ЛОДУ n -ого порядка — было рассмотрено выше. Остается разобрать, как находится y
— частное решение линейного неоднородного дифференциального уравнения n -ого порядка.
Иногда некое частное решение y
бывает достаточно явным, то есть его возможно подобрать. Когда
y
подобрать затруднительно, при этом определены n линейно независимых частных решений y j , j = 1 , 2 , . . . , n соответствующего ЛОДУ, общее решение исходного ЛНДУ n -ого порядка возможно определить при помощи метода вариации произвольных постоянных.
В таком случае общее решение линейного неоднородного дифференциального уравнения y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = f ( x ) определяется как y = ∑ j = 1 n C j ( x ) · y j , а функции C 1 ( x ) , C 2 ( x ) , … , C n ( x ) находятся интегрированием после решения системы уравнений:
∑ j = 1 n C j ‘ ( x ) · y j = 0 ∑ j = 1 n C j ‘ ( x ) · y ‘ j = 0 ∑ j = 1 n C j ‘ ( x ) · y » j = 0 … ∑ j = 1 n C j ‘ ( x ) · y j ( n — 2 ) = 0 ∑ j = 1 n C j ‘ ( x ) · y j ( n — 1 ) = 0
http://helpiks.org/8-17881.html
http://zaochnik.com/spravochnik/matematika/differentsialnye-uravnenija/linejnye-differentsialnye-uravnenija-vysshih-porja/