Связь между уравнением гиперболы и каноническим уравнением

Гипербола, ее каноническое уравнение, свойства и параметры

Гиперболой называется множество точек плоскости, для которых модуль разности расстояний до двух фиксированных точек F₁ и F₂ этой плоскости, называемых фокусами, есть величина постоянная.

Выведем каноническое уравнение гиперболы по аналогии с выводом уравнения эллипса, пользуясь теми же обозначениями.

|r₁ — r₂| = 2a, откуда 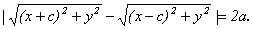Если обозначить b² = c² — a², отсюда можно получить

— каноническое уравнение гиперболы.

Эксцентриситетом гиперболы называется величина е = с / а. Директрисой D_i гиперболы, отвечающей фокусу F_i, называется прямая, расположенная в одной полуплоскости с F_i относительно оси Оу перпендикулярно оси Ох на расстоянии а / е от начала координат.

1) Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.

2) Ветви гиперболы имеют две асимптоты, определяемые уравнениями

и .

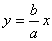
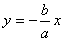
3) Наряду с гиперболой можно рассмотреть так называемую сопряженную гиперболу, определяемую каноническим уравнением

,

для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот.

4) Эксцентриситет гиперболы e > 1.

5) Отношение расстояния r_i от точки гиперболы до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы.

Параметры гиперболы; связь между ними.

Числа а и b называют вещественной и мнимой полуосями соответственно. Числа 2а и 2b – вещественной и мнимой осями.

Из определения b 2 следует, что b 2 =c 2 -a 2 , c 2 =a 2 +b 2

Если b=a, то гипербола называется равносторонней, прямоугольник гиперболы становится квадратом и его диагонали, т.е. асимптоты гиперболы, перпендикулярны. В этом случае их можно принять за новые оси координат. В результате получится «школьная» гипербола.

Эксцентриситет гиперболы. Оптическое свойство гиперболы

Эксцентриситетом гиперболы называют величину, равную отношению расстояния между фокусами к большей оси гиперболы.

E=√(1+b 2 /a 2 ), E 2 =1+b 2 /a 2 , b 2 /a 2 =E 2 -1, b/a=√(E 2 -1)

Если Е=1, то это означает, что c=a, b=0. В этом случае гипербола вырождается в отрезок на прямой Ox (-∞,-a] и [a,+ ∞).

Если E=∞, b/aè∞. Гипербола превращается в две прямые, перпендикулярные оси Ox и проходящие через вершины действительной оси гиперболы.

Если E=√2, то a=b, гипербола называется равносторонней, прямоугольник гиперболы вырождается в квадрат, асимптоты взаимно перпендикулярны.

Оптическое свойство гиперболы: свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.

Параметрическое уравнение гиперболы

a 2 ch 2 (t)/a 2 -b 2 ch 2 (t)/b 2 =1, ch 2 (t)-sh 2 (t)=1 – основное гиперболическое тождество

В этой записи x≥a, поэтому эти параметрические уравнения описывают правую ветвь гиперболы. Левую ветвь описывает система:

Сопряженная гипербола; связь между параметрами

Уравнение сопряженной гиперболы:

-x 2 /a 2 +y 2 /b 2 =1

Фокусы гиперболы располагаются на мнимой оси. (рисунок)

E=c/b, E=√(1+(a/b) 2 ), a/b=√(E 2 -1)

y=±b/a *x – уравнение асимптот сопряженной гиперболы.

Определение и вывод канонического уравнения параболы. Параметры параболы

Параболой называют множество точек плоскости, равноудаленных от фиксированной точки, называемой фокусом и фиксированной прямой, называемой директрисой.

Для вывода канонического уравнения параболы нужно построить специальную систему координат:

1. построить прямую, проходящую через F перпендикулярно директрисе и направить её от директрисы к F.

2. OF=P/2. P — параметр параболы, O – начало координат.

Точка фокуса параболы имеет координаты F (p/2, 0).

Уравнение директрисы: x=-p/2.

Точка M (x, y) принадлежит параболе, если расстояние d1 от директрисы до точки M равно расстоянию d2 от фокуса до точки M.

d1=x+p/2, d2=√((x-p/2) 2 +y 2 )

(x+p/2) 2 =(x-p/2) 2 +y 2

x 2 -px+p 2 /4+y 2 =x 2 +px+p 2 /4

y 2 =2px – каноническое уравнение параболы. Число 2P называют раствор параболы.

Очевидно, если (x0, y0) принадлежит параболе, то и (x0, -y0), симметричная ей относительно оси Ox, так же принадлежит параболе.

Поэтому парабола имеет одну ось симметрии (Ox), одну вершину – О, один фокус F (p/2, 0) и одну директрису — x=-p/2.

Параметрических уравнений у параболы нет.

Оптическое свойство параболы

Пусть из фокуса луч выпущен на параболу. Отраженный луч пройдет параллельно оси Ох.

Если из фокуса на параболу выпущен пучок лучей, то они отразятся и пройдут параллельно Ох. Если на параболу направить пучок лучей, то после отражения они попадут в точку фокуса.

Первый факт используется в осветительных приборах.

Параллельный перенос системы координат

Пусть в пространстве дана система координат XYZ и другая система координат X1Y1Z1 с соответственно параллельными и одинаково направленными осями. Пусть дана точка M (x, y, z) в данной системе координат и (x1, y1, z1) в новой. О (x0, y0, z0) – начало координат в старой системе.

Построим векторы ОМ, О1М и ОО1. Координаты точки М являются проекциями её радиус вектора, поэтому вектор ОМ совпадает с координатами в старой системе. ОО1 совпадает с координатами О1 в старой системе координат. Заметим, что проекции вектора на параллельные и одинаково направленные оси равны.

ОО1 + О1М=OM, значит это векторное равенство равносильно трем скалярным для одноименных координат:

Найдем старые координаты через новые:

Приведение уравнения кривой второго порядка к каноническому виду

Пусть уравнение кривой второго порядка не содержит, А 2 +С 2 >0

Ax 2 +Cy 2 +Dx+Ey+F=0

Выделяя полные квадраты, приведем его либо к уравнению одного из следующих видов:

(x-x0) 2 /a 2 +(y-y0) 2 /b 2 =1

(x-x0) 2 /a 2 -(y-y0) 2 /b 2 =1

-(x-x0) 2 /a 2 +(y-y0) 2 /b 2 =1

Или будет какой-нибудь частный случай.

Введем новую систему координат:

И получим систему с центром в точке O1. Тогда в новой системе координат уравнение кривой будет каноническим.

Вывод канонического уравнения гиперболы.

Дата добавления: 2015-08-31 ; просмотров: 15808 ; Нарушение авторских прав

ГИПЕРБОЛА

Определение. Гиперболой называется множество точек плоскости, разность расстояний от каждой из которых до двух данных точек плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Вывод канонического уравнения гиперболы.

F₁F₂=2с (фокусное расстояние), причем по определению 2а 2 –а 2 ), получим: .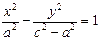

По условию а 2 –а 2 есть положительная величина, ее принято обозначать b 2 , т.е. b 2 =с 2 –а 2 (3). Тогда

(4),

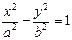
Это каноническое уравнение гиперболы. Очевидно, что гипербола – линия второго порядка.

2. Покажем, что всякая точка, координаты которой удовлетворяют уравнению (4), принадлежит гиперболе (по определению).

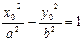
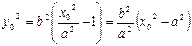
Пусть М₀(х₀; у₀) – точка, гиперболы, координаты которой удовлетворяют уравнению (4), т.е. . Отсюда . Найдем расстояния r₁=F₁М₀ и r₂=F₂М₀ (их называют левым и правым фокальными радиусами соответственно), применив формулу (3):

r₁= ,

аналогично r₂= , т.е.

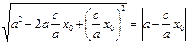
r₁= r₂= .

(Из условия (3): а 0, т.е. точка М₀ принадлежит гиперболе по определению.