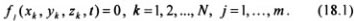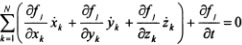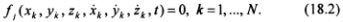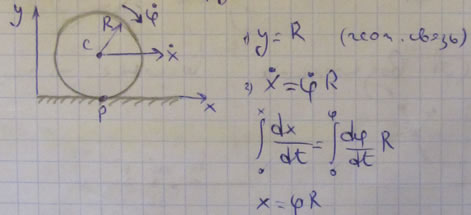Связи и их уравнения классификация связей

Связи и их уравнения классификация связей

Связи и их классификация.

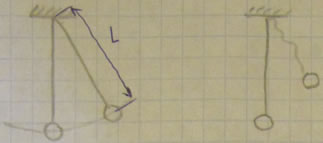
Связь называется удерживающей (двухсторонней), если она описывается уравнением (равенством). Голономную стационарную удерживающую связь, наложенную на материальную точку, можно представить в виде двух бесконечно близких одинаковых поверхностей, между которыми только и может находиться точка. Неудерживающая (односторонняя) связь описывается неравенством. Например, если математический маятник представляет собой тонкий стержень длиной l, вращающийся вокруг неподвижной оси и к свободному концу которого прикреплен груз (материальная точка), то связь для груза будет удерживающая. Если же груз прикреплен к свободному концу нерастяжимой нити длиной l. то связь будет неудерживающая, поскольку груз может находиться как на поверхности сферы радиусом l, так и внутри нее.

Механическая система, точки которой могут занимать любое положение в пространстве и иметь любые скорости, называется свободной. Например, свободной системой является космический аппарат, движущийся по орбите вокруг Земли. Его движение не ограничено другими телами и поэтому, прикладывая к аппарату соответствующие силы, можно изменять траекторию его центра масс и поворачивать аппарат вокруг центра масс. Если на координаты и скорости точек системы наложены ограничения, то система называется несвободной, а ограничения называются связями. Механические связи реализуются в виде различных устройств или тел (стержни, нити, шарниры и т. п.). Аналитически связь описывается уравнением вида: .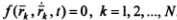

Ограничивая движение механической системы, связи действуют на ее точки посредством сил, которые называются реакциями
связей. При изучении равновесия и движения механических систем методами аналитической механики применяется принцип
освобождения (аксиома о связях). Этот принцип состоит в том, что любую систему можно рассматривать как свободную, приложив к ее точкам реакции, соответствующие отброшенным связям.

Связи называются галономными, если они описываются уравнениями вида:

Такие связи накладывают ограничения на координаты точек, а значит, на положение системы в пространстве. Это так называемые геометрические связи. Вместе с тем голономные связи накладывают ограничения и на скорости точек системы. Соответствующие условия получаются в результате дифференцирования уравнений (18.1) по времени:

Голономные связи могут описываться и дифференциальными уравнениями, однако последние обязательно должны быть интегрируемыми.

Неголономными называются связи, которые описываются уравнениями вида:

Уравнения (18.2), в отличие от уравнений голономных связей, не могут быть проинтегрированы независимо от дифференциальных уравнений движения системы. Неголономные связи накладывают ограничения (18.2) на скорости точек, поэтому их называют кинематическими.

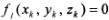
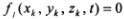
Связи подразделяются на стационарные и нестационарные в зависимости от того, входит в явном виде время в уравнение связи или нет. Связь, уравнение которой имеет вид , является голономной и стационарной. Для голономной нестационарной связи уравнение будет таким: .

Например, жесткий стержень длиной l, прикрепленный к неподвижной опоре, является стационарной связью для материальной точки, находящейся на его свободном конце. Уравнение связи в декартовой системе координат, начало которой совпадает с точкой закрепления стержня, имеет вид .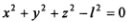

(При вращении стержня вокруг опоры точка находится на сфере радиусом l.) Если длина стержня изменяется по заданному закону, то связь является нестационарной и ее уравнение .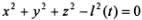

Связь называется удерживающей (двухсторонней), если она описывается уравнением (равенством). Голономную стационарную удерживающую связь, наложенную на материальную точку, можно представить в виде двух бесконечно близких одинаковых поверхностей, между которыми только и может находиться точка. Неудерживающая (односторонняя) связь описывается неравенством. Например, если математический маятник представляет собой тонкий стержень длиной l, вращающийся вокруг неподвижной оси и к свободному концу которого прикреплен груз (материальная точка), то связь для груза будет удерживающая. Если же груз прикреплен к свободному концу нерастяжимой нити длиной l. то связь будет неудерживающая, поскольку груз может находиться как на поверхности сферы радиусом l, так и внутри нее.

Из лекций:

Связи — условия, ограничивающие свободу перемещения материальной точки.

f(x,y,z,x · ,y · ,z · ,x · · ,y · · ,z · · ,t)=0

Классификация связей:

1) Геометрические связи.

2) Кинематические связи.

a) интегрируемые; (геометрические, интегрируемые кинематические = голономные)

б) неинтегрируемые; (геометрические, неинтегрируемые кинематические = неголономные)

3) Стационарная связь (склерономная).

Если t входит в уравнение явным образом, то связь нестационарная (реономная).

4) Освобождающие и неосвобождающие связи.

(неосвобождающая связь) ; (освобождающая связь)

x 2 +y 2 +z 2 =l 2 ; x 2 +y 2 +z 2 2

5) Идеальные и реальные связи.

Возможная работа — элементраная работа силы на возможном перемещении.

dA=Fdr — элементарная работа силы (F и r — векторы)

Если у какой-то связи 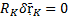(R_K тоже вектор), то связь называется идеальной.

Если вся сумма 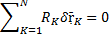, то механическая система с идеальными связями.

Реальные связи: .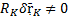

Примеры идеальных связей: внутренние связи в абсолютно твердых телах; абсолютно гладкие поверхности; шарниры без трения; нерастяжимые нити; закрепленные точки; качение без скольжения.

Примеры реальных связей: шероховатая поверхность; шарниры с трением; упругие растяжимые нити; пружины; качение с проскальзыванием.

Замечание: всякую реальную связь можно сделать идеальной.

Связи и их классификация. Идеальные связи

В аналитической механике широко используются понятия: «механическая система»; «связи», наложенные на механическую систему. Уточним эти понятия и проведём их классификацию.

Связи – материальные тела, осуществляющие ограничения, налагаемые на положения и скорости точек механической системы, которые должны выполняться при любых действующих на систему силах.

Эти ограничения записываются в виде уравнений или ограничений.

Уравнения связей – уравнения, которым в силу наложенных связей должны удовлетворять координаты точек механической системы и их скорости (первые производные от координат по времени).

Геометрические связи – связи, уравнения которых содержат только координаты точек механической системы.

Эти связи выполнены в виде тел, поверхностей, линий и т. п. Например, связь в виде некоторой поверхности описывается уравнением f(X, Y, Z) = 0.

Дифференциальные связи – связи, уравнения которых, кроме координат точек механической системы, содержат ещё первые производные от этих координат по времени.

Уравнение такой связи имеет вид

f(X, Y, Z, dX/dt, dY/dt, dZ/dt) = 0.

Голономные связи – геометрические связи и дифференциальные связи, уравнения которых можно проинтегрировать.

Неголономные связи – дифференциальные связи, уравнения которых не могут быть проинтегрированы.

Стационарные связи – связи, в уравнения которых время явно не входит.

Например, геометрическая стационарная связь в виде невесомого стержня длины l, ограничивающая перемещение материальной точки (рис. 6.11), описывается уравнением

X 2 + Y 2 + Z 2 – l 2 = 0.

Если в рассматриваемом примере (рис. 6.11) вместо стержня будет нить, длина которой с течением времени изменяется, то такая связь будет геометрически нестационарной. Эта связь описывается уравнением

X 2 + Y 2 + Z 2 – l 2 (t) = 0.

Двусторнние (удерживающие) связи – связи, допускающие возможные перемещения только в двух взаимно противоположных направлениях.

Примером такого типа связи служит, например, кулисный камень. Эти связи описываются уравнением f(X, Y, Z, t) = 0.

Односторонние (неудерживающие) связи – связи, при которых точки механической системы имеют возможные перемещения, противоположные которым не являются возможными.

К связям такого типа относится, например, шарнирно-подвижная опора. Аналитически эти связи описываются неравенствами типа f(X, Y, Z, t) ≥ 0.

Механическая система – любая совокупность материальных точек, движения которых взаимозависимы.

Голономная система – механическая система, на которую наложены голономные связи.

Неголономная система – механическая система, на которую наложена хотя бы одна неголономная связь.

Возможное перемещение системы – любая совокупность возможных перемещений точек данной механической системы, допускаемая всеми наложенными на неё связями.

Рассмотрим понятие «возможная работа силы», которое также широко применяют в аналитической механике.

Возможная (элементарная) работа силы – бесконечно малая величина, равная скалярному произведению вектора силы F на вектор возможного перемещения δS точки её приложения.

На рис. 6.12 показаны векторы F и δS.

Согласно рис. 6.12 и определению возможную работу δA(F) силы F определяют по формуле

δA(F) = F·δS = F·δS·cos(F, δS) = F·δS·cos(α).

В зависимости от величины угла α возможная работа δA(F) может быть положительной, отрицательной или равной нулю.

Рассмотрим случай, при котором под действием силы F тело совершает вращательное движение относительно оси ОХ (рис. 6.13).

При вращении тела возможную работу δA(F) силы F на возможном угловом перемещении δφ в общем случае определяют по формуле

δA(F) = ± М_ОХ(F)·δφ = ± (F·h)·δφ,

где М_ОХ(F) – момент силы F относительно оси ОХ вращения; h – плечо силы F относительно оси вращения.

Следует отметить, что при совпадении направления М_ОХ(F) и δφ возможная работа δA(F) > 0. Если направления М_ОХ(F) и δφ противоположны, то δA(F)

Дата добавления: 2015-05-30 ; просмотров: 6320 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Связи и их уравнения классификация связей

СКАЧАТЬ: 7-lekciya.zip [22,38 Kb] (cкачиваний: 40)

1. Связи и их уравнения.
2. Классификация связей.
3. Виртуальные перемещения. Виртуальная работа силы. Идеальные связи
4. Принцип возможных перемещений.
5. Общие теоремы динамики.

1. Тела, ограничивающие свободу перемещения точек данной механической системы, называется связями. В аналитической механике связи задаются уравнениями или неравенствами, в которые входят время координат всех или части точек системы и их производные по времени. В частности, для одной точки уравнение связи может иметь вид: f(x,y,z)=0 , где f(x,y,z) — заданная функция координат.
Например, связь в виде идеального стержня, ограничивающего перемещение материальной точки M(x,y,z) записывается уравнением: x2+y2+z2=l2
При свободном движении системы двух материальных точек M1 (x1,y1,z1) и M2 (x2,y2,z2) соединенных между собой идеальным стержнем. Уравнение связи из условия неизменности расстояния между точками будет иметь вид: (x2-x1)2+( y2-y1)2+( z2-z1)2=l2
Рассмотрим также две материальные точки, соединенные нерастяжимым стержнем, движущиеся в одной плоскости. Написать уравнение связи: выберем в качестве плоскости движения точки XY, тогда z1=0 и z2=0 – это уравнение связи.
Если точки, соединены стержнем, то расстояние между ними всегда l:
(x2-x1)2+( y2-y1)2=l2
Вывод: аналитическая механика позволяет описать поведение системы, минимальным количеством уравнения не вводя при этом неизвестные реакции связи. Этот метод аналитической механики нашел широкое применение в инженерной механики.
2. Связь называется голономной, если в уравнение связи входят координаты точек механической системы: f(x1,y1,z1,…xn,yn,zn,t)=0
Если в уравнении связи кроме координат входят еще и ее производные по времени и это дифференциальное уравнение не может быть проинтегрировано, то такая связь называется не голономной
Связь называют удерживающей, если она выражается математическим уравнением, и неудерживающей, если она выражается неравенством. Связь называется стационарной, если в уравнение если в уравнение связи время явно не входит, если же в в уравнение связи время входит явным образом, то связь называется нестационарной. Примером нестационарной связи является нить длина которой изменяется по заданному закону.
3. Виртуальным перемещением точки называется такое бесконечно малое элементарное перемещение d , которое допускается в рассматриваемый момент времени наложенными на точку связями, например, для связи в виде идеального стержня, виртуальное перемещение d всегда перпендикулярно радиусы сферы, по которой может перемещаться точка.
Виртуальное перемещение механической системы – это совокупность виртуальных перемещений точек этой системы.
Виртуальной работой силы называется, работа силы на виртуальном перемещении в точке ее приложения.
Связь называется идеальной если сумма работ реакций этой связи на любом виртуальном перемещении системы равна 0. Примером является шероховатая поверхность для катка, качающегося без катка, при отсутствии трения.

4. Для равновесия механической системы с идеальными м стационарными связями необходимо и достаточно чтобы сумма всех активных сил, приложенных к точкам системы была равна 0:

Доказательство необходимости: Пусть дана механическая система в равновесии. Нужно доказать, что , так как находится в равновесии, то равнодействующая сил и равнодействующая сил реакции связи приложенных к точке системы удовлетворяют условию равновесия статики: + = 0
Сообщаем системе виртуальное перемещение и умножим обе части каждого равенства на виртуальное перемещение к точке на и суммируем по всем точкам системы: , так как связи идеальные, то => => , необходимость доказана.
Докажем достаточность:
, доказать что механическая система в равновесии
Доказательство: Предположим, что при заданных условиях система не находится в равновесии, то есть при действии на систему активных сил, хотя бы одна точка точно получила перемещение .
+ ≠ 0 , так как для стационарной связи достаточное перемещение совпадает с одним из возможных перемещений.
= , ( + ) >0 суммируем ко всем точкам , так как связи идеальные => => — это противоречит условию => система находится в равновесии.
5. При движении механической системы с идеальными связями работа всех активных сил и сил инерции на любом виртуальном перемещении системы = 0.
Рассмотрим движение К-ой точки системы:
mk = +
= — mk
Мысленно зафиксируем время t и дадим системе виртуальное перемещение умножим скалярно каждое уравнение на и сложим их:

по определению идеальных связей последняя сумма равна 0 , следовательно , сумма