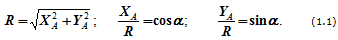Связи и реакции связей уравнения равновесия

iSopromat.ru

Связями называют тела, ограничивающие свободу перемещения рассматриваемого тела.

Реакции связей — это усилия, с которыми связи действуют на данное тело.

Тела в природе бывают свободными и несвободными. Тела, свобода перемещения которых ничем не ограничена, называются свободными.

Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.

Подробнее про связи и реакции связей смотрите в нашем видео:

Очень важно правильно расставить реакции связей, иначе написанные уравнения окажутся неверными. Ниже приведены примеры замены связей их реакциями. На рисунках 1.1–1.8 показаны примеры замены реакциями сил, расположенных в плоскости.

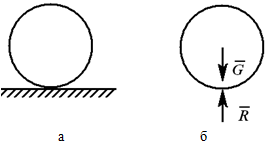
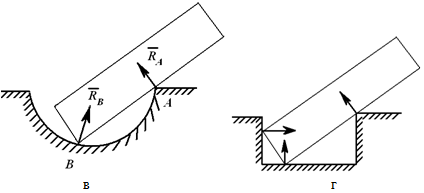
Реакция гладкой поверхности всегда направлена по нормали к этой поверхности (рисунок 1.1). Реакция «невесомого» троса (нити, цепи, стержня) всегда направлена вдоль троса (нити, цепи, стержня) (рисунок 1.2).

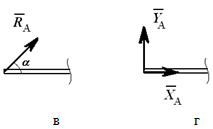
Шарнирно-неподвижная опора может изображаться по-разному (рисунок 1.3, а или 1.3, б). Она может быть заменена либо силой R с углом α (рисунок 1.3, в), либо двумя силами, например, X_A и Y_A (рисунок 1.3, г).

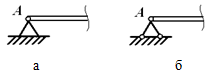
Всегда можно перейти от R и α к X_A и Y_A (и наоборот):

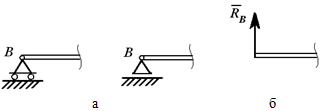
Шарнирно-подвижная опора (рисунок 1.4, а) допускает (в данном случае) горизонтальное перемещение и не допускает вертикальное. Реакция направлена по нормали к опорной поверхности (рисунок 1.4, б).

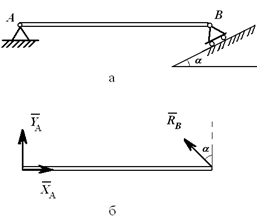
Связи шарнирно-неподвижной опоры в точке A и шарнирно-подвижной опоры в точке B отброшены (рисунок 1.5, б), их действие заменено силами X_A, Y_A и R_B.

Соединение стержня и втулки в плоскости (рисунок 1.6) – скользящая заделка. Отбросим втулку – получим действие на стержень силы R_D и момента M_D.

На рисунке 1.7, а изображена бискользящая заделка. В плоскости данная опора допускает поступательное перемещение стержня как по горизонтали, так и по вертикали, но препятствует повороту (в плоскости). Реакцией такой опоры будет момент M_C (рисунок 1.7, б).

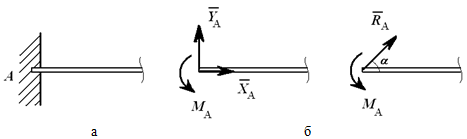
Консоль (глухая или жесткая заделка) не допускает никакого перемещения детали. Реакцией такой опоры являются неизвестная по величине и направлению сила R_A с углом α (или X_A и Y_A) и момент Μ_A (рисунок 1.8).

На рисунках 1.9 – 1.15 показаны примеры замены сил, расположенных в пространстве, их реакциями.

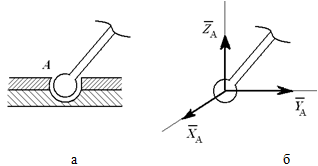
Шарнирно-неподвижная опора, или сферический шарнир (рисунок 1.9, а), заменена системой сил (рисунок 1.9, б) X_A, Y_A и Z_A, т.е. силой, неизвестной по величине и направлению.

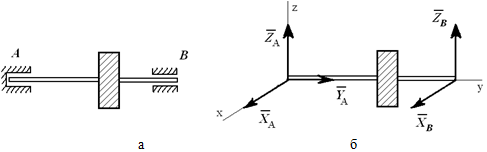
На рисунке 1.10, а показан вал, закрепленный в опорах: в точке A – подпятник или стакан, в точке B – втулка или подшипник. Действие опор заменено силами X_A, Y_A, Z_A и X_B, Z_B (рисунок 1.10, б).

На рисунках 1.11 и 1.12 приведены примеры замены различных связей их реакциями.

Методы определения реакций опор твердого тела

Как определить реакции опор твердого тела

Чтобы определить реакции опор твердого тела нужно выполнить следующие шаги.

• Вместо связей в опорах приложить силы реакций.
• Если есть распределенная нагрузка, то заменить ее равнодействующей силой. Ее величина равна площади эпюры нагрузки. Точка приложения находится в центре тяжести эпюры. Так для равномерно распределенной на отрезке нагрузки, ее равнодействующая приложена к середине этого отрезка.
• Выбрать систему координат. Ее начало желательно выбрать в точке крепления одной из опор.
• Составить уравнения равновесия.
  Векторная сумма всех действующих на тело сил (включая реакции опор) равна нулю:
  (1) .
  Векторная сумма моментов этих сил относительно начала системы координат O равна нулю:
  (2) .
• Составить проекции уравнений равновесия (1) и (2) на оси системы координат.
  Суммы проекций сил на оси координат равны нулю:
  (1.x) ;
  (1.y) ;
  (1.z) .
  Суммы моментов сил относительно координатных осей равны нулю:
  (2.x) ;
  (2.y) ;
  (2.z) .
• Для трехмерной задачи мы получим систему из шести уравнений, решая которую, определяем шесть неизвестных проекций реакций опор.
• Для плоской задачи, в которой все действующие силы направлены вдоль осей x и y, получаем три уравнения равновесия: (1.x), (1.y) и (2.z). Из них определяем три неизвестные проекции реакций опор.
• Для упрощения расчетов, иногда бывает полезно спроектировать уравнения равновесия (1) и (2) на другие оси, и составить дополнительные уравнения для моментов относительно других точек. См. Три формы уравнений равновесия твердого тела
• Если полученная система не имеет решения, то при такой схеме закрепления тела равновесие не возможно.
• Если число неизвестных превышает число линейно независимых уравнений, то задача имеет бесконечно много решений, она статически неопределима. Такую задачу можно решить только методами сопротивления материалов. Пример: плоское тело с четырьмя опорами.

Далее мы рассмотрим вопросы, связанные с определением реакций опор твердого тела более подробно и разберем пример решения задачи.

Методы определения реакций опор твердого тела

Рассмотрим некоторое твердое тело, на которое действуют заданные внешние силы. Пусть оно определенным образом закреплено в некоторых точках – опорах, и находится в состоянии равновесия. Эти точки закрепления также называются связями. Это могут быть шарниры, заделки, поверхности и т. п.

Отбросим опоры, и приложим вместо них силы. Они называются силами реакций опор. Их направления определяются устройствами соответствующих опор. В некоторых опорах реакции возникают в виде пары сил, которые задаются значением момента пары. Нам нужно найти такие значения сил реакций, чтобы при их действии на тело, оно покоилось, как это происходит в закрепленном состоянии.

Воспользуемся двумя законами, которые выполняются, если тело находится в покое.
1) Векторная сумма всех действующих на тело внешних сил равна нулю:
(M.1) .
2) Векторная сумма моментов всех внешних сил относительно любой точки O равна нулю:
(M.2) .
Эти законы называются уравнениями равновесия. В них также включены силы (пары сил) реакций опор.

Самый простой способ составления уравнений равновесия

Разберем самый простой способ составления уравнений равновесия. С его помощью можно гарантированно получить значения сил реакций опор или определить, что схема закрепления тела в опорах является статически неопределимой.

Выберем прямоугольную систему координат с началом в любой точке. Часто за начало системы координат удобно выбрать точку крепления одной из опор, но это не обязательно. Итак, пусть мы выбрали систему координат Oxyz с началом в точке O .

Спроектируем (M.1) на оси этой системы. В результате мы получим три уравнения, связывающие проекции сил на оси xyz :
(M.1.x) ;
(M.1.y) ;
(M.1.z) .
Здесь – n сил, действующих на тело. В их состав также включены и силы реакций опор.

Составим уравнения равновесия (M.2) для моментов, относительно осей Ox , Oy , Oz системы координат:
(M.2.x) ;
(M.2.y) ;
(M.2.z) .
Заметим, что эти уравнения являются проекциями векторного уравнения (M.2) на оси Ox , Oy и Oz .

Уравнения (M.1.x), (M.1.y), (M.1.z) и (M.2.x), (M.2.y), (M.2.z) представляют собой полную систему уравнений равновесия твердого тела. Если мы попытаемся добавить сюда еще одно уравнение, то оно будет являться линейной комбинацией уже существующих уравнений, и никак не повлияет на численные значения определяемых реакций опор. Например, мы можем выбрать еще одну ось, и спроектировать на нее уравнение (M.1) для сил. Или мы можем составить уравнение для моментов (M.2) относительно другой точки, отличной от начала координат. В результате получим дополнительные уравнения, но число линейно независимых уравнений от этого не изменится.

Таким образом, для одного тела, методами статики, мы можем составить максимум шесть независимых уравнений равновесия. В некоторых случаях их число может быть еще меньше.

Так, в случае плоской системы сил, у нас будет всего три независимых уравнения. Чтобы в этом убедиться, выберем систему координат, у которой оси Ox и Oy лежат в плоскости действия сил. Ось Oz перпендикулярна. Тогда проекции всех сил на ось Oz равны нулю. Поэтому уравнение (M.1.z) выполняется автоматически, и его можно вычеркнуть. В уравнениях (M.2.x) и (M.2.y) все силы или пересекают оси Ox и Oy, или параллельны им. Поэтому их моменты относительно этих осей равны нулю. Тогда и уравнения (M.2.x) и (M.2.y) выполняется автоматически. Их также можно вычеркнуть. Остаются три уравнения равновесия (M.1.x), (M.1.y) и (M.2.z).

Неизвестными в уравнениях равновесия являются проекции сил реакций опор на оси координат, или проекции пар сил. При решении этих уравнений могут возникнуть следующие случаи.

1. Число неизвестных совпадает с числом линейно независимых уравнений. Тогда задача статически определима, и мы можем получить значения неизвестных реакций, решив линейную систему уравнений.
2. Число неизвестных меньше числа линейно независимых уравнений и система не имеет решений – при такой схеме закрепления тела равновесие не возможно.
3. Число неизвестных превышает число независимых уравнений – система имеет бесконечное множество решений. Выбрать единственное решение, используя только методы статики, нельзя. Задача является статически неопределимой. Такие задачи решаются методами сопротивления материалов. Например, если балка имеет четыре опоры, то у нас минимум четыре неизвестные величины и три уравнения равновесия (для плоской системы сил). В этом случае, для определения реакций, необходимо учитывать возникающие в балке деформации и напряжения.

Эффективные способы составления уравнений равновесия

Уравнений (M.1) и (M.2) достаточно для определения опорных реакций, но иногда бывает удобным дополнить их другими уравнениями, из которых можно определить реакции более легким способом.

Один из способов заключается в соответствующем выборе начала системы координат. Так, если за ее начало взять точку крепления одной из опор тела, то сила реакции в этой опоре будет пересекать начало координат, и поэтому ее момент будет равен нулю (это не относится к паре сил). Тогда компоненты этих сил реакций не будут входить в уравнения для моментов (M.2.x), (M.2.y), (M.2.z).

Спроектировав уравнение равновесия для сил на ось AD, находим реакцию R_B

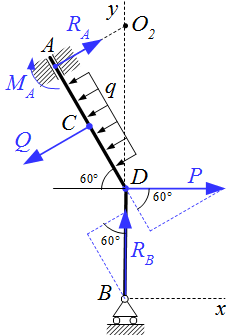
Уравнения (М.1.x) – (М.1.z) представляют собой проекции векторного уравнения (М.1) на оси координат. Но это уравнение можно спроектировать на любую ось. Тогда в него не войдут силы, перпендикулярные выбранной оси. На рисунке слева изображено тело ADB. Реакция в скользящей заделке A состоит из силы R_A и пары сил с моментом M_A; в опоре на катках B – из силы R_B. Для определения только одной реакции R_B, мы можем спроектировать уравнение для сил на ось AD (см. рисунок). Поскольку реакция перпендикулярна этой оси, то ее проекция на AD равна нулю. Равномерно распределенная нагрузка q, и ее равнодействующая Q также перпендикулярна AD. В результате получим уравнение, содержащее только одну реакцию R_B:
;
;
.
Отсюда сразу определяем R_B:
.

Поскольку в равновесии сумма моментов сил равна нулю относительно любой точки, то можно выбрать дополнительную точку, и относительно нее составить уравнение для моментов:
.
Число линейно независимых уравнений при этом не изменится, но мы можем дополнить систему более простым уравнением. См. Три формы уравнений равновесия твердого тела.

Вернемся к нашему примеру ⇑. Пусть нам нужно определить только момент . Тогда можно выбрать точку O₂ на пересечении линий действия сил и . Поскольку эти силы пересекают O₂, то их моменты относительно этой точки равны нулю. Составим уравнение для моментов:
.
Спроектируем его на ось z, перпендикулярную плоскости рисунка:
;
;
.
Отсюда находим :
.

Для трехмерного распределения сил, уравнения (M.2.x), (M.2.y) и (M.2.z) являются проекциями векторного уравнения для моментов (M.2) на оси координат. Но это уравнение можно спроектировать на любую ось, не обязательно параллельной одной из осей системы координат, как мы делали для сил.

Далее приводится подробно разобранный пример решения задачи, в котором требуемая реакция определяется из одного уравнения за счет соответствующего выбора оси, относительно которой вычисляются суммы моментов сил.
Определение реакций опор твердого тела — решение задачи

Автор: Олег Одинцов . Опубликовано: 30-10-2017 Изменено: 06-01-2022

Техническая механика

Теоретическая механика

Принцип освобождаемости.
Связи и реакции связей

Как уже упоминалось в предыдущих статьях, статика изучает условия, при которых тела и материальные точки находятся в состоянии равновесия. Казалось бы, благодаря аксиомам статики, описывающим основные свойства силового взаимодействия между телами, решение задач равновесия тел не должно представлять трудностей — неизвестные силы можно найти, зная, что они должны уравновешиваться известными силами, отсюда и ключ к решению.
Тем не менее, основная сложность при расчетах заключается в том, что силы — векторные величины, и для решения задач необходимо знать не только их скалярные размерности (модули) , но и направление в пространстве, а также точки приложения. В результате получается, что каждая неизвестная сила содержит три вопроса: куда она направлена, где приложена, и какова ее величина?

Исключить некоторые неизвестные составляющие сил помогает анализ связей между телами. Как мы уже знаем, все тела и материальные точки подразделяются на свободные и связанные (несвободные) . В статике чаще всего приходится решать задачи, в которых рассматривается условие равновесия связанных тел, т. е. имеющих некоторые (или полные) ограничения на перемещение в пространстве относительно других тел.
Эти ограничения называются связями.

Примерами связей, ограничивающих перемещение тела, может послужить поверхность или какая-либо опора, на которой лежит тело, жесткая заделка части тела в массив, исключающая любое его перемещение, а также гибкие и шарнирные связи, частично ограничивающие возможность тела перемещаться в пространстве.
Анализ таких связей позволяет понять, какие силовые факторы возникают в них при противодействии перемещению связанного тела. Эти силовые факторы называют силами реакции или реакциями связей (обычно их называют просто реакциями) .
Силы, которыми тело воздействует (давит) на связи называют силами давления.
Следует отметить, что силы реакций и давлений приложены к различным телам, поэтому не представляют собой систему сил.

Силы, действующие на любое тело можно разделить на активные и реактивные.
Активные силы стремятся перемещать тело, к которому они приложены, в пространстве, а реактивные силы — препятствуют этому перемещению. Силы реакции связей относятся к реактивным силам.
Принципиальное отличие активных сил от реактивных заключается в том, что величина реактивных сил зависит от величины активных сил, но не наоборот. Активные силы часто называют нагрузками.

При решении большинства задач статики несвободное тело условно изображают как свободное с помощью так называемого принципа освобождаемости, который формулируется следующим образом: всякое несвободное (связанное) тело можно рассматривать как свободное, если отбросить связи и заменить их реакциями.

Типичные связи тел и их реакции

Рассмотрим наиболее часто встречающиеся связи, а также возникающие в них реакции при приложении нагрузок.

Идеально гладкая плоскость

Реакция идеально гладкой плоскости направлена перпендикулярно опорной плоскости в сторону тела, так как такая связь не дает телу перемещаться лишь в одном направлении — в сторону опорной плоскости, т. е. перпендикулярно ей (см. рисунок 1,а) .
Если же тело находится на наклонной плоскости, то силу его тяжести G можно разложить на две составляющие, из которых одна будет направлена параллельно плоскости (Xa), другая — перпендикулярно ей (Ya). При этом первая сила будет стремиться передвигать тело по плоскости в сторону уклона, а вторая — прижимать его к плоскости (см. рисунок 1,б) .
Реакция наклонной плоскости будет равна по модулю составляющей, перпендикулярной плоскости и направлена в сторону, противоположную этой составляющей, уравновешивая ее. Если тело касается плоскости одной точкой (например, шар или угол) , то реакция будет приложена к этой точке тела.
В других случаях, когда тело касается плоскости некоторой поверхностью, имеет место взаимодействие посредством нагрузки, распределенной по этой поверхности (распределенной нагрузки).

Идеально гладкая поверхность

Идеально гладкая поверхность (отличается от плоскости криволинейностью) реагирует перпендикулярно касательной плоскости, т. е. по нормали к опорной поверхности в сторону тела, так как нормаль — единственное направление перемещения тела, которое не допускает данная связь (см. рисунок 1,в) .

Закрепленная точка или ребро угла

В случае, если перемещение тела ограничивается закрепленной точкой или ребром угла, реакция связи направлена по нормали к поверхности идеально гладкого тела в сторону тела, так как нормаль к поверхности тела — единственное направление, движение в котором ограничено этим видом связи (см. рисунок 1,г) .

Гибкая связь

Реакция гибкой связи (гибкая нить) не дает телу удаляться от точки подвеса и поэтому направлена вдоль связи от тела к точке подвеса, т. е. известны точка приложения реакции гибкой связи и ее направление. На рисунке 2 изображена гибкая связь, служащая связующим звеном между двумя стержнями и телом.

В конструкциях широкое распространение имеют связи, которые называются шарнирами. Шарнир представляет собой подвижное соединение двух тел (деталей) , допускающее только вращение вокруг общей точки (шаровой шарнир) или вокруг общей оси (цилиндрический шарнир) . Рассмотрим, какие реакции возникают при связывании тела с помощью шарниров.

Идеально гладкий цилиндрический шарнир

При связывании тела цилиндрическим шарниром возможно его перемещение вдоль оси шарнира и вращение относительно этой оси. Реакция цилиндрического шарнира расположена в плоскости, перпендикулярной его оси и пересекает эту ось. Направление вектора реакции шарнира на этой плоскости зависит от направления вектора нагрузки.
Примером цилиндрического шарнира может послужить обыкновенный подшипник качения.

Идеально гладкий шаровой шарнир

В этом случае заранее известно лишь то, что реакция проходит через центр шарнира, так как тело, связанное шаровым шарниром, может поворачиваться в любом направлении относительно оси шарнира, но не может совершать никаких линейных перемещений в пространстве, т. е. удаляться от центра шарнира или приближаться к нему.

Идеально гладкий подпятник

Подпятник можно рассматривать, как сочетание цилиндрического шарнира и опорной плоскости, поэтому реакция подпятника считается состоящей из двух составляющих: X_a и Y_a . При этом одна из реакций будет направлена вдоль нормали к опоре в сторону тела (как у опорной плоскости), другая — перпендикулярно оси подпятника (как у цилиндрического шарнира) .
Полная реакция подпятника будет равна векторной сумме этих составляющих: R_a = X_a +Y_a.

Стержень, закрепленный шарнирно

Стержень, закрепленный двумя концами в идеально гладких шарнирах и нагруженный концами (рис. 2) , реагирует только по линии, соединяющей оси шарниров, т. е. вдоль своей оси (согласно III аксиоме статики) . При этом реакция стержня может быть направлена и к центру шарнира (точке крепления) , и от него (в зависимости от направления нагрузки) , поскольку этот вид связи удерживает тело на фиксированном расстоянии, не позволяя ему удаляться или приближаться. Этим стержень принципиально отличается от гибкой связи, у которой реакция всегда направлена от точки крепления в сторону связи (гибкая связь удерживает тело только от удаления, не запрещая ему приближаться к точке крепления) .

Жесткая заделка

Этот вид связи полностью лишает тело возможности перемещаться в любом направлении и вращаться относительно какой-либо оси или точки.
При жесткой заделке тела ( рис. 3 ) в опоре возникает не только реактивная сила R_A , но и реактивный момент М_A .
Жесткая заделка является «темной лошадкой» при вычислениях, поскольку изначально ни направление реакций, ни их величина неизвестны, особенно если нагрузка представлена системой сил. Тем не менее, используя разложение активных сил на составляющие, последовательно можно определить и реактивную силу R_A , и реактивный момент M_A , действующие в жесткой заделке.
В случае, если тело связано не только жесткой заделкой, но и другим видом связи, задача становится нерешимой обычными методами статики, поскольку неизвестных реакций больше, чем возможное количество уравнений равновесия.

Пример решения задачи по определению реакций жесткой заделки приведен на этой странице.

Понятие бруса и балки в технической механике

В статике нередко приходится решать задачи на условие равновесия элементов конструкций, называемых брусьями.
Брусом принято считать твердое тело, у которого длина значительное больше поперечных размеров. Осью бруса считается геометрическое место (множество) центров тяжести всех поперечных сечений этого бруса.
Брус с прямолинейной осью, положенный на опоры и изгибаемый приложенными к нему нагрузками, называют балкой.