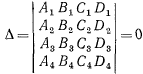Связка плоскостей и ее уравнение

Связка плоскостей

Теорема 1. Для того чтобы четыре плоскости, заданные своими общими уравнениями относительно ПДСК принадлежали одной связке, необходимо и достаточно, чтобы

Теорема 2. Для того чтобы плоскость принадлежала связке плоскостей, необходимо и достаточно, чтобы левая часть ее общего уравнения являлась линейной комбинацией левых частей уравнения плоскостей, образующих связку.
Замечание: предполагается, что плоскости, образующие связку не принадлежат одному пучку.

Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:

Лекция № 10

Ссылки

Глава IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

§12. УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ

12.1. Основные понятия

Поверхность и ее уравнение

Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке О₁ есть геометрическое место всех точек пространства, находящихся от точки O₁ на расстоянии R.

Прямоугольная система координат Oxyz в пространстве позволяет установить взаимно однозначное соответствие между точками простран­ства и тройками чисел х, у и z — их координатами. Свойство, общее всем точкам поверхности, можно записать в виде уравнения, связывающего ко­ординаты всех точек поверхности.

Уравнением данной поверхности в прямоугольной системе координат Oxyz называется такое уравнение F(x, у, z) = 0 с тремя переменны­ми х, у и z, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные х, у и z в уравнении поверхности называ­ются текущими координатами точек поверхности.

Уравнение поверхности позволяет изучение геометрических свойств поверхности заменить исследованием его уравнения. Так, для того, чтобы узнать, лежит ли точка M₁(x₁;y₁;z₁) на данной поверхности, достаточно подстав и ть координаты точки M₁ в уравнение поверхности вместо пере­менных: если эти координаты удовлетворяют уравнению, то точка лежит на поверхности, если не удовлетворяют — не лежит.

Найдем уравнение сферы радиуса R с центром в точке O₁(x₀;y₀;z₀). Согласно определению сферы расстояние любой ее точки М(х; у; z) от центра O₁(x₀;y₀;z₀) равно радиусу R, т. е. O₁M= R. Но , где . Следовательно,

Это и есть искомое уравнение сферы. Ему удовлетворяют координаты лю­бой ее точки и не удовлетворяют координаты точек, не лежащих на данной сфере.

Если центр сферы Ο₁ совпадает с началом координат, то уравнение сферы принимает вид .

Если же дано уравнение вида F(x;y;z) = 0 , то оно, вообще говоря, определяет в пространстве некоторую поверхность.

Выражение «вообще говоря» означает, что в отдельных случаях уравнение F(x; y; z)=0 может определять не поверхность, а точку, линию или вовсе не определять никакой геометрический образ. Говорят, «поверхность вырождается».

Так, уравнению не удовлетворяют никакие дей­ствительные значения х, у, z. Уравнению удовлетворяют лишь координаты точек, лежащих на оси Ох (из уравнения следует: у = 0, z = 0, а х — любое число).

Итак, поверхность в пространстве можно задать геометрически и ана­литически. Отсюда вытекает постановка двух основных задач:

1. Дана поверхность как геометрическое место точек. Найти уравнение этой поверхности.

2. Дано уравнение F(x;y;z) = 0. Исследовать форму поверхности, определяемой этим уравнением.

Уравнения линии в пространстве

Линию в пространстве можно рассматривать как линию пересечения двух поверхностей (см. рис. 66) или как геометрическое место точек, об­щих двум поверхностям.

Если и — уравнения двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют системе двух уравнений с тремя неизвестными:

(12.1)

Сравнения системы (12.1) называются уравнениями линии в пространстве. Например, есть уравнения оси Ох.

Линию в пространстве можно рассматривать как траекторию движения точки (см. рис. 67). В этом случае ее задают векторным уравнением

(12.2)

или параметрическими уравнениями

проекций вектора (12.2) на оси координат.

Например, параметрические уравнения винтовой линии имеют вид

Если точка Μ равномерно движется по образующей кругового цилиндра, а сам цилиндр равномерно вращается вокруг оси, то точка Μ описывает винтовую линию (см. рис. 68).

12.2. Уравнения плоскости в пространстве

Простейшей поверхностью является плоскость. Плоскость в пространстве Oxyz можно задать разными способами. Каждому из них соответствует определенный вид ее уравнения.

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

Пусть в пространстве Oxyz плоскость Q задана точкой и вектором , перпендикулярным этой плоскости (см. рис. 69). Выведем уравнение плоскости Q. Возьмем на ней произвольную точку и составим вектор . При любом расположении точки Μ на плоскости Q векторы и взаимно перпендикулярны, поэтому их скалярное произведение равно нулю: , т. е.

(12.3)

Координаты любой точки плоскости Q удовлетворяют уравнению (12.3), координаты точек, не лежащих на плоскости Q, этому уравнению не удовлетворяют (для них ).

Уравнение (12.3) называется уравнением плоскости, проходящей через данную точку перпендикулярно вектору . Оно первой степени относительно текущих координат x, y, z. Вектор называется нормальным вектором плоскости.

Придавая коэффициентам А, В и С уравнения (12.3) различные значения, можно получить уравнение любой плоскости, проходящей череp точку . Совокупность плоскостей, проходящих через данную точку, называется связкой плоскостей, а уравнение (12.3) — уравнением связки плоскостей.

Общее уравнение плоскости

Рассмотрим общее уравнение первой степени с тремя переменными х, у и z:

(12.4)

Полагая, что по крайней мере один из коэффициентов А, В или С не равен нулю, например , перепишем уравнение (12.4) в виде

(12.5)

Сравнивая уравнение (12.5) с уравнением (12.3), видим, что уравнения (12.4) и (12.5) являются уравнением плоскости с нормальным вектором , проходящей через точку .

Итак, уравнение (12.4) определяет в системе координат Oxyz некоторую плоскость. Уравнение (12.4) называется общим уравнением плоскости.

Частные случаи общего уравнения плоскости:

1. Если D = 0, то оно принимает вид . Этому уравнению удовлетворяет точка . Следовательно, в этом случае плос­кость проходит через начало координат.

2. Если С = 0, то имеем уравнение . Нормальный вектор перпендикулярен оси Οz. Следовательно, плоскость параллельна оси Οz; если B = 0 — параллельна оси Оу, А = 0 — параллельна оси Ох.

3. Если С = D = 0, то плоскость проходит через параллельно оси Οz, т. е. плоскость проходит через ось Οz. Аналогично, уравнениям и отвечают плоскости, проходящие соответственно через оси Ох и Оу.

4. Если А = В = 0, то уравнение (12.4) принимает вид , т. е. Плоскость параллельна плоскости Оху. Аналогично, уравнениям и отвечают плоскости, соответственно параллельные плоскостям Oyz и Οxz.

5. Если A = B = D = 0, то уравнение (12.4) примет вид , т. е. z = 0. Это уравнение плоскости Оху. Аналогично: у = 0 — уравнение плоскости Οxz; x = О — уравнение плоскости Oyz.

Уравнение плоскости, проходящей через три данные точки

Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Найдем уравнение плоскости Q, проходящей через три данные точки M₁(x₁;y₁;z₁), М₂(x₂;y₂;z₂) и М₃(х₃,y₃,z₃), не лежащие на одной прямой.

Возьмем на плоскости произвольную точку M(x;y;z) и составим век­торы , , . Эти векторы лежат на плоскости Q, следовательно, они компланарны. Используем условие компланарнос­ти трех векторов (их смешанное произведение равно нулю), получаем , т. е.

(12.6)

Уравнение (12.6) есть уравнение плоскости, проходящей через три данные точки.

Уравнение плоскости в отрезках

Пусть плоскость отсекает на осях Ох, Оу и Оz соответственно отрезки a, b и c, т. е. проходит через три точки A(a;0;0), B(0;b;0) и C(0;0;c) (см.рис. 70). Подставляя координаты этих точек в уравнение (12.6), получаем

Раскрыв определитель, имеем , т. е. или

(12.7)

Уравнение (12.7) называется уравнением плоскости в отрезках на осях. Им удобно пользоваться при построении плоскости.

Нормальное уравнение плоскости

Положение плоскости Q вполне определяется заданием единичного вектора , имеющего направление перпендикуляра ОК, опущенного на

плоскость из начала координат, и длиной p этого перпендикуляра (см. рис. 71).

Пусть ОК = p, а α, β, g — углы, образованные единичным вектором ё с осями Ох, Оу и Οz. Тогда . Возьмем на плоскости произвольную точку М(х; у; z) и соединим ее с началом координат. Образуем вектор . При любом положении точки Μ на плоскости Q проекция радиус-вектора на направление вектора всегда равно р: , т. е. или

(12.8)

Уравнение (12.8) называется нормальным уравнением плоскости в векторной форме. Зная координаты векторов f и e , уравнение (12.8) перепишем в виде

(12.9)

Уравнение (12.9) называется нормальным уравнением плоскости в координатной форме.

Отметим, что общее уравнение плоскости (12.4) можно привести к нормальному уравнению (12.9) так, как это делалось для уравнения прямой на плоскости. А именно: умножить обе части уравнения (12.4) на норми­рующий множитель , где знак берется противоположным знаку свободного члена D общего уравнения плоскости.

12.3. Плоскость. Основные задачи

Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей

Пусть заданы две плоскости Q₁ и Q₂:

Под углом между плоскостями Q₁ и Q₂ понимается один из двугран­ных углов, образованных этими плоскостями.

Угол j между нормальными векторами и плоскостей Q₁ и Q₂ равен одному из этих углов (см. рис. 72).

Для нахождения острого угла следует взять модуль правой части.

Если плоскости Q₁ и Q₂ перпендикулярны (см. рис. 73, а), то таковы же их нормали, т. е. (и наоборот). Но тогда , т. е. . Полученное равенство есть условие перпендикулярности двух плоскостей Q₁ и Q₂.

Если плоскости Q₁ и Q₂ параллельны (см. рис. 73, б), то будут параллельны и их нормали и (и наоборот). Но тогда, как известно координаты векторов пропорциональны: . Это и есть уcловиє параллельности двух плоскостей Q₁ и Q₂.

Расстояние от точки до плоскости

Пусть задана точка и плоскость Q своим уравнением . Расстояние d от точки до плоскости Q находится по формуле

Вывод этой формулы такой же, как вывод формулы расстояния от точки до прямой .

Расстояние d от точки M₀ до плоскости Q равно модулю проекции вектора , где — произвольная точка плоскости Q, на направление нормального вектора (см. рис. 74). Следовательно,

А так как точка принадлежит плоскости Q, то

Поэтому . Отметим, что если плоскость Q задана уравнением , то расстояние от точки до плоскости Q может быть найдено по формуле

Уравнение плоскости, проходящей через три заданные точки

— уравнение плоскости, проходящей через три заданные точки.

Нормальное уравнение плоскости

Пусть задана плоскость α и пусть — единичный, вектор нормали к плоскости α проведенный из начала координат. Обозначим р — расстояние от начала координат до плоскости α.

Для любой точки М(х,у,z) α

=p

Так как = (х,у,z),

= (cosα, cosβ, cosγ), где α, β, γ – углы, образованные вектором соответственно с осями OX, OY и 0Z, то отсюда получаем

– нормальное равнение плоскости.

Расстояние от точки до плоскости

Обозначим через d расстояние от точки M₀(x₀,y₀,z₀) до плоскости α, заданной общим уравнением вида (*).

Взаимное расположение двух плоскостей

Пусть плоскости α₁ и α₂ заданы уравнениями:

Теорема. Тогда и только тогда плоскости α₁ и α₂:

2) параллельны и различны, когда

A₁=λA₂, В₁=λВ₂, С₁=λС₂, D₁ λD₂;

3)пересекаются, когда коэффициенты А₁, В₁, С₁ не пропорциональны коэффициентам А₂, В₂, С₂

Пучок и связка плоскостей

Пучком плоскостей называется множество всех плоскостей, проходящих через некоторую прямую, называемую осью пучка.

Пусть в системе координат ОХУZ заданы две пересе-кающиеся плоскости α₁ и α₂ .

Тогда уравнение пучка имеет вид

А₁х + B₁y + C₁z + D₁ + λ(A₂x + B₂y + C₂z + D₂) = 0, где λ R.

Связкой плоскостей называется множество всех плоскостей, проходящих через некоторую точку, называемую центром связки. Если S₀ (x₀,y₀,z₀) – центр связки, то уравнение связки с центром в точке S₀ имеет вид

где А, В и С – произвольные действительные числа, одновременно не равные нулю.

Угол между двумя плоскостями

Пусть даны плоскости α₁ и α₂ своими общими уравнениями. Тогда под углом φ между плоскостями α₁ и α₂ понимают наименьший угол, на который надо повернуть одну из плоскостей до ее совпадения с другой плоскостью. Поэтому . Очевидно, что либо φ=( ^, ), либо φ= (- ^, ), где и — нормальные векторы плоскостей α₁ и α₂ соответственно. В любом случае

В частности, если φ = π/2, то

— условие перпендикулярности двух плоскостей.

IV ПРЯМАЯ В ПРОСТРАНСТВЕ.

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ

Уравнение прямой в пространстве

Очевидно, что прямую в пространстве можно задать как линию пересечения двух плоскостей α₁ и α₂. Тогда в произвольной афинной системе координат прямая задается системой двух линейных уравнений

(1)

— общее уравнение прямой или уравнение прямой в общем виде.

Пусть l – прямая. Тогда ее положение в пространстве однозначно определяется заданием ее направляющего вектора =(m,n,р) и точкой М₀(х₀,у₀,z₀), через которую прямая проходит. Возьмем произвольную точку М(х,у,z) l. Тогда и, значит,

Переходя к координатам, получим

— параметрические уравнение прямой.

Выражая параметр t, получим

— каноническое уравнение прямой, проходящей через точку М₀(х₀ y₀,z₀) параллельно вектору =(m,m,р).

Последнее уравнение равносильно

— общее уравнение прямой.

— уравнение прямой, проходящей через две заданные точки.

Наоборот, пусть задано общее уравнение прямой.

— каноническое уравнение прямой.

Взаимное расположение двух прямых в пространстве

Пусть прямые l₁ и l₂ заданы каноническими уравнениями

Обозначим = = (х₂—x₁,y₂—у₁,z₂—z₁), =(m₁,n₁,р),

= (m₂,n₂,р₂).

1) если прямые совпадают, то все три вектора , , коллинеарны.

2) если прямые параллельны и не совпадают, то вектора и коллинеарны, а вектор им не коллинеарен.

3) если пряже пересекаются, то никакие два из векторов , , не коллинеарны, и все три вектора компланарны

4) ecли прямые скрещиваются, то векторы , , некомпланарны.

Отметим, что условия параллельности и перпендикулярности прямых l₁ и l₂ равносильны условиям коллинеарности и ортогональности их направляющих векторов и .

— необходимое и достаточное условие параллельности двух прямых.

— необходимое и достаточное условие перпендикулярности двух прямых.

Если прямые l₁ и l₂ пересекаются, то величина угла φ между ними равно либо ( ^, ) либо (- ^, ). Следовательно,