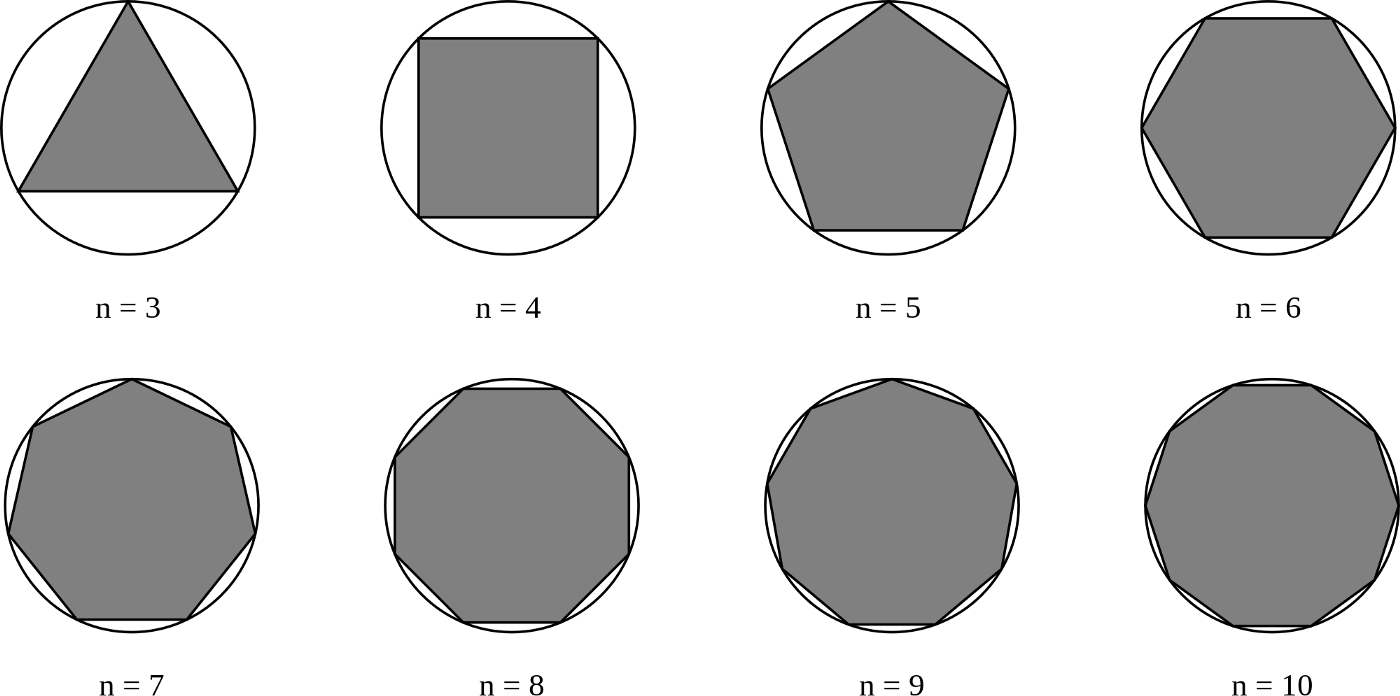
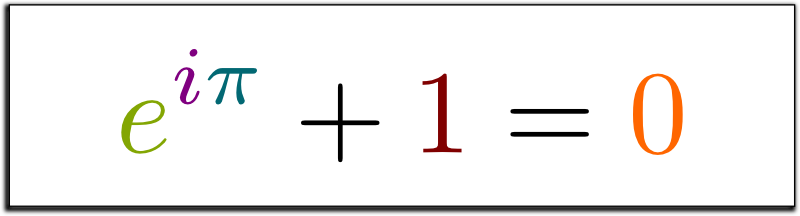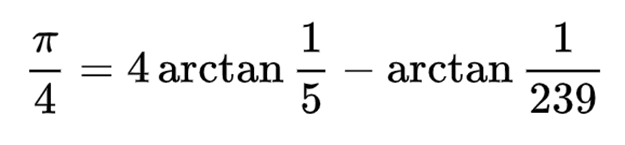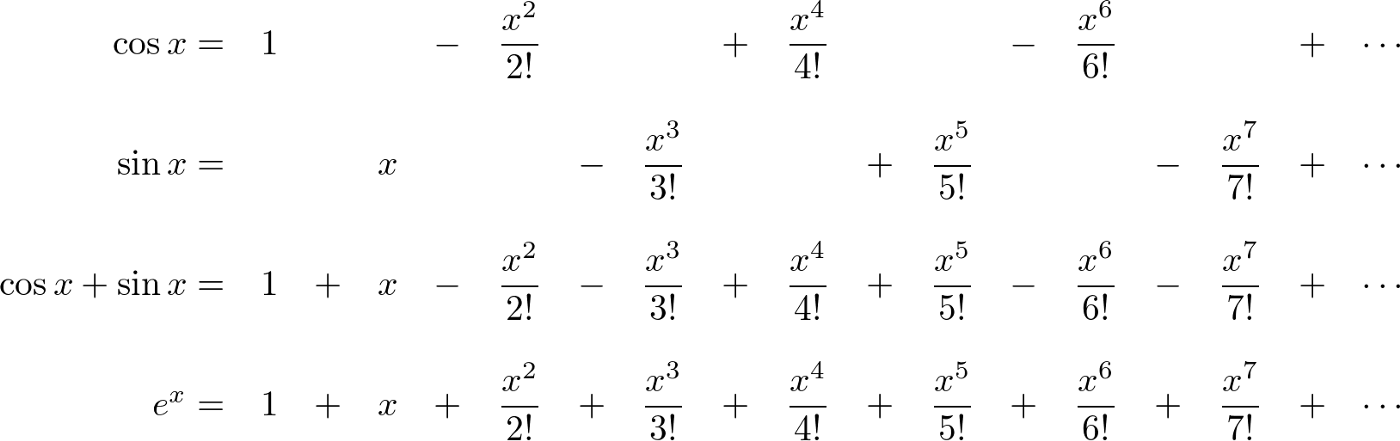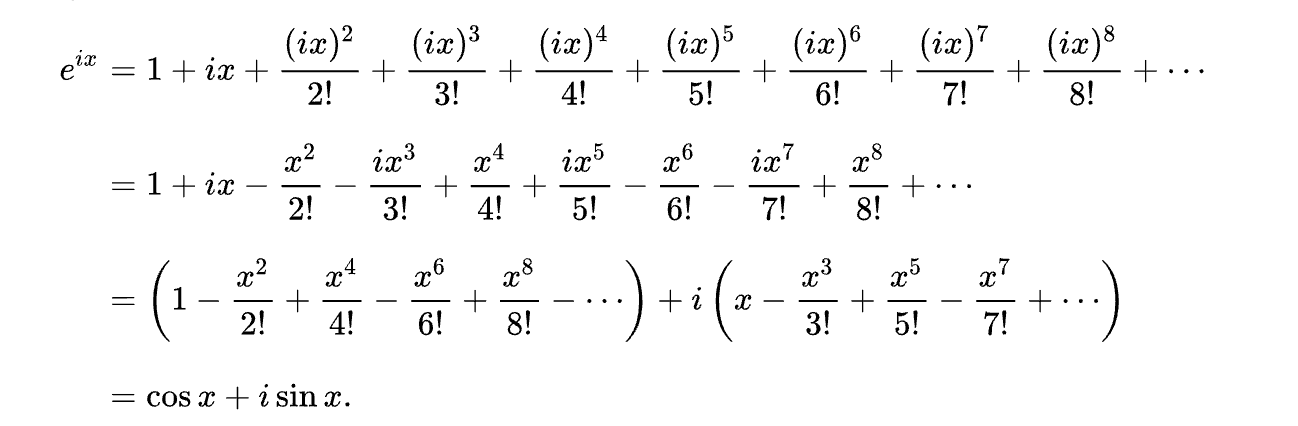T доказать что уравнение есть уравнение i
В дальнейшем будут использоваться следующие обозначения:
N = <0,1,2. >— множество натуральных чисел;
N * = <1,2. >— множество натуральных положительных чисел;
Z = <0,±1,±2. >— — множество целых чисел;
Q = < m /n | m Î Z, n Î N * > — множество рациональных чисел;
R — множество действительных (вещественных) чисел.
В начале представим некоторые определения и утверждения, необходимые для далнейшего изложения
Определение. Пусть a,b Î Z, b ≠ 0. Числа q Î Z и r Î <0,1. |b|-1> называются соответственно неполным частным и остатком от деления a на b, если выполнено равенство
| a = bq + r. | (1) |
При этом, если r = 0, то говорят, что a делится на b, или что b делит a, или что b является делителем a (обозначение a 
Доказывается, что для любых целых чисел a, b; b ≠ 0, существуют единственные целые числа q, r, r Î <0. |b| — 1> такие, что имеет место соотношение (1).
Определение. Наименьшим общим кратным ненулевых целых чисел a1, a2, . an называется наименьшее положительное число, которое делится на каждое из этих чисел (обозначение [a1, a2, . an]).
Определение. Наибольшим общим делителем целых чисел a1, a2, . an, из которых хотя бы одно отлично от нуля, называется наибольшее натуральное число, на которое делится каждое из этих чисел (обозначение (a1, a2, . an)).
Определение. Числа a,b Î Z называются взаимно простыми, если (a,b) = 1.
Определение. Пусть даны числа a,b Î Z, причем c ≠ 0. Говорят, что число a сравнимо с числом b по модулю c, (обозначение a ≡ b (mod c)), если c|a — b; в противном случае говорят, что число a не сравнимо с числом b по модулю c (обозначение a 
Определение. Натуральное положительное число, большее 1 и не имеющее натуральных положительных делителей, отличных от 1 и самого себя, называется постым. Остальные натуральные числа, большие 1, называются составными. Число 1 не является ни простым, ни составным.
Основная теорема арифметики.
Всякое натуральное число, большее 1, разлагается в произведение простых чисел (не обязательно различных), причем указанное разложение единственно с точностью до порядка следования множителей.
Малая теорема Ферма.
Пусть p — простое число. Тогда для любого целого числа a справедливо соотношение a p ≡ a(mod p).
О диофантовом анализе
При исследовании диофантовых уравнений обычно ставятся следующие вопросы:
- имеет ли уравнение целочисленные решения;
- конечно или бесконечно множество его целочисленных решений;
- решить уравнение на множестве целых чисел, т. е. найти все его целочисленные решения;
- решить уравнение на множестве целых положительных чисел;
- решить уравнение на множестве рациональных чисел.
Отметим, что проблема решения уравнений в целых числах решена до конца только для уравнений с одним неизвестным, для уравнений первой степени и для уравнений второй степени с двумя неизвестными. Для уравнений выше второй степени с двумя или более неизвестными достаточно трудной является даже задача существования целочисленных решений. Например, не известно, имеет ли уравнение x 3 + y 3 + z 3 = 30 хотя бы одно целочисленное решение. Более того, доказано, что в принципе не существует единого алгоритма, позволяющего за конечное число шагов решать в целых числах произвольные диафантовы уравнения.
Диофантовы уравнения с одним неизвестным
Рассмотрим уравнение
| a0 + a1x + . + anx n = 0, | (2) |
где aj Î Z ( j = 0. n), an ≠ 0.
Покажем, каким образом можно определить все рациональные корни уравнения (2) (этот метод позволяет, в частности, решать уравнения вида (2) в целых числах). Не нарушая общности рассуждений, можно считать, что a0 ≠ 0. Пусть r — рациональный корень уравнения (2), r = p /q, где p Î Z, q Î N * , (p,q) = 1. Умножая обе части равенства 
| p|a0q n и q|anp n . | (3) |
Так как (p,q) = 1, то (p,q n ) = 1, (q,p n ) = 1, поэтому из соотношений (3) следует, что p|a0, q|an. Поскольку рациональных чисел вида r = p /q, таких что (p,q) = 1, p|a0, q|an, конечное число, то за конечное число шагов можно выбрать те из них, которые являются решением уравнения (2). Как следует из приведенных выше рассуждений, других решений уравнение (2) иметь не может.
Задача 1. Решить в рациональных числах уравнение
| 2x 4 + 7x 3 — 12x 2 — 38x + 21 = 0. | (4) |
Решение. Свободный член уравнения имеет следующие делители ±1, ±3, ±7, ±21. Выпишем также положительные делители старшего коэффициента: 1, 2. Следовательно, для рационального корня уравнения (4) получаем следующие возможные значения:
Подстановкой в исходное уравнение убеждаемся, что из этого множества только числа -3 и 1 /2 являются его корнями.
Задача 2. Решить в целых числах уравнение
| x 8 + x 7 + x + 1 = 0. | (5) |
Решение. Делители свободного члена уравнения: ±1. Положительные делители старшего коэффициента: 1. Следовательно, все целые корни уравнения (5) находятся среди чисел <-1,1>. Подставляя x = ±1 в (5) заключаем, что только x = -1 является корнем этого уравнения.
Диофантовы уравнения первой степени
Перейдем теперь к решению в целых числах уравнений первой степени или так называемых линейных уравнений, т. е. уравнений вида
| a1x1 + a2x2 + . + anxn = b, | (6) |
где aj Î Z (j = 1,2. n), b Î Z.
Предположим, что не все числа aj (j = 1. n) равны нулю. Очевидно, для существования решения в целых числах уравнения (6) необходимо, чтобы (a1. an)|b. Покажем, что это условие является и достаточным.
Положив 
| a1 ¢ x1 + . + an ¢ xn = b ¢ , | (7) |
где (a1 ¢ , . an ¢ ) = 1. Пусть ai ¢ , aj ¢ — два ненулевых числа, таких, что |ai ¢ | ≠ |aj ¢ |. Для определенности предположим, что i ¢ | > |aj ¢ |. Разделив с остатком ai ¢ на aj ¢ , получим представление ai ¢ = aj ¢ q + r. Заменив ai ¢ на aj ¢ q + r в уравнении (7), приведем его к виду
| a1 ¢ x1 + . + rxi + . + aj ¢ (xj + qxi) + . + an ¢ xn = b ¢ . | (8) |
Перепишем уравнение (8) в виде
| a1 ¢ ¢ x1 + . + an ¢ ¢ xn ¢ ¢ = b ¢ , | (9) |
где
| ak ¢ ¢ = |
| , | xk ¢ ¢ = |
Очевидно, что решения уравнения (7) и (9). связаны между собой взаимно однозначным соответствием и, таким образом, решив уравнение (9), несложно найти все решения уравнения (7). С другой стороны отметим, что » k, i Î <1. n>, k ≠ i ak ¢ ¢ = ak ¢ , |ai ¢ ¢ | ¢ |. Следовательно, за конечное число шагов уравнение (7) приведется к виду
где числа Задача 3. Решить в целых числах уравнение 4x — 6y + 11z = 7. Решение. Разделив с остатком -6 на 4, получим -6 = 4(-2) + 2. Представим исходное уравнение в виде 4(x — 2y) + 2y + 11z = 7. После замены x ¢ = x — 2y это уравнение запишется следующим образом 4x ¢ + 2y + 11z = 7. Учитывая, что 11 = 2·5 + 1, преобразуем последнее уравнение: 4x ¢ + 2(y + 5z) + z = 7. Положив y ¢ = y + 5z, получим 4x ¢ + 2y ¢ + z = 7. Это уравнение имеет следующее решение: x ¢ , y ¢ — произвольные целые числа, z = 7 — 4x ¢ — 2y ¢ . Следовательно y = y ¢ — 5z = 20x ¢ + 11y ¢ — 35, x = x ¢ + 2y = 41x ¢ + 22y ¢ — 70. Таким образом, решение исходного уравнения имеет вид
где x ¢ , y ¢ — произвольные целые числа. Диофантовы уравнения высших степеней 1. Метод разложения на множители Задача 4. Решить в целых числах уравнение x + y = xy. Решение. Запишем уравнение в виде (x — 1)(y — 1) = 1. Произведение двух целых чисел может равняться 1 только в том случае, когда оба они равны 1. Т. е. исходное уравнение равносильно совокупности
с решениями (0,0) и (2,2). Задача 5. Доказать, что уравнение x 5 + 3x 4 y — 5x 3 y 2 — 15x 2 y 3 + 4xy 4 + 15y 5 = 33 неразрешимо в целых числах. Решение. Левая часть уравнения разлагается на множители следующим образом: (x — 2y)(x — y)(x + y)(x + 2y)(x + 3y). Если y ≠ 0, то в этом выражении все 5 множителей различны. С другой стороны, число 33 можно разделить максимум на 4 различных множителя. Следовательно, исходное уравнение не разрешимо в целых числах x, y при y ≠ 0. Случай y = 0 также невозможен, поскольку тогда исходное уравнение принимает вид x 5 = 33, Так как Задача 6. Доказать, что уравнение (x — y) 3 + (y — z) 3 + (z — x) 3 = 30 не имеет решений в целых числах. Решение. Разложив левую часть на множители, приведем уравнение к виду (x — y)(y — z)(z — x) = 10. Заметим, что (x — y) + (y — z) + (z — x) = 0. С другой стороны, делителями 10 являются числа ±1, ±2, ±5, ±10. Нетрудно проверить, что сумма любых трех чисел из этого множества, дающих в произведении 10, не будет равнятьса 0. Задача 7. Решить в целых числах уравнение y 3 — x 3 = 91. Решение. Перепишем исходное уравнение в виде (y — x)(y 2 + xy + x 2 ) = 91. Делителями числа 91 являются ±1, ±91. Так как y 2 + yx + x 2 ≥ y 2 — 2|y||x| + x 2 = (|y| — |x|) 2 ≥ 0, то исходное уравнение равносильно совокупности
Таким образом, целочисленными решениями исходного уравнения являются пары (-6,-5) и (5,6). Задача 8. Решить в натуральных числах уравнение y 2 — x(x + 1)(x + 2)(x + 3) = 1. Решение. Заметим, что
Следовательно, исходное уравнение равносильно уравнению y 2 = (x 2 + 3x + 1) 2 или y = x 2 + 3x + 1. Таким образом, множество всех решений имеет вид <(x , x 2 + 3x + 1) | x Î N>. 2. Использование четности Задача 9. Решить в простых числах уравнение
Решение. Рассмотрим два случая в зависимости от четности переменной x. a) Пусть x — нечетное число. Подстановка x = 2t + 1 приводит исходное уравнение к виду (2t + 1) 2 — 2y 2 = 1, или 2y 2 = 4t(t + 1). Следовательно, 2 | y 2 . Так как y — простое число, то y = 2. Отсюда b) Пусть x — четное число. Так как x — простое число, то x = 2. Следовательно, Следовательно, уравнение (11) имеет в классе простых чисел единственное решение (3;2). Задача 10. Решить в целых числах уравнение
Решение. Одно решение очевидно: x = y = z = 0. Покажем, что других решений в целых числах уравнение не имеет. Будем доказывать от противного. Пусть x, y, z — ненулевое решение исходного уравнения. Так как x 2 + y 2 + z 2 — четное число, то по крайней мере одно из чисел x, y, z — четное. Используя симметрию уравнения (12), предположим, что x = 2x1. — четное число. Тогда 4|y 2 + z 2 . Это может быть лишь в том случае, когда y и z — четные. Действительно, если одно из этих чисел четное, а другое нечетное, то число y 2 + z 2 — нечетное и 4 Повторением приведенных выше рассуждений доказывается, что 2|x1, 2|y1, 2|z1, следовательно, 2 2 |x, 2 2 |y, 2 2 |z. Рассуждая аналогично, получим, что для любого n Î N 2 n |x, 2 n |y, 2 n |z Противоречие. Следовательно, уравнение (12) имеет единственное решение (0,0,0). Задача 11. Доказать, что уравнение
в целых числах не имеет решений, не равных нулю одновременно. Решение. Предположим, что числа x, y, z, не равные одновременно нулю, являются решением исходного уравнения. Видно, что число x — четное. Подстановка x = 2x1 дает 4x1 3 + y 3 + 2z 3 — 6x1yz = 0. Отсюда следует, что число y — четное, y = 2y1. Учитывая это, получим 2x1 3 + 4y1 3 + z 3 — 6x1y1z = 0. Следовательно, z — также четное число. После подстановки z = 2z1 уравнение принимает вид x1 3 + 2y1 3 + 4z1 3 — 6x1y1z1 = 0. Рассуждая аналогично, доказывается, что для любого n Î N 2 n |x, 2 n |y, 2 n |z. Противоречие. 3. Доказательство неразрешимости уравнений с использованием сравнений Задача 12. Решить в целых числах уравнение
Решение. Пусть x, y — целые числа, удовлетворяющие уравнению (14 ). Тогда x 2 + 1 ≡ 0(mod 3). Рассмотрим случаи, соответствующие различным остаткам от деления x на 3. a) Пусть x ≡ 0(mod 3). Тогда x 2 + 1 ≡ 1(mod 3), значит x 2 + 1 b) Пусть x ≡ 1(mod 3). Тогда x 2 + 1 ≡ 2(mod 3), следовательно, x 2 + 1 c) Пусть x ≡ 2(mod 3). Тогда x 2 + 1 ≡ 5 ≡ 2 Задача 13. Решить в целых числах уравнение
Решение. Пусть (x, y, z) — целочисленное решение уравнения (15). Так как x — нечетное число, следовательно, x 2 = (2k + 1) 2 = 4k(k + 1) + 1 ≡ 1(mod 8). По модулю 4 исходное уравнение принимает вид 1 — 2y 2 ≡ 3(mod 4) или y 2 ≡ -1(mod 2). Следовательно, y — нечетное число, отсюда y 2 ≡ 1(mod 8). Поэтому, по модулю 8 исходное уравнение будет иметь вид 1 — 2 ≡ 3(mod 8) Û 4 ≡ 0(mod 8). Полученное противоречие доказывает неразрешимость исходное уравнение в целых числах. Задача 14. Доказать, что уравнение x 3 + x + 10y = 20004 неразрешимо в целых числах. Решение. По модулю 5 исходное уравнение принимает вид
Рассмотрев все возможные остатки от деления x на 5, убеждаемся, что сравнение (16) неразрешимо. Следовательно, исходное уравнение также неразрешимо в целых числах. 4. Другие методы решения диафантовых уравнений Задача 15. Доказать, что уравнение x 3 + y 3 + z 3 = 2 имеет бесконечно много решений в целых числах. Решение. Положим x = a + b, y = a — b. Тогда x 3 + y 3 = 2a 3 + 6ab 2 . С учетом последнего равенства исходное уравнение принимает вид 2a 3 + 6ab 2 + z 3 = 2. Положив a = 1, получим z 3 = -6b 2 . Положим теперь b = 6t 3 . Отсюда z = -6t 2 , x = 1 + 6t 3 , y = 1 — 6t 3 . Таким образом, получено бесконечное множество решений исходного уравнения, соответствующих целочисленным значениям параметра t Задача 16. Доказать, что уравнение
имеет бесконечно много решений в натуральных числах. Решение. Нетрудно заметить, что (3,2) — одно из решений исходного уравнения. С другой стороны из тождества (x 2 + 2y 2 ) 2 — 2(2xy) 2 = (x 2 — 2y 2 ) 2 следует, что если (x, y) — решение уравнения (17), то пара (x 2 + 2y 2 , 2xy) также является его решением. Используя этот факт, рекуррентно определим бесконечную последовательность (xn , yn) различных решений исходного уравнения: (x1 , y1) = (3,2) и xn+1 = xn 2 + 2yn 2 , yn+1 = 2xnyn, n Î N * . Задача 17. Решить в целых числах уравнение Решение. Заметим, что слагаемые в левой части уравнения имеют одинаковый знак, а поскольку их сумма положительна, то каждое слагаемое также положительно. Применяя неравенство Коши, получим Следовательно, xyz = 1. Отсюда получим, что решениями могут быть только тройки (1,1,1), (1,-1,-1), (-1,-1,1), (-1,1,-1). Проверкой убеждаемся, что каждая из них действительно является решением исходного уравнения. Задача 18. Доказать, что уравнение x(x + 1) = 4y(y + 1) неразрешимо в целых положительных числах. Решение. Нетрудно заметить, что исходное уравнение равносильно уравнению x 2 + x + 1 = (2y + 1) 2 . Следовательно, x 2 2 2 или x 2x 3 + xy — 7 = 0. Решение. Из условия следует, что x должен быть делителем числа 7. Т. е. возможные значения x находятся среди чисел <±1, ±7>. Перебрав эти возможности, получаем решение уравнения: (1,5), (-1,-9), (7,-97), (-7,-99). Задача 20. Доказать, что уравнение x 2 + 1 = py, где p — простое число вида 4k+3, неразрешимо в целых числах. Решение. Предположим, что исходное уравнение разрешимо в целых числах. Тогда x 2 + 1 ≡ 0(mod p). Но, согласно малой теореме Ферма, -1 ≡ (-1) 2k+1 ≡ (x 2 ) 2k+1 ≡ x p-1 ≡ 1(mod p). Полученное противоречие доказывает неразрешимость исходного уравнения в Z. Задача 21. Доказать, что уравнение x 2 — y 3 = 7 неразрешимо в целых положительных числах. Решение. Если y — четное число, то x 2 ≡ 3(mod 4), что невозможно. Поэтому предположим, что y — нечетное число: y = 2k + 1. Тогда x 2 + 1 = y 3 + 8 = (y + 2)((y + 1) 2 + 3) = (y + 2)(4(k + 1) 2 + 3), Итак, число x 2 + 1 имеет делитель вида 4n + 3. Следовательно, оно имеет и простой делитель вида 4n + 3 (действительно, если бы все простые делители числа 4(k + 1) 2 + 3 имели вид 4n + 1, то и само число, являясь их произведением, имело бы вид 4n + 1. Однако последнее невозможно в силу предыдущей задачи. Задача 22. Доказать, что уравнение Решение. Положим d = (x , y), x1 = x /d, y1 = y /d. Так как x 2 + xy + y 2 = x 2 y 2 , следовательно,
Отсюда получаем, что x1|y1, y1|x1. Учитывая, что (x1,y1) = 1, делаем вывод, что x1 = y1 = 1. Таким образом, уравнение (18) принимает вид d 2 = 3, Отсюда следует требуемое утверждение. Задача 23. Решить в целых числах уравнение x + y = x 2 — xy + y 2 . Решение. Положим t = x + y. Так как Учитывая соотношение x + y = (x + y) 2 — 3xy, рассмотрим случаи, соответствующие целочисленным значениям t из отрезка [0;4]. a) t = 0
b) t = 1
c) t = 2
d) t = 3
e) t = 4
Таким образом, целочисленными решениями исходного уравнения являются пары (0,0), (0,1), (1,0), (1,2), (2,1), (2,2). Задачи для самостоятельного решения
Самая красивая теорема математики: тождество ЭйлераПосмотрев лекцию профессора Робина Уилсона о тождестве Эйлера, я наконец смог понять, почему тождество Эйлера является самым красивым уравнением. Чтобы поделиться моим восхищением это темой и укрепить собственные знания, я изложу заметки, сделанные во время лекции. А здесь вы можете купить его прекрасную книгу. Что может быть более загадочным, чем взаимодействие мнимых чисел с вещественными, в результате дающее ничто? Такой вопрос задал читатель журнала Physics World в 2004 году, чтобы подчеркнуть красоту уравнения Эйлера «e в степени i, умноженного на пи равно минус единице». Рисунок 1.0: тождество Эйлера — e в степени i, умноженного на пи, плюс единица равно нулю. Ещё раньше, в 1988 году, математик Дэвид Уэллс, писавший статьи для американского математического журнала The Mathematical Intelligencer, составил список из 24 теорем математики и провёл опрос, попросив читателей своей статьи выбрать самую красивую теорему. И после того, как с большим отрывом в нём выиграло уравнение Эйлера, оно получило званием «самого красивого уравнения в математике». Рисунок 2.0: обложка журнала The Mathematical Intelligencer Рисунок 3.0: опрос Дэвида Уэллса из журнала Леонарда Эйлера называют самым продуктивным математиком за всю историю. Других выдающихся математиков вдохновляли его работы. Один из лучших физиков в мире, Ричард Фейнман, в своих знаменитых лекциях по физике назвал уравнение Эйлера «самой примечательной формулой в математике». Ещё один потрясающий математик, Майкл Атья, назвал эту формулу «…математическим аналогом фразы Гамлета — «быть или не быть» — очень короткой, очень сжатой, и в то же время очень глубокой». Существует множество интересных фактов об уравнении Эйлера. Например, оно встречалось в некоторых эпизодах «Симпсонов». Рисунок 4.0: в этой сцене уравнение Эйлера можно заметить на второй книге в самой правой стопке. Рисунок 5.0: в этой сцене уравнение Эйлера написано на футболке второстепенного персонажа. Также уравнение Эйлера стало ключевым пунктом в уголовном деле. В 2003 году аспирант Калифорнийского технологического института Билли Коттрелл писал краской на чужих спортивных автомобилях уравнение Эйлера. На суде он сказал: «Я знал теорему Эйлера с пяти лет, и её обязаны знать все«. Рисунок 6.0: марка, выпущенная в 1983 году в Германии в память о двухсотлетии со смерти Эйлера. Рисунок 7.0: марка, выпущенная Швейцарией в 1957 году в честь 250-й годовщины Эйлера. Почему уравнение Эйлера так важно?Вы имеете полное право задаться вопросом: почему Билли Коттрелл считал, что об уравнении Эйлера обязаны знать все? И был настолько в этом уверен, что начал писать его на чужих машинах? Ответ прост: Эйлер воспользовался тремя фундаментальными константами математики и применил математические операции умножения и возведения в степень, чтобы записать красивую формулу, дающую в результате ноль или минус один.
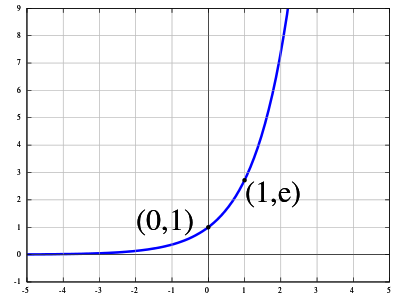
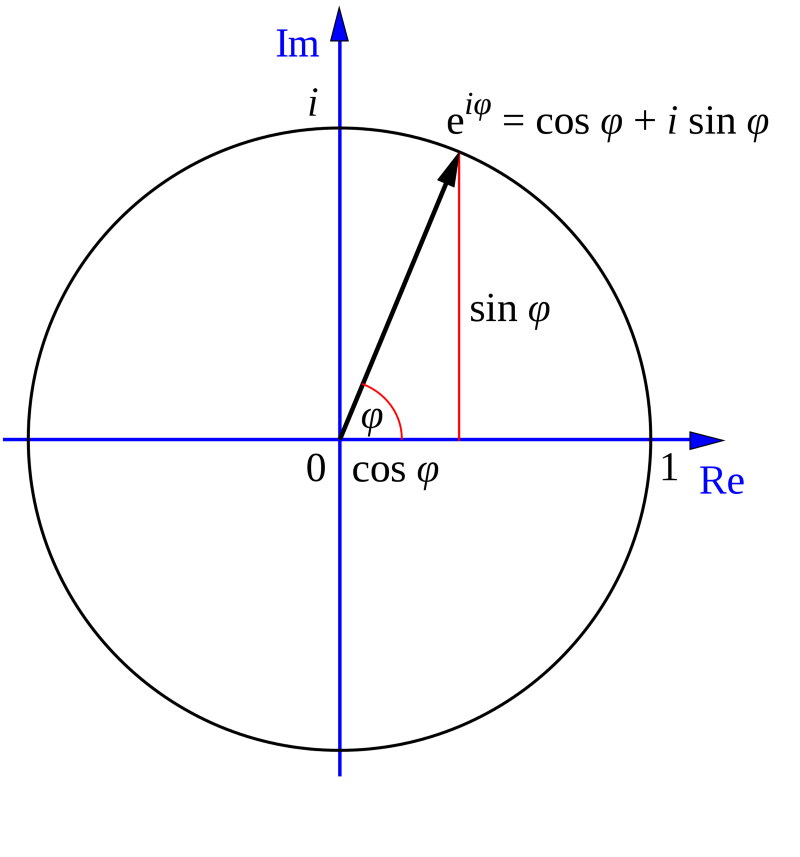
Впервые тождество Эйлера появилось в 1748 году в его книге Introductio in analysin infinitorum. Позже другие люди увидели, что эта формула связана с тригонометрическими функциями синуса и косинуса, и эта связь удивительна, ведь степенная функция стремится к бесконечности, а тригонометрические функции колеблются в интервале от — 1 до -1.
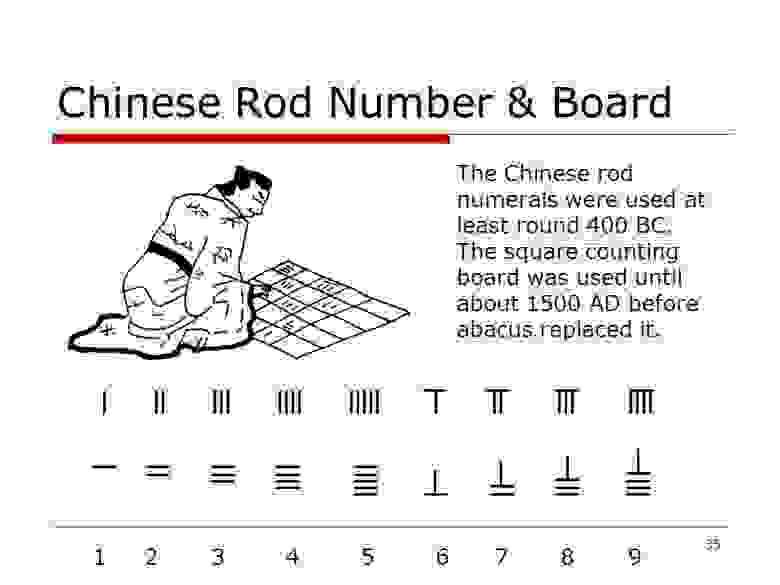
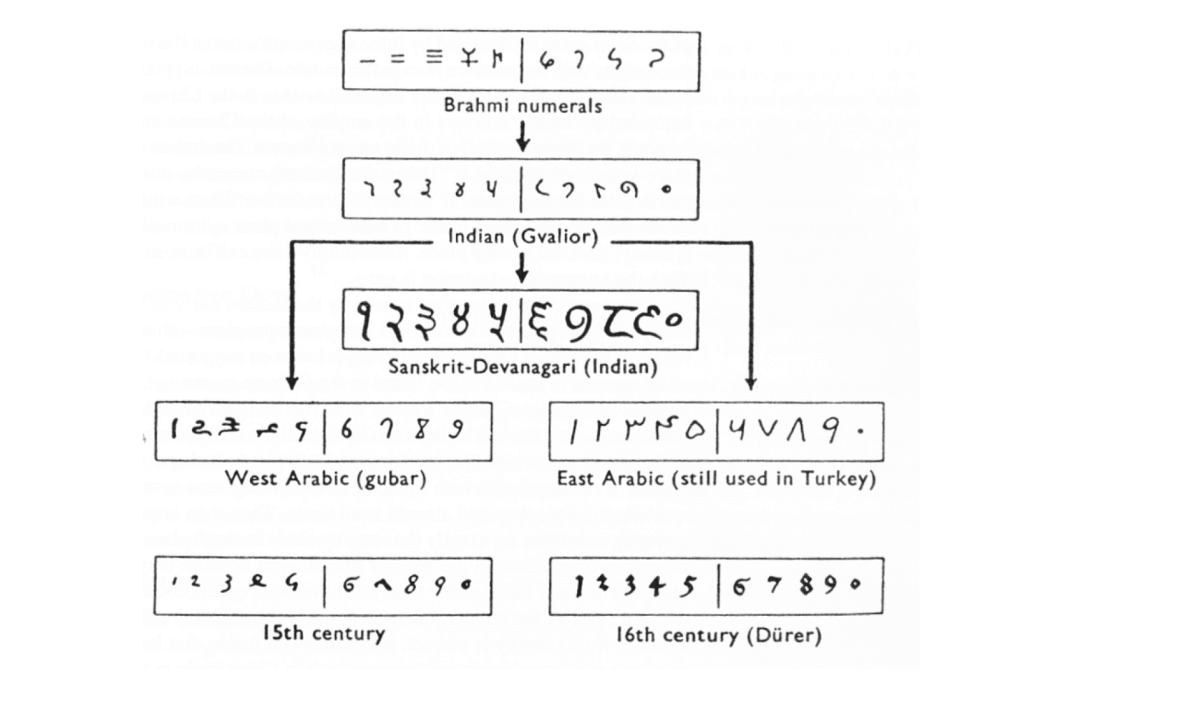
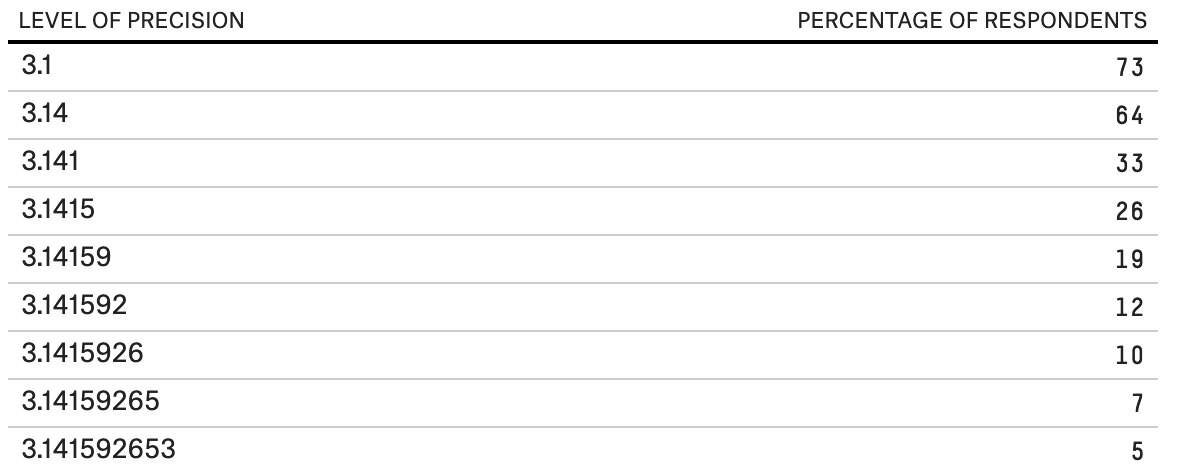
Рисунок 8.0: экспоненциальная функция y=e x . Рисунок 8.1: график тождества Эйлера. Рисунок 8.2: частоты, испускаемые LC-цепью. Показанные выше уравнения и графы могут показаться абстрактными, но они важны для квантовой физики и вычислений обработки изображений, и при этом зависят от тождества Эйлера. 1: число для счётаЧисло 1 (единица) является основой нашей системы исчисления. С неё мы начинаем счёт. Но как мы считаем? Чтобы считать, мы используем цифры 0–9 и систему разрядов, определяющую значение цифры. Например, число 323 означает 3 сотни, 2 десятка и 3 единицы. Здесь число 3 исполняет две разные роли, которые зависят от его расположения. 323 = (3*100) + (2*10) + (3*1) Существует и другая система исчисления, называемая двоичной. В этой системе вместо 10 используется основание 2. Она широко применяется в компьютерах и программировании. Например, в двоичной системе: 1001 = (2 3 ) + (0 2 ) + (0 1 ) + (2 0 ) = [9 в системе с основанием 10] Кто создал системы исчисления? Как первые люди считали предметы или животных? Как возникли наши системы исчисления? Как считали первые цивилизации? Мы точно знаем, что они не пользовались нашей разрядной системой. Например 4000 лет назад древние египтяне использовали систему исчисления с разными символами. Однако они комбинировали символы, создавая новый символ, обозначающий числа. Рисунок 11: показанные здесь иероглифы образуют число 4622; это одно из чисел, вырезанных на стене в храме в Карнаке (Египет). Рисунок 12: иероглифы — это изображения, обозначающие слова, а в данном случае — числа. В то же время, но в другом месте ещё один социум обнаружил способ подсчёта, но в нём тоже использовались символы. Кроме того, основанием их системы исчисления было 60, а не 10. Мы используем их метод счёта для определения времени; поэтому в минуте 60 секунд, а в часе 60 минут. Рисунок 13: вавилонские числа из шестидесятиричной системы счисления (с основанием 60). Тысячу лет спустя древние римляне изобрели римские числа. Для обозначения чисел они использовали буквы. Римская нотация не считается разрядной системой, потому что для многих значений нашей системы счисления в ней использовались разные буквы. Именно по этой причине для счёта они использовали абакус. Рисунок 14: романский абакус в шестнадцатеричной (с основанием 16) системе счисления Рисунок 15: таблица преобразования из арабских в римские числа Древние греки тоже не использовали разрядную систему счисления. Греческие математики обозначали числа буквами. У них были специальные буквы для чисел от 100 до 900. Многие люди в то время считали греческие числа запутанными. Рисунок 15: таблица букв древних греков. В то же самое время китайские математики начали использовать для расчётов небольшие бамбуковые палочки. Этот китайский способ счёта называют первой десятичной разрядной системой. Рисунок 16: китайский способ счёта с числами-палочками. Использовался как минимум с 400 года до нашей эры. Квадратная счётная доска использовалась примерно до 1500 года, когда её заменил абакус. Однако самая уникальная система счёта использовалась индейцами майя. Их система счисления имела основание 20. Для обозначения чисел от 1 до 19 они использовали точки и линии. Чем же отличалась их система счисления? Для каждого числа они использовали изображения голов и отдельный символ нуля 0. Рисунок 17: Система счисления майя с основанием 20, в которой числа обозначались головами Рисунок 18: ещё один способ записи чисел майя. 0: число для обозначения ничегоНекоторые цивилизации использовали пробелы, чтобы, например, отличать число 101 от 11. Спустя какое-то время начало появляться особое число — ноль. К примеру, в пещере в индийском городе Гвалиор археологи обнаружили на стене число 270, в котором был ноль. Самое первое зафиксированное использование нуля можно увидеть в Бодлианской библиотеке. Рисунок 19: вырезанный на стене храма в Гвалиоре круг обозначает ноль. Ему примерно 1500 лет. Рисунок 20: чёрные точки в манускрипте Бакхшали обозначают нули; это самый старый письменный пример использования числа, ему примерно 1800 лет. Примерно 1400 лет назад были записаны правила вычислений с нулём. Например, при сложении отрицательного числа и нуля получается то же отрицательное число. Деление на нуль не допускается, потому что если разделить на ноль, то мы получим число, которое может быть равно любому нужному нам числу, что должно быть запрещено. Вскоре после этого многими людьми были опубликованы книги по арифметике, распространяющие использование индо-арабской записи чисел. Ниже показана эволюция индо-арабских чисел. В большинстве стран используется индо-арабская система чисел, но арабские страны до сих пор пользуются арабскими числами. Рисунок 21: на этой схеме показана эволюция чисел, происходящих от чисел брахми и заканчивающаяся числами, которыми мы используем и сегодня. Рисунок 22: классическая гравюра «Арифметика» из Margarita Philosophica Грегора Рейша, на которой изображено соревнование между Боэцием, улыбающимся после открытия индо-арабских чисел и письменных вычислений, и нахмуренным Пифагором, до сих пор пытающимся пользоваться счётной доской. Пи (π): самое известное иррациональное числоПи — самое популярное из известных нам иррациональных чисел. Пи можно найти двумя способами: вычислив соотношение длины окружности к её диаметру, или соотношение площади круга к квадрату его радиуса. Евклид доказал, что эти соотношения постоянны для всех окружностей, даже для луны, пенни, шины и т.д. π = окружность / диаметр ИЛИ π = площадь круга / радиус²Рисунок 22: анимированная связь между окружностью и диаметром в отношении пи. Так как иррациональные числа наподобие пи бесконечны и не имеют повторений, мы никогда не закончим записывать пи. Оно продолжается вечно. Есть люди, запомнившие множество десятичных разрядов пи (нынешний рекорд — 70 000 цифр! Источник: «Книга рекордов Гиннесса» ). Рисунок 23: данные опроса 941 респондентов для определения процента людей, способных запомнить знаки пи после запятой. Рисунок 24: На стене станции метро Karlsplatz в Вене записаны сотни разрядов пи. На данный момент компьютеры смогли вычислить всего 2,7 триллиона разрядов пи. Может казаться, что это много, но на самом деле этот путь бесконечен. Как я сказал выше, число пи нашёл Евклид. Но как поступали люди до Евклида, когда им нужно было найти площадь круга? Историки обнаружили вавилонскую глиняную табличку, в которой было записано отношение периметра шестиугольника к диаметру описанной вокруг него окружности. После вычислений полученное число оказалось равным 3.125. Это очень близко к пи. Рисунок 24: вавилонская глиняная табличка с отношением периметра шестиугольника к длине описанной окружности. Древние египтяне тоже близко подобрались к значению пи. Историки обнаружили документ, показывающий, как древние египтяне нашли число пи. Когда историки перевели документ, то нашли такую задачу:
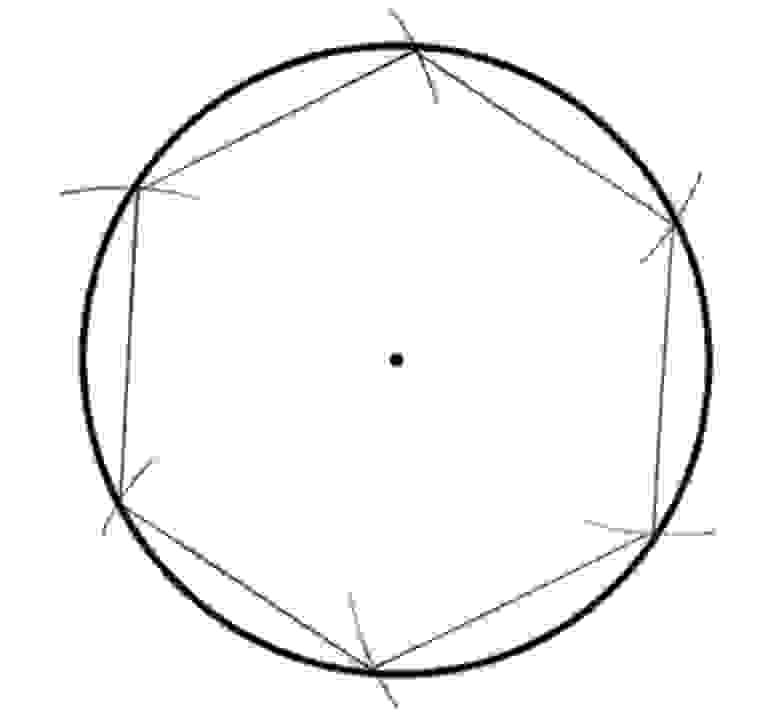
Вычесть 1/9 диаметра, а именно 1. Остаток равен 8. Умножить его на 8, что даёт нам 64. Следовательно, площадь будет равна 64 setjat (единица измерения площади). Другими словами, диаметр равен 2r, а 1/9 радиуса равно (1/9 • 2r). Тогда если мы вычтем это из исходного диаметра, то получим 2r — (1/9 • 2r) = 8/9(2r). Тогда площадь круга равна 256/81 r². То есть пи равно почти 3,16. Они обнаружили это значение пи примерно 4000 лет назад. Однако греческие математики нашли для вычисления пи способ получше. Например, Архимед предпочитал работать с периметрами. Он начал рисовать окружности, описывающие многоугольники разного размера. Когда он чертил шестиугольник, то рисовал окружность с диаметром 1. Затем он видел что каждая сторона шестиугольника равна 1/2, а периметр шестиугольника равен 1/2 x 6 = 3. Затем он увеличивал количество сторон многоугольника, пока он не становился похожим на круг. Работая со 96-сторонним многоугольником и применив тот же способ, он получил 2 десятичных разряда пи после запятой: 3 и 10/71 = 3,14084. Спустя много лет китайский математик Лю Ху использовал 3072-сторонний многоугольник и получил число 3,14159 (5 верных десятичных разрядов числа пи после запятой). После этого ещё один китайский математик Цзу Чунчжи провёл ещё более впечатляющую работу. Он работал со 24000-сторонним многоугольником и получил 3,1415926 — семь верных десятичных разрядов пи после запятой. Спустя тысячу лет немецкий математик Людольф Цейлен работал со 2 62 -сторонним многоугольником и получил 35 десятичных разрядов пи. Это число, названное Людольфовым, было высечено на его могильном камне. В 1706 году англичанин Джон Мэчин, долгое время работавший профессором астрономии, использовал формулу сложения, чтобы доказать, что пи равно Не беспокоясь о том, как откуда взялась эта формула, Мэчин начал постоянно ею пользоваться, а затем записал показанный ниже ряд. Это был самый большой на то время шаг в количестве разрядов пи. Однако первое упоминание пи появилось в 1706 году. Преподаватель математики Уильям Джонс написал книгу и впервые предложил пи для измерения окружностей. Так пи впервые появилась в книгах! В 1873 году Уильям Шэнкс воспользовался формулой Джона Мэчина и получил 707 десятичных разрядов пи. Эти цифры написаны в комнате пи парижского Дворца открытий. Однако позже математики выяснили, что верными являются только 527 разрядов. Рисунок 31: комната пи С другой стороны, более интересный способ нахождения пи обнаружил Буффон. Его эксперимент основывался на случайном разбрасывании иголок для оценки пи. Он нарисовал на доске несколько параллельных линий на расстоянии D и взял иголки длиной L. Затем он случайным образом начал бросать иголки на доску и записывал долю иголок, пересекавших линию. А после этого другой математик по имени Ладзарини подбросил иголку 3408 раз и получил шесть десятичных разрядов пи с соотношением 355/113. Однако если бы одна иголка не пересекла линию, он получил бы только 2 разряда пи. Рисунок 32.1: бросание 1000 иголок для оценки приблизительного значения пи e: история экспоненциального ростаe — это ещё одно знаменитое иррациональное число. Дробная часть e тоже бесконечна, как и у пи. Мы используем число e для вычисления степенного (экспоненциального) роста. Другими словами, мы используем e, когда видим очень быстрый рост или уменьшение. Один из величайших, а возможно и лучший математик Леонард Эйлер открыл число e в 1736 году и впервые упомянул это особое число в своей книге Mechanica. Чтобы разобраться в экспоненциальном росте, мы можем использовать историю об изобретателе шахмат. Когда он придумал эту игру, то показал её властителю Севера. Царю понравилась игра и он пообещал, что отдаст автору любую награду. Тогда изобретатель попросил нечто очень простое: 2 0 зерна на первую клетку шахматной доски, 2 1 зерна на вторую клетку доски, 2 2 зерна — на третью, и так далее. Каждый раз количество зерна удваивалось. Царь Севера подумал, что просьбу будет выполнить легко, но он ошибался, потому то на последнюю клетку нужно было бы положить 2 63 зёрен, что равно 9 223 372 036 854 775 808. Это и есть экспоненциальный рост. Он начался с 1, постоянно удваивался, и через 64 шага вырос в огромное число! Если бы изобретатель шахмат выбрал линейное уравнение, например 2n, то получил бы 2, 4, 6, 8, … 128… Следовательно, в дальней перспективе экспоненциальный рост часто намного превышает полиномиальный.
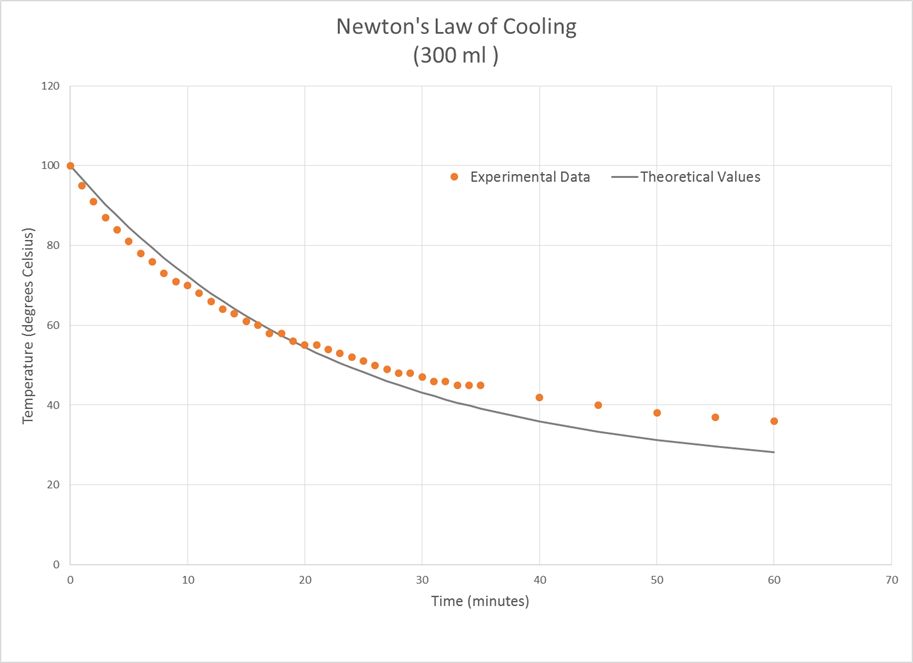
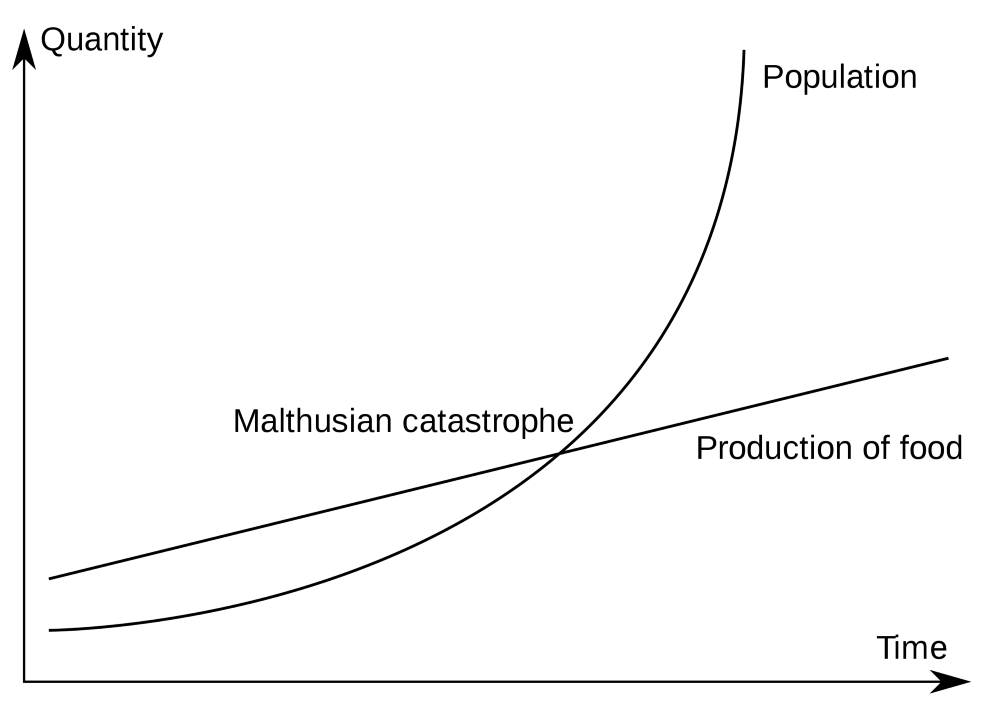
Число e открыл Эйлер. Однако Якоб Бернулли тоже работал с числом e, когда вычислял сложный процент, чтобы заработать больше денег. Если вложить 100 долларов под 10% дохода, то как будет расти эта сумма? Во-первых, это зависит от того, как часто банк рассчитывает проценты. Например, если он рассчитывает один раз, то мы получим в конце года 110 долларов. Если мы передумаем и будем брать проценты каждые 6 месяцев, то в этом случае мы получим больше 110 долларов. Дело в ттом, что процент, полученный за первые 6 месяцев, тоже получит свой процент. Общая сумма будет равна 110,25 долларов. Можно догадаться, что мы можем получить больше денег, если будем забирать деньги каждый квартал года. А если мы будем делать временной интервал всё короче, то окончательные суммы будут продолжать расти. Такой бесконечный сложный процент сделает нас богатыми! Однако наш общий доход стремится к ограниченному значению, связанному с e. Бернулли не называл число 2,71828 именем e. Когда Эйлер работал с 2,71828, он возвёл экспоненциальную функцию e в степень x. Свои открытия он изложил в книге The Analysis of Infinite. В 1798 году Томас Мальтус использовал экспоненциальную функцию в своём эссе, посвящённом пищевому дефициту будущего. Он создал линейный график, показывающий производство пищи и экспоненциальный график, показывающий население мира. Мальтус сделал вывод, что в дальней перспективе экспоненциальный рост победит, и мир ждёт серьёзный дефицит пищи. Это явление назвали «мальтузианской катастрофой». Ньютон тоже использовал эту модель, чтобы показать, как охлаждается чашка чая. Рисунок 35: закон Ньютона-Рихмана Рисунок 36: мальтузианская катастрофа Мнимость числа: i, квадратный корень -1Долгое время для решения своих задач математикам было достаточно обычных чисел. Однако в какой-то момент для дальнейшего развития им потребовалось открыть нечто новое и загадочное. Например, итальянский математик Кардано пытался разделить число 10 на 2 части, произведение которых было бы равно 40. Чтобы решить эту задачу, он записал уравнение: x (10-x) = 40. Когда он решил это квадратное уравнение, то получил два решения: 5 плюс √-15 и 5 минус √-15, что в то время не имело никакого смысла. Этот результат был бессмысленным, потому что по определению квадратного корня ему нужно было найти число, квадрат которого был бы отрицательным. Однако и положительное, и отрицательное числа в квадрате имеют положительное значение. Как бы то ни было, он нашёл своё уникальное число. Однако первым математиком, назвавшим √-1 (квадратный корень из минус единицы) мнимым числом i, был Эйлер. Лейбниц дал такой комментарий о мнимом числе √-1:
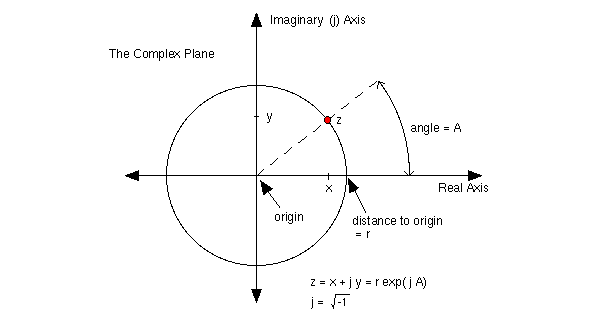
Мы можем складывать, вычитать, умножать и делить мнимые числа. Сложение, вычитание и умножение просты, а деление немного сложнее. Вещественные и мнимые части складываются по отдельности. В случае умножения i 2 будет равно -1. После Эйлера математик Каспар Вессель представил мнимые числа геометрически с создал комплексную плоскость. Сегодня мы представляем каждое комплексное число a + bi как точку с координатами (a,b). Рисунки 37 и 38: комплексные числа В викторианскую эпоху многие относились к мнимым числам с подозрением. Однако ирландский математик и астроном Уильям Роуэн Гамильтон покончил с этими сомнениями, определив комплексные числа применительно к кватернионам. Самое красивое уравнение: тождество ЭйлераТождество Эйлера связывает экспоненциальную функцию с функциями синуса и косинуса, значения которых колеблются от минус единицы до единицы. Чтобы найти связь с тригонометрическими функциями, мы можем представить их в виде бесконечного ряда, истинного для всех значений Рисунок 40: тождество Эйлера Эйлер никогда не записывал это тождество в явном виде, и мы не знаем, кто впервые записал его. Тем не менее, мы связываем его с именем Эйлера в знак почтения перед этим великим первопроходцем математики. Общее уравнение прямой: описание, примеры, решение задачДанная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач. Общее уравнение прямой: основные сведенияПусть на плоскости задана прямоугольная система координат O x y . Любое уравнение первой степени, имеющее вид A x + B y + C = 0 , где А , В , С – некоторые действительные числа ( А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид A x + B y + C = 0 при некотором наборе значений А , В , С . указанная теорема состоит из двух пунктов, докажем каждый из них.
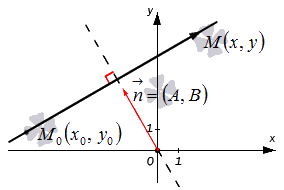
Пусть существует некоторая точка М 0 ( x 0 , y 0 ) , координаты которой отвечают уравнению A x + B y + C = 0 . Таким образом: A x 0 + B y 0 + C = 0 . Вычтем из левой и правой частей уравнений A x + B y + C = 0 левую и правую части уравнения A x 0 + B y 0 + C = 0 , получим новое уравнение, имеющее вид A ( x — x 0 ) + B ( y — y 0 ) = 0 . Оно эквивалентно A x + B y + C = 0 . Полученное уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 является необходимым и достаточным условием перпендикулярности векторов n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) . Таким образом, множество точек M ( x , y ) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n → = ( A , B ) . Можем предположить, что это не так, но тогда бы векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) не являлись бы перпендикулярными, и равенство A ( x — x 0 ) + B ( y — y 0 ) = 0 не было бы верным. Следовательно, уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение A x + B y + C = 0 определяет ту же прямую. Так мы доказали первую часть теоремы.
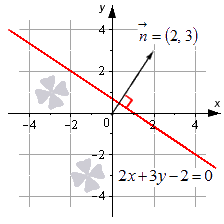
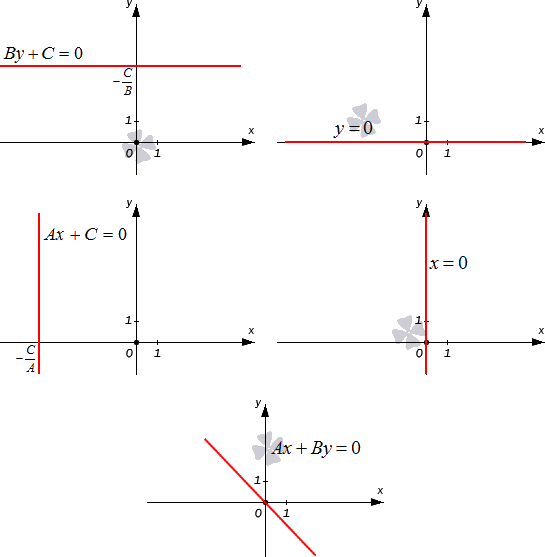
Зададим в прямоугольной системе координат на плоскости прямую a ; точку M 0 ( x 0 , y 0 ) , через которую проходит эта прямая, а также нормальный вектор этой прямой n → = ( A , B ) . Пусть также существует некоторая точка M ( x , y ) – плавающая точка прямой. В таком случае, векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) являются перпендикулярными друг другу, и их скалярное произведение есть нуль: n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) = 0 Перепишем уравнение A x + B y — A x 0 — B y 0 = 0 , определим C : C = — A x 0 — B y 0 и в конечном результате получим уравнение A x + B y + C = 0 . Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом. Уравнение, имеющее вид A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат O x y . Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая. Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой A x + B y + C = 0 . Рассмотрим конкретный пример общего уравнения прямой. Пусть задано уравнение 2 x + 3 y — 2 = 0 , которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n → = ( 2 , 3 ) . Изобразим заданную прямую линию на чертеже. Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2 x + 3 y — 2 = 0 , поскольку координаты всех точек заданной прямой отвечают этому уравнению. Мы можем получить уравнение λ · A x + λ · B y + λ · C = 0 , умножив обе части общего уравнения прямой на число λ , не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости. Неполное уравнение общей прямойПолное общее уравнение прямой – такое общее уравнение прямой A x + B y + C = 0 , в котором числа А , В , С отличны от нуля. В ином случае уравнение является неполным. Разберем все вариации неполного общего уравнения прямой.
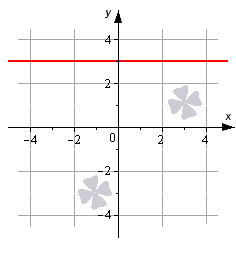
Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой. Известно, что заданная прямая параллельна оси ординат и проходит через точку 2 7 , — 11 . Необходимо записать общее уравнение заданной прямой. Решение Прямая, параллельная оси ординат, задается уравнением вида A x + C = 0 , в котором А ≠ 0 . Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения A x + C = 0 , т.е. верно равенство: Из него возможно определить C , если придать A какое-то ненулевое значение, к примеру, A = 7 . В таком случае получим: 7 · 2 7 + C = 0 ⇔ C = — 2 . Нам известны оба коэффициента A и C , подставим их в уравнение A x + C = 0 и получим требуемое уравнение прямой: 7 x — 2 = 0 Ответ: 7 x — 2 = 0 На чертеже изображена прямая, необходимо записать ее уравнение. Решение Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси O x и проходит через точку ( 0 , 3 ) . Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение B y + С = 0 . Найдем значения B и C . Координаты точки ( 0 , 3 ) , поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой B y + С = 0 , тогда справедливым является равенство: В · 3 + С = 0 . Зададим для В какое-то значение, отличное от нуля. Допустим, В = 1 , в таком случае из равенства В · 3 + С = 0 можем найти С : С = — 3 . Используем известные значения В и С , получаем требуемое уравнение прямой: y — 3 = 0 . Ответ: y — 3 = 0 . Общее уравнение прямой, проходящей через заданную точку плоскостиПусть заданная прямая проходит через точку М 0 ( x 0 , y 0 ) , тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: A x 0 + B y 0 + C = 0 . Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A ( x — x 0 ) + B ( y — y 0 ) + C = 0 , это уравнение эквивалентно исходному общему, проходит через точку М 0 ( x 0 , y 0 ) и имеет нормальный вектор n → = ( A , B ) . Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой. Даны точка М 0 ( — 3 , 4 ) , через которую проходит прямая, и нормальный вектор этой прямой n → = ( 1 , — 2 ) . Необходимо записать уравнение заданной прямой. Решение Исходные условия позволяют нам получить необходимые данные для составления уравнения: А = 1 , В = — 2 , x 0 = — 3 , y 0 = 4 . Тогда: A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 1 · ( x — ( — 3 ) ) — 2 · y ( y — 4 ) = 0 ⇔ ⇔ x — 2 y + 22 = 0 Задачу можно было решить иначе. Общее уравнение прямой имеет вид A x + B y + C = 0 . Заданный нормальный вектор позволяет получить значения коэффициентов A и B , тогда: A x + B y + C = 0 ⇔ 1 · x — 2 · y + C = 0 ⇔ x — 2 · y + C = 0 Теперь найдем значение С, используя заданную условием задачи точку М 0 ( — 3 , 4 ) , через которую проходит прямая. Координаты этой точки отвечают уравнению x — 2 · y + C = 0 , т.е. — 3 — 2 · 4 + С = 0 . Отсюда С = 11 . Требуемое уравнение прямой принимает вид: x — 2 · y + 11 = 0 . Ответ: x — 2 · y + 11 = 0 . Задана прямая 2 3 x — y — 1 2 = 0 и точка М 0 , лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна — 3 . Необходимо определить ординату заданной точки. Решение Зададим обозначение координат точки М 0 как x 0 и y 0 . В исходных данных указано, что x 0 = — 3 . Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство: 2 3 x 0 — y 0 — 1 2 = 0 Определяем y 0 : 2 3 · ( — 3 ) — y 0 — 1 2 = 0 ⇔ — 5 2 — y 0 = 0 ⇔ y 0 = — 5 2 Ответ: — 5 2 Переход от общего уравнения прямой к прочим видам уравнений прямой и обратноКак мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида. Для начала рассмотрим переход от общего уравнения вида A x + B y + C = 0 к каноническому уравнению x — x 1 a x = y — y 1 a y . Если А ≠ 0 , тогда переносим слагаемое B y в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: A x + C A = — B y . Это равенство возможно записать как пропорцию: x + C A — B = y A . В случае, если В ≠ 0 , оставляем в левой части общегь уравнения только слагаемое A x , прочие переносим в правую часть, получаем: A x = — B y — C . Выносим – В за скобки, тогда: A x = — B y + C B . Перепишем равенство в виде пропорции: x — B = y + C B A . Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому. Задано общее уравнение прямой 3 y — 4 = 0 . Необходимо преобразовать его в каноническое уравнение. Решение Запишем исходное уравнение как 3 y — 4 = 0 . Далее действуем по алгоритму: в левой части остаётся слагаемое 0 x ; а в правой части выносим — 3 за скобки; получаем: 0 x = — 3 y — 4 3 . Запишем полученное равенство как пропорцию: x — 3 = y — 4 3 0 . Так, мы получили уравнение канонического вида. Ответ: x — 3 = y — 4 3 0 . Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям. Прямая задана уравнением 2 x — 5 y — 1 = 0 . Запишите параметрические уравнения этой прямой. Решение Осуществим переход от общего уравнения к каноническому: 2 x — 5 y — 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2 Теперь примем обе части полученного канонического уравнения равными λ , тогда: x 5 = λ y + 1 5 2 = λ ⇔ x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R Ответ: x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y = k · x + b , но только тогда, когда В ≠ 0 . Для перехода в левой части оставляем слагаемое B y , остальные переносятся в правую. Получим: B y = — A x — C . Разделим обе части полученного равенство на B , отличное от нуля: y = — A B x — C B . Задано общее уравнение прямой: 2 x + 7 y = 0 . Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом. Решение Произведем нужные действия по алгоритму: 2 x + 7 y = 0 ⇔ 7 y — 2 x ⇔ y = — 2 7 x Ответ: y = — 2 7 x . Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида x a + y b = 1 . Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на – С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y : A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1 Необходимо преобразовать общее уравнение прямой x — 7 y + 1 2 = 0 в уравнение прямой в отрезках. Решение Перенесем 1 2 в правую часть: x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 . Разделим на -1/2 обе части равенства: x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 . Преобразуем далее в необходимый вид: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 . Ответ: x — 1 2 + y 1 14 = 1 . В общем, несложно производится и обратный переход: от прочих видов уравнения к общему. Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства: x a + y b ⇔ 1 a x + 1 b y — 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y — k x — b = 0 ⇔ A x + B y + C = 0 Каноническое уравнение преобразуется к общему по следующей схеме: x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x ( y — y 1 ) ⇔ ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0 Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему: x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ A x + B y + C = 0 Заданы параметрические уравнения прямой x = — 1 + 2 · λ y = 4 . Необходимо записать общее уравнение этой прямой. Решение Осуществим переход от параметрических уравнений к каноническому: x = — 1 + 2 · λ y = 4 ⇔ x = — 1 + 2 · λ y = 4 + 0 · λ ⇔ λ = x + 1 2 λ = y — 4 0 ⇔ x + 1 2 = y — 4 0 Перейдем от канонического к общему: x + 1 2 = y — 4 0 ⇔ 0 · ( x + 1 ) = 2 ( y — 4 ) ⇔ y — 4 = 0 Ответ: y — 4 = 0 Задано уравнение прямой в отрезках x 3 + y 1 2 = 1 . Необходимо осуществить переход к общему виду уравнения. Решение: Просто перепишем уравнение в необходимом виде: x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y — 1 = 0 Ответ: 1 3 x + 2 y — 1 = 0 . Составление общего уравнения прямойВыше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A ( x — x 0 ) + B ( y — y 0 ) = 0 . Там же мы разобрали соответствующий пример. Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора. Задана прямая, параллельная прямой 2 x — 3 y + 3 3 = 0 . Также известна точка M 0 ( 4 , 1 ) , через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой. Решение Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n → = ( 2 , — 3 ) : 2 x — 3 y + 3 3 = 0 . Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой: A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 2 ( x — 4 ) — 3 ( y — 1 ) = 0 ⇔ 2 x — 3 y — 5 = 0 Ответ: 2 x — 3 y — 5 = 0 . Заданная прямая проходит через начало координат перпендикулярно прямой x — 2 3 = y + 4 5 . Необходимо составить общее уравнение заданной прямой. Решение Нормальный вектором заданной прямой будет направляющий вектор прямой x — 2 3 = y + 4 5 . Тогда n → = ( 3 , 5 ) . Прямая проходит через начало координат, т.е. через точку О ( 0 , 0 ) . Составим общее уравнение заданной прямой: A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 3 ( x — 0 ) + 5 ( y — 0 ) = 0 ⇔ 3 x + 5 y = 0 источники: http://habr.com/ru/post/454136/ http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/obschee-uravnenie-prjamoj/ |
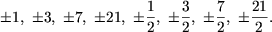

 (i = 1. n), которые не равны нулю, равны между собой по абсолютной величине. Из соотношения
(i = 1. n), которые не равны нулю, равны между собой по абсолютной величине. Из соотношения  следует, что числа
следует, что числа  . Тогда уравнение (10) имеет следующее решение:
. Тогда уравнение (10) имеет следующее решение:  где t2, t3, . tn — произвольные целые числа. Отсюда, учитывая проведенные замены, получается и решение уравнения (7). Отметим, что при получении решения уравнения (10) использовался лишь факт, что
где t2, t3, . tn — произвольные целые числа. Отсюда, учитывая проведенные замены, получается и решение уравнения (7). Отметим, что при получении решения уравнения (10) использовался лишь факт, что 
 исходное уравнение не имеет целочисленных решений и в случае y = 0.
исходное уравнение не имеет целочисленных решений и в случае y = 0.
 т. е. уравнение неразрешимо в простых числах.
т. е. уравнение неразрешимо в простых числах. y 2 + z 2 . Если же оба эти числа (z и y) нечетные, то y 2 + z 2 = (2u + 1) 2 + (2v + 1) 2 = 4(u 2 + v 2 + u + v) + 2 ≡ 2(mod 4),
y 2 + z 2 . Если же оба эти числа (z и y) нечетные, то y 2 + z 2 = (2u + 1) 2 + (2v + 1) 2 = 4(u 2 + v 2 + u + v) + 2 ≡ 2(mod 4),

 не имеет решений в целых положительных числах.
не имеет решений в целых положительных числах. то должно выполнятся неравинство
то должно выполнятся неравинство  откуда t Î [0;4].
откуда t Î [0;4]. Указание. Применить неравинство Коши.
Указание. Применить неравинство Коши.  где параметр p — простое число больше 2.
где параметр p — простое число больше 2.