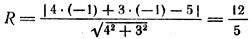T находить радиус окружности заданной уравнением

Нахождение центра и радиуса окружности по общему уравнению окружности

Этот калькулятор проверяет, является ли введенное уравнение общим уравнением окружности, и вычисляет координаты центра и радиуса окружности, если это возможно. Описание способа решения подобных задач находится под калькулятором

Нахождение центра и радиуса окружности по общему уравнению окружности

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Калькулятор выше можно применять для решения задач на уравнение окружности. Чаще всего вы имеете дело с уравнением окружности, выраженном в так называемом стандартном виде

Из этого уравнения достаточно легко найти центр окружности — это будет точка с координатами (a,b), и радиус окружности — это будет квадратный корень из правой части уравнения.

Однако, если возвести в квадрат выражения в скобках и перенести правую часть налево, то уравнение станет выглядеть примерно так:

Это — уравнение окружности в общем виде. Здесь радиус и центр окружности уже не выделены явно, и в задачах обычно просят их найти именно по общему виду уравнения окружности.

Способ решения такого рода задач следующий:

Перегруппируем слагаемые уравнения

Как видим, выражение в конце это уравнение окружности в стандартном виде, из которого уже легко получить и координаты центра окружности и ее радиус. Если же справа получилось отрицательное число — значит заданное вначале уравнение не является уравнением окружности (бывают задачи и на такую проверку). Калькулятор тоже проверяет это условие.

Для решения обратной задачи — нахождения общего уравнения окружности по координатам центра и радиусу — можно использовать калькулятор Уравнение окружности по заданному центру и радиусу в различных формах

Нахождение радиуса круга: формула и примеры

В данной публикации мы рассмотрим, как можно вычислить радиус круга (окружности) и разберем примеры решения задач для закрепления материала.

Формулы вычисления радиуса круга

1. Через длину окружности/периметр круга

Радиус круга/окружности рассчитывается по формуле:

C – это длина окружности/периметр круга; равняется удвоенному произведению числа π на его радиус:

C = 2 π R

π – число, приближенное значение которого равно 3,14.

2. Через площадь круга

Радиус круга/окружности вычисляется таким образом:

S – это площадь круга; равна числу π , умноженному на квадрат его радиуса:

S = π R 2

Примеры задач

Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.

Решение:
Используем первую формулу (через периметр):

Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .

Решение:
Воспользуемся формулой, выраженной через площадь фигуры:

Уравнение окружности

Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности

Равенство (1) есть уравнение окружности радиуса R с центром в точке С.

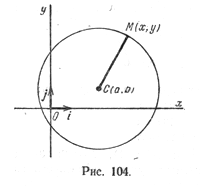
Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.

Так как |СМ| = \( \sqrt <(x — a)^2 + (у — b)^2>\), то уравнение (1) можно записать так:

(x — a) 2 + (у — b) 2 = R 2 (2)

Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение

есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).

Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид

Уравнение (3) называют каноническим уравнением окружности.

Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.

Непосредственной подстановкой значения радиуса в уравнение (3) получим

Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).

Подставив значение координат точки С и значение радиуса в формулу (2), получим

(х — 3) 2 + (у — (—6)) 2 = 81 или (х — 3) 2 + (у + 6) 2 = 81.

Задача 3. Найти центр и радиус окружности

Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.

Задача 4. Доказать, что уравнение

является уравнением окружности. Найти ее центр и радиус.

Преобразуем левую часть данного уравнения:

Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.

Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).

Напишем уравнение прямой АВ:

или 4х + 3y —5 = 0.

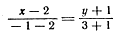
Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:

Напишем уравнение искомой окружности

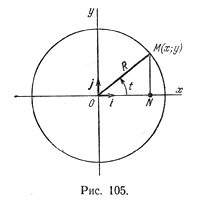
Пусть в прямоугольной системе координат дана окружность x 2 + у 2 = R 2 . Рассмотрим ее произвольную точку М(х; у) (рис. 105).

Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t

(0 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складывая эти равенства почленно, получаем