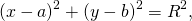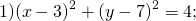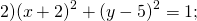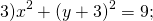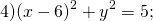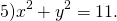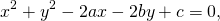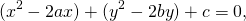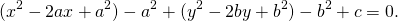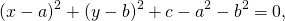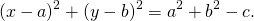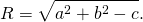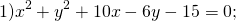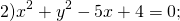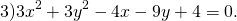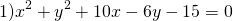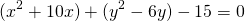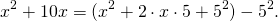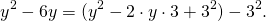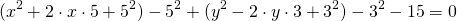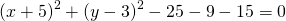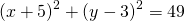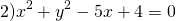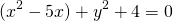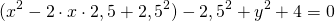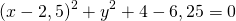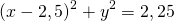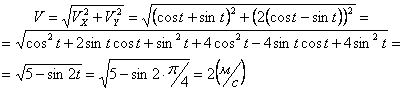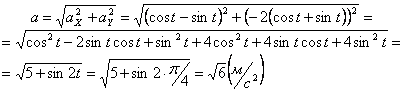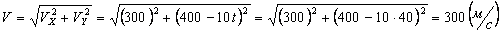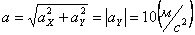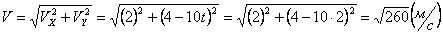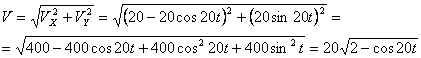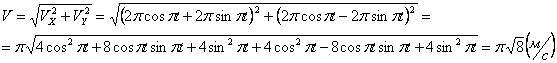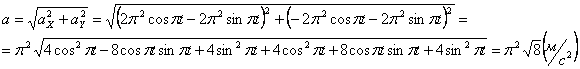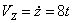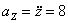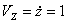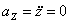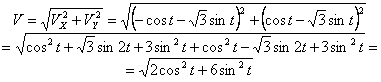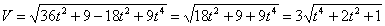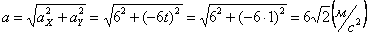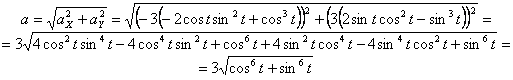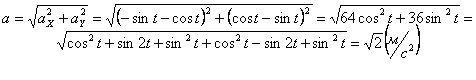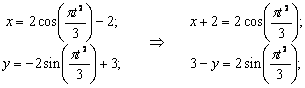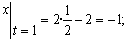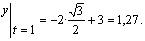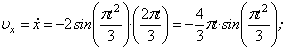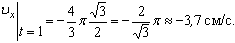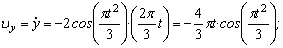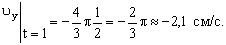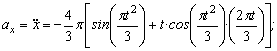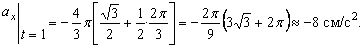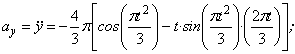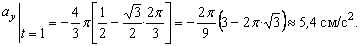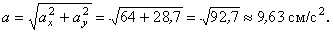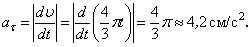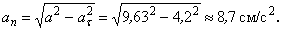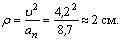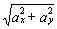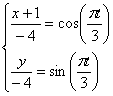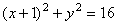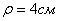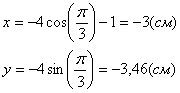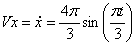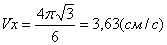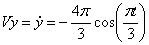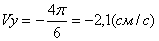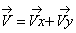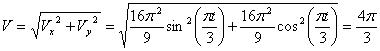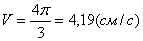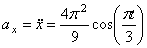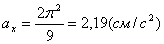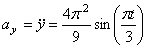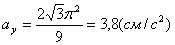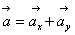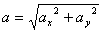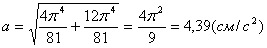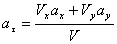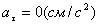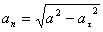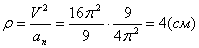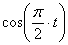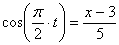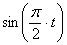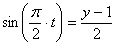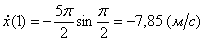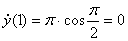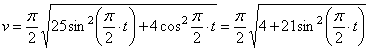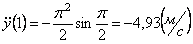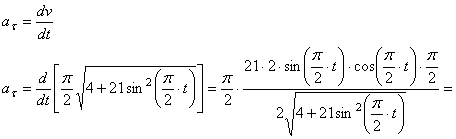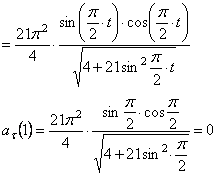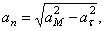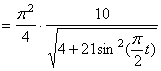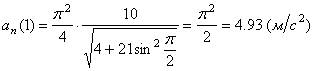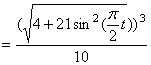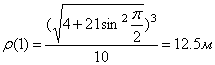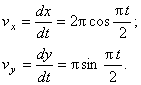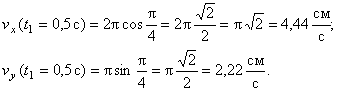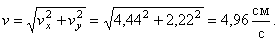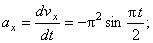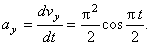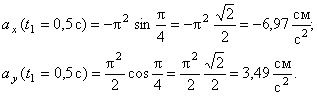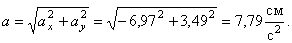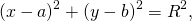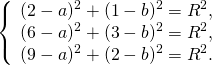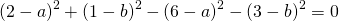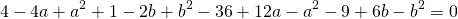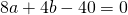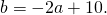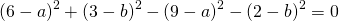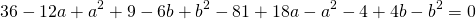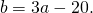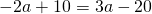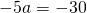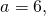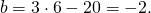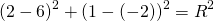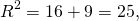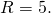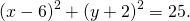T найти радиус если дано уравнение

Как найти радиус окружности если дано уравнение

Нахождение центра и радиуса окружности по общему уравнению окружности

Этот калькулятор проверяет, является ли введенное уравнение общим уравнением окружности, и вычисляет координаты центра и радиуса окружности, если это возможно. Описание способа решения подобных задач находится под калькулятором

Нахождение центра и радиуса окружности по общему уравнению окружности

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Калькулятор выше можно применять для решения задач на уравнение окружности. Чаще всего вы имеете дело с уравнением окружности, выраженном в так называемом стандартном виде

Из этого уравнения достаточно легко найти центр окружности — это будет точка с координатами (a,b), и радиус окружности — это будет квадратный корень из правой части уравнения.

Однако, если возвести в квадрат выражения в скобках и перенести правую часть налево, то уравнение станет выглядеть примерно так:

Это — уравнение окружности в общем виде. Здесь радиус и центр окружности уже не выделены явно, и в задачах обычно просят их найти именно по общему виду уравнения окружности.

Способ решения такого рода задач следующий:

Перегруппируем слагаемые уравнения

Как видим, выражение в конце это уравнение окружности в стандартном виде, из которого уже легко получить и координаты центра окружности и ее радиус. Если же справа получилось отрицательное число — значит заданное вначале уравнение не является уравнением окружности (бывают задачи и на такую проверку). Калькулятор тоже проверяет это условие.

Для решения обратной задачи — нахождения общего уравнения окружности по координатам центра и радиусу — можно использовать калькулятор Уравнение окружности по заданному центру и радиусу в различных формах

Как найти радиус окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать — как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Найти центр и радиус окружности

Если окружность задана уравнением вида

найти центр (a;b) и радиус R такой окружности несложно.

Определить по уравнению окружности координаты её центра и радиуса:

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

Центр окружности — (0;-3), радиус R=3.

Центр — в точке (6;0), радиус R=√5.

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c

Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:

Центром этой окружности является точка (-5;3), радиус R=7.

Центр окружности — точка (2,5;0), радиус R=1,5.

T найти радиус если дано уравнение

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ

7.1. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .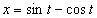

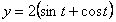
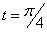
Решение: Скорости точки :

,

,

,

,

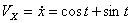
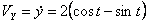
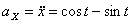
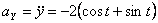
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

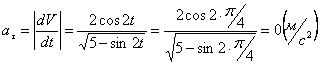
А модуль нормального ускорения:

.

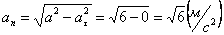
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

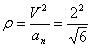
7.2. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .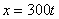

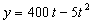
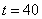
Решение: Скорости точки :

,

,

,

,

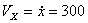
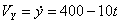
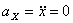
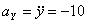
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

А модуль нормального ускорения:

.

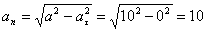
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

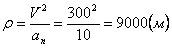
7.3. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .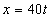

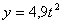
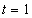
Решение: Скорости точки:

,

,

.

,

,

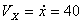
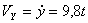
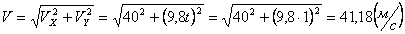
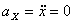
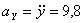
Модуль полного ускорения:

.

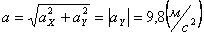
Модуль касательного ускорения точки:

,

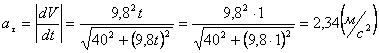
А модуль нормального ускорения:

.

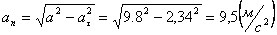
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

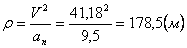
7.4. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .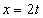

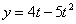
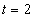
Решение: Скорости точки :

,

,

,

,

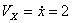
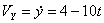
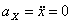
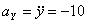
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

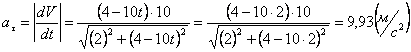
А модуль нормального ускорения:

.

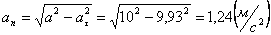
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

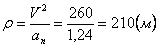
7.5. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .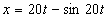

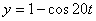
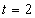
Решение: Скорости точки по осям :

,

,

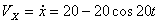
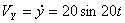
Ускорения точки по осям:

,

,

.

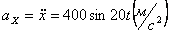
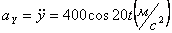
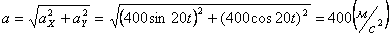
Модуль касательного ускорения точки:

, а модуль нормального ускорения .

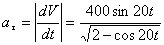
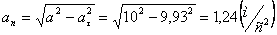
Нормальное ускорение и радиус кривизны траектории связаны соотношением .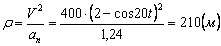

7.6. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .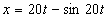

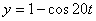
Решение: Скорости точки по осям :

,

,

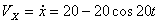
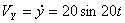
Ускорения точки по осям:

,

,

.

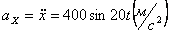
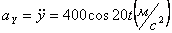
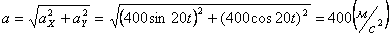
Модуль касательного ускорения точки:

,

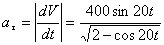
а модуль нормального ускорения:

.

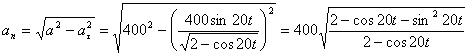
Нормальное ускорение и радиус кривизны траектории связаны соотношением .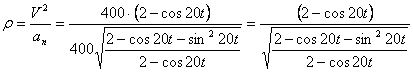

7.7. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .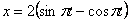

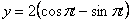
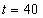
Решение: Скорости точки :

,

,

,

,

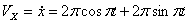
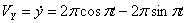
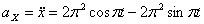
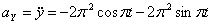
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

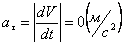
А модуль нормального ускорения:

.

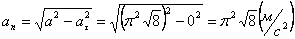
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

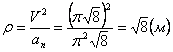
7.8. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .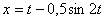

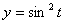
Решение: Скорости точки :

,

,

.

,

,

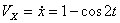
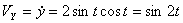
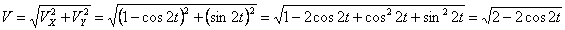
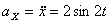
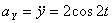
Модуль полного ускорения:

.

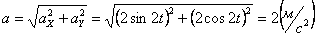
Модуль касательного ускорения точки:

,

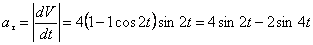
А модуль нормального ускорения:

.

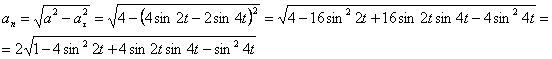
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

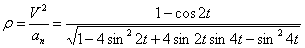
7.9. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , , .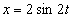

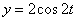
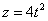
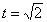
Решение: Скорости точки :

,

,

.

,

,

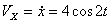
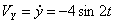
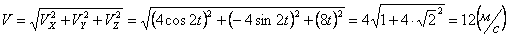
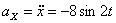
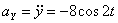
Модуль полного ускорения:

.

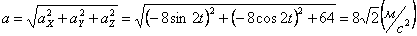
Модуль касательного ускорения точки:

,

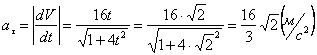
А модуль нормального ускорения:

.

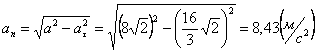
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

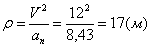
7.10. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .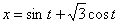

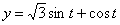
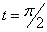
Решение: Скорости точки :

,

,

,

,

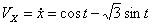
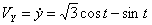
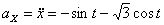
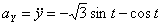
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

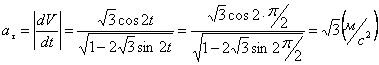
А модуль нормального ускорения:

.

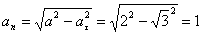
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

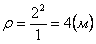
7.11. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .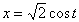

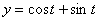
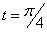
Решение: Скорости точки :

,

,

,

,

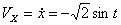
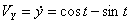
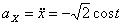
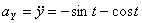
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

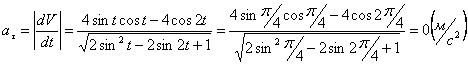
А модуль нормального ускорения:

.

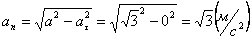
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

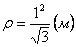
7.12. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , , .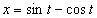

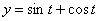
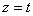
Решение: Скорости точки :

,

,

,

,

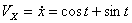
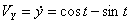
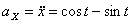
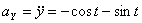
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

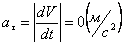
А модуль нормального ускорения:

.

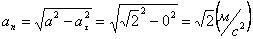
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

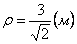
7.13. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .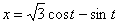

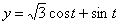
Решение: Скорости точки :

,

,

,

,

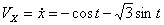
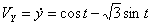
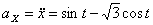
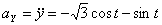
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

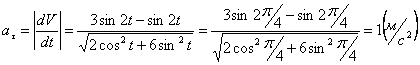
А модуль нормального ускорения:

.

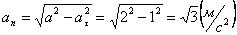
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

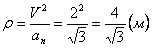
7.14. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .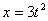

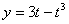
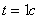
Найти: , , .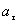

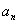
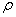
Решение: Скорости точки по осям :

,

,

,

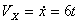
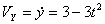
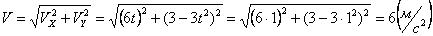
Ускорения точки по осям:

,

,

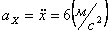
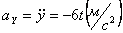
Модуль касательного ускорения точки:

,

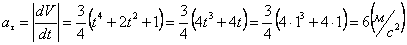
А модуль нормального ускорения:

.

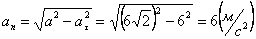
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

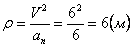
7.15. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .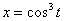

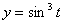
Решение: Скорости точки :

,

,

,

,

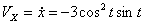
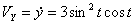
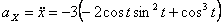
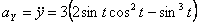
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

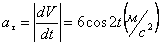
А модуль нормального ускорения:

.

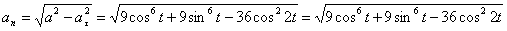
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

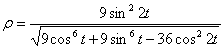
7.16. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .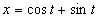

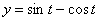
Решение: Скорости точки :

,

,

,

,

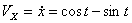
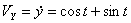
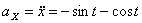
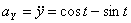
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

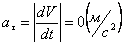
А модуль нормального ускорения:

.

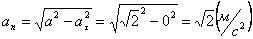
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

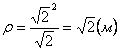
7.17. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .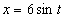

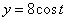
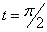
Решение: Скорости точки :

,

,

,

,

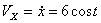
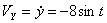
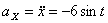
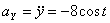
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

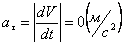
А модуль нормального ускорения:

.

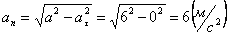
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

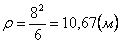
7.18. Дан закон движения точки по окружности радиусом r . Определить:

1) скорость и ускорение точки при 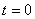и ;

2) моменты остановки точки;

3) путь, пройденный точкой за 10секунд.

Дано: , , , .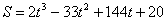

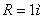
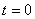
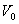
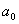
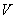
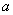
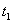
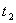
Найти: , , , , , , П.

Решение: 1. На траектории отметим точку О – начало отсчета координаты s и укажем положительное направление отсчета этой координаты. Отметим положение точки в заданные моменты времени: При :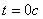

;

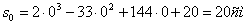
При :

.

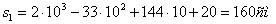
Проведем из этих точек естественные оси координат.

Определим проекцию скорости на касательную:

.

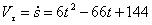
При : ;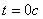

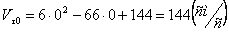
При : .

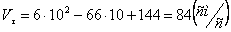
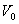
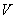
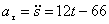
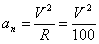
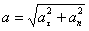
Векторы и совпадают со своими проекциями. Определим проекции ускорения на естественнее оси координат :

; , Полное ускорение точки .

При :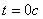

,

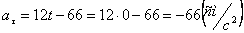
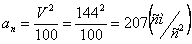
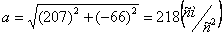
и

.

При :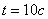

,

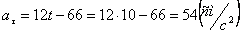
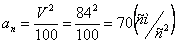
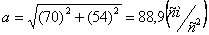
и

.

2. Чтобы найти время остановки надо найти время, когда скорость точки равна нулю:

, получим и .

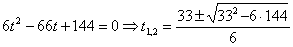
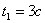
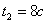
3. Поскольку за 10 секунд точка сделала две остановки, пройденный ею путь за 10с можно найти как сумму пути, пройденного от начала до первой остановки, от первой до второй остановки и от второй до момента времени :

,

; ; ; .

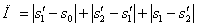
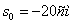
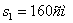
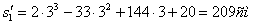
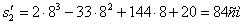
Путь пройденный точкой за 10 секунд:

.

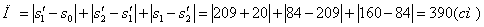
7.19. Определить скорость, касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

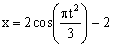
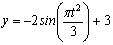
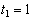
Дано: , (1)

( x и y – в см , t и t ₁ – в с).

Найти: 1) вид траектории;

2) для t = t ₁ положение точки на траектории;

3) .

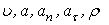
Решение: 1) Уравнение движения (1) можно рассматривать как параметрические уравнения траектории точки. Чтобы получить уравнения траектории в координатной форме, исключаем время t из уравнений (1).

Возводя обе части равенств в квадрат, а затем складывая равенства, получаем 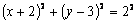, т.е. траекторией точки М является окружность радиуса 2, показанная на рис.1.

2) Определяем положение точки М в заданный момент времени t =1 с :

Вектор скорости точки

. (2)

(3)

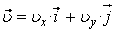
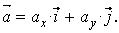
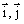
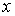
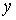
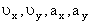
Здесь – орты осей и ; – проекции скорости и ускорения точки на оси координат.

Найдем их, дифференцируя по времени уравнения движения (1):

По найденным проекциям определяем модуль скорости:

, (4)

,

,

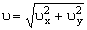
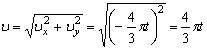
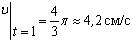
и модуль ускорения точки:

, (5)

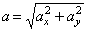
Модуль касательного ускорения точки

, (6)

; (7)

выражает проекцию ускорения точки на направление ее скорости. Знак «+» при означает, что движение точки ускоренное, направление и совпадают; знак «–» – что движение замедленное.

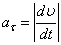
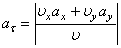
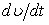
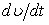
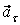
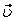
Вычисляем модуль касательного ускорения для заданного момента времени

Модуль нормального ускорения точки

. (8)

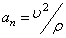
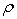
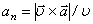
Если радиус кривизны траектории в рассматриваемой точке неизвестен, то нормальное ускорение можно определить по формуле

. (9)

При движении точки в плоскости формула (9) принимает вид

.

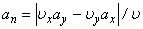
Модуль нормального ускорения можно определить и следующим образом:

. (10)

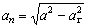
Воспользуемся в нашем случае формулой (10)

Радиус кривизны траектории в рассматриваемой точке определим из выражения:

. (11)

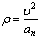
Тогда

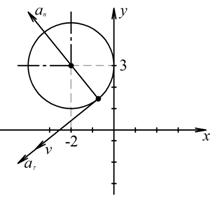
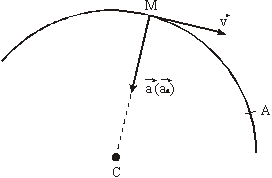
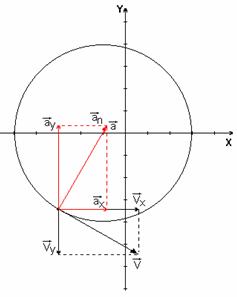
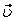
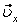
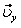
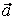
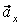
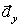
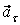
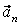
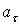
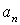
На рис. 1 показано положение точки М в заданный момент времени. Вектор строим по составляющим и , причем этот вектор должен по направлению совпадать с касательной к траектории. Вектор строим по составляющим и и затем раскладываем на составляющие и . Совпадение величин и , найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.

7.20. Определить скорость, касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

( x и y – в см , t и t ₁ – в с).

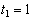
Найти: 1) вид траектории;

2) .

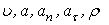
Указания. Задача — относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения. В задаче все искомые величины нужно определить только для момента времени t ₁ = 1 с .

1. Для определения уравнения траектории точки исключим из заданных уравнений движения время t :

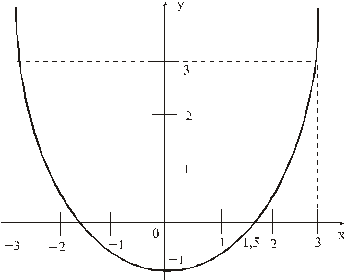
Отсюда окончательно находим уравнение траектории точки (параболы, см. рисунок):

2. Скорость точки найдем по ее проекциям на координатные оси:

V = 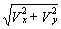и при t ₁ = 1 с,

3. Аналогично найдем ускорение точки:

а =

4. Касательное ускорение найдем, дифференцируя по времени равенство:

. (3)

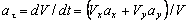
ч исловые значения всех величин, входящих в правую часть выражения (3), определены и даются равенствами (1) и (2).

Подставив в (3) эти числа, найдем сразу, что при t ₁ = 1 с

=7,49 см/с 2 .

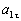
5. Нормальное ускорение точки:

a _n = .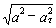

Подставляя сюда найденные числовые значения a ₁ и a _{1 τ} , получим, что при t ₁= 1 с

6. Радиус кривизны траектории ρ = V 2 / a _n .

Подставляя сюда числовые значения V ₁ и a _{1 n} , найдем, что при t ₁ = 1 с

Ответ: V ₁= 8 ,54 см/с, а ₁ =8 см/с 2 , 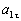=7,49 см/с 2 , a _{1 n} =2,81 см/с 2 , ρ₁ =25,95 см.

7.21. Точка движется по дуге окружности радиуса R =1 м по закону 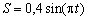( s – в метрах, t – в секундах), где s = AM (см. рисунок).

Найти: скорость и ускорение точки в момент времени t ₁ =1 с .

Определяем скорость точки:

V = ds / dt = .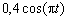

При t ₁ =1 с получим 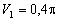= -1,26 м/ с .

Ускорение находим по его касательной и нормальной составляющим:

,

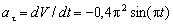
п ри t ₁ = 1 с получим , учтя, что R = 1 м

,

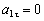
тогда ускорение точки при t ₁ =1 с будет:

=1,59 м/с 2 .

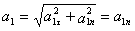
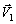
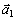
Изобразим на рисунке векторы , , учитывая знак V ₁ и считая положительным направление от А к М.

7.22. По заданным уравнениям движения точки М установить вид её траектории и для момента времени t = t ₁(с) найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а так же радиус кривизны траектории.

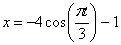
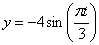
Дано: , , t ₁=1 сек ( x и y – в см , t и t ₁ – в с).

Найти: 1) вид траектории;

2) .

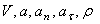
1) Найдём траекторию движения:

Для этого исключим параметр t .

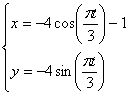
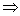
Возведём во вторую степень, получившиеся уравнения, а затем сложим, таким образом, исключится t . Получим:

Это окружность с центром в точке с координатами (-1;0) и радиусом

2) Найдём положение точки на траектории в момент времени t = t _1:

3) Определим скорость токи:

Для нахождения вектора полной скорости необходимо сложить 2 вектора:

Найдём модуль полной скорости:

для момента времени t ₁:

4) Определим ускорение точки:

для момента времени t ₁:

для момента времени t ₁:

Найдём полное ускорение:

Найдём модуль полного ускорения:

для момента времени t ₁:

Определим касательное ускорение :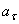

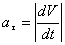
или,

для момента времени t :

Определим нормальное ускорение a_n :

для момента времени t ₁:

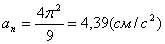
5) Из полученных результатов можно найти радиус кривизны траектории 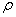, в момент времени t ₁:

Действительно, этот радиус совпадает с радиусом окружности (траектории).

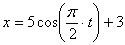
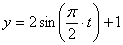
7.23. Точка М движется согласно уравнений ; ; ( x , y — в метрах, t — в секундах). Определить уравнение траектории точки, для момента времени t =1с, найти положение точки, а также скорость, полное, касательное, нормальное ускорения точки и радиус кривизны траектории.

1) Найдем уравнение траектории точки. Для определения уравнения траектории исключим из уравнений движения время . Из первого уравнения движения точки найдем

Из второго уравнения движения найдем

Возведя полученные значения ( правую и левую стороны уравнения ) в квадрат и складывая их находим:

.

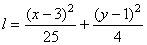
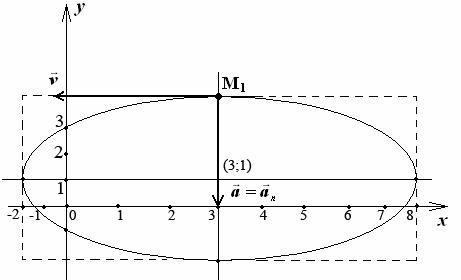
Следовательно, траекторией точки является эллипс с центром в точке с координатами (3;1).

Вид траектории показан на рисунке.

2) Найдем положение точки в момент времени t =1с

; .

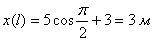
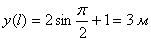
Положение точки М ₁ показано на рисунке.

3) Найдем скорость точки М

,

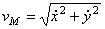
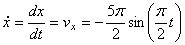
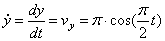
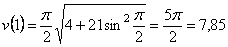
Где , или в момент времени t₁=1c

, или в момент времени t₁=1c

4) Найдём ускорение точки.

,

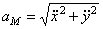
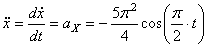
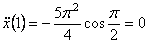
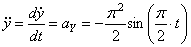
где , или ,

, или

5) Найдем касательное ускорение точки M,

6) Найдём нормальное ускорение точки M ,

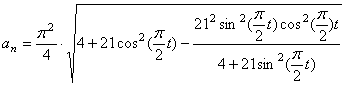
7) Найдем радиус кривизны траектории точки М,

,

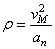
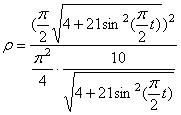
Направление векторов показано на рисунке.

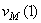
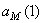
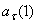
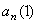
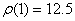
Ответ: =7.85м/ c ; = 4.93 м/ c 2 ; =0; = 4.93 м/ c 2 ; м

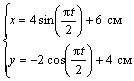
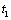
7.24. Пусть точка М движется в плоскости xOy в соответствии с уравнениями . Для момента времени = 0,5 с найти положение точки М на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.

Решение: Заданный закон движения точки в координатной форме можно рассматривать как параметрические уравнения траектории точки. Исключим время t из уравнений движения и получим уравнение траектории точки в виде:

.

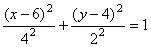
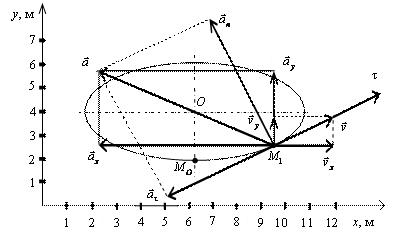
Таким образом, траекторией точки М является эллипс со смещенным центром, изображенный на рис. Отметим на траектории положение точки М ₁ ( x ₁, y ₁) в момент времени t ₁ = 0,5 c

;

.

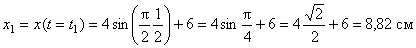
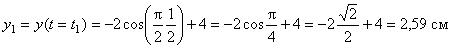
Вектор скорости точки представим в виде:

,

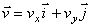
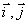
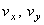
где – орты координатных осей О x и О y ; – проекции вектора скорости точки на координатные оси, которые равны 1-м производным от соответствующих координат по времени

В момент времени t ₁ = 0,5 c

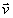
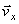
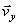
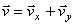
Вектор скорости точки строим по двум взаимно перпендикулярным проекциям и в соответствии с выбранным масштабом

.

Полученный вектор должен быть направлен по касательной к траектории точки в сторону движения. Модуль скорости точки определим по уже найденным проекциям

Вектор ускорения точки представим в виде:

,

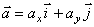
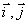
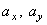
где – орты координатных осей О x и О y ; – проекции вектора скорости точки на координатные оси, которые равны 1-м производным от проекций вектора скорости или 2-м производным от соответствующих координат по времени:

В момент времени t ₁ = 0,5 c

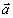
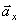
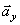
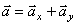
Вектор ускорения точки строим по двум взаимно перпендикулярным проекциям и в соответствии с выбранным масштабом

.

Полученный вектор ускорения точки в общем случае должен отклоняться от вектора скорости в сторону вогнутости траектории, а при движении по эллипсовидной траектории – проходить через центр эллипса. Модуль ускорения точки определим по уже найденным проекциям

Вектор полного ускорения точки можно также представить в виде геометрической суммы его проекций на оси естественной системы отсчета

,

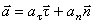
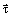
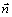
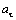
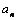
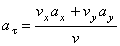
где и – единичные орты касательной и главной нормали; и – соответственно проекции вектора ускорения на касательную и главную нормаль. Касательную М ₁ t направляем по касательной к траектории в сторону движения точки движения, а главную нормаль М₁ n – перпендикулярно касательной в сторону вогнутости траектории. При вычислении касательного ускорения удобно воспользоваться формулой, устанавливающей связь между координатным и естественным способами задания движения точки

.

В момент времени t ₁ = 0,5 c

.

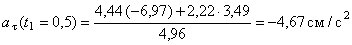
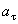
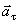
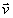
Значение касательного ускорения имеет отрицательный знак, следовательно, в данный момент времени движение точки замедленное и вектор касательного ускорения направлен в противоположную сторону направлению вектора скорости точки .

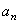
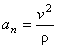
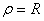
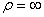
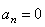
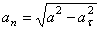
Нормальное ускорение вычислим по формуле , если известен радиус кривизны траектории. Например, если точка движется по окружности радиусом R, то в любой точке траектории . Если же траекторией движения точки является прямая, то , следовательно, . В данном случае радиус кривизны траектории заранее не известен, поэтому нормальное ускорение определяем по формуле:

.

В момент времени t ₁ = 0,5 c

.

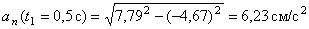
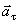
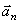
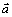
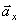
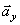
Построим векторы и в соответствии с уже выбранным масштабом, а затем сложим их геометрически. В результате получим тот же вектор полного ускорения точки , который ранее уже был получен геометрической суммой составляющих и . Этот факт служит контролем правильности решения.

Радиус кривизны траектории в рассматриваемой точке определим по формуле

.

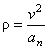
В момент времени t ₁ = 0,5 c

.

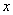
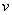
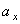
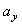
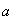
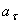
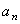
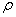
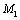
Ответ: =8,82 см; =2,59 см; =4,44 см/ c ; =2,22 см/ c ; =4,96 см/с; =6,97 см/с 2 ; =3,49 см/с 2 ; =7,79 см/с 2 ; =4,67 см/с 2 ; =6,23 см/с 2 ; =3,95 см (радиус кривизны траектории в точке ).

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Уравнение описанной окружности

Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?

Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.

Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).

Подставив координаты вершин треугольника в уравнение окружности

получим систему уравнений

Вычтем из первого уравнения системы второе:

Теперь из второго уравнения системы вычтем третье:

Приравняем правые части равенств b=-2a+10 и b=3a-20:

Подставим в первое уравнение системы a=6 и b=-2:

a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности

Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.