Tds du pdv уравнение называется

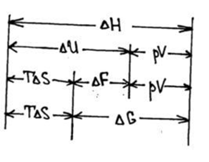
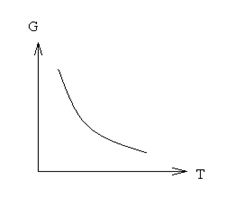
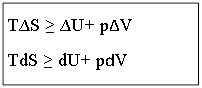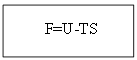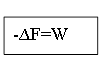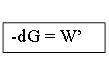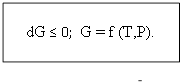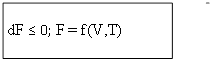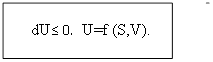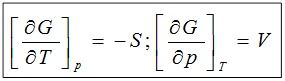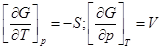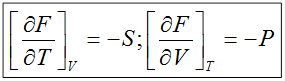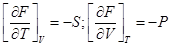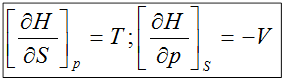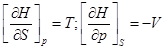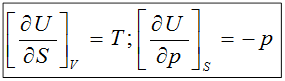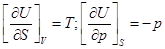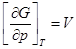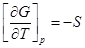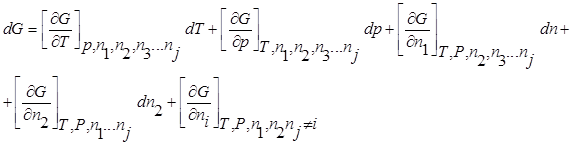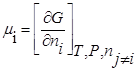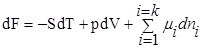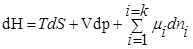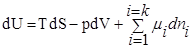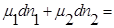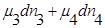Свойства энтропии. Объединенная формулировка I и II законов термодинамики: TdS>dU+pdV.

Основные понятия

Законы, принципы и соотношения

TdS>dU+pdV

Некоторые важнейшие свойства энтропии замкнутых систем

Свойства энтропии.

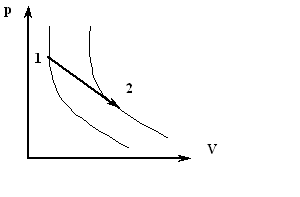
1. Итак, энтропия — функция состояния . Если процесс проводят вдоль адиабат, то энтропия системы не меняется. Значит адиабаты -это одновременно и изоэнтропы . Каждой более «высоко» расположенной адиабате (изоэнтропе) отвечает большее значение энтропии. В этом легко убедиться, проведя изотермический процесс между точками 1 и 2 , лежащими на разных адиабатах (*см. рис.).

В этом процессе Т=const , поэтому S2-S1=Q/T . Для идеального газа Q равно работе А , совершаемой системой. А так как А>0 , значит S₂>S₁ .

Таким образом, зная, как выглядит система адиабат. Можно легко ответить на вопрос о приращении энтропии при проведении любого процесса между интересующими нас равновесными состояниями 1 и 2 .

2. Энтропия- величина аддитивная : энтропия макросистемы равна сумме энтропий ее отдельных частей.

3. Одно из важнейших свойств энтропии заключается в том, что энтропия замкнутой (т.е. теплоизолированной) макросистемы не уменьшается — она либо возрастает, либо остается постоянной . Если же система не замкнута, то ее энтропия может как увеличиваться, так и уменьшаться.

Принцип возрастания энтропии замкнутых систем представляет собой еще одну формулировку второго начала термодинамики. Величина возрастания энтропии в замкнутой макросистеме может служить мерой необратимости процессов, протекающих в системе. В предельном случае, когда процессы имеют обратимый характер, энтропия замкнутой макросистемы не меняется.

Пример. Идеальный газ, находящийся в некотором состоянии, адиабатически (т.е. без теплообмена) расширили до объема V. Одинаково ли будет установившееся давление газа в конечном состоянии (в объеме V), если процесс расширения
а) обратимый,
б) необратимый?

В соответствии с принципом возрастания энтропии в замкнутой системе при необратимом процессе энтропия должна увеличиться. Значит установившееся состояние будет соответствовать точке на более высокой адиабате, т.е. давление будет больше.

Заметим, что с самого начала введение понятия энтропии S было поставлено в прямую связь с необратимостью. Оказывается, все самопроизвольно протекающие процессы в природе — от теплообмена до химических реакций — протекают так, что энтропия возрастает. Необходимо специальное взаимодействие с окружающей средой, что бы препятствовать возрастанию энтропии в макросистеме. Наиболее ярким примером могут служить все живые существа.

Объединенное выражение Iи II— закона термодинамики

ЭНТРОПИЯ, КАК КРИТЕРИЙ НАПРАВЛЕННОСТИ

Рассмотрим изолированную систему.

В изолированной системе : Q= 0

Обратимый процесс: , .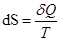

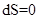
Необратимый процесс: , .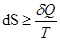

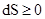
В изолированной системе все самопроизвольные процессы идут в направлении увеличения энтропии системы, и пределом процесса является max. и постоянное значение энтропии.

В неизолированных системах энтропия может возрастать, убывать и быть постоянной, поэтому не является критерием направленности протекания самопроизвольных процессов.

ЭНЕРГИЯ ГИББСА И ЭНЕРГИЯ ГЕЛЬМГОЛЬЦА

TdS≥dU+pdV; dU- TdS+pdV=0.

1. Энергия Гельмгольца (Т=const, V=const)

При V=const: dU- TdS≤0

dU- TdS — SdT≤- SdT

При Т=const: dU- d(TS) ≤ 0;

При постоянном объеме и температуре все самопроизвольные процессы идут в сторону уменьшения энергии Гельмгольца до её постоянного min-ого значения.

2. Энергия Гиббса (Т=const, Р=const)

При постоянном давлении и температуре все самопроизвольные процессы идут в сторону уменьшения энергии Гиббса до его постоянного min-ого значения.

δW=TdS-dU —обратимый процесс.

Убыл энергии Гельмгольца равна max работе процесса.

δW’= TdS – dU- pdV(обр)

Убыл энергии Гиббса равна max полезной работе процесса.

КАК КРИТЕРИЙ САМОПРОИЗВОЛЬНОГО ПРОЦЕССА

1) dG = dU–TdS –SdT+pdV+Vdp;

dG ≤ TdS- pdV — TdS –SdT +pdV+Vdp;

2) dF = dU–TdS –SdT;

dF ≤ TdS-pdV–TdS –SdT;

dH ≤ TdS-pdV +pdV+Vdp;

ТЕРМОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ

Это функции, с помощью которых или их частных производных можно выразить в явном виде параметры состояния.

1) ;

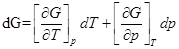
2) ;

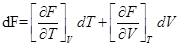
3) ;

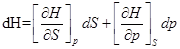
4) ;

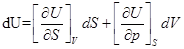
Функции энергии Гиббса, Гельмгольца, энтальпия и внутренней энерги являются характеристическими.

Поясним их смысл:

2.

Подставим вместо энтропии ее значение через частную производную энерги Гиббса и Гельмгольца:

Тогда, уравнение Гиббса-Гельмгольца для системы:

Уравнение Гиббса-Гельмгольца для процесса:

Эти уравнения показывают изменение энергии Гиббса и Гельмгольца при изменении температуры, также они связывают энергию Гельмгольца с тепловыми эффектами процесса(∆U и ∆F). При этом энтропия в явном виде не используется.

dG = –SdT+Vdp, G = f (T,P)—уравнение справедливо, если система является закрытой и в ней не идет химическая реакция (состав системы не меняется).

Энергия множества переменных (компонентов), которые рассматриваются как независимые переменные: G =f (T,P,n₁,n₂,n₃…n_i).

Химическим потенциалом данного компонента называется частная производная соответствующей термодинамической функции по числу молей данного компонента при условии постоянства параметров, функцией которых данная термодинамическая функция является.

Химический потенциал — это есть изменение энергии Гиббса (или любой другой термодинамической функции) при введении в большой энергии системы 1 моля данного вещества.

,где к— число компонентов.

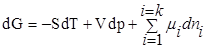
При T=const, P=const

,

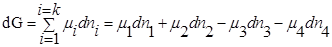
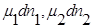
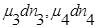
где — продукт, а — исходные вещества.

Для индивидуального вещества химический потенциал равен соотвественно термодинамической функции (в частности энергии Гиббса).

Химический потенциал компонента тождественен мольной энергии Гиббса. Для определения мольной энергии Гиббса i-ого компонента в условиях, отличных от стандартных, можно воспользоваться соотношением, которое справедливо для идеальных газов G _i не зависит от вида и концентрации других компонентов:

— (для газов)

— стандартный химический поненциал; P_i — парциальное давление данного компонента.

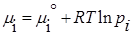
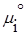
Т =298К, Р= 1атм, R=8,314 Дж/(моль*К),

Парциальное давление — это объем одного газа, который занимал бы вес объём данного газа. ∑p_i=p

, где — мольная доля компонентов в растворе.

Дата добавления: 2016-02-02 ; просмотров: 1228 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Параметры состояния в термодинамике и первый закон термодинамики (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8

Расчет основных термодинамических величин ΔU, Q, W.

В предыдущей лекции первый закон термодинамики, будучи специализированной формой записи закона сохранения энергии, был записан в виде:

du = Tds – pdv (2.1)

Здесь приращение внутренней энергии выражено через параметры состояния рабочего тела: термические T и s и деформационные р и v. Первое слагаемое в (2.1) справа представляет собой количество термического взаимодействия между внешней средой и рабочим телом dq = Tds, т. е. количество теплоты, подведенной (отведенной) к рабочему телу. Второе – количество деформационного взаимодействия между внешней средой и системой, т. е. работу сжатия (расширения) dw = pdv. Поэтому иногда удобно записывать первый закон термодинамики (2.1) в виде:

где слева характеристика энергии системы, а справа – количества воздействий внешней среды на систему.

В основном уравнении термодинамики (2.2) фигурируют три величины. Чтобы это уравнение стало расчетным инструментом термодинамики, необходимо дать правила независимого расчета по крайней мере двух величин из трех, входящих в (2.2). Начнем с анализа функции u(s, v).

1. Термодинамические характеристические функции

1.1. Внутренняя энергия и ее основное свойство.

Рассмотрим интеграл по замкнутому контуру (циклу) от основного уравнения (2.2)

и обратимся к рисунку (2.1).

Рис. 2.1. Иллюстрация к пояснению полноты дифференциала du.

Пусть процесс начинается в состоянии (точке) 1, доходит до состояния (точки) 2 и завершается снова в точке 1. Из определения понятия уравнения состояния следует, что

T = T(s, v) и p = p(s, v).

Эти же аргументы относятся к функции (см. (2.1)) u = u(s, v), т. е. u(∙) зависит только от координат (параметров) состояния s и v термодинамической системы, и это естественно с физической точки зрения – ее возврат в исходное состояние (точка 1), где внутренняя энергия имеет только одно определенное значение. Следовательно, для замкнутых (круговых) процессов – в термодинамике они названы циклами:

(2.3)

Поэтому из математического анализа (из теории функций многих переменных) следует, что du – полный дифференциал и изменение функции Δu в любом процессе 1 — 2

u2 –u1 = (2.4)

или в графической форме — при переходе от точки 1 к точке 2 — не зависит от траектории процесса перехода из точки в точку (см. рис 2.2), а в действительных явлениях характер процесса не влияет на изменение внутренней энергии – оно определяется только состоянием (параметрами) в начале и конце процесса.

Рис. 2.2. Изменение внутренней энергии u(s, v) не зависит

от траектории F(s, v) = 0 перехода из точки 1 в точку 2.

Определение. Величины (функции), изменение которых не зависят от характера процесса, а определяются только состояниями (параметрами) начала и конца процесса, называются функциями состояния.

Вновь вернемся к первому закону термодинамики, записанного через параметры состояния (2.1). Справа и слева в уравнении (2.1) прибавим полный дифференциал d(pv) и проведем простые преобразования:

du + d(pv) = Tds – pdv + d(pv) → d(u + pv) = Tds + vdp → dh = Tds + vdp. (2.5)

Эта цепочка равенств — справедлива, т. к. сумма полных дифференциалов равна дифференциалу суммы функций, а d(pv) = pdv + vdp по правилу дифференцирования произведения функций. В (2.5) мы приняли, что

h ≡ u + pv, Дж/кг или Дж/кмоль. (2.6)

Это тождество по существу является определением новой функции h(s, v), которая по построению является функцией состояния и стандартизованно ее называют энтальпией (ранее в термодинамике называлась теплосодержанием).

1.3. Свободная энергия и свободная энтальпия.

Проделаем процедуру перестановки переменных – термических параметров еще два раза:

du – d(Ts) = Tds – pdv – d(Ts) → d(u – Ts) = — sdT – pdv → df = — sdT – pdv. Дж/кг (2.7.1)

dh – d(Ts) = Tds + vdp – d(Ts) → d(h –Ts) = — sdT + vdp → dg = — sdT + vdp. Дж/кг (2.7.2)

Здесь, как и раньше, от обеих частей уравнений (2.1) и (2.5) вычли одну и туже величину d(Ts), снова воспользовались свойствами дифференциалов и дифференциалом произведения функций.

Функция f(s, v) ≡ u — Ts (ее в термодинамике называют свободной энергией или по стандарту — функцией Гельмгольца) является функцией состояния, а df – является полным дифференциалом. Функция g(s, v) ≡ h – Ts ≡ u + pv – Ts (ее в термодинамике называют свободной энтальпией или по стандарту — функцией Гиббса) также является функцией состояния, а ее дифференциал dg – полный.

Эти термодинамические характеристические функции (или термодинамические потенциалы) широко используются при анализе химических и фазовых превращений, при определении направления этих превращений и их полноты. Численные значения Δu и Δh можно получить, зная свойства рабочего тела (вещества) или аналитические связи канонически сопряженных параметров T – s и p – v, что будет сделано в §2.2 и §3.

Не будет преувеличением назвать эти 4 характеристические функции фундаментальными, т. к. в совокупности их можно отнести к так называемому «первому закону термодинамики» полностью качественно (по видам взаимодействия) и количественно (по возможности через них расчета процессов: параметров состояния, изменения энергии рабочих тел, количеств внешних воздействий). Так как общее число внешних воздействий равно двум, то количество характеристических функций равно ровно четырем.

Сведем эти результаты в таблицу для пущей наглядности.

Функция состояния Дж/кг

Полный дифференциал через параметры состояния

Свободная энергия (функция Гельмгольца)

Свободная энтальпия (функция Гиббса)

Замечание. Обращаем внимание, что при выводе функций состояния h, f и g центральную роль играет внутренняя энергия u(s, v), первый закон термодинамики и полнота дифференциала du. В инженерно-технических расчетах чаще всего используется внутренняя энергия u и энтальпия h. Их изменение в процессах (Δu и Δh) равно количеству соответствующего внешнего воздействия. Так, при s = const величина Δu равна работе w адиабатического процесса, при v = const величина Δu равна количеству теплоты q. При p = const количество теплоты q равно величине Δh. Таким образом, через приращения функций состояния вычисляются количества внешних воздействий (функций процесса). Уравнения для расчета Δu и Δh будут выведены в разделе 3.

1.4. Дифференциальные соотношения термодинамики.

Каждое из четырех дифференциальных выражений может служить для вывода связи параметров состояния. Эти связи в термодинамике называются «Уравнениями Максвелла» или дифференциальными соотношениями. Действительно, если u = u(s, v), то

du = (∂u/∂s)vds + (∂u/∂v)sdv и du = Tds – pdv.

Отсюда: T = (∂u/∂s)v и — p = (∂u/∂v)s.

В математическом анализе существует теорема о равенстве вторых смешанных производных. Тогда

Это уравнение связи четырех термодинамических параметров в технике или в природе и характеризует количественно равенство двух совершенно разных физических эффектов: изменение температуры Т при изменении удельного объема v в адиабатно-изоэнтропийном процессе численно такое же, как изменение давления p при изменении энтропии s (т. е. при равновесном теплообмене) в изохорном процессе. Получить такую взаимосвязь иным, т. е. не термодинамическим, способом в принципе невозможно.

Предлагаем студентам для тренировки самостоятельно вывести еще 3 дифференциальных соотношения из выражений для dh, df, dg.

По существу, единственная содержательная суть термодинамики – это первый закон термодинамики + диффсоотношения! А где она применяется (техника, химия, электро-магнитные процессы, коммерческие фирмы, коммерческие банки и т. д.) – дело прикладников термодинамики.

2. Внешние воздействия (функции процесса).

Если справедливо (2.3), то для замкнутого контура процессов (цикла)

,

т. е. сумма внешних теплот за цикл равна сумме внешних работ, а это может быть не только при нулевых слагаемых справа. Рассмотрим рис.2.3 и прейдем к процессам 1 – а – 2 и 2 – в – 1:

Рис. 2.3. Иллюстрация неполноты дифференциалов dq и dw.

;

. (2.8)

Здесь просто интеграл по замкнутому контуру разбили на два обычных интеграла: сначала интегрируем от точки 1 к точке 2 по траектории «а», потом обратно от точки 2 к точке 1 по траектории «в». И провели изменение направления интегрирования во втором интеграле. Из математического анализа известно, что геометрический смысл определенного интеграла от любой интегрируемой функции – это площадь под графиком этой функции. Обращаясь снова к рис. 2.3, видно, что интеграл по замкнутому контуру от количеств внешних воздействий dq и dw равен площади замкнутого контура (цикла) в соответствующих координатах. Наверное, понятно, что эта площадь сильно зависит не только от координат точки 1 и точки 2, но и от вида (формы) самих траекторий перехода из т. 1 в т.2 и обратно. Особенно это наглядно видно на рис.2.4.

Рис. 2.4. Иллюстрация зависимости количества теплоты q и работы w

от траектории пути процесса перехода из состояния т.1 в состояние т. 2.

Разная штриховка соответствует разным траекториям (процессам).

Из рассмотренного следует, что интеграл ∫dw (сумма элементарных количеств работы) и, аналогично, ∫dq (сумма элементарных количеств теплоты) зависят от вида траектории при неизменных начальных и конечных состояниях процесса.

Определение. Величины (функции), изменение которых зависят не только от состояния (параметров) начала и конца процесса, но и еще от траектории, называются функциями процесса.

Заключение: внутренняя энергия u = u(s, v) является функцией состояния, а теплота q и работа w являются функциями процесса (как, впрочем, и любое другое внешнее воздействие – электрическое, химическое, массообменное и т. д.).

Замечание. В различных учебниках, монографиях, учебных пособиях по технической термодинамике подчас вводят специальное обозначение для приращений теплоты и работы в виде δq и δw вместо dq и dw, как в этих лекциях, как бы подчеркивая, что это элементарные приращения, а не полные дифференциалы.

2.1. Расчет количества теплоты и теплоемкости.

Потребность в расчетах количества теплоты в научной и инженерной практике появилась задолго до «рождения» термодинамики. Эта потребность стимулировала появление специальной науки – калориметрии, в которой центральным понятием является понятие теплоемкости. Исторически термин «емкость теплоты» перешел в «теплоемкость», которая различается по многим характеристикам.

Определение. Истинной теплоемкостью вещества называется отношение бесконечно малого количества теплоты к бесконечно малому изменению температуры:

Дж/К (2.9)

Смысл слова «истинная» состоит в том, что бесконечно малое приращение температуры dT берется от какой-то температуры Т. Поэтому истинная теплоемкость является функцией от самой температуры (параметр, влияющий на свойства вещества).

Наверное, понятно, что при одном и том же изменении температуры dT элементарное количество теплоты dQ и, следовательно, теплоемкость при таком изменении зависят от количественной меры вещества. В химической технологии – это число молей (кмоль), в технике и быту количество вещества определяют или массой m (кг), или объемом V0 при нормальных условиях (нм3)(в химии р0 = 760 мм. рт. ст, Т0 = 298К). Поэтому истинную теплоемкость относят (уделяют) на одну из этих мер. Соответственно, получается удельная истинная теплоемкость массовая, мольная и объемная. Их обозначения (не стандартизованы) и размерность следующие: [c] = Дж/кгК, [μc] = Дж/кмольК, [c΄] = Дж/нм3К.

Определение. Средней теплоемкостью называется

, ΔT = t2 – t1 (2.10)

Индекс «m» внизу у значка теплоемкости присвоен для обозначения слова «средний» (от английского слова middle или немецкого mittel). По существу, средняя теплоемкость – это средне интегральная величина истинной теплоемкости.

Иными словами, средняя теплоемкость вещества в каком-то интервале температуры – это количество теплоты, которое надо подвести (отвести) к (от) рабочему телу, чтобы изменить его температуру на 1 градус.

Так как удельное (полное) количество теплоты q (Q) является функцией процесса, то в калориметрии пришлось отдельно рассматривать теплоемкости по процессам: изохорную (v = const) и изобарную (p = const), так как эти процессы наиболее часто применяются на практике (емкости, трубы, аппараты и т. д.) Обозначение этих теплоемкостей (калорических величин) следующее: ср, сv или , для истинных и средних теплоемкостей соответственно.

В итоге выстраивается обширная классификация теплоемкостей: по интервалам температур на истинные и средние, по количествам вещества на массовые, мольные и объемные; по свойствам самих веществ; и, наконец, по множеству видов процессов, среди которых чаще всего встречаются изохорный и изобарный. Это численное и содержательное обилие теплоемкостей требует внимательного отношения к символам и размерностям рассмотренной калорической величины. Мы рекомендуем студентам в своей учебной работе всякий раз четко понимать и обозначать, о какой же теплоемкости в их расчетах идет речь (а их оказалось 7 видов без учета свойств веществ, а с ними и номенклатуры теплоемкостей). При любых расчетах всегда надо указывать размерность и номенклатуру (т. е. название) используемой теплоемкости.

Тогда удельное количество теплоты находится как:

q = ΔT, Дж/кг, q = μ ΔT, Дж/кмоль, и q = ΔT, Дж/нм3.

А полное количество теплоты находится как:

Q = mq = m ΔT, Q = nq = n μΔT, Q = V0q = V0 ΔT, Дж.

Соотношение теплоемкостей, отнесенных к разным количествам вещества следующее:

μс = μ∙с = с΄∙22,4 кДж/кмольК. (2.11)

Примечание: конкретное освоение и расчет теплоемкостей рассматривается на лабораторной работе №2 «Определение объемной теплоемкости воздуха при постоянном давлении».

. Существуют многочисленные табличные данные в справочной литературе по этим величинам теплоемкостей. Но для прикидочных расчетов, в которых нет особых требований к точности результата, полезно пользоваться постоянными величинами теплоемкостей, которые приводятся в таблице ниже.

Таблица приближенных значений мольных

теплоемкостей газов при невысоких температурах.

Трех и более атомный

Окончательно: теплоемкость, как калорическая (тепловая) величина, не относится к категории функций состояния и тем более к параметрам состояния. Строго говоря, понятие теплоемкости чуждо термодинамике, так как количество термического воздействия внешней среды на систему можно рассчитать и без теплоемкости как dq = Tds. Тем не менее обилие справочного материала по теплоемкости для большого числа веществ и привычка к этой калорической характеристике сделали ее широко употребительной в термодинамических и других физико-химических расчетах.

Теперь с помощью простых физических соображений покажем, что изобарная теплоемкость любого вещества всегда больше изохорной (ср > cv).

Сначала проведем мысленный эксперимент, как бы используя экспериментальную установку на рис.2.5.

Рис.2.5. Схема двух экспериментов.

Измеряемые величины: температура Т с помощью термопар,

давление р с помощью манометра, количество теплоты q.

В первом случае (слева) просто нагреваем баллон с газом, во втором – нагреваем и поддерживаем постоянное давление в сосуде, позволяя газу расширяться. Зададимся вопросом: «В каком случае необходимо подвести больше теплоты, если начальная температура Т и ее изменение ΔТ в обоих случаях одинаковы?». Или иначе: «Какая теплоемкость больше: ср или сv?».

Ответ основывается на принципиальном различии экспериментов: слева термодинамическая система деформационно изолирована от внешней среды, т. е. не может совершить работу dw = pdv, а справа – может. И газ по-прежнему нагревается на ΔТ от подведенной теплоты qv = cvΔT, а во втором случае qp = qv(ΔT) + q(w) ≡ cpΔT. Поэтому ответ на поставленный вопрос: ср > сv.

2.2. Расчет количества теплоты и энтропия.

Из лекции 1 и анализа определения теплоемкости понятно, что количество теплоты можно определить двояко – через теплоемкости и через энтропию. Действительно, dq = cdT или dq = Tds, т. е. cdT = Tds, а переходя на геометрическую интерпретацию определенного интеграла ∫dq, как площади под кривой, можно воспользоваться тепловыми диаграммами с координатами с – Т или Т – s (см. рис. 2.6.).

Рис.2.6. Тепловые диаграммы с – Т и Т – s для некоторого вещества.

Заштрихована площадь, численно равная количеству теплоты.

Разумеется, вторая, т. е. Т – s диаграмма, более содержательна и строга, т. к. она имеет координаты в виде функций состояния. Остается для интегрирования выразить T через s (или сх через Т), что возможно при известных свойствах веществ.

3. Термодинамические свойства веществ.

3.1. Свойства веществ и расчет внутренней энергии и энтальпии.

Ранее мы получили важный результат: внутренняя энергия u(s, v) является функцией координат состояния s и v. С другой стороны имеем уравнение состояния рабочего тела, предоставленное физиками, T = T(s, v). Из этого уравнения ничто не мешает найти энтропию s = s(T, v) и подставить ее в зависимость для u(s, v). Получим новую зависимость u(s(T, v),v) = u(T, v) и для последней распишем полный дифференциал внутренней энергии du:

du = (∂u/∂T)vdT + (∂u/∂v)Tdv. (2.12)

Еще запишем основное уравнение термодинамики в двух формах (см. лекцию 1):

dq = du +dw, или dq = du + pdv, где dq =схdT в произвольном процессе.

Пусть х = v = const, т. е. конкретизируем изохорный процесс (dv = 0), и тогда схdT = cvdT = du, т. е.

После подстановки этого выражения в (2.12) получаем:

du = cvdT + (∂u/∂v)Tdv. (2.13)

Получили очень важный результат в виде (2.13) — уравнение для расчета изменения внутренней энергии. Если рассмотреть еще энтальпию h(s, v), снова сделать замену переменных h(T, p) с помощью уравнений состояния, далее провести процесс х = p = const над рабочим телом, то получим уравнение для расчета изменения энтальпии:

dh = cpdT + (∂h/∂p)Tdp. (2.14)

Предлагаем студентам проделать эту процедуру.

Уравнения (2.13) и (2.14) справедливы для любых веществ и любых процессов c рабочим телом.

3.1.1. Идеальный газ.

Определение. Идеальным газом называется такое состояние вещества, при котором можно пренебречь силами взаимодействия между молекулами этого вещества.

В этом определении понятия идеального газа подчеркивается, что одно и тоже вещество может быть в любом состоянии, в том числе и в состоянии идеального газа. Например, воздух при обычных условиях (давление и температура – атмосферные) – является идеальным газом. Тот же воздух в жидком состоянии уже не идеальный газ. Пары воды в составе атмосферного воздуха – идеальный газ, а вода в состоянии близком к кипению или конденсации – нет.

В первой лекции было дано определение понятия уравнения состояния: это функциональная зависимость потенциала взаимодействия системы какого-то рода от всех координат состояния. Для термодеформационной системы (а это и есть предмет изучения технической термодинамики) имеем ровно два уравнения состояния:

T = T(s, v) и p = p(s, v). (2.15.1)

Конкретный вид этих зависимостей предоставляют физики для каждого индивидуального рабочего тела (вещества).

Как показано в лекции 1, можно провести несложную замену переменных:

T = T(s, v) → s = s(T, v) → p(s(T, v),v) = p(T, v).

И получаем другую пару уравнений состояния:

T = T(s, v) и p = p(T, v). (2.15.2)

Чисто исторически получилось так, что одно из этих уравнений состояния появилось на свет задолго до появления понятия энтропии и включает в свой состав легко измеряемые в опытах параметры p, v, T, формализуемые в уравнение p = p(T, v)

Вначале уравнение состояния идеального газа было получено экспериментально для условий с небольшими давлениями и температурами. В дальнейшем это уравнение было получено строго на основании молекулярно-кинетической теории газов.

Для 1 кг вещества уравнение состояния идеального газа p = p(T, v) имеет вид:

Для произвольного количества вещества:

Если в ряду произвольных количеств вещества выбирается молярное количество, то:

В этих 3х уравнениях p, н/м2, v, м3/кг, T, К – параметры состояния, Rу = 8314/μ Дж/кгК, R = 8314 Дж/кмольК – универсальная газовая постоянная, V – геометрический объем, который занимает вещество, м3, V΄ — его молярный объем нм3/кмоль, m – масса, кг, n – кмоль количество вещества, μ – мольная масса вещества, кг/кмоль.

Условие критерия стабильности (см. первую лекцию), который определяет принцип достоверности построения любого уравнения состояния, выполняется для pv = RуT:

p = RуT/v → (∂(-p)/∂v)T = RуT/v2 ≥ 0.

Еще раз вернемся к основному уравнению термодинамики:

dq = du + pdv → cxdT = cvdT + pdv и

рассмотрим частный случай: рабочее тело находится в состоянии идеального газа и совершается процесс х = p = const. Тогда из предыдущего уравнения следует, что

cp = cv + p(∂v/∂T)p и pv = RуT → v = (R у/p)T → (∂v/∂T)p = Rу/p.

cp = cv + Rу, и, конечно, cp > cv. (2.17)

Соотношение между теплоемкостями (2.17) в термодинамике носит название закона Майера. Из него следует, что на практике достаточно определить только одну теплоемкость cp или сv, чтобы сразу найти другую. И не будем забывать, что закон Майера справедлив только для идеального газа. Для реальных веществ с другими уравнениями состояния можно лишь говорить, что cp > cv.

Замечание. Уравнение Майера справедливо не только для истинных теплоемкостей, но и для средних. Дело в том, что операция усреднения (2.10) в (2.17) постоянной величины Rу дает в результате саму постоянную.

Как ясно из выведенных уравнений (2.13) и (2.14), внутренняя энергия и энтальпия зависят от свойств веществ. Действительно, первое слагаемое включает теплоемкость в явном виде, а во втором слагаемом она же входит в неявном виде как u = u(cv, T). Одновременно, свойства веществ отражаются уравнениями состояния u = u(s, v) и h = h(s, v). Следовательно, оценку роли u и h и их связи с поведением рабочих тел можно установить только, если известны уравнения состояния конкретного вещества (рабочего тела).

3.2. Внутренняя энергия идеального газа (свойства и расчет).

Из определения идеального газа следует, что внутренняя энергия (определение см. в лекции 1) идеального газа является просто кинетической энергией хаотического поступательного движения молекул газа. Потенциальная энергия взаимного расположения молекул в геометрическом пространстве, вращательная и колебательная энергия молекул идеального газа пренебрежимо малы по сравнению с кинетической энергией поступательного движения. Именно это обстоятельство позволило Больцману корректно провести усреднение кинетической энергии по множеству всех молекул и получить знаменитую формулу, известную из курса физики:

где k – постоянная Больцмана, Т – термодинамическая температура, u – средняя по множеству всех молекул кинетическая энергия.

Выражение (2.18) по существу показывает, что внутренняя энергия идеального газа является функцией только температуры и что изменение внутренней энергии Δu определяется только изменением температуры:

Здесь вместо точки в выражении частной производной можно подставить любой параметр состояния (конечно, кроме Т).

Отсюда сразу следует, что для идеального газа (см.(2.13) и (2.14)) расчет изменения внутренней энергии и энтальпии существенно упрощается, т. к. (∂u/∂v)T = 0 и (∂h/∂p) = 0 и

du = cvdT и dh = cpdT → Δu =(t2 – t1); Δh =(t2 – t1); (2.19)

И такой способ расчета изменений функций состояния справедлив для любых процессов с идеальным газом.

Можно также предложить другой способ расчета изменения функций состояния, если имеется в наличии диаграмма p – v или T – s для какого-то вещества в идеальном состоянии. Например, рассмотрим диаграмму T – s и процесс 1 – 2 на рис. 2.7.

Рис 2.7. Графический способ расчета изменения

внутренней энергии и энтальпии для идеального газа в процессе 1 – 2.

Точки 1 и 2 характеризуют два состояния с температурами Т1 и Т2 (на рис 2.7 показаны две соответствующие изотермы). Изменение энтальпии Δh определяется (см.(2.5)):

, (2.20)

и для функций состояния Δh не зависит от траектории процесса, а зависит только от температуры в начальном и конечном состоянии (изотермы Т1 и Т2). Глядя на (2.20), видно, что по диаграмме T – s нельзя найти определенный интеграл от vdp. Тогда расчет Δh будем вести не по реальной кривой 1 -2 на рис 3.1, а по изобаре p = const (dp = 0 и vdp = 0) и второй интеграл станет нулевым.

Строим изобару p = const на диаграмме, тогда площадь под изобарой в нужном температурном интервале Т1 и Т2 и будет численно равна изменению энтальпии Δh.

(2.21)

Строим изохору v = const, и площадь под ней в тех же температурных пределах будет численно равна изменению внутренней энергии в процессе 1 – 2.

Замечание. Расположение изохоры или изобары на плоскости с координатами T – s правее или левее относительно процесса 1 – 2 здесь не существенно: площадь под кривыми неизменна.

Также просто найти изменение функций состояния в любом процессе с идеальным газом, если он изображен на диаграмме с координатами p – v. Предлагаем студентам самим проделать эту процедуру в качестве тренировки.

Замечание. Такая простота и легкость расчета изменения функций состояния в любом процессе обусловлена двумя обстоятельствами:

1. Зависимостью внутренней энергии идеального газа только от температуры.

2. Независимостью приращения функций состояния от траектории процесса, а, следовательно, возможностью выбора удобной для интегрирования траектории в интервале лишь температур начала и конца процесса.

3.3. Свойства веществ и расчет изменения энтропии.

Изменение энтропии в каком-то процессе и для какого-то вещества будем рассчитывать стандартным путем:

Дифференциал энтропии явно содержится в (2.1) и (2.5):

du = Tds – pdv и dh = Tds + vdp. (2.1) и (2.5)

Обратимся снова к основным уравнениям (2.13) и (2.14), которые справедливы для любых веществ, например:

du = cvdT + (∂u/∂v)Tdv. (2.13)

Чтобы получить выражение для (∂u/∂v)T, воспользуемся (2.1): du = Tds – pdv. Разделим обе части этого уравнения на dv и потребуем неизменности температуры процесса. Получаем:

Исключим здесь производную (∂s/∂v)T с помощью одного из дифференциальных соотношений, которые мы просили студентов получить для тренировки:

(∂s/∂v)T = (∂p/∂T)v. Получаем:

Подставим (2.22) в (2.13), получаем

du = cvdT + [T(∂p/∂T)v – p]dv. (2.23)

Из (2.1) следует, что

du = Tds – pdv → Tds = du + pdv.

Подставим (2.23) в последнее выражение:

Tds = cvdT + T(∂p/∂T)vdv → ds = cvdT / T + (∂p/∂T)vdv (2.24)

Процедуру, которую мы только что проделали с (2.1), можно провести с (2.15), только придется воспользоваться другим дифференциальным соотношением, и получим еще одну расчетную формулу для дифференциала энтропии (предлагаем студентам поделать это самостоятельно):

ds = cpdT / T – (∂v/∂T)pdp. (2.25)

Теперь осталось проинтегрировать (2.24) или (2.25), если известны зависимости сv = f(T, p), cp = f(T, v) и уравнение состояния рабочего тела F(p, v,T) = 0. Отметим, что связи (2.24) и (2.25) справедливы для любого процесса с любым рабочим веществом.

Для идеального газа pv = RуT, cv = cv(T), cp = cp(T). Тогда, пользуясь понятием средней теплоемкости (2.10) и интегрируя ds, получаем расчетные формулы для изменения энтропии в любом процессе с идеальным газом:

Δs = cv|t1t2ln (T2/T1) + Rуln(v2/v1) или Δs = cp|t1t2ln(T2/T1) – Rуln(p2/p1), Дж/кгК. (2.26)

Формулы (2.26) можно чуть видоизменить, если воспользоваться уравнением состояния идеального газа:

T2/T1 = p2/p1 * v2/v1 → Δs = cp|t1t2 ln(v2/v1) + cv|t1t2 ln(p2/p

Эти три соотношения (2.26) и (2.27) исчерпывают связь изменения энтропии с параметрами состояния p, v, T для идеального газа в любом процессе.

4. Расчет количества работы.

«Работа – это изменение формы энергии, рассматриваемая с количественной стороны» — согласно формулировке Энгельса, данной еще в Х1Х веке. Для термодинамики это определение имеет двойное содержание: во-первых, нас будет интересовать количество работы или адекватная ей разность энергий рабочего тела, а, во-вторых, работа всегда связана с «движением», т. е. с упорядоченным перемещением вещества рабочего тела, которое взаимодействует с окружающей его средой.

Для теории, т. е. в нашем случае для термодинамики, существенна скорость взаимодействия, а она в математической терминологии предполагается бесконечно малой; также изменяются и параметры состояния. Подобные процессы («изменения состояния») уже названы (см. лекцию 1) равновесными или квазистатическими (мнимостатическими). В них в каждое мгновение перемены состояния существует равновесие между движущими силами (потенциалами) рабочего тела и окружающей среды и поэтому мы записываем dT, dp, du и т. д.

Естественно, что в подавляющем числе случаев превращения веществ, происходящих в природе и в промышленной практике, не равновесны, и поэтому необратимы в термодинамическом смысле, т. е. нельзя вернуть рабочее тело в первоначальное состояние без дополнительной затраты энергии от окружающей среды (т. е. без компенсации). Поэтому аппарат термодинамики (термостатики) в полной мере и в строгой форме к анализу действительных процессов не применим. Все же анализ подобного рода часто дает примерно верное отражение действительных изменений. Когда же глубина необратимости невелика, действительные изменения отражаются в равновесных (квазистатических) процессах достаточно точно

Задача расчета работы встречалась еще в школьном курсе физики, например, при расчете работы растяжения пружины или при движении груза по плоскости с трением. Для линейного перемещения работа W рассчитывается как

,

где F – сила растяжения пружины, l – перемещение свободного конца пружины. Для объемной деформации (раздувание резинового шара и промышленного газгольдера или сжатие газа в компрессоре) работа равна