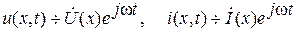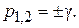Телеграфные уравнения однородной длинной линий
ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Общие сведения
Цепями с распределенными параметрами называются идеализированные электрические цепи, процессы в которых описываются дифференциальными уравнениями в частных производных. Это связано с тем, что если длина волны λ электромагнитных колебаний соизмерима с размерами цепи l, то токи и напряжения в этой одномерной цепи являются функциями двух переменных – времени t и координаты x – u(t, x), i(t, x).
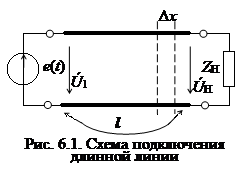
Задача анализа цепей с распределенными параметрами обычно сводится к определению законов (характера) изменения токов и напряжений вдоль цепи и к исследованию частотных и временных характеристик цепи. С этой целью следует рассмотреть электрическую модель отрезка линии малой длины Δx = dx. Эта модель с достаточной точностью исследования может быть представлена электрической цепью с сосредоточенными параметрами (рис. 6.2). Всю линию можно представить как цепи с бесконечно большим числом малых по величине пассивных элементов, распределенных равномерно по ее длине.
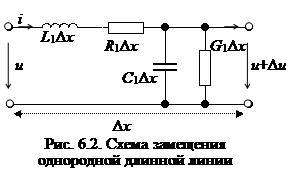
При прохождении тока вокруг проводника образуется внешнее магнитное поле, которое можно моделировать индуктивностью L0. Она препятствует прохождению тока. Вместе с этим проводник обладает сопротивлением материала R0. Следовательно, эти элементы должны быть соединены последовательно.
Проводники объединены конструктивно диэлектриком, который обладает конечной резистивной проводимостью G0. Между проводниками линии создается разность потенциалов. Следовательно, вокруг проводников существует электрическое поле, накопление которого моделируется емкостью С0.
Элементы L0, C0, R0, G0 называются параметрами линии (отрезка линии). Однако каждый отрезок линии имеет конечную длину Dx, поэтому вводятся понятия погонных параметров:
Телеграфные уравнения однородной длинной линий
Электрические процессы в цепях с распределенными параметрами описываются дифференциальными уравнениями в частных производных. Действительно, ток i = i(x, t) и напряжение u = u(x, t) рассматриваемой цепи являются функциями времени t и координаты x.
Составим на основе законов Кирхгофа дифференциальные уравнения для мгновенных напряжений и токов на отрезке линии длиной Δx по эквивалентной схеме на рис. 6.2.
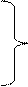
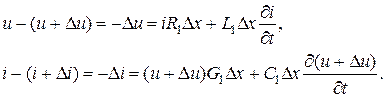
Разделив обе части уравнений (6.1) на Δx, переходя к пределу при Δx → 0 и пренебрегая величинами второго порядка малости, получим дифференциальные уравнения линии
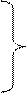
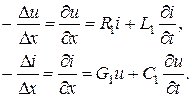
Эти уравнения в частных производных называются телеграфными, так как впервые были получены для линии телеграфной связи.
Пусть к началу линии подключен генератор гармонических колебаний e(t) = Emcos(ωt + φ0), а к концу линии – сопротивление нагрузки ZH (рис. 6.1). Будем считать, что в линии имеет место режим установившихся гармонических колебаний.
Используя символический метод анализа гармонических колебаний, в котором
преобразуем уравнения (6.2) для мгновенных комплексных значений напряжения и тока
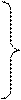
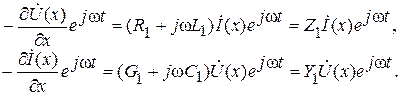

Заменим в (6.3) частную производную на полную, т.к. 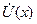
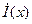
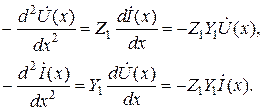
Введем обозначение 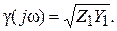
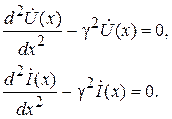
Уравнения (6.5) называются телеграфными уравнения однородной линии в комплексной форме. Они являются однородными, 2-го порядка, линейными (т.к. Z1 и Y1 не зависят от x).
Корни характеристического уравнения p 2 – γ 2 = 0 системы (6.5) равны
Общее решение первого уравнения системы (6.5) для напряжения в произвольной точке x линии ищем в виде
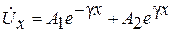
Из первого уравнения системы (6.3)
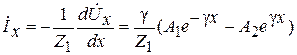
Введя еще одно обозначение
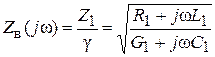
запишем решение для тока в точке x в форме
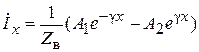
Постоянные интегрирования A1 и A2 можно найти из начальных условий:
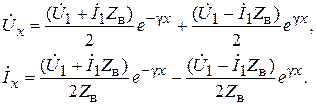
Выражения (6.11) называют уравнениями передачи длинной линии.Они позволяют рассмотреть распределение напряжений и токов в однородной длинной линии в произвольной точке x.
Дата добавления: 2016-11-02 ; просмотров: 4552 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Длинная линия
Длинная линия
Содержание
- 1 Дифференциальные уравнения длинной линии
- 1.1 Погонные параметры 1.2 Эквивалентная схема участка длинной линии 1.3 Телеграфные уравнения 1.4 Условие регулярности линии 1.5 Однородные волновые уравнения длинной линии 1.6 Распределение поля падающей волны
2 Комплексный коэффициент отражения по напряжению 3 Коэффициенты бегущей и стоячей волны 4 Входное сопротивление длинной линии 5 Режимы работы длинной линии
- 5.1 Режим бегущей волны 5.2 Режим стоячей волны 5.3 Режим смешанных волн
6 Линия без потерь
- 6.1 Разомкнутая линия 6.2 Замкнутая линия 6.3 Ёмкостная нагрузка 6.4 Индуктивная нагрузка 6.5 Активная нагрузка 6.6 Комплексная нагрузка
7 КПД линии с потерями 8 Пределы применимости теории длинной линии 9 См. также 10 Примечания
Длинная линия — регулярная линия передачи[1], длина которой превышает длину волны (λ) колебаний, распространяющихся в линии.
Характерной особенностью длинных линий является проявление интерференции двух волн, распространяющихся навстречу друг другу. Одна из этих волн создается генератором электромагнитных колебаний, подключенным к линии, и называется падающей. Другая волна может возникать из-за отражения падающей волны от нагрузки, подключенной к противоположному концу линии, и называется отраженной. Отраженная волна распространяется в направлении, обратном падающей волне. Все разнообразие процессов, происходящих в длинной линии, определяется амплитудно-фазовыми соотношениями между падающей и отраженной волнами.
Дифференциальные уравнения длинной линии
Рассмотрим двухпроводную длинную линию, представленную на рисунке 1. На рисунке обозначено: ZН = RН + iXН — комплексное сопротивление нагрузки; z — продольная координата линии, отсчитываемая от места подключения нагрузки.
Погонные параметры
Рис.1 — К выводу дифференциальных уравнений длинной линии
Из электродинамики известно, что линия передачи может быть охарактеризована ее погонными параметрами:
- R1 — погонное сопротивление, Ом/м; G1 — погонная проводимость, 1/Ом м; L1 — погонная индуктивность Гн/м; C1 — погонная ёмкость Ф/м;
Погонные сопротивление R1 и проводимость G1 зависят от проводимости материала проводов и качества диэлектрика, окружающего эти провода, соответственно. Чем меньше тепловые потери в металле проводов[2] и в диэлектрике, тем меньше соответственно, R1[3] и G1[4]. Погонные индуктивность L1 и емкость C1 определяются формой и размерами поперечного сечения проводов, а также расстоянием между ними.
Эквивалентная схема участка длинной линии
Рис.2 — Эквивалентная схема участка длинной линии
Выделим из линии элементарный участок бесконечно малой длины dz и рассмотрим его эквивалентную схему, покзанную на рисунке 2. На этой схеме стрелками обозначены направления отсчета напряжения U и тока I в линии; dU и dI — приращения напряжения и тока в линии на элементе длины dz. Значения параметров схемы определяются соотношениями:
Используя эквивалентную схему, запишем выражения для приращений напряжения и тока:
Подставляя сюда значения параметров схемы из (1), получаем:

где Z1 = R1 + iωL1, Y1 = G1 + iωC1 — погонные комплексные сопротивление и проводимость линии. Из последних соотношений находим дифференциальные уравнения линии:
Телеграфные уравнения
Основная статья: Телеграфное уравнение
Эти соотношения называются телеграфными уравнениями длинной линии. Они определяют связь между током и напряжением в любом сечении линии. Решим телеграфные уравнения относительно напряжения и тока. Для этого продифференцируем их по z:
При этом учтем, что:
Условие регулярности линии
Данные соотношения являются математическим определением регулярности длинной линии. Смысл соотношения (4) состоит в неизменности вдоль линии ее погонных параметров.
Подставляя в (3) значения производных напряжения и тока из (2), после преобразований получаем:
Однородные волновые уравнения длинной линии

где γ — коэффициент распространения волны в линии: 
Соотношения (5) называются однородными волновыми уравнениями длинной линии. Их решения известны и могут быть записаны в виде:

где AU, BU и AI, BI — коэффициенты, имеющие единицы измерения напряжения и тока соответственно, смысл которых будет ясен ниже.
Решения волновых уравнений в виде (3.6) имеют весьма характерный вид: первое слагаемое в этих решениях представляет собой падающую волну напряжения или тока, распространяющуюся от генератора к нагрузке, второе слагаемое — отраженную волну, распространяющуюся от нагрузки к генератору. Таким образом, коэффициенты AU, AI представляют собой комплексные амплитуды падающих волн напряжения и тока соответственно, а коэффициенты BU, BI — комплексные амплитуды отраженных волн напряжения и тока соответственно. Так как часть мощности, передаваемой по линии, может поглощаться в нагрузке, то амплитуды отраженных волн не должны превышать амплитуды падающих:
Направление распространения волн в (6) определяется знаком в показателях степени экспонент: плюс — волна распространяется в отрицательном направлении оси z; минус — в положительном направлении оси z (см. рис. 1).Так, например, для падающих волн напряжения и тока можно записать:

Коэффициент распространения волны в линии γ в общем случае является комплексной величиной и может быть представлен в виде:

где α — коэффициент затухания волны[5] в линии; β — коэффициент фазы[6]. Тогда соотношение (7) можно переписать в виде:

Так как при распространении падающей волны на длину волны в линии λЛ фаза волны изменяется на 2π , то коэффициент фазы можно связать с длиной волны λЛ соотношением

При этом фазовая скорость волны в линии VФ определяется через коэффициент фазы:

Определим коэффициенты A и B , входящие в решения (6) волновых уравнений, через значения напряжения UН и тока IН на нагрузке. Это является оправданным, так как напряжение и ток на нагрузке практически всегда можно измерить с помощью измерительных приборов. Воспользуемся первым из телеграфных уравнений (2) и подставим в него напряжение и ток из (6). Тогда получим:
Сравнив коэффициенты при экспонентах с одинаковыми показателями степеней, получим:

где 
Перепишем (6) с учетом (12):

Для определения коэффициентов A и B в этих уравнениях воспользуемся условиями в конце линии z = 0:

Тогда из (13) при z = 0 найдем

Подставив полученные значения коэффициентов из (14) в (13), после преобразований получим:

При выводе (15) учтены определения гиперболических синуса и косинуса[8].
Соотношения для напряжения и тока (15) так же, как и (6), являются решениями однородных волновых уравнений. Их отличие состоит в том, что напряжение и ток в линии в соотношении (6) определены через амплитуды падающей и отраженной волн, а в (15) — через напряжение и ток на нагрузке.
Рассмотрим простейший случай, когда напряжение и ток в линии определяются только падающей волной, а отраженная волна отсутствует[9]. Тогда в (6) следует положить BU = 0, BI = 0:

Распределение поля падающей волны
Рис.3. Эпюры напряжений падающей волны в длинной линии. а) амплитуда; б) фаза
На рис.3. представлены эпюры изменения амплитуды |U| и фазы φU апряжения вдоль линии. Эпюры изменения амплитуды и фазы тока имеют такой же вид. Из рассмотрения эпюр следует, что при отсутствии в линии потерь (α[5] = 0) амплитуда напряжения в любом сечении линии остается одной и той же. При наличии потерь в линии (α[5] > 0) часть переносимой мощности преобразуется в тепло (нагревание проводов линии и окружающего их диэлектрика). По этой причине амплитуда напряжения падающей волны экспоненциально убывает в направлении распространения.
Фаза напряжения падающей волны φU = β z изменяется по линейному закону и уменьшается по мере удаления от генератора.
Рассмотрим изменение амплитуды и фазы, например, напряжения при наличии падающей и отраженной волн. Для упрощения положим, что потери в линии отсутствуют, то есть α[5] = 0. Тогда напряжение в линии можно представить в виде:

где Γ = BU / AU — комплексный коэффициент отражения по напряжению.
Комплексный коэффициент отражения по напряжению
Характеризует степень согласования линии передачи с нагрузкой. Модуль коэффициента отражения изменяется в пределах:
- | Г | = 0, если отражения от нагрузки отсутствуют и BU = 0[9]; | Г | = 1, если волна полностью отражается от нагрузки, то есть | AU | = | BU | ;
Соотношение (16) представляет собой сумму падающей и отраженной волн.
Рис.4. Векторная диаграмма напряжений в линии с отраженной волной
Отобразим напряжение на комплексной плоскости в виде векторной диаграммы, каждый из векторов которой определяет падающую, отраженную волны и результирующее напряжение (рис. 4). Из диаграммы видно, что существуют такие поперечные сечения линии, в которых падающая и отраженная волны складываются в фазе. Напряжение в этих сечениях достигает максимума, величина которого равна сумме амплитуд падающей и отраженной волн:

Кроме того, существуют такие поперечные сечения линии, в которых падающая и отраженная волны складываются в противофазе. При этом напряжение достигает минимума:

Если линия нагружена на сопротивление, для которого |Г| = 1 , т. е. амплитуда падающей и отраженной волн равны |BU| = |AU|, то в этом случае Umax = 2|AU|, а Umin = 0.
Рис.5. Эпюры распределения напряжения вдоль линии с отражённой волной. а) Модуль напряжения; б) фаза напряжения.
Напряжение в такой линии изменяется от нуля до удвоенной амплитуды падающей волны. На рис. 5 представлены эпюры изменения амплитуды и фазы напряжения вдоль линии при наличии отраженной волны.
Коэффициенты бегущей и стоячей волны
По эпюре напряжения судят о степени согласования линии с нагрузкой. Для этого вводятся понятия коэффициента бегущей волны — kБВ и коэффициента стоячей волны kСВ:
Эти коэффициенты, судя по определению, изменяются в пределах:


На практике наиболее часто используется понятие коэффициента стоячей волны, так как современные измерительные приборы (панорамные измерители kСВ) на индикаторных устройствах отображают изменение именно этой величины в определенной полосе частот.
Входное сопротивление длинной линии
Входное сопротивление линии — является важной характеристикой, которое определяется в каждом сечении линии как отношение напряжения к току в этом сечении:
Так как напряжение и ток в линии изменяются от сечения к сечению, то и входное сопротивление линии изменяется относительно ее продольной координаты z. При этом говорят о трансформирующих свойствах линии, а саму линию рассматривают как трансформатор сопротивлений. Подробнее свойство линии трансформировать сопротивления будет рассмотрено ниже.
Режимы работы длинной линии
Различают три режима работы линии:
режим бегущей волны; [10] режим стоячей волны; [10] режим смешанных волн.
Режим бегущей волны
Режим бегущей волны характеризуется наличием только падающей волны, распространяющейся от генератора к нагрузке. Отраженная волна отсутствует. Мощность, переносимая падающей волной, полностью выделяется в нагрузке. В этом режиме BU = 0, | Г | = 0, kбв =kсв = 1[10].
Режим стоячей волны
Режим стоячей волны характеризуется тем, что амплитуда отраженной волны равна амплитуде падающей BU = AU т. е. энергия падающей волны полностью отражается от нагрузки и возвращается обратно в генератор. В этом режиме, | Г | = 1, kсв = 
Режим смешанных волн
В режиме смешанных волн амплитуда отраженной волны удовлетворяет условию 0 W Сопротивление нагрузки меньше волнового сопротивления линии RН
Телеграфные уравнения, волновое уравнение
| Рассмотрим распределенную колебательную систему на примере двухпроводной линии. Если расстояние между проводниками мало в сравнении с длиной линии l и длиной волны l, передаваемых колебаний в ней, то векторы магнитного и электрического поля лежат в плоскости, перпендикулярной направлению линии, в этой плоскости удовлетворяют уравнению Лапласа и могут считаться потенциальными. Поэтому для малых участков | 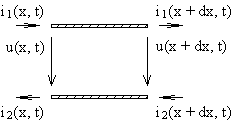 Рис. 79. Двухпроводная линия. Рис. 79. Двухпроводная линия. |
линии dx (рис. 79) можно ввести понятия потенциала, тока, распределенных ёмкостей и индуктивностей. Если система не излучает и не взаимодействует с другими проводниками, то в каждом сечении линии токи в обоих проводниках равны по величине и противоположны по направлению: i1(x, t) = —i2(x, t) = i(x, t).
Рассмотрим бесконечно малый элемент dx длины линии, обладающей индуктивностью L и ёмкостью C на единицу длины линии. Для участка dx линии можно записать уравнения Кирхгофа:
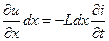
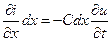
откуда легко получаются телеграфные уравнения:
 , , 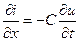 . . | (9.1) |
Из уравнений (9.1) легко получаются и волновые уравнения для тока и напряжения:
 , , 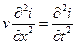 , , | (9.2) |
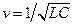 — фазовая скорость. — фазовая скорость. | (9.3) |
Волновое уравнение можно получить также, если рассматривать, например, распределённую электрическую систему как предельный случай одномерной цепочки, составленной из сосредоточенных индуктивностей и емкостей. Если увеличивать число ячеек на единицу длины цепочки, сохраняя постоянной общую индуктивность и ёмкость, то в пределе система уравнений для цепочки (8.32) перейдёт в волновое уравнение (9.2). Координата x соответствует изменяющемуся номеру ячейки.
Частным решением волнового уравнения (9.2) являются любые функции вида
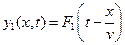
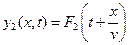
соответственно полное решение имеет вид:
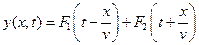 . . | (9.4) |
Первое слагаемое описывает волну, которая распространяется, не меняя своей формы, в направлении возрастания x, а второе — волну, распространяющуюся с той же скоростью в сторону убывания x. Для процессов, синусоидальных во времени, решение (9.4) принимает форму
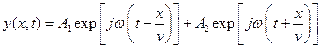
Здесь величина w(t ± x/v) называется фазой волны, а величина k = w/v — волновым числом. Волновое число характеризует пространственную периодичность волнового процесса, т. е. y(x + nl, t) = y(x, t), и связана с длиной волны соотношением: k = 2p/l.
Для токов и напряжений в линии решение уравнения (9.4) имеет вид:
 | (9.5) |
Подставляя эти выражения в телеграфное уравнение (9.1), получим связь между коэффициентами:


где 
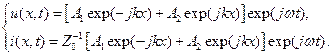 | (9.6) |
Погонные индуктивность и ёмкость линии определяются её геометрией. Для двухпроводной линии в системе СГС получаем
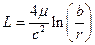 , , 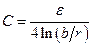 , , | (9.7) |
где r — радиус проводов, b — расстояние между ними.
Учитывая два последних соотношения, получим для волнового сопротивления следующее выражение:

Для коаксиальной линии имеем
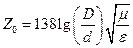
где D и d — диаметры внешнего и внутреннего проводников.
Подставляя погонные L и C в (9.3), получим, что фазовая скорость волны в линии равна
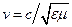 . . | (9.8) |
Для двухпроводной линии с погонным сопротивлением проводников R и погонной утечкой G между ними телеграфные уравнения (9.1) принимают вид:
 , ,  . . | (9.9) |
Для гармонического во времени процесса уравнения (9.9) запишутся следующим образом:
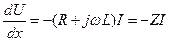
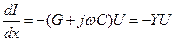
где Z и Y — комплексные последовательное сопротивление и параллельная утечка, U и I — комплексные амплитуды напряжения и тока. Из этих двух телеграфных уравнений получим уравнение для U
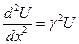
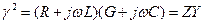
Его решение имеет вид:

причём постоянная распространения g в данном случае является комплексной величиной. Представим её так:
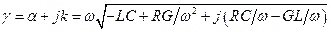
Тогда мы вправе записать

Теперь и падающая и отражённая волны содержат множитель, характеризующий затухание. Поскольку и мнимая, и действительная части g являются нелинейными функциями частоты, то и фазовая скорость волны v = w/k зависит от частоты. Это явление называется дисперсией. Волновое сопротивление линии с потерями тоже комплекснозначная функция частоты
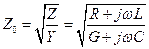
http://pandia.ru/text/78/209/31613.php
http://megalektsii.ru/s31341t3.html