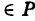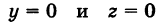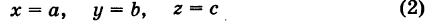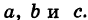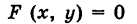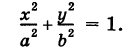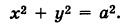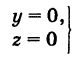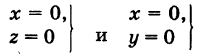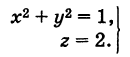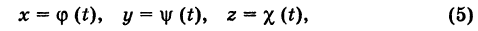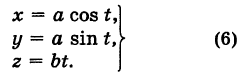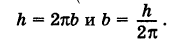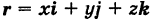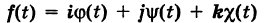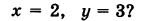Тело по заданным уравнениям поверхностей

Уравнения поверхности и линии в пространстве с примерами решения

Содержание:

Уравнения поверхности и линии в пространстве

Определение: Уравнение м поверхности в пространстве Oxyz называется такое уравнение между переменными х, у у z, которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности. То есть если

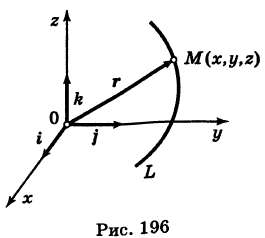
— уравнение поверхности Р (рис. 189), то при М(х, у, z)

Таким образом, уравнение (1) выполнено тогда и только тогда, когда точка М(х, у, z) принадлежит данной поверхности. Координаты произвольной точки поверхности называются текущими координатами точки. Поэтому составить уравнение поверхности — это значит найти связь между текущими координатами ее точек.

Пример (уравнения координатных плоскостей):

Каждая точка М(х, у, z), лежащая на координатной плоскости Oyz, имеет абсциссу х = 0; обратно, если для какой-нибудь точки М(х, у, z) абсцисса ее х = 0, то эта точка расположена на плоскости Oyz. Следовательно,

— уравнение координатной плоскости Oyz. Аналогично,

— соответственно уравнения координатных плоскостей Oxz и Оху.

Формула обозначает, что точка М принадлежит Р. Формула обозначает, что точка N не принадлежит Р.

В более общем случае

— уравнения трех плоскостей, перпендикулярных соответствующим координатным осям Ох, Оу, Ог и отсекающих на них отрезки, численно равные

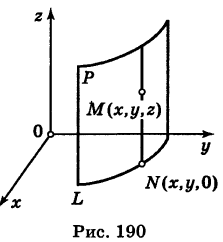
Теорема: Уравнение цилиндрической поверхности, образующие которой параллельны координатной оси, не содержит текущей координаты, одноименной с этой координатной осью, и обратно.

Доказательство: Пусть, например, цилиндрическая поверхность Р образована перемещением прямой 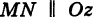(образующая) вдоль заданной линии L, лежащей в плоскости Оху (направляющая) (рис. 190).

Обозначим через М(х, у, z) точку поверхности Р с текущими координатами х, у и z. Образующая MN, проходящая через точку М, пересекает направляющую, очевидно, в точке N(x, у, 0).

— уравнение направляющей L в координатной плоскости Оху. Этому уравнению удовлетворяют координаты точки N. Так как точка М поверхности Р имеет ту же самую абсциссу хиту же самую ординату у, что и точка N, а переменная г в уравнение (3) не входит, то координаты точки М также удовлетворяют уравнению (3). Таким образом, координаты любой точки М(х, у, z) поверхности Р удовлетворяют уравнению (3). Обратно, если координаты какой-нибудь точки М(х, у, z) удовлетворяют уравнению (3), то эта точка расположена на прямой MN || Оz такой, что ее след на плоскости Оху, точка N(x, у, 0), лежит на линии L, а значит, точка М принадлежит цилиндрической поверхности Р. Следовательно,

является уравнением цилиндрической поверхности в пространстве Oxyz, причем в этом уравнении отсутствует координата z.

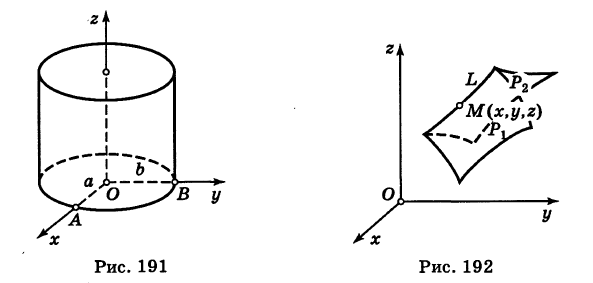
Пример (уравнение эллиптического цилиндра):

Эллиптический цилиндр, в основании которого лежит эллипс с полуосями а и b, а осью служит ось Оz (рис. 191), на основании предыдущей теоремы имеет уравнение

В частности, при а = b получаем уравнение кругового цилиндра

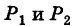
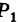
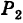
Линию L в пространстве можно задать как пересечение двух данных поверхностей (рис. 192). Точка , лежащая на линии L, принадлежит как поверхности так и поверхности , и, следовательно, координаты этой точки удовлетворяют уравнениям обеих поверхностей.

Поэтому под уравнениями линии в пространстве понимается совокупность двух уравнений:

являющихся уравнениями поверхностей, определяющих данную линию.

Не нужно думать, что для нахождения уравнений линий систему (4) следует «решить». Этого, вообще говоря, нельзя сделать, так как число уравнений системы (4) меньше числа неизвестных. Точный смысл, который придается равенствам (4), следующий: линии L принадлежат те и только те точки , координаты которых удовлетворяют обоим уравнениям системы (4).

Заметим, что данную линию можно по-разному задавать как пересечение поверхностей. Поэтому линии в пространстве соответствует бесчисленное множество равносильных между собой систем уравнений.

Определение: Уравнениями линии в пространстве называется такая пара уравнений между переменными , которой удовлетворяют координаты каждой точки, лежащей на данной линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.

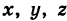
Пример (уравнения координатных осей):

Ось Ох можно, рассматривать как пересечение координатных плоскостей Оху и Oxz. Поэтому

— уравнения оси Ох. Аналогично,

— уравнения осей Оу и Oz соответственно.

Пример:

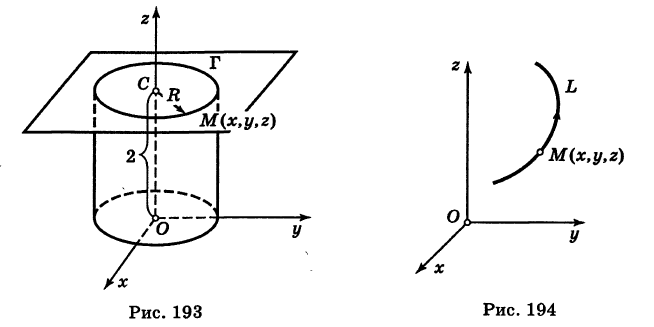
Написать уравнения окружности Г радиуса R = 1, центр которой находится в точке С(0, 0, 2) и плоскость которой параллельна координатной плоскости Оху (рис. 193).

Решение:

Окружность Г можно рассматривать как пересечение кругового цилиндра радиуса 1 с осью Oz и горизонтальной плоскости, расположенной выше координатной плоскости Оху на две единицы. Поэтому уравнения данной окружности есть

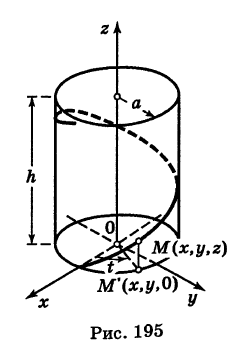
В механике линию L часто рассматривают как след движущейся точки (рис. 194). Пусть х, у, z — текущие координаты точки М линии L. Так как с течением времени точка М перемещается и ее координаты меняются, то они являются функциями времени t. Следовательно, имеем

где 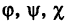— некоторые определенные функции. Обобщая уравнения (5), под t понимают вспомогательную переменную (параметр)> не обязательно время; поэтому уравнения (5) носят название параметрических уравнений линии в пространстве.

Исключая из уравнений (5) параметр t, мы получим два соотношения между текущими координатами х, у и z, которые представляют собой уравнения некоторых поверхностей, проходящих через данную линию.

Пример:

Написать уравнения винтовой линии радиуса а и шага 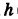(рис. 195).

Решение:

Пусть М (х, у, z) — текущая точка винтовой линии, М’ (х, у, 0) — ее проекция на плоскость Оху.

Приняв за параметр 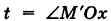и учитывая, что аппликата г винтовой линии растет пропорционально углу поворота t, будем иметь

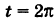
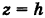
Для определения коэффициента пропорциональности b положим ; тогда . Следовательно,

Исключая параметр t из первого и второго, а также из первого и третьего уравнений (6), получаем

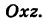
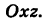
Следовательно, винтовая линия представляет собой пересечение кругового цилиндра с образующими, параллельными оси Oz, и цилиндрической поверхности с образующими, параллельными оси Оу, и имеющей своей направляющей косинусоиду, лежащую в плоскости . Из уравнений (6′) также вытекает, что проекция винтовой линии (6′) на координатную плоскость Оху есть окружность, а на координатную плоскость — косинусоида.

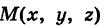
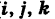
Текущую точку кривой L можно характеризовать ее радиусом-вектором («следящий радиус-вектор») (рис. 196)

( — орты). Тогда из (5) получаем векторное уравнение линии

— так называемая вектор-функция скалярного аргумента t.

В механике в качестве параметра t обычно берут время. В таком случае линию (7) называют траекторией точки М(х, у, z).

Множество всех точек М(х, у, г) пространства, координаты которых удовлетворяют данному уравнению (или системе уравнений), называется геометрическим образом (графиком) данного уравнения (или системы уравнений).

Пример:

Какой геометрический образ соответствует уравнению

Решение:

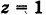
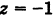
Из уравнения (8) получаем или . Следовательно, графиком уравнения (8) является пара плоскостей, параллельных координатной плоскости Оху и отстоящих от нее на расстояниях, равных единице (рис. 197).

Пример:

Какой геометрический образ соответствует паре уравнений

Решение:

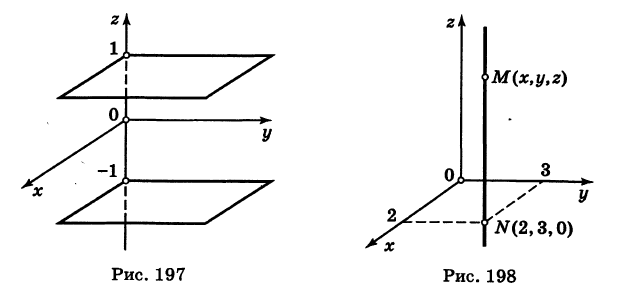
Искомый график представляет собой пересечение плоскостей х = 2 и у = 3 и, следовательно, является прямой линией, параллельной оси Oz и имеющей след N (2, 3, 0) на координатной плоскости Оху (рис. 198).

• Общее уравнение плоскости
• Угол между плоскостями
• Понятие о производной вектор-функции
• Криволинейные интегралы
• Прямоугольная система координат на плоскости и ее применение
• Линии второго порядка
• Полярные координаты
• Непрерывность функции

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Построение поверхности 3D

Результат

Примеры поверхностей

• Эллиптический параболоид
• Двухсторонний гиперболоид
• Мнимый эллипсоид
• Две параллельные плоскости
• Тригонометрические функции

Указанные выше примеры содержат также:

• квадратные корни sqrt(x),
  кубические корни cbrt(x)
• тригонометрические функции:
  синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
• показательные функции и экспоненты exp(x)
• обратные тригонометрические функции:
  арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x)
• натуральные логарифмы ln(x),
  десятичные логарифмы log(x)
• гиперболические функции:
  гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
• обратные гиперболические функции:
  asinh(x), acosh(x), atanh(x), actanh(x)
• число Пи pi
• комплексное число i

Правила ввода

Можно делать следующие операции

2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:

Вычисление объёмов

Вычисление объёмов

1. Услуги проектирования
2. Двойной интеграл
3. Вычисление объёмов

Вычисление объёмов

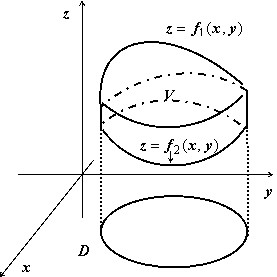
Объём тела, ограниченного сверху и снизу поверхностями $\mathbf < \textit < z >> =\mathbf < \textit < f >> _ < 1 >(\mathbf < \textit < x >> $,$\mathbf < \textit < y >> )$, $\mathbf < \textit < z >> =\mathbf < \textit < f >> _ < 2 >(\mathbf < \textit < x >> $,$\mathbf < \textit < y >> )$, $(x,y)\in D$, с боков — цилиндрической поверхностью с образующими, параллельными оси $\mathbf < \textit < Oz >> $, равен $v=\iint\limits_D < \left[ < f_1 (x,y)-f_2 (x,y) >\right]dxdy > $; эта формула очевидно следует из геометрического смысла двойного интеграла.

Основной вопрос, который надо решить — на какую координатную плоскость проектировать тело, чтобы выкладки были наиболее простыми.

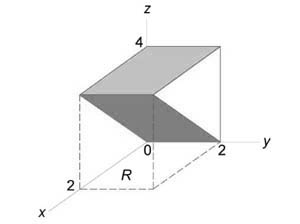
Найти объём тела $V:\left[ < \begin < l >y=0,\;z=0, \\ x+y+z=4,\; \\ 2x+z=4. \\ \end >\right.$

Решение:

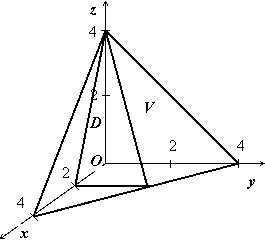
Тело изображено на рисунке. Перебором возможностей убеждаемся, что проще всего описать это тело, если отправляться от его проекции на ось $\mathbf < \textit < Oxz >> $:

$V:\left[ < \begin < l >(x,z)\in D, \\ 0\leqslant y\leqslant 4-x-z. \\ \end >\right.$

Область $\mathbf < \textit < D >> $ — треугольник, ограниченный прямыми $\mathbf < \textit < x >> $ = 0, $\mathbf < \textit < z >> $ = 0, 2$\mathbf < \textit < x >> +\mathbf < \textit < z >> $ = 4, поэтому

Найти объём области, ограниченной поверхностями $\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >+\mathbf < \textit < z >> ^ < 2 >=\mathbf < \textit < R >> ^ < 2 >$,

Решение:

Первая поверхность — сфера, вторая — цилиндрическая — с образующими, параллельными оси $\mathbf < \textit < Oz >> $ < в уравнении нет $\mathbf < \textit < z >> $ в явной форме). Построить в плоскости $\mathbf < \textit < Oxy >> $ кривую шестого порядка, заданную уравнением $(\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >)^ < 3 >=\mathbf < \textit < R >> ^ < 2 >(\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >)$, в декартовой системе координат невозможно, можно только сказать, что она симметрична относительно осей < чётные степени >и точка $\mathbf < \textit < О >> (0,0)$ принадлежит этой кривой. Пробуем перейти к полярным координатам. $r^6=R^2r^4(\cos ^4\varphi +\sin ^4\varphi );r^2=R^2((\cos ^2\varphi +\sin ^2\varphi )^2-2\cos ^2\varphi \sin ^2\varphi )=R^2(1-\frac < \sin ^22\varphi > < 2 >)=$

$=R^2(1-\frac < 1-\cos 4\varphi > < 4 >)=R^2\frac < 3+\cos 4\varphi > < 4 >;r=R\frac < \sqrt < 3+\cos 4\varphi >> < 2 >.$ Эту кривую построить уже можно. $r(\varphi )$ максимально, когда $\cos 4\varphi =1\;(\varphi =0,\frac < 2\pi > < 4 >=\frac < \pi > < 2 >,\frac < 4\pi > < 4 >=\pi ,\frac < 6\pi > < 4 >=\frac < 3\pi > < 2 >)$, минимально, когда

$\cos 4\varphi =-1\;(\varphi =\frac < \pi > < 4 >,\frac < 3\pi > < 4 >,\frac < 5\pi > < 4 >,\frac < 7\pi > < 4 >),$ и гладко меняется между этими пределами < точка $\mathbf < \textit < О >> (0,0)$ не принадлежит этой кривой, где мы её потеряли? > .

Найти объем тела в первом октанте, ограниченного плоскостями (y = 0,) (z = 0,) (z = x,) (z + x = 4.)

Решение:

Данное тело показано на рисунке.

Из рисунка видно, что основание (R) является квадратом. Для заданных (x, y) значение (z) изменяется от (z = x) до (z = 4 — x.) Тогда объем равен $ < V = \iint\limits_R < \left[ < \left( < 4 - x >\right) — x >\right]dxdy > > = < \int\limits_0^2 < \left[ < \int\limits_0^2 < \left( < 4 - 2x >\right)dy > >\right]dx > > = < \int\limits_0^2 < \left[ < \left. < \left( < 4y - 2xy >\right) >\right|_ < y = 0 >^2 >\right]dx > > = < \int\limits_0^2 < \left( < 8 - 4x >\right)dx > > = < \left. < \left( < 8x - 2 < x^2 >>\right) >\right|_0^2 > = < 16 - 8 = 8. >$

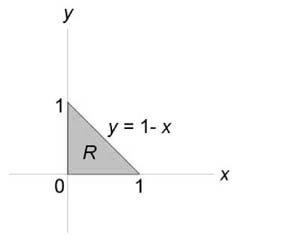
Описать тело, объем которого определяется интегралом (V = \int\limits_0^1 < dx >\int\limits_0^ < 1 - x > < \left( < < x^2 >+ < y^2 >>\right)dy > .)

Решение:

Данное тело расположено над треугольной областью (R,) ограниченной координатными осями (Ox,) (Oy) и прямой (y = 1 — x) ниже параболической поверхности (z = < x^2 >+ < y^2 >.) Объем тела равен $ < V = \int\limits_0^1 < dx >\int\limits_0^ < 1 - x > < \left( < < x^2 >+ < y^2 >>\right)dy > > = < \int\limits_0^1 < \left[ < \left. < \left( < < x^2 >y + \frac < < < y^3 >> > < 3 >>\right) >\right|_ < y = 0 >^ < 1 - x >>\right]dx > > = < \int\limits_0^1 < \left[ < < x^2 >\left( < 1 - x >\right) + \frac < < < < \left( < 1 - x >\right) > ^3 > > > < 3 >>\right]dx > > = \\ = < \int\limits_0^1 < \left( < < x^2 >— < x^3 >+ \frac < < 1 - 3x + 3 < x^2 >— < x^3 >> > < 3 >>\right)dx > > = < \int\limits_0^1 < \left( < 2 < x^2 >— \frac < < 4 < x^3 >> > < 3 >— x + \frac < 1 > < 3 >>\right)dx > > = < \left. < \left( < \frac < < 2 < x^3 >> > < 3 >— \frac < 4 > < 3 >\cdot \frac < < < x^4 >> > < 4 >— \frac < < < x^2 >> > < 2 >+ \frac < x > < 3 >>\right) >\right|_0^1 > = < \frac < 2 > < 3 >— \frac < 1 > < 3 >— \frac < 1 > < 2 >+ \frac < 1 > < 3 >= \frac < 1 > < 6 >. > $

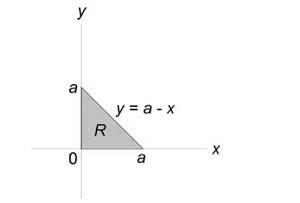
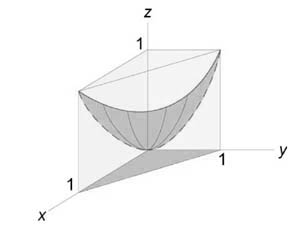
Вычислить объем тела, ограниченного поверхностями (z = xy,) (x + y = a,) (z = 0.)

Решение:

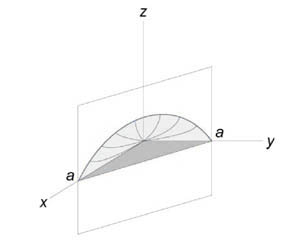
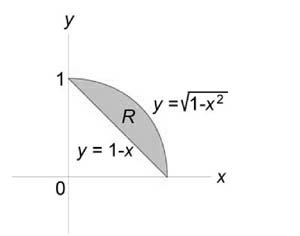
Найти объем тела, ограниченного поверхностями (z = 0,) (x + y = 1,) ( < x^2 >+ < y^2 >= 1,) (z = 1 — x.)

Решение:

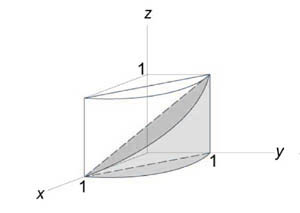
Как видно из рисунков, в области интегрирования (R) при (0 \le x \le 1) значения (y) изменяются от (1 — x) до (\sqrt < 1 - < x^2 >> .)

Вычислим второй интеграл ( < I_2 >= \int\limits_0^1 < x\sqrt < 1 - < x^2 >> dx > ,) используя замену переменной. Полагаем (1 — < x^2 >= w.) Тогда (-2xdx = dw) или (xdx = \large\frac < < - dw >> < 2 >\normalsize.) Находим, что (w = 1) при (x = 0) и, наоборот, (w = 0) при (x = 1.) Интеграл равен $ < < I_2 >= \int\limits_0^1 < x\sqrt < 1 - < x^2 >> dx > > = < \int\limits_1^0 < \sqrt w \left( < - \frac < < dw >> < 2 >>\right) > > = < - \frac < 1 > < 2 >\int\limits_1^0 < \sqrt w dw >> = < \frac < 1 > < 2 >\int\limits_0^1 < \sqrt w dw >> = < \frac < 1 > < 2 >\int\limits_0^1 < < w^ < \large\frac < 1 > < 2 >\normalsize > > dw > > = < \frac < 1 > < 2 >\left. < \left( < \frac < < 2 < w^ < \large\frac < 3 > < 2 >\normalsize > > > > < 3 >>\right) >\right|_0^1 = \frac < 1 > < 3 >. > $ Наконец, вычислим третий интеграл. $\require < cancel > < < I_3 >= \int\limits_0^1 < \left( < 1 - 2x + < x^2 >>\right)dx > > = < \left. < \left( < x - < x^2 >+ \frac < < < x^3 >> > < 3 >>\right) >\right|_0^1 > = < \cancel < 1 >— \cancel < 1 >+ \frac < 1 > < 3 >= \frac < 1 > < 3 >. > $ Таким образом, объем тела равен $ < V = < I_1 >— < I_2 >— < I_3 >> = < \frac < \pi > < 4 >— \frac < 1 > < 3 >— \frac < 1 > < 3 >= \frac < \pi > < 4 >— \frac < 2 > < 3 >\approx 0,12. > $

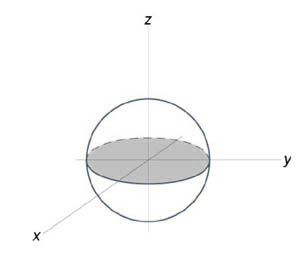
Вычислить объем единичного шара.

Решение:

Уравнение сферы радиусом (1) имеет вид ( < x^2 >+ < y^2 >+ < z^2 >= 1). В силу симметрии, ограничимся нахождением объема верхнего полушара и затем результат умножим на (2.) Уравнение верхней полусферы записывается как $z = \sqrt < 1 - \left( < < x^2 >+ < y^2 >>\right) > .$ Преобразуя это уравнение в полярные координаты, получаем $z\left( < r,\theta >\right) = \sqrt < 1 - < r^2 >> .$ В полярных координатах область интегрирования (R) описывается множеством (R = \left[< \left( < r,\theta >\right)|\;0 \le r \le 1,0 \le \theta \le 2\pi >\right].) Следовательно, объем верхнего полушара выражается формулой $ < < V_ < \large\frac < 1 > < 2 >\normalsize > > = \iint\limits_R < \sqrt < 1 - < r^2 >> rdrd\theta > > = < \int\limits_0^ < 2\pi > < d\theta >\int\limits_0^1 < \sqrt < 1 - < r^2 >> rdr > > = < 2\pi \int\limits_0^1 < \sqrt < 1 - < r^2 >> rdr > . > $ Сделаем замену переменной для оценки последнего интеграла. Пусть (1 — < r^2 >= t.) Тогда (-2rdr = dt) или (rdr = — \large\frac < < dt >> < 2 >\normalsize.) Уточним пределы интегрирования: (t = 1) при (r = 0) и, наоборот, (t = 0) при (r = 1.) Получаем $ < < V_ < \large\frac < 1 > < 2 >\normalsize > > = 2\pi \int\limits_0^1 < \sqrt < 1 - < r^2 >> rdr > > = < 2\pi \int\limits_1^0 < \sqrt t \left( < - \frac < < dt >> < 2 >>\right) > > = < - \pi \int\limits_1^0 < \sqrt t dt >> = < \pi \int\limits_0^1 < < t^ < \large\frac < 1 > < 2 >\normalsize > > dt > > = < \pi \left. < \left( < \frac < < < t^ < \large\frac < 3 > < 2 >\normalsize > > > > < < \frac < 3 > < 2 >> > >\right) >\right|_0^1 > = < \frac < < 2\pi >> < 3 >. > $ Таким образом, объем единичного шара равен $V = 2 < V_ < \large\frac < 1 > < 2 >\normalsize > > = \frac < < 4\pi >> < 3 >.$

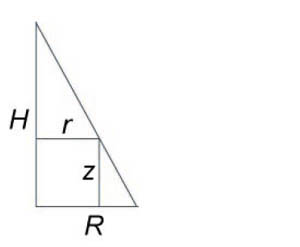
Используя полярные координаты, найти объем конуса высотой (H) и радиусом основания (R).

Решение:

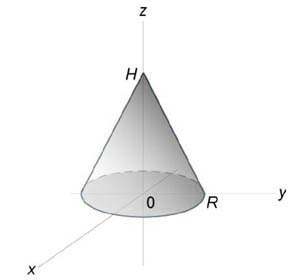
Далее:

Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности

Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных

Вычисление объёмов

Теорема об аналоге СДНФ в Pk

Свойства тройного интеграла

Равносильные формулы алгебры высказываний

Дифференциальные характеристики векторного поля

Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

Критерий полноты <формулировка>. Лемма о несамодвойственной функции

Лемма о построении множества $[F]_$

Булевы функции от $n$ переменных

Вычисление криволинейного интеграла второго рода в случае выполнения условия независимости от формы

Выражение площади плоской области через криволинейный интеграл

Определение двойного интеграла

Соленоидальное векторное поле

Огравление $\Rightarrow $