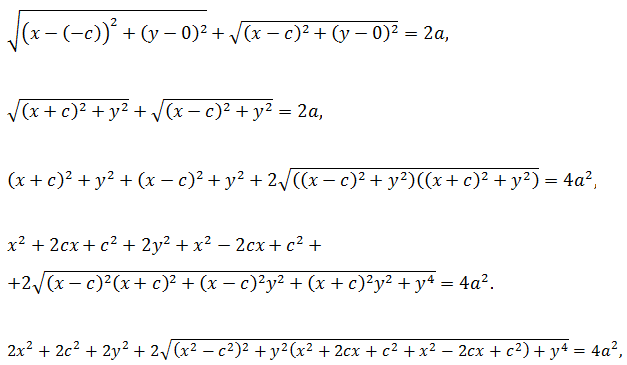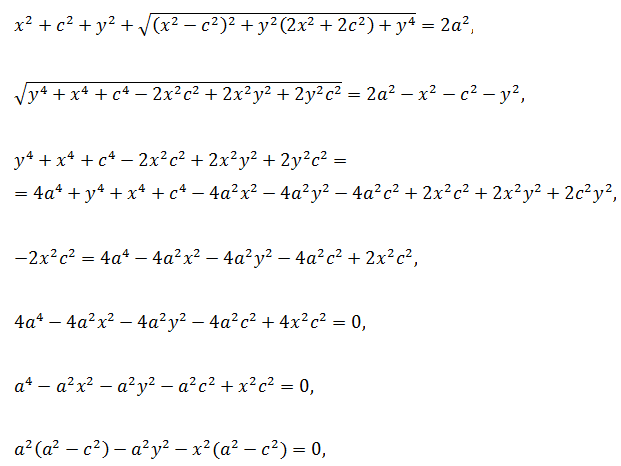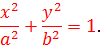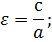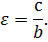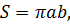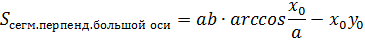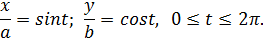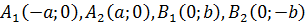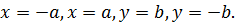Тема эллипс и его уравнение

Кривые второго порядка. Эллипс: формулы и задачи

Понятие о кривых второго порядка

Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.

Общий вид уравнения кривой второго порядка следующий:

,

где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.

При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.

Эллипс, заданный каноническим уравнением

Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.

Фокусы обозначены как и на рисунке ниже.

Каноническое уравнение эллипса имеет вид:

,

где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.

Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.

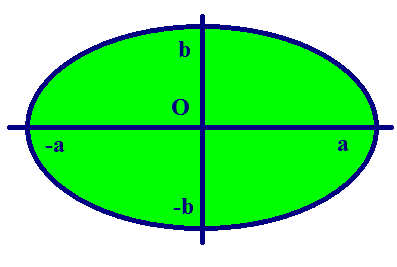
Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.

Если a = b , то уравнение эллипса принимает вид . Это уравнение окружности радиуса a , а окружность — частный случай эллипса. Эллипс можно получить из окружности радиуса a , если сжать её в a/b раз вдоль оси Oy .

Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.

Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:

Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.

Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.

Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5 , меньшая полуось — это b = 4 . Получаем каноническое уравнение эллипса:

.

Точки и , обозначенные зелёным на большей оси, где

,

называются фокусами.

называется эксцентриситетом эллипса.

Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.

Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.

Решение. Делаем несложные умозаключения:

— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,

— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.

Подставляем и вычисляем:

Результат — каноническое уравнение эллипса:

.

Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .

Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:

.

Вычисляем квадрат длины меньшей полуоси:

Составляем каноническое уравнение эллипса:

Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .

Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:

.

Получаем фокусы эллипса:

Решить задачи на эллипс самостоятельно, а затем посмотреть решение

Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:

1) расстояние между фокусами 30, а большая ось 34

2) малая ось 24, а один из фокусов находится в точке (-5; 0)

3) эксцентриситет , а один из фокусов находится в точке (6; 0)

Продолжаем решать задачи на эллипс вместе

Если — произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:

.

Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.

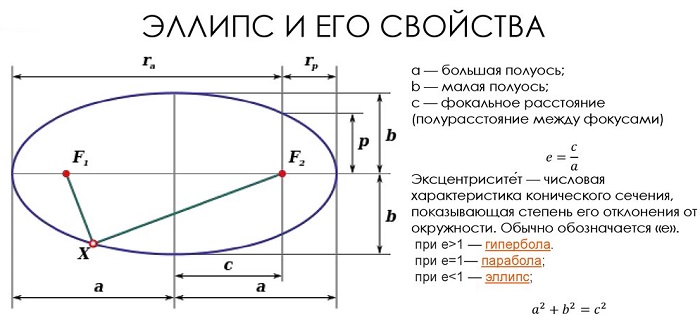
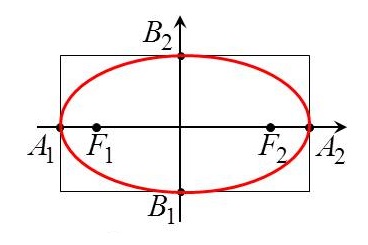
Прямые, определяемые уравнениями

,

называются директрисами эллипса (на чертеже — красные линии по краям).

Из двух вышеприведённых уравнений следует, что для любой точки эллипса

,

где и — расстояния этой точки до директрис и .

Пример 7. Дан эллипс . Составить уравнение его директрис.

Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:

.

Получаем уравнение директрис эллипса:

Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .

Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:

.

Теперь можем получить и квадрат длины меньшей полуоси:

Уравнение эллипса готово:

Пример 9. Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.

Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:

.

Получили единицу, следовательно, точка находится на эллипсе.

Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:

Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.

,

так как из исходного уравнения эллипса .

Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.

Урок по теме «Эллипс».

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

План-конспект урока по теме «Кривые второго порядка. Эллипс»

Русакова Елена Александровна

Тип урока: урок сообщения новых знаний, лекция с элементами беседы.

обеспечить понимание содержания учебного материала всеми учениками;

познакомить с понятием эллипса;

вывести каноническое уравнение эллипса;

изучить характеристики и исследовать свойства эллипса;

обеспечить применение знаний на практике;

сформировать умение составлять уравнения эллипса по различным исходным данным, изображать эллипс на координатной плоскости;

определять характеристики эллипса по каноническому и неканоническому уравнениям, по чертежу.

способствовать формированию положительного отношения к процессу учения;

способствовать формированию самостоятельности, аккуратности, внимательности, целеустремленности;

пробудить интерес к объектам и явлениям окружающего мира.

развивать коммуникативную культуру;

содействовать развитию способностей анализировать, формулировать, делать выводы;

развивать навыки осуществления само- и взаимоконтроля.

Средства обучения: учебник, компьютер, проектор, презентация, доска, магниты, шнур.

Форма организации урока: фронтальная, индивидуальная, парная.

Методы обучения: практический, наглядный, словесный, исследовательский.

Организационный момент ( 3 мин.)

Актуализация прежних знаний (12 мин.)

Изучение и первичное закрепление нового материала (55 мин.)

Домашняя работа (3 мин.)

Подведение итогов занятия. Рефлексия (7 мин.)

Организационный момент. Приветствие. Выявление отсутствующих.

Актуализация прежних знаний.

Записать уравнение окружности с центром в точке ( x ₀ ; y ₀ ) и радиусом r .

Записать уравнение окружности с центром в точке (5;-2) и радиусом 3.

Из уравнений x + y 2 =4; 6 x 2 +6 y 2 -12 x +36 y +59=0; x 2 +( y +4) 2 =3; xy =9; 5 x 2 +4 y 2 =6 выбрать те, которые задают окружность, указать ее центр и радиус.

Найти длину отрезка АВ, если А(7;3) и В(-1;5); А(-2;0), В(3;12).

Решить иррациональное уравнение (Ответ : x =5)

Учащиеся обмениваются тетрадями, проверяют правильность выполнения заданий, комментируют решение, дают определение окружности, вспоминают формулы сокращенного умножения, формулу расстояния между точками A ( x ₁ ; y ₁ ) и B ( x ₂ ; y ₂ ). На полях ставят «+» за каждое правильно решенное задание. В конце занятия по количеству «+» оценивается работа учащихся.

Изучение нового материала.

С помощью подручных средств (шнур, 2 магнита, доска) строим линию, обладающую следующим свойством: Сумма расстояний от любой точки данной линии до двух фиксированных точек (магнитов) есть величина постоянная, равная длине шнура. Построенная кривая называется эллипсом. Меняем длину шнура и расстояние между магнитами, получаем эллипсы разного размера и степени «сплющенности». Делаем вывод: для успешного построения длина шнура должна быть больше расстояния между магнитами.

Учащиеся записывают тему занятия, определения, выводы.

Определение . Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами , есть величина постоянная, большая, чем расстояние между фокусами.

Эллипсы вокруг нас.

Мозговой штурм. Где встречаются эллипсы в окружающем мире?

Первый закон Кеплера: Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.

Кратеры на Луне имеют форму эллипса.

Поверхность жидкости в наклоненном стакане.

Сечение конуса или цилиндра плоскостью.

Примеры эллипса в архитектуре (Колизей в Риме) и т.д.

Вывод уравнения эллипса.

Совместно с учащимися выбираем систему координат, записываем условие, которому удовлетворяет каждая точка эллипса, осуществляем преобразования).

Обозначим фокусы через F ₁ и F ₂ , расстояние между ними через 2 c , а сумму расстояний от произвольной точки эллипса до фокусов- через 2а. По определению 2 a >2 c , то есть a > c .

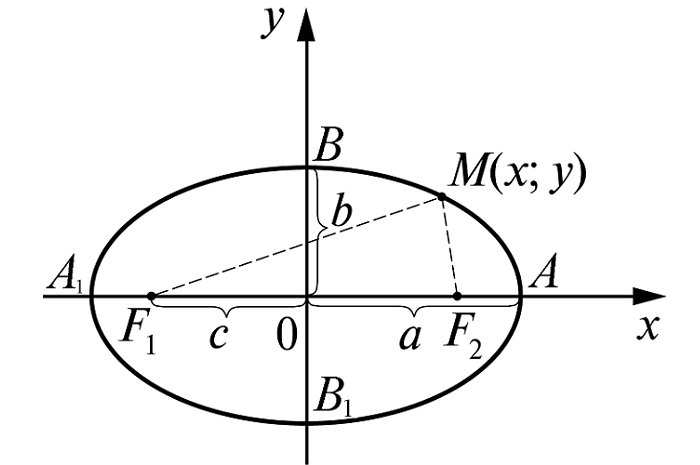
Для вывода уравнения эллипса выберем систему координат Oxy так, чтобы фокусы F ₁ и F ₂ лежали на оси Ox , а начало координат совпало с серединой отрезка F ₁ F ₂ . Тогда фокусы будут иметь следующие координаты: F ₁ (- c ;0) и F ₂ ( c ;0).

Пусть M ( x , y ) – произвольная точка эллипса. Тогда, согласно определению эллипса MF ₁ + MF ₂ =2 a , то есть

Это, по сути, и есть уравнение эллипса. Преобразуем его к более простому виду следующим образом:

Так как a > c , то a 2 — c 2 >0. Положим a 2 — c 2 = b 2 . Тогда последнее уравнение примет вид b 2 x 2 + a 2 y 2 = a 2 b 2 или (1)

Уравнение (1) называется каноническим уравнением эллипса. Эллипс-кривая второго порядка.

Исследование формы эллипса по его уравнению.

Учащиеся подставляют вместо x и y противоположные значения. Делают вывод.

(Если точка ( x ; y ) принадлежит эллипсу, то в силу четности степеней x и y ему также принадлежат точки ( x ,- y ), (- x , y ), (- x ,- y ). Вывод: эллипс симметричен относительно осей Ox и Oy , а также относительно точки O (0,0), которую называют центром эллипса.)

Как найти точки пересечения кривой с осями координат? (С осью Ох из условия y =0, с осью О y из условия x =0). Учащиеся находят точки пересечения эллипса с осями координат, решая соответствующие уравнения, делают вывод.

Вывод: Эллипс пересекает ось Ох в точках А ₁ ( a ;0) и А ₂ (-а;0), ось О y в точках B ₁ (0; b ) и B ₂ (0;- b ).

Определение. Точки А ₁ , А ₂ , В ₁ , В ₂ называются вершинами эллипса . Отрезки А ₁ А ₂ , В ₁ В ₂ , а также их длины 2 a и 2 b называются соответственно большой и малой осями эллипса. Числа a и b называют соответственно большой и малой полуосями эллипса.

Учащиеся сравнивают каждое слагаемое в левой части канонического уравнения с единицей, делают вывод.

(Вывод: Имеют место неравенства и , или — a ≤ x ≤ a , — b ≤ y ≤ b . Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми x =± a , y =± b .)

Учащиеся исследуют зависимость между x и y , делают вывод.

(Сумма неотрицательных слагаемых и равна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т.е. если | x | возрастает, то | y | уменьшается и наоборот.)

Вывод: Эллипс имеет форму, изображенную на рисунке:

Как изменится уравнение эллипса, если его фокусы расположим на оси ординат?

(Если фокусы эллипса лежат на оси Oy, то b>a, c 2 =b 2 – a 2 )

Как по каноническому уравнению эллипса определить его расположение?

(Решение комментируется учащимися по очереди, записывается в тетрадь)

№ 48. Составить уравнение эллипса, если две его вершины находятся в точках А ₁ (-6;0) и А ₂ (6;0), а фокусы- в точках F ₁ (-4;0) и F ₂ (4;0).

№ 49. Составить уравнение эллипса, если две его вершины находятся в точках B ₁ (-8;0) и B ₂ (8;0), а фокусы- в точках F ₁ (0;-6) и F ₂ (0;6).

№ 50. Составить уравнение эллипса, если расстояние между фокусами равно 6 (фокусы лежат на оси Ox ) и большая ось равна 10.

Дополнительные сведения об эллипсе

От чего зависит форма эллипса? От соотношения. Чаще в качестве характеристики формы эллипса используют отношение .

Определение. Отношение половины расстояния между фокусами к большой полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой ε: .

(Справка: эксцентриситет — от латинского ех — из, вне и centrum — центр.)

Оценить величину ε, сделать вывод.

(Так как 0 c a , то 0

Вывод: Чем меньше эксцентриситет эллипса, тем эллипс будет менее сплющенным. При ε=0 эллипс превращается в окружность.

(Решение комментируется учащимися, записывается в тетрадь)

№ 51. Вычислить эксцентриситет эллипса .

Решение: Из уравнения эллипса имеем a 2 =100, b 2 =51, по формуле a 2 — b 2 = c 2 найдем . Эксцентриситет находим по формуле ; ε=0,7.

№ 52. Составить уравнение эллипса, фокусы которого находятся в точках (-4;0) и (4;0), а эксцентриситет ε=0,8.

Решение: Из условия имеем c =4, . Находим a =5; b 2= 5 2 -4 2 =9. Следовательно, искомое уравнение имеет вид .

№ 53. Составить уравнение эллипса с фокусами на оси Ox , если его большая ось равна 14, а эксцентриситет.

Из условия имеем a =7, . Находим ; . Следовательно, искомое уравнение имеет вид или .

В течение 5 минут решить задачи № 60, №61самостоятельно, затем обменяться тетрадями, обсудить решение, сверить с ответами на доске, исправить в случае необходимости ошибки.

№ 60. Вычислить эксцентриситет эллипса а); б)

№ 61. Составить уравнение эллипса, фокусы которого находятся в точках и , а эксцентриситет . Ответ:

Определение. Пусть M ( x ; y ) – произвольная точка эллипса с фокусами F ₁ и F ₂ . Длины отрезков F ₁ M = r ₁ и F ₂ M = r ₂ называются фокальными радиусами точки M . Очевидно, r ₁ + r ₂ =2 a .

Имеют место формулы: r ₁ = a + x ; r ₂ = a — x

Определение. Прямые называются директрисами эллипса.

Справедлива теорема : Если r –расстояние от произвольной точки эллипса до какого-нибудь фокуса, d -расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение есть постоянная величина, равная эксцентриситету эллипса: .

(Если фокусы эллипса лежат на оси Oy, то b>a, c 2 =b 2 – a 2 , -эксцентриситет, — уравнения директрис.)

Для эллипса из №60(1) найти все известные элементы и характеристики, изобразить на координатной плоскости.

Уравнение эллипса с осями, параллельными координатным, имеет вид:

(2), где ( x ₀ ; y ₀ ) – координаты центра эллипса.

Как привести неканоническое уравнение эллипса к виду (2)?

Используем метод выделения полного квадрата.

Закрепление изученного: Найти координаты центра и оси эллипса, заданного уравнением 5 x 2 +9 y 2 -30 x +18 y +9=0.

y = b sin t, t ∈ [0; 2 π ]

являются параметрическими уравнениями эллипса (t — величина угла между осью Ox и прямой OM, соединяющей центр эллипса О с его точкой М).

Привести уравнение эллипса 4 x 2 +3 y 2 -8 x +12 y -32=0 к каноническому виду.

Построить эллипс с произвольными осями, задать его уравнением, найти все характеристики

Подведение итогов. Выставление отметок. Рефлексия.

Что такое эллипс?

Чем характеризуются точки эллипса?

Перечислить основные элементы и характеристики эллипса (фокусы, вершины, большая и малая оси, полуоси, центр, фокальные радиусы, директрисы).

Записать каноническое уравнение эллипса.

Как изменяется уравнение эллипса при параллельном переносе?

Как по уравнению определить расположение эллипса в системе координат?

Что на уроке показалось легким, что сложным?

Что вызвало наибольшие затруднения, над чем еще нужно поработать?

Богомолов Н.В., Практические занятия по математике, М., Юрайт, 2015.

Письменный Д.Т., Конспект лекций по высшей математике, М., Айрис пресс, 2014.

Кретов М.В., Виноградова Н.В., Сборник задач по высшей математике, издательство РГУ им.И.Канта, 2008.

Эллипс — свойства, уравнение и построение фигуры

Среди центральных кривых второго порядка особое место занимает эллипс, близкий к окружности, обладающий похожими свойствами, но всё же уникальный и неповторимый.

Определение и элементы эллипса

Множество точек координатной плоскости, для каждой из которых выполняется условие: сумма расстояний до двух заданных точек (фокусов) есть величина постоянная, называется эллипсом.

По форме график эллипса представляет замкнутую овальную кривую:

Наиболее простым случаем является расположение линии так, чтобы каждая точка имела симметричную пару относительно начала координат, а координатные оси являлись осями симметрии.

Отрезки осей симметрии, соединяющие две точки эллипса, называются осями. Различаются по размерам (большая и малая), а их половинки, соответственно, считаются полуосями.

Точки эллипса, являющиеся концами осей, называются вершинами.

Расстояния от точки на линии до фокусов получили название фокальных радиусов.

Расстояние между фокусами есть фокальное расстояние.

Отношение фокального расстояния к большей оси называется эксцентриситетом. Это особая характеристика, показывающая вытянутость или сплющенность фигуры.

Основные свойства эллипса

имеются две оси и один центр симметрии;

при равенстве полуосей линия превращается в окружность;

все точки фигуры лежат внутри прямоугольника со сторонами, равными большой и малой осям эллипса, проходящими через вершины параллельно осям.

Уравнение эллипса

Пусть линия расположена так, чтобы центр симметрии совпадал с началом координат, а оси – с осями координат.

Для составления уравнения достаточно воспользоваться определением, введя обозначение:

а – большая полуось (в наиболее простом виде её располагают вдоль оси Оx) (большая ось, соответственно, равна 2a);

c – половина фокального расстояния;

M(x;y) – произвольная точка линии.

В этом случае фокусы находятся в точках F₁(-c;0); F₂(c;0)

После ввода ещё одного обозначения

получается наиболее простой вид уравнения:

a 2 b 2 — a 2 y 2 — x 2 b 2 = 0,

a 2 b 2 = a 2 y 2 + x 2 b 2 ,

Параметр b численно равен полуоси, расположенной вдоль Oy (a > b).

В случае (b b) формула эксцентриситета (ε) принимает вид:

Чем меньше эксцентриситет, тем более сжатым будет эллипс.

Площадь эллипса

Площадь фигуры (овала), ограниченной эллипсом, можно вычислить по формуле:

a – большая полуось, b – малая.

Площадь сегмента эллипса

Часть эллипса, отсекаемая прямой, называется его сегментом.

Длина дуги эллипса

Длина дуги находится с помощью определённого интеграла по соответствующей формуле при введении параметра:

Радиус круга, вписанного в эллипс

В отличие от многоугольников, круг, вписанный в эллипс, касается его только в двух точках. Поэтому наименьшее расстояние между точками эллипса (содержащее центр) совпадает с диаметром круга:

Радиус круга, описанного вокруг эллипса

Окружность, описанная около эллипса, касается его также только в двух точках. Поэтому наибольшее расстояние между точками эллипса совпадает с диаметром круга:

Онлайн калькулятор позволяет по известным параметрам вычислить остальные, найти площадь эллипса или его части, длину дуги всей фигуры или заключённой между двумя заданными точками.

Как построить эллипс

Построение линии удобно выполнять в декартовых координатах в каноническом виде.

Строится прямоугольник. Для этого проводятся прямые:

Сглаживая углы, проводится линия по сторонам прямоугольника.

Полученная фигура есть эллипс. По координатам отмечается каждый фокус.

При вращении вокруг любой из осей координат образуется поверхность, которая называется эллипсоид.