Урок 6

уравнение Прямой с угловым коэффициентом.

уравнение Прямой, Проходящей через данную точку и имеющей данный угловой коэффициент.

уравнение Прямой, Проходящей через две данные точки.

Уравнение Прямой с угловым коэффициентом.

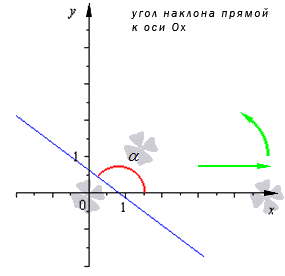
Пусть дана некоторая Прямая, не ПерПендикулярная оси ох. назовем углом наклона данной Прямой к оси ох угол а, на который нужно Повернуть ось ох, чтобы Положительное наПравление совПало с одним из наПравлений Прямой. угол а может Принимать различные значения, которые отличаются друг от друга на величину ± NП, где N — натуральное число. как Правило, в качестве угла наклона берут наименьшее неотрицательное значение угла а, на который нужно Повернуть (Против часовой стрелки) ось ох, чтобы ее Положительное наПравление совПало с одним из наПравлений Прямой. в этом случае 0

Тангенс угла наклона Прямой к оси ох называют угловым коэффициентом этой Прямой и обозначают буквой k: k= tgа (1) . из данного равенства следует, что если а=0, т.е. Прямая Параллельна оси ох, то k=0. если а=П/2, т.е. Прямая ПерПендикулярна к оси ох, то выражение k= tgа теряет смысл. в таком случае говорят, что угловой коэффициент «обращается в бесконечность».

Выведем уравнение данной Прямой, если известны ее угловой коэффициент k и величина b отрезка ов, который она отсекает на оси оу.

Пусть м — Произвольная точка Плоскости с координатами х и у. Проведем Прямые вN и Nм, Параллельные координатным осям, и Получим Прямоугольный треугольник вNм.

точка м лежит на Прямой тогда и только тогда, когда величины Nм и вN удовлетворяют условию: Nм / вN =tgа .

но Nм=см-сN=см-ов=у-b, вN=х. отсюда, учитывая формулу (1), Получаем, что точка м(х;у) лежит на данной Прямой тогда и только тогда, когда ее координаты удовлетворяют уравнению (у-b) / х=k, которое После Преобразований Примет вид у=kх+b (2) .

уравнение (2) называют уравнением Прямой с угловым коэффициентом . если k=0, то Прямая Параллельна оси ох и ее уравнение имеет вид у=b.

итак, уравнение любой Прямой, не ПерПендикулярной оси ох, имеет вид (2). очевидно, верно и обратное: любое уравнение вида (2) оПределяет Прямую, имеющую угловой коэффициент k и отсекающую на оси оу отрезок, величина которого b.

Пример 1 . составить уравнение Прямой, отсекающей на оси оу отрезок b=3 и образующий с осью ох угол а=п/4.

Решение. находим угловой коэффициент: k= tgа = tgа/ 4=1. Подставив k и b в равенство (2), Получим искомое уравнение Прямой: у=1х+3 или у-х-3=0.

Пример 2. Построить Прямую, заданную уравнением у=0,75х+2.

решение. отложим на оси оу отрезок ов, величина которого равна 2, Проведем через точку в Параллельно оси ох отрезок, величина которого вN=4, и через точку N Параллельно оси оу отрезок, величина которого Nм=3 (т.к. 0,75=3 / 4).

После этого Проводим Прямую вм, которая и является искомой. она имеет данный угловой коэффициент k=0,75=3 /4 и отсекает на оси оу отрезок величины b=2.

Уравнение Прямой, Проходящей через данную точку и имеющей данный угловой коэффициент.

в ряде случаев возникает необходимость составить уравнение Прямой, зная одну ее точку м 1 (х 1 ;у 1 ) и угловой коэффициент k . заПишем уравнение Прямой в виде (2), где b – Пока не известное число. так как Прямая Проходит через точку м 1 (х 1 ;у 1 ), то координаты этой точки удовлетворяют уравнению (2): у 1 = k х 1 + b . выразим из этого равенства b и Подставим его в уравнение (2), Получим искомое уравнение: у-у 1 = k (х – х 1 ) (3).

замечание. если Прямая Проходит ПерПендикулярно оси ох, т.е. ее угловой коэффициент обращается в бесконечность, то уравнение имеет вид х – х 1 =0. формально это уравнение можно Получить из уравнения (3), если разделить обе части уравнения (3) на k и затем устремить k к бесконечности.

Пример 3. составить уравнение Прямой, Проходящей через точку м(2;1) и образующий с осью ох угол а=45 0 .

решение. найдем угловой коэффициент: k = tgа = tg 45 0 =1. Подставим координаты точки м и значение углового коэффициента k в равенство (3), Получим уравнение Прямой: у-1=х-2 или у-х+1=0.

уравнение Прямой, Проходящей через две данные точки.

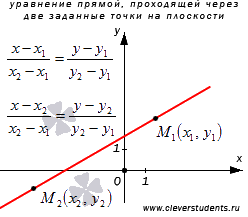
Пусть даны две точки м 1 (х 1 ;у 1 ) и м 2 (х 2 ;у 2 ). Приняв в уравнении (3) точку м(х;у) за м 2 (х 2 ;у 2 ), имеем у 2 – у 1 = k (х 2 – х 1 ). выразим из Последнего равенства k и Подставим его в уравнение (3), Получаем искомое уравнение:

это уравнение При условии, что у 1 не равен у 2 , можно заПисать так: (4)

если у 1 =у 2 , то уравнение искомой Прямой имеет вид у=у 1 . в этом случае Прямая Параллельна оси ох. если х 1 =х 2 , то Прямая Параллельна оси оу и ее уравнение имеет вид х=х 1 .

Пример 4. составить уравнение Прямой, Проходящей через точки а(3;1) и в(5;4).

решение. Подставив координаты точек а и в в равенство (4), Получаем искомое уравнение Прямой: = или 3х – 2у – 7 =0.

Автор: Вяликова Мария Владимировна — учитель математики и информатики высшей квалификационной категории МАОУ Пролетарская СОШ Новгородского района Новгородской области

Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач

Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.

Угол наклона прямой и угловой коэффициент прямой

Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.

Угол наклона прямой к оси О х , расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.

Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π ) .

Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.

Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.

Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.

Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.

Посчитать угловой коэффициент прямой при угле наклона равном 120 ° .

Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = — 3 .

Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k 0 , тогда угол тупой, что дает право определить его по формуле α = π — a r c t g k .

Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .

Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .

Ответ: α = a r c t g 3 .

Найти угол наклона прямой к оси О х , если угловой коэффициент = — 1 3 .

Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х . Отсюда k = — 1 3 0 , тогда необходимо применить формулу α = π — a r c t g k При подстановке получим выражение:

α = π — a r c t g — 1 3 = π — a r c t g 1 3 = π — π 6 = 5 π 6 .

Ответ: 5 π 6 .

Уравнение с угловым коэффициентом

Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси О у .

Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b . В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М , M 1 ( x 1 , y 1 ) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.

Задана прямая с угловым коэффициентом y = 1 3 x — 1 . Вычислить, принадлежат ли точки M 1 ( 3 , 0 ) и M 2 ( 2 , — 2 ) заданной прямой.

Необходимо подставить координаты точки M 1 ( 3 , 0 ) в заданное уравнение, тогда получим 0 = 1 3 · 3 — 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.

Если подставим координаты точки M 2 ( 2 , — 2 ) , тогда получим неверное равенство вида — 2 = 1 3 · 2 — 1 ⇔ — 2 = — 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.

Ответ: М 1 принадлежит прямой, а М 2 нет.

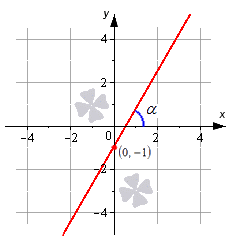
Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 ( 0 , b ) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b . Она образует угол α с положительным направлением оси О х , где k = t g α .

Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x — 1 . Получим, что прямая пройдет через точку с координатой 0 , — 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х . Отсюда видно, что коэффициент равен 3 .

Уравнение прямой с угловым коэффициентом, проходящей через заданную точку

Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 ( x 1 , y 1 ) .

Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 ( x 1 , y 1 ) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y — y 1 = k · ( x — x 1 ) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 ( x 1 , y 1 ) .

Составьте уравнение прямой, проходящей через точку М 1 с координатами ( 4 , — 1 ) , с угловым коэффициентом равным — 2 .

Решение

По условию имеем, что x 1 = 4 , y 1 = — 1 , k = — 2 . Отсюда уравнение прямой запишется таким образом y — y 1 = k · ( x — x 1 ) ⇔ y — ( — 1 ) = — 2 · ( x — 4 ) ⇔ y = — 2 x + 7 .

Ответ: y = — 2 x + 7 .

Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами ( 3 , 5 ) , параллельную прямой y = 2 x — 2 .

По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x — 2 , отсюда следует, что k = 2 . Составляем уравнение с угловым коэффициентом и получаем:

y — y 1 = k · ( x — x 1 ) ⇔ y — 5 = 2 · ( x — 3 ) ⇔ y = 2 x — 1

Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно

Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.

Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x — x 1 a x = y — y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y — b = k · x ⇔ k · x k = y — b k ⇔ x 1 = y — b k .

Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.

Привести уравнение прямой с угловым коэффициентом y = — 3 x + 12 к каноническому виду.

Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:

y = — 3 x + 12 ⇔ — 3 x = y — 12 ⇔ — 3 x — 3 = y — 12 — 3 ⇔ x 1 = y — 12 — 3

Ответ: x 1 = y — 12 — 3 .

Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x — y + b = 0 . Производится переход из общего уравнения прямой к уравнениям другого вида.

Дано уравнение прямой вида y = 1 7 x — 2 . Выяснить, является ли вектор с координатами a → = ( — 1 , 7 ) нормальным вектором прямой?

Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:

y = 1 7 x — 2 ⇔ 1 7 x — y — 2 = 0

Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , — 1 , отсюда 1 7 x — y — 2 = 0 . Понятно, что вектор a → = ( — 1 , 7 ) коллинеарен вектору n → = 1 7 , — 1 , так как имеем справедливое соотношение a → = — 7 · n → . Отсюда следует, что исходный вектор a → = — 1 , 7 — нормальный вектор прямой 1 7 x — y — 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x — 2 .

Решим задачу обратную данной.

Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим A x + B y + C = 0 ⇔ — A B · x — C B .

Результат и является уравннием с угловым коэффициентом, который равняется — A B .

Задано уравнение прямой вида 2 3 x — 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.

Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:

2 3 x — 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .

Ответ: y = 1 6 x + 1 4 .

Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x — x 1 a x = y — y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:

x a + y b = 1 ⇔ y b = 1 — x a ⇔ y = — b a · x + b .

Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:

x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ ⇔ a x · y = a y · x — a y · x 1 + a x · y 1 ⇔ y = a y a x · x — a y a x · x 1 + y 1

Имеется прямая, заданная уравнением x 2 + y — 3 = 1 . Привести к виду уравнения с угловым коэффициентом.

Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на — 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:

y — 3 = 1 — x 2 ⇔ — 3 · y — 3 = — 3 · 1 — x 2 ⇔ y = 3 2 x — 3 .

Ответ: y = 3 2 x — 3 .

Уравнение прямой вида x — 2 2 = y + 1 5 привести к виду с угловым коэффициентом.

Необходимо выражение x — 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · ( x — 2 ) = 2 · ( y + 1 ) . Теперь необходимо полностью его разрешить, для этого:

5 · ( x — 2 ) = 2 · ( y + 1 ) ⇔ 5 x — 10 = 2 y + 2 ⇔ 2 y = 5 x — 12 ⇔ y = 5 2 x

Ответ: y = 5 2 x — 6 .

Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.

Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = — 1 + 2 · λ .

Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:

x = λ y = — 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .

Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:

x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x — 1

Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .

Урок: Различные способы задания прямой в прямоугольной системе координат (уравнение прямой, заданной: двумя точками, точкой и угловым коэффициентом).

Актуализация знаний и умений

Задачи: психологическая подготовка ученика: сосредоточение внимания, осознание значимости предстоящей деятельности, возбуждение интереса к уроку; учащиеся воспроизводят известные им знания, осознают их, обобщают факты, связывают старые знания с новыми условиями, с новыми данными и т.д.

Актуализация знаний и умений.

1) Правила нахождения координат суммы двух векторов.

2) Правила нахождения координат разности двух векторов.

3) Правило нахождения произведения вектора на число.

4) Формула координат вектора через координаты его начала и конца.

5) Как найти координаты середины отрезка?

6) Как вычислить длину вектора по его координатам?

7) Как найти расстояние между двумя точками?

8) Уравнение прямой

9) Уравнение окружности

Давайте сформулируем тему урока

Просмотр содержимого документа
«Урок: Различные способы задания прямой в прямоугольной системе координат (уравнение прямой, заданной: двумя точками, точкой и угловым коэффициентом).»

Тема урока: Глава1. §7 Различные способы задания прямой в прямоугольной системе координат (уравнение прямой, заданной: двумя точками, точкой и угловым коэффициентом).

Оценка: на уроке оценивают результаты своей работы

Синтез: предлагают различные способы задания прямой в прямоугольной системе координат (уравнение прямой, заданной: двумя точками, точкой и угловым коэффициентом).

Анализ: изучают различные способы задания прямой в прямоугольной системе координат.

Применение: используют различные способы задания прямой в прямоугольной системе координат в решении задач, выполняют чертежи

Понимание: обсуждают различные способы задания прямой в прямоугольной системе координат

Знание: называют различные способы задания прямой в прямоугольной системе координат

познакомить учащихся с различными способами задания прямой в прямоугольной системе координат, обеспечить усвоение новых знаний по данной теме, научить работать с прямоугольной системой координат

развитие способности выражать мысли, познавательных способностей

развитие логического мышления

развитие умений вычленять главное в учебном материале

способствовать выявлению, раскрытию способностей учащихся, побуждать их к применению полученных знаний

побуждать учащихся к проявлению инициативы

побуждать к продуктивному мышлению

Учащиеся знают: различные способы задания прямой в прямоугольной системе координат

Учащиеся умеют:, решать задачи на применение уравнения прямой

Тип урока: сообщение новых знаний

Форма проведения урока: беседа

По источнику получения знаний: словесные, наглядные, практические.

По способу организации познавательной деятельности: объяснительно-иллюстративные, репродуктивные.

Методы воспитания: Организация деятельности, формирование мировоззрения, стимулирование деятельности, осуществление контроля, взаимоконтроля, самоконтроля.

Формы обучения: коллективные, индивидуальные, групповые

Основные понятия темы:

Задание на дом: № 201-202(неч), §7

Оборудование, ресурсы, наглядные пособия:

учебник, рабочая тетрадь, дидактический материал

Учитель: Шуринова Е.К.

Задачи: обеспечить нормальную внешнюю обстановку на уроке, психологически подготовить детей к общению

Проверка подготовленности к уроку

Организация внимания школьников

Ознакомление с планом проведения урока

Проверка домашнего задания.

Задачи: установить правильность, полноту и осознанность выполнения всеми учащимися домашнего задания, выявить пробелы в знаниях, устранить в ходе проверки обнаруженные пробелы

Выявление степени усвоения заданного учебного материала

Ликвидация обнаруженных недостатков.

Задачи: обеспечить включение школьников в совместную деятельность по определению целей учебного занятия.

Сообщение темы урока

Формулирование цели совместно с учениками

Показ значимости изучаемого материала

Актуализация знаний и умений

Задачи: психологическая подготовка ученика: сосредоточение внимания, осознание значимости предстоящей деятельности, возбуждение интереса к уроку; учащиеся воспроизводят известные им знания, осознают их, обобщают факты, связывают старые знания с новыми условиями, с новыми данными и т.д.

Актуализация знаний и умений.

1) Правила нахождения координат суммы двух векторов.

2) Правила нахождения координат разности двух векторов.

3) Правило нахождения произведения вектора на число.

4) Формула координат вектора через координаты его начала и конца.

5) Как найти координаты середины отрезка?

6) Как вычислить длину вектора по его координатам?

7) Как найти расстояние между двумя точками?

8) Уравнение прямой

9) Уравнение окружности

Давайте сформулируем тему урока

Изучение нового материала.

Задачи: обеспечить восприятие, осмысление и первичное запоминание изучаемого материала, осознание своих способов проработки учебной информации

Ознакомление с новым материалом.

уравнение прямой на плоскости в прямоугольной системе координат Oxy есть некоторое уравнение с

двумя переменными x и y, которое обращается в тождество при подстановке в него координат любой

точки этой прямой.

Всякое уравнение первой степени с двумя переменными x и y вида 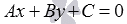, где

А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и всякая прямая на плоскости задается уравнением вида .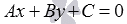

Уравнение прямой вида 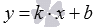, где x и y — переменные, а k и b – некоторые действительные числа, называется уравнением прямой с угловым коэффициентом (k – угловой коэффициент).

Закрепления новых знаний и умений.

Задачи: обеспечить повышение уровня осмысления учащимися изученного материала, глубины его усвоения

чтобы написать каноническое уравнение прямой a – координаты ее направляющего вектора и координаты лежащей на ней точки (и ). Оно имеет вид (или ).

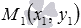
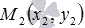
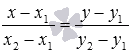
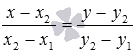
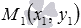
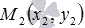
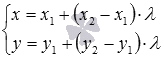
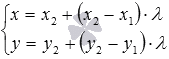
Также мы можем записать параметрические уравнения прямой на плоскости, проходящей через две точки и . Они имеют вид или .

Разберем решение примера.

Напишите уравнение прямой, которая проходит через две заданные точки .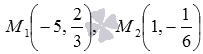

Мы выяснили, что каноническое уравнение прямой, проходящей через две точки с координатами 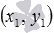и , имеет вид .

Из условия задачи имеем . Подставим эти данные в уравнение . Получаем .

.

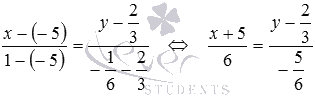
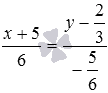
Если нам потребуется не каноническое уравнение прямой и не параметрические уравнения прямой, проходящей через две заданные точки, а уравнение прямой другого вида, то от канонического уравнения прямой всегда можно к нему прийти.

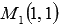
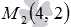
Составьте общее уравнение прямой, которая в прямоугольной системе координат Oxy на плоскости проходит через две точки и .

Сначала напишем каноническое уравнение прямой, проходящей через две заданные точки. Оно имеет вид . Теперь приведем полученное уравнение к требуемому виду: .

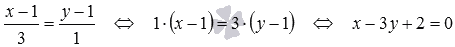
На этом можно и закончить с уравнением прямой, проходящей через две заданные точки в прямоугольной системе координат на плоскости. Но хочется напомнить, как мы решали такую задачу в средней школе на уроках алгебры.

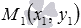
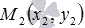
В школе нам было известно лишь уравнение прямой с угловым коэффициентом вида . Найдем значение углового коэффициента k и числа b, при которых уравнение определяет в прямоугольной системе координат Oxy на плоскости прямую линию, проходящую через точки и при . (Если же x₁=x₂, то угловой коэффициент прямой бесконечен, а прямую М₁М₂определяет общее неполное уравнение прямой вида x-x₁=0).

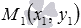
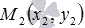
Так как точки М₁ и М₂ лежат на прямой, то координаты этих точек удовлетворяют уравнению прямой , то есть, справедливы равенства и . Решая систему уравнений вида относительно неизвестных переменных k и b, находим или . При этих значениях k и b уравнение прямой, проходящей через две точки и , принимает вид или .

Запоминать эти формулы не имеет смысла, при решении примеров проще повторять указанные действия.

Проверка новых знаний

Задачи: установить правильность и осознанность учащимися изученного материала, выявить пробелы первичного осмысления

Работа с учебником. Вопросы друг другу по данной теме

Задачи: скорректировать выявленные проблемы

Организация деятельности учащихся по коррекции выявленных недостатков

Повторное разъяснение учителя.

Подведение итогов. Рефлексия.

Задачи: инициировать рефлексию учащихся по поводу своего эмоционального состояния, дать оценку работе отдельных учащихся и всего класса