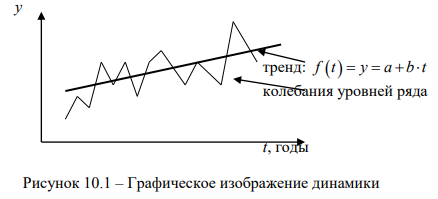
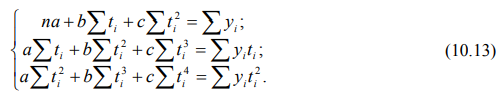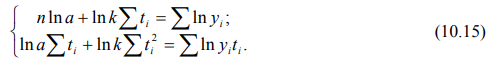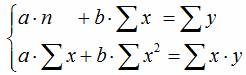Тенденции развития и колебания
Методические основы изучения основной тенденции развития
Уровни ряда динамики формируются под совокупным влиянием множества долговременных и краткосрочных факторов, и, в том числе, различного рода случайных обстоятельств. В связи с чем, при статистическом изучении динамики необходимо четко разделить ее на два основных элемента – тенденцию и колеблемость.
Тенденция развития динамического ряда к увеличению либо снижению его уровней – основная закономерность изменения уровней ряда. В отдельные же годы уровни испытывают колебания, отклоняясь от основной тенденции.
Тенденция динамики связана с действием долговременно существующих причин и условий развития. Однако после какого-то периода времени эти причины и условия тоже могут измениться и породить уже другую тенденцию развития изучаемого явления. Основная тенденция развития ряда динамики выражается в форме уравнения, называемого трендом.
Колебания, напротив, связаны с действием краткосрочных или циклических (конъюнктурных) факторов, влияющих на отдельные уровни динамического ряда, и отклоняющих уровни от тенденции то в одну, то в другую сторону. Например, положительная тенденция динамики урожайности связана с прогрессом агротехники, с укреплением экономического положения определенной совокупности хозяйств, совершенствованием организации производства. Колеблемость урожайности может быть вызвана, например, чередованием благоприятных по погоде и неблагоприятных лет, колебаниями в развитии вредных насекомых и болезней растений, и т.п.
Тенденцию и колебания наглядно показывает график (рис. 10.1). По оси абсцисс на графике всегда отражается время, по оси ординат – уровни ряда динамики. По обеим осям строго соблюдается масштаб, иначе характер динамики будет искажен.
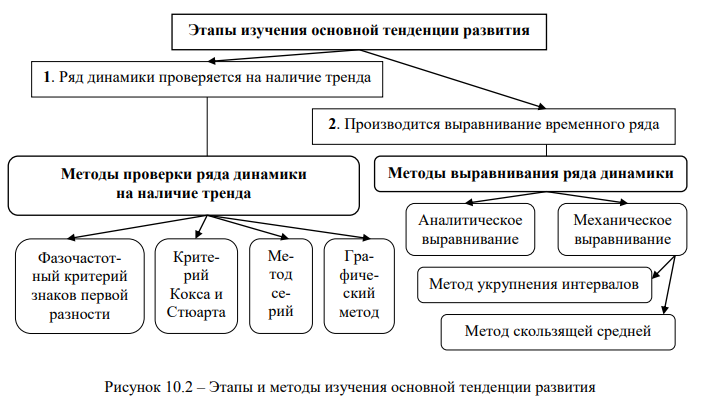
Изучение основной тенденции развития осуществляется в два этапа (рис. 10.2):
- на первом этапе ряд динамики проверяется на наличие тренда;
- на втором этапе проводится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов.
Проверка на наличие тренда в ряду динамики может быть осуществлена различными методами, в частности, приведенными на рис. 10.2.
Суть фазочастотного критерия знаков первой разности (Валлиса и Мура) заключается в том, что наличие тренда в динамическом ряду утверждается в том случае, если этот ряд не содержит или содержит в приемлемом количестве фазы – изменения знака разности первого порядка.
Суть критерия Кокса и Стюарта сводится к тому, что весь анализируемый ряд динамики разбивается на три равные по числу уровней группы и сравнивают между собой суммарные или средние уровни первой и последней групп. Существенное различие между ними позволяет сделать вывод о наличии тренда. Если количество уровней ряда динамики не делится на три, то недостающие уровни можно добавить, например, используя для этого условные уровни, повторив значения стоящие крайними в ряду, или фактические уровни смежных с крайними периодов.
В соответствии с методом серий каждый конкретный уровень временного ряда считается принадлежащим к одному из двух типов: например, если, уровень ряда меньше медианного значения, то считается, что он имеет тип А, в противном случае – тип В. После замены числовых значений уровней ряда буквами А и В последовательность уровней временного ряда выступает как последовательность типов. В образовавшейся последовательности типов определяется число серий (R). Серией называется любая последовательность элементов одинакового типа, граничащая с элементами другого типа. Если во временном ряду общая тенденция к росту или снижению отсутствует, то количество серий является случайной величиной (для n >10) и оказывается в доверительном интервале, характеризуемом неравенством:
где R – среднее число серий, определяемое по формуле:
n – число уровней ряда; t – нормированное отклонение – параметр, назначаемый в соответствии с принятым уровнем доверительной вероятности Р (вероятности, с которой число серий может оказаться в доверительном интервале). Значения t приводятся в таблицах нормального распределения вероятностей.
Наиболее часто используемые сочетания t и Р приведены в таблице 6.3; σR – среднее квадратическое отклонение числа серий, которое рассчитывается по формуле:
Полученные границы доверительного интервала округляют до целых чисел, уменьшая нижнюю границу и увеличивая верхнюю.
При графическом методе тип тренда устанавливают путем размещения на поле графика эмпирических уровней. Концентрированное вокруг определенной кривой или хаотическое размещение эмпирических уровней ряда позволяет сделать вывод о наличии или отсутствии основной тенденции развития.
Пример проверки ряда динамики на наличие тренда
По данным таблицы 10.1 необходимо определить наличие тренда в ряду динамики числа браков на 1000 человек населения Российской Федерации в 2005-2018 гг.
| Годы | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Браки | 7,4 | 7,8 | 8,8 | 8,3 | 8,4 | 8,5 | 9,2 | 8,5 | 8,5 | 8,4 | 7,9 | 6,7 | 7,1 | 6,1 |
Для применения фазочастотного критерия знаков первой разности необходимо определить наличие роста или уменьшение рассматриваемого показателя от года к году рассматриваемого периода, т.е. знак «+» или «-» цепного абсолютного прироста (формула 9.2, с. 154), для наглядности представив результаты в таблице 10.2.
| Годы | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Знак | … | + | + | — | + | + | + | — | 0 | — | — | — | + | — |
Количество «+» и « — « оказалось одинаковым, что, на первый взгляд, однозначно свидетельствует об отсутствии какой-либо закономерности динамики браков в России в рассматриваемом периоде.
Для применения критерия Кокса и Стюарта необходимо представленный ряд динамики разбить на три равные части, для чего к нему добавим имеющиеся на период исследования в официальной статистике данные о числе браков на 1000 человек населения в 2004 году – 6,8‰.
Первая треть добавленного ряда будет охватывать данные 2004-2008 гг., а последняя – 2014- 2018 гг., соответственно: (6,8+7,4+7,8+8,8+8,3=39,1) и (8,4+7,9+6,7+7,1+6,1=36,2). Средний уровень числа браков на 1000 человек населения страны в 2004-2008 гг. и 2014-2018 гг. составил, соответственно: 39,1:5=7,82‰ и 36,2:5=7,24‰.
Численные различия рассматриваемого показателя по выделенным периодам не велики, что также не позволяет утверждать наличие определенного тренда заключения браков в Российской Федерации.
Для применения метода серий рассчитаем медианное значение числа браков на 1000 человек населения страны в 2005-2018 гг.
Упорядоченная по возрастанию последовательность числа браков на 1000 человек населения в 2005-2018 гг. приведена в таблице 10.3.
| № п./п. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Браки | 6,1 | 6,7 | 7,1 | 7,4 | 7,8 | 7,9 | 8,3 | 8,4 | 8,4 | 8,5 | 8,5 | 8,5 | 8,8 | 9,2 |
Так как ряд имеет четырнадцать значений уровней, то медиана будет равна половине суммы значений уровней седьмого и восьмого элемента упорядоченного ряда: Ме = 8,35 ‰.
К типу А относятся значения уровней рассматриваемого ряда динамики которые меньше медианного значения, к типу В – больше и ряд типов выглядит как ААВАВВВВВВАААА, отсюда число серий R = 5.
С вероятностью 0,954 найдем доверительный интервал, в котором может оказаться R, если количество серий является случайной величиной. Для этого предварительно найдем следующие показатели:
– с вероятностью 0,954 нормированное отклонение: t = 2 (см. табл. 10.1);
– среднее число серий: 7,5 (формула 10.2);
– среднее квадратическое отклонение числа серий: 1,803 (формула 10.3).
С вероятностью 0,954 можно утверждать, что количество серий случайная величина, если оно попадает в доверительный интервал 3 Исходный и выровненные методом скользящей средней ряды динамики выпуска продукции в течение месяца
Результаты расчетов скользящих сумм и скользящих средних приведены в 3-6 колонках таблицы 10.4.
Данные колонок 5 и 6 таблицы 10.4 показывают устойчивую тенденцию роста ежедневного выпуска продукции в течение месяца.
Аналитическое выравнивание рядов динамики
Под аналитическим выравниванием понимают определение основной проявляющейся во времени тенденции развития изучаемого явления, выраженной соответствующим уравнением регрессии. При этом развитие предстает как бы в зависимости только от течения времени, т.е. одного фактора — времени. В итоге выравнивания временного ряда получают наиболее общий, суммарный, проявляющий во времени результат действия всех причинных факторов. Отклонение конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически.
На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t), а затем анализируют поведение отклонений от тенденции.
Функцию f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса. Чаще всего при выравнивании используются следующие зависимости:
– линейная, выраженная уравнением:
f(t) = y = a + b×t; (10.4)
– параболическая, выраженная уравнением:
f(t) = y = a + b×t + c×t 2 ; (10.5)
– экспоненциальная, выраженная уравнением:
f(t) = y = a×k t ; (10.4)
где y – уровни, освобожденные от колебаний;
а – начальный уровень тренда в момент или период, принятый за начало отсчета времени t (t = 0);
t – номер периода;
b – среднегодовой абсолютный прирост; константа линейного тренда (параметр, показывающий, на сколько изменится результат при изменении времени на единицу);
с – квадратический параметр, равный половине ускорения; константа параболического тренда. Ускорение (Δ’i) как разность между абсолютным приростом за данный период и абсолютным приростом за предыдущий период одинаковой длительности рассчитывается по формуле:
Δ’i = Δi — Δ’i-1. (10.7)
k – коэффициент роста; константа экспоненциального тренда.
Выравнивать динамические ряды по уравнению прямой линии целесообразно тогда, когда более или менее постоянны цепные абсолютные приросты, т.е. тогда, когда уровни ряда изменяются приблизительно в арифметической прогрессии.
Выравнивание динамических рядов по уравнению квадратической параболы необходимо применять в тех случаях, когда изменение уровней ряда происходит с приблизительно равномерным ускорением или замедлением цепных абсолютных приростов.
Выравнивание по экспоненциальной функции целесообразно использовать тогда, когда уровни ряда динамики выявляют тенденцию постоянства цепных темпов роста, т.е. в случае изменения уровней ряда динамики в геометрической прогрессии.
Кроме выше рассмотренных существуют логарифмическая, гиперболическая, логистическая и др. формы тренда.
Для расчета параметров уравнения тренда обычно используют метод наименьших квадратов.
Для каждого типа тренда МНК дает систему нормальных уравнений, решая которую вычисляют параметры тренда.
Для линейного тренда нормальные уравнения МНК имеют вид:
где yi – уровни исходного ряда динамики;
ti – номера периодов или моментов времени;
n – число уровней ряда.
Систему можно упростить, перенеся начало отсчета времени ti в середину ряда. Тогда Σti будет равна 0 и система приобретет вид:
Отметим, что значение Σt 2 при четном числе n можно определить по формуле:
Для того, чтобы выйти на значение Σt 2 , полученное по формуле, при четном числе n шаг между ti и ti-1 или ti+1 принимается равным 2 года.
Для тренда, выраженного квадратической параболой, нормальные уравнения МНК имеют вид:
После переноса начала отсчета ti в середину ряда получим:
Для экспоненциального тренда нормальные уравнения МНК имеют вид:
После переноса начала отсчета ti в середину ряда получим:
Построив уравнение регрессии, проводят оценку его надежности. Это делается посредством F-критерия Фишера, рассчитываемого по формуле 8.15. Если Fфакт > Fтеор, то уравнение регрессии значимо, т.е. построенная модель адекватна фактической временной тенденции.
Пример аналитического выравнивания ряда динамики
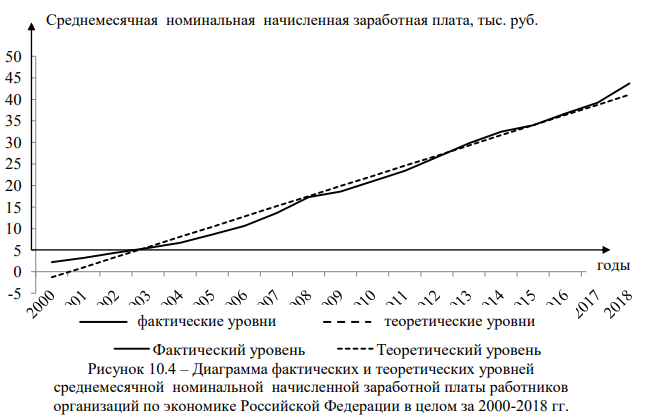
По данным таблицы 9.11 необходимо провести аналитическое выравнивание ряда динамики среднемесячной номинальной начисленной заработной платы работников организаций по экономике Российской Федерации в целом за 2000-2018 гг.
Проверку ряда динамики среднемесячной номинальной начисленной заработной платы работников организаций по экономике Российской Федерации за 2000-2018 гг. на наличие тренда проведем с помощью фазочастотного критерия знаков первой разности.
Данные таблицы 9.12 свидетельствуют о неуклонном росте среднемесячной заработной платы в стране и, соответственно, о положительных значениях знаков первой разности на протяжении всего исследованного периода.
Тенденция к росту уровней рассматриваемого ряда динамики очевидна.
Для определения тренда, наиболее точно отражающего закономерность изменения среднего уровня месячной заработной платы работников организаций по экономике Российской Федерации во времени, рассчитаем параметры уравнений линейной, параболической и экспоненциальной зависимостей, оценив их надежность с помощью F-критерия Фишера.
Результаты вспомогательных действий для расчета параметров уравнений регрессии приведены в таблице 10.5. Для упрощения расчетов начало отсчета времени ti перенесено в середину ряда.
| Годы | Среднемесячная зарплата, тыс. руб., уi, | Условное время, годы, ti | уiti | ti 2 | уiti 2 | ti 4 | Ln уiti | (Ln уiti)×ti | Уровни трендов | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| линейного | параболы II порядка | экспоненциального | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2000 | 2,2 | -9 | -19,8 | 81 | 178,2 | 6561 | 0,8 | -7,1 | -1,3 | -2,0 | 3,5 |
| 2001 | 3,2 | -8 | -25,6 | 64 | 204,8 | 4096 | 1,2 | -9,3 | 1,0 | 0,5 | 4,1 |
| 2002 | 4,4 | -7 | -30,8 | 49 | 215,6 | 2401 | 1,5 | -10,4 | 3,4 | 3,1 | 4,8 |
| 2003 | 5,5 | -6 | -33,0 | 36 | 198,0 | 1296 | 1,7 | -10,2 | 5,7 | 5,6 | 5,7 |
| 2004 | 6,7 | -5 | -33,5 | 25 | 167,5 | 625 | 1,9 | -9,5 | 8,1 | 8,2 | 6,6 |
| 2005 | 8,6 | -4 | -34,4 | 16 | 137,6 | 256 | 2,2 | -8,6 | 10,4 | 10,6 | 7,8 |
| 2006 | 10,6 | -3 | -31,8 | 9 | 95,4 | 81 | 2,4 | -7,1 | 12,8 | 13,1 | 9,1 |
| 2007 | 13,6 | -2 | -27,2 | 4 | 54,4 | 16 | 2,6 | -5,2 | 15,2 | 15,5 | 10,6 |
| 2008 | 17,3 | -1 | -17,3 | 1 | 17,3 | 1 | 2,9 | -2,9 | 17,5 | 17,9 | 12,4 |
| 2009 | 18,6 | 0 | 0 | 0 | 0 | 0 | 2,9 | 0,0 | 19,9 | 20,3 | 14,5 |
| 2010 | 21,0 | 1 | 21,0 | 1 | 21,0 | 1 | 3,0 | 3,0 | 22,2 | 22,6 | 17,0 |
| 2011 | 23,4 | 2 | 46,8 | 4 | 93,6 | 16 | 3,2 | 6,3 | 24,6 | 24,9 | 19,9 |
| 2012 | 26,6 | 3 | 79,8 | 9 | 239,4 | 81 | 3,3 | 9,8 | 26,9 | 27,2 | 23,3 |
| 2013 | 29,8 | 4 | 119,2 | 16 | 476,8 | 256 | 3,4 | 13,6 | 29,3 | 29,5 | 27,3 |
| 2014 | 32,5 | 5 | 162,5 | 25 | 812,5 | 625 | 3,5 | 17,4 | 31,7 | 31,7 | 31,9 |
| 2015 | 34,0 | 6 | 204,0 | 36 | 1224,0 | 1296 | 3,5 | 21,2 | 34,0 | 33,9 | 37,4 |
| 2016 | 36,7 | 7 | 256,9 | 49 | 1798,3 | 2401 | 3,6 | 25,2 | 36,4 | 36,1 | 43,7 |
| 2017 | 39,2 | 8 | 313,6 | 64 | 2508,8 | 4096 | 3,7 | 29,3 | 38,7 | 38,3 | 51,2 |
| 2018 | 43,7 | 9 | 393,3 | 81 | 3539,7 | 6561 | 3,8 | 34,0 | 41,1 | 40,4 | 59,9 |
| Всего | 377,6 | 0 | 1343,7 | 570 | 11982,9 | 30666 | 50,9 | 89,6 | 377,6 | 377,6 | 390,8 |
Рассчитаем параметры линейного тренда:
– начальный уровень тренда а в момент, принятый за начало отсчета времени (t = 0), по формуле 10.10 равен: 19,874 тыс. руб.;
– константа линейного тренда b по формуле 10.11 равна: 2,357 тыс. руб.
Уравнение линейного тренда имеет вид (формула 10.4): y = 19,874 + 2,357×t.
Параметры линейного уравнения означают, что среднемесячный уровень номинальной начисленной заработной платы работников организаций по экономике Российской Федерации в целом и его выровненный уровень, отнесенный к середине периода, т.е. к 2009 г., равняются 19,874 тыс. руб., а среднегодовой абсолютный прирост среднемесячной заработной платы за рассмотренный период составил 2,357 тыс. руб.
Рассчитаем параметры параболического тренда с помощью системы уравнений 10.14, установив начало отсчета времени (t = 0) в середине ряда, и осуществив соответствующую подстановку данных из столбцов 2-7 таблицы 10.5.
Полученная система имеет уравнений вид:
19a + 570c = 377,6;
570b = 1343,7;
570a + 30666c = 11982,9.
Решив эту систему уравнений имеем: a = 20,285, b = 2,357, c = -0,014.
Уравнение параболического тренда имеет вид (формула 10.5):
y = 20,285 + 2,357t + 0,014t 2 .
Значение параметра с (константы параболического тренда, равной половине ускорения изменения абсолютного цепного прироста) означает, что абсолютный прирост среднемесячной номинальной начисленной заработной работников организаций по экономике страны в рассматриваемом периоде замедлялся в среднем на 28 рубля (2×0,014×1000) в год. Сам же абсолютный прирост уже не является константой параболического тренда, а является средней величиной за период. В год, принятый за начало отсчета, т.е. 2009 г., тренд проходит через точку с ординатой 20,285 тыс. руб. Свободный член параболического тренда не является средним уровнем за период.
Рассчитаем параметры экспоненциального тренда, используя данные колонок 8 и 9 таблицы 10.5:
- по формуле 10.17 ln a = 2,679, отсюда, а = 14,543;
- по формуле 10.18 ln k = 0,157, отсюда k = 1,170.
Уравнение экспоненциального тренда имеет вид (формула 10.6): y = 14,543×1,17 t .
Значение параметра k (константы экспоненциального тренда) означает, что среднегодовой темп роста среднемесячной номинальной начисленной зарплаты работников организаций по экономике Российской Федерации в целом в 2000-2018 гг. составлял 117,0 %. В точке, принятой за начало отчета, тренд проходит точку с ординатой 14,543 тыс. руб.
Отметим, что суммы теоретических уровней линейного и параболического трендов (колонки 10 и 11 таблицы 10.5) совпадают с суммой фактических уровней среднемесячной заработной платы за 2000-2018 гг. (колонка 2 таблицы 10.5). Это свидетельствует не только о том, что параметры трендов рассчитаны правильно, но и позволяет предположить, что полученные уравнения регрессии адекватно характеризуют сложившуюся тенденцию.
Для составления прогнозов на будущее, рассмотренные тренды неравнозначны по степени адекватности отражения формы прогрессии уровней ряда динамики, поэтому проведем оценку надежности уравнений регрессии с помощью критерия Фишера при α = 0,05 (с вероятностью 0,95).
Рассчитаем теоретические и фактические значения F-критерия для линейного, параболического и экспоненциального трендов.
Для расчета общей и факторных дисперсий для всех видов трендов среднемесячной номинальной начисленной заработной платы работников организаций по экономике Российской Федерации в целом за 2000-2018 гг. построим вспомогательную таблицу 10.6.
| Годы | Среднемесячная зарплата, тыс. руб., уi, | уi 2 | Линейный тренд | Параболический тренд | Экспоненциальный тренд | |||
|---|---|---|---|---|---|---|---|---|
| y’i | (y’i— y ) 2 | y’i | (y’i— y ) 2 | y’i | (y’i— y ) 2 | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2000 | 2,2 | 4,84 | -1,3 | 450,13 | -2,0 | 480,29 | 3,5 | 267,04 |
| 2001 | 3,2 | 10,24 | 1,0 | 355,66 | 0,5 | 373,46 | 4,1 | 247,74 |
| 2002 | 4,4 | 19,36 | 3,4 | 272,30 | 3,1 | 280,97 | 4,8 | 226,08 |
| 2003 | 5,5 | 30,25 | 5,7 | 200,06 | 5,6 | 202,39 | 5,7 | 201,99 |
| 2004 | 6,7 | 44,89 | 8,1 | 138,93 | 8,2 | 137,32 | 6,6 | 175,51 |
| 2005 | 8,6 | 73,96 | 10,4 | 88,91 | 10,6 | 85,33 | 7,8 | 146,89 |
| 2006 | 10,6 | 112,36 | 12,8 | 50,01 | 13,1 | 46,03 | 9,1 | 116,63 |
| 2007 | 13,6 | 184,96 | 15,2 | 22,23 | 15,5 | 18,99 | 10,6 | 85,65 |
| 2008 | 17,3 | 299,29 | 17,5 | 5,56 | 17,9 | 3,84 | 12,4 | 55,45 |
| 2009 | 18,6 | 345,96 | 19,9 | 0,00 | 20,3 | 0,17 | 14,5 | 28,41 |
| 2010 | 21,0 | 441,00 | 22,2 | 5,56 | 22,6 | 7,59 | 17,0 | 8,14 |
| 2011 | 23,4 | 547,56 | 24,6 | 22,23 | 24,9 | 25,72 | 19,9 | 0,00 |
| 2012 | 26,6 | 707,56 | 26,9 | 50,01 | 27,2 | 54,17 | 23,3 | 11,81 |
| 2013 | 29,8 | 888,04 | 29,3 | 88,91 | 29,5 | 92,57 | 27,3 | 54,84 |
| 2014 | 32,5 | 1056,25 | 31,7 | 138,93 | 31,7 | 140,55 | 31,9 | 145,20 |
| 2015 | 34,0 | 1156,00 | 34,0 | 200,06 | 33,9 | 197,74 | 37,4 | 305,76 |
| 2016 | 36,7 | 1346,89 | 36,4 | 272,30 | 36,1 | 263,77 | 43,7 | 568,71 |
| 2017 | 39,2 | 1536,64 | 38,7 | 355,66 | 38,3 | 338,29 | 51,2 | 979,22 |
| 2018 | 43,7 | 1909,69 | 41,1 | 450,13 | 40,4 | 420,95 | 59,9 | 1600,40 |
| Всего | 377,6 | 10715,74 | 377,6 | 3167,60 | 377,6 | 3170,15 | 390,8 | 5225,47 |
Общую дисперсию рассчитываем по данным колонок 2 и 3 таблицы 10.6, используя способ разности (формула 5.12),
169,0. Факторную дисперсию по теоретическим значениям рассчитываем по формуле 8.9, а остаточную дисперсию – по формуле 8.11. Напомним, что у = 19,874 тыс. руб.
Для линейного тренда:
- факторная дисперсия по данным столбца 5 таблицы 10.6 равна: 166,7;
- остаточная дисперсия: = 169,0 – 166,7 = 2,3.
Для тренда, характеризуемого параболой второго порядка:
- факторная дисперсия по данным столбца 7 таблицы 10.6 равна: 166,9;
- остаточная дисперсия: = 169,0 – 166,9 = 2,1.
Для экспоненциального тренда:
- факторная дисперсия по данным столбца 9 таблицы 10.6 равна: 275,0;
- остаточная дисперсия: 169,0 – 275,0 = -106,0.
Фактическое значение критерия Фишера для каждого типа тренда определим по формуле 8.15, а значения степеней свободы k1 и k2 дисперсий – по формулам 8.16 и 8.17.
Итак, для линейного тренда при k1 = 2 – 1 = 1 и k2 = 19 – 2 = 17 фактическое значение критерия Фишера равно: 1232,1; теоретическое значение критерия Фишера по данным таблицы 7.10 равно: Fт ≈ 4,4. Так как Fф > Fт (1232,1 > 4,4), то с вероятностью 0,95 можно утверждать, что линейная регрессия адекватно отражает динамику среднемесячной номинальной начисленной заработной платы работников организаций по экономике Российской Федерации в целом в 2000-2018 гг.
Для тренда, характеризуемого параболой второго порядка, при k1 = 3 – 1 = 2 и k2 = 19 – 3 = 16 фактическое значение критерия Фишера равно: 635,8; теоретическое значение критерия Фишера по данным таблицы 7.10 равно: Fт = 3,6. Так как Fф > Fт (635,8 > 3,6), то с вероятностью 0,95 можно утверждать, что и параболическая регрессия адекватно отражает динамику номинальной среднемесячной заработной платы работников организаций России в 2000-2018 гг.
Для экспоненциального тренда фактическое значение критерия Фишера равно отрицательной величине, что не позволяет рассматривать данный тренд на предмет адекватности.
Наиболее адекватно сложившуюся в исследуемом ряду динамики тенденцию отражает линейный тренд (рис. 10.4).
Понятие о колеблемости
При изучении и измерении тенденции динамики колебания уровней играли лишь роль помех, «информационного шума», от которого следовало по возможности абстрагироваться. Однако факторы, обусловливающие колебания уровней временного ряда, как правило, объективны, что предопределяет самостоятельное исследование колеблемости.
Значение изучения колебаний уровней динамического ряда определяется, в первую очередь, тем, что регулирование рыночной экономики, как со стороны государства, так и производителей в значительной мере состоит в регулировании колебаний экономических процессов. Например, колебания урожайности, продуктивности скота, производства сельхозпродукции экономически нежелательны, так как потребность в продукции агрокомплекса постоянна. Эти колебания следует уменьшать, применяя прогрессивную технологию и другие меры. Напротив, сезонные колебания объемов производства зимней и летней одежды, обуви, мороженного, прохладительных напитков и т.п. – необходимы и закономерны, так как спрос на эти товары тоже колеблется по сезонам и равномерное производство требует лишних затрат на хранение запасов.
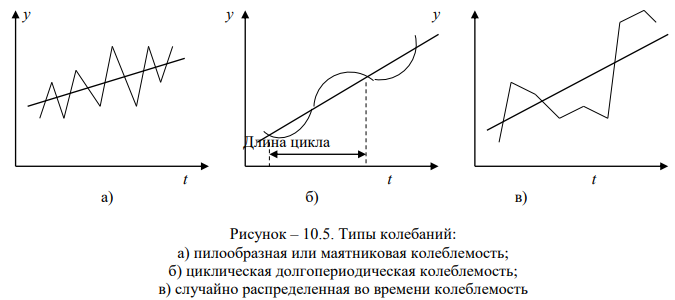
Типы колебаний статистических показателей весьма разнообразны. Три основных типа колебаний: пилообразная или маятниковая колеблемость, циклическая долгопериодическая колеблемость и случайно распределенная во времени колеблемость показаны на рис. 10.5, на котором хорошо видны их свойства и отличия друг от друга.
Пилообразная или маятниковая колеблемость состоит в попеременных отклонениях уровней ряда от тренда то в одну, то в другую сторону. Такие колебания можно наблюдать в динамике урожайности при невысоком уровне агротехники: высокий урожай при благоприятных условиях погоды выносит из почвы больше питательных веществ, чем их образуется естественным путем за год, следовательно, почва обедняется, что вызывает снижение следующего урожая ниже тренда, который выносит меньше питательных веществ, чем образуется за год и плодородие возрастает, и т.д.
Циклическая долгопериодическая колеблемость свойственна, например, солнечной активности (10-летние циклы), а, значит, и связанным с ней на Земле процессами – урожайности отдельных культур в ряде районов, некоторым заболеваниям людей, растений и т.п. Для этого типа колеблемости характерны редкая смена знаков отклонений от тренда и кумулятивный эффект отклонений одного знака, который может тяжело отражаться на экономике. Зато эти колебания хорошо прогнозируются.
Случайно распределенная во времени колеблемость – нерегулярная, хаотическая. Она может возникнуть при наложении множества колебаний с разными по длительности циклами. Но может возникать и в результате столь же хаотической колеблемости главной причины существования колебаний, например суммы осадков за летний период, температуры воздуха в среднем за месяц в разные годы.
На предположении, что параметры тренда и колебаний сохраняются до прогнозируемого периода, т.е. на экстраполяции, основана методика статистического прогноза по тренду и колеблемости. Экстраполяция справедлива, если система развивается эволюционно в достаточно стабильных условиях.
Сезонные колебания
Особого внимания при изучении колеблемости заслуживают сезонные колебания. Сезонные колебания строго цикличны – повторяются через каждый год.
Сезонными колебаниями называют периодические колебания уровней, возникающие под влиянием смены времени года.
Роль сезонных колебаний велика в агропромышленном комплексе, торговле многими товарами, заболеваемости, строительстве, деятельности рекреационных учреждений, на транспорте.
Сезонность наносит большой ущерб народному хозяйству, связанный с неравномерным использованием оборудования и рабочей силы, с неравномерной загрузкой транспорта и т.д.
Для изучения сезонных колебаний необходимо иметь уровни за каждый месяц (квартал) года, а, чтобы сгладить случайные колебания и точнее измерить сезонные, их изучают за несколько лет.
Уровень сезонности и форма «сезонной волны» изучаются с помощью индексов сезонности.
Способы определения индексов сезонности зависят от наличия или отсутствия основной тенденции.
Индивидуальные индексы сезонности показывают, во сколько раз фактический уровень ряда в момент (интервал) времени t больше или меньше среднего уровня, соответствующего данному моменту (интервалу) времени, либо уровня, вычисляемого по уравнению тенденции f(t).
Индекс сезонности (It,сез), если тренда нет или он незначителен, рассчитывают по формуле:
где y t – средний уровень показателя по одноименным месяцам (кварталам) за ряд лет;
t – номер месяца (квартала);
y o – общий средний уровень показателя за период исследования.
При наличии тренда индекс сезонности определяется на основе методов, исключающих влияние тенденции. Порядок расчета индекса сезонности при наличии тренда следующий:
1) для каждого уровня (yt,i) определяются выровненные значения по тренду f(t) = yt,i;
2) рассчитываются индивидуальные индексы уровней исследуемых показателей для каждого месяца (квартала) каждого года по формуле:

где n – число лет (i = 1, …, n).
Совокупность исчисленных для каждого месяца годового цикла индексов сезонности характеризует «сезонную волну» развития изучаемого явления во внутригодовой динамике.
Пример расчета индексов сезонности при условии отсутствия четко выраженной тенденции изменения уровней ряда динамики
По данным таблицы 10.7 необходимо проанализировать внутригодовую динамику потерь рабочего времени на предприятиях города N по причине неявок персонала на работу в 2016-2018 гг.
| Годы | Месяцы | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| январь | февраль | март | апрель | май | июнь | июль | август | сентябрь | октябрь | ноябрь | декабрь | |
| 2016 | 186 | 165 | 192 | 80 | 48 | 54 | 52 | 78 | 35 | 64 | 221 | 175 |
| 2017 | 174 | 180 | 204 | 123 | 50 | 46 | 68 | 84 | 43 | 58 | 179 | 198 |
| 2018 | 182 | 174 | 165 | 126 | 68 | 42 | 47 | 65 | 54 | 74 | 187 | 170 |
Проверим ряд динамики потерь рабочего времени на предприятиях города N в 2016-2018 гг. на наличие тренда. Для этого рассчитаем годовые потери рабочего времени, т.е. проведем укрупнение месячных уровней в годовые, и определим темпы роста. Расчет базисных темпов роста в данном примере соответствует методике проверки ряда динамики на наличие тренда с помощью критерия Кокса и Стюарта.
Просуммировав месячные уровни, получили потери рабочего времени в 2016 г. – 1350 чел.- дн.; в 2017 г. – 1407 чел.-дн.; в 2018 г. – 1354 чел.-дн.
Базисные темпы роста потерь рабочего времени на предприятиях города N в 2016-2018 гг., рассчитанные по формуле 9.5, составили 100,3 % (1354 : 1350 × 100); цепные темпы роста потерь рабочего времени внутри этого периода, рассчитанные по формуле 9.6, составили в 2017 г. по сравнению с 2016 г. 104,2 % (1407 : 1350 × 100), а в 2018 г. по сравнению с 2017 г. – 96,2 % (1354 : 1407 × 100).
Рассчитанные значения темпов роста годовых уровней ряда динамики потерь рабочего времени на предприятиях города N в 2016-2018 гг., позволяют сделать вывод, что изучаемое явление не имеет четко выраженной тенденции к росту, поэтому индексы сезонности рассчитываются по формуле 10.19.
Средние уровни потерь рабочего времени по одноименным месяцам за три года ( y t) и их общий среднемесячный уровень за период исследования ( y o) найдем по формуле 4.21.
Результаты расчетов соответствующих индексов сезонности представим в таблице 10.8.
| Годы | Месяцы | Всего, чел.-дн. | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | ||
| 2016 | 186 | 165 | 192 | 80 | 48 | 54 | 52 | 78 | 35 | 64 | 221 | 175 | 1350 |
| 2017 | 174 | 180 | 204 | 123 | 50 | 46 | 68 | 84 | 43 | 58 | 179 | 198 | 1407 |
| 2018 | 182 | 174 | 165 | 126 | 68 | 42 | 47 | 65 | 54 | 74 | 187 | 170 | 1354 |
| Итого, чел.-дн. | 542 | 519 | 561 | 329 | 166 | 142 | 167 | 227 | 132 | 196 | 587 | 543 | 4111 |
| y t, чел.-дн. | 180,7 | 173,0 | 187,0 | 109,7 | 55,3 | 47,3 | 55,7 | 75,7 | 44,0 | 65,3 | 195,3 | 181,0 | х |
| It,сез, % | 158,2 | 151,5 | 163,8 | 96,0 | 48,5 | 41,4 | 48,7 | 66,3 | 38,5 | 57,2 | 171,3 | 158,5 | х |
Расчеты y t проводились следующим образом: y I = 542 : 3 = 180,7 чел.-дн.; y II = 519 : 3 = 151,5 чел.-дн.; и т.д.; y o = 4111 : 36 = 114,2 чел.-дн.
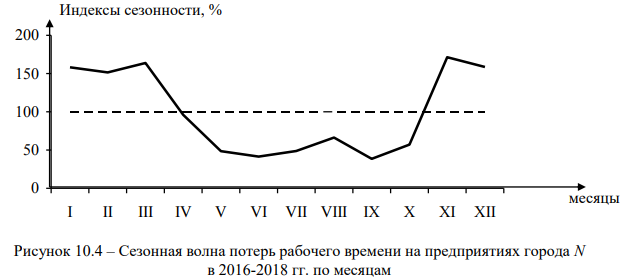
Наглядное представление о сезонной волне потерь рабочего времени на предприятиях города N дает график на рис. 10.4.
На рис. 10.4 четко видно, что наибольшие потери рабочего времени на предприятиях города N по причине неявок персонала на работу в 2016-2018 гг. приходились на март и ноябрь – пик сезонной заболеваемости острыми респираторными заболеваниями. Ярко выраженный спад потерь рабочего времени по причине неявок работников на предприятия города N приходился на период с мая по октябрь, что соответствует общей тенденции динамики потерь рабочего времени в экономике страны.
Пример расчета индексов сезонности при условии наличия тренда
По данным таблицы 10.9 необходимо проанализировать внутригодовую динамику потерь рабочего времени на предприятиях города К по причине неявок персонала на работу в 2016- 2018 гг.
Просуммировав внутригодовые уровни потерь рабочего времени на предприятиях города К по годам (2016 г. – 3010 чел.-дн.; 2017 г. – 2760 чел.-дн.; 2018 г. – 2510 чел.-дн.), видим наличие ярко выраженной тенденции их снижениях их уровня.
| Годы | Месяцы | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| январь | февраль | март | апрель | май | июнь | июль | август | сентябрь | октябрь | ноябрь | декабрь | |
| 2016 | 420 | 560 | 300 | 270 | 110 | 20 | 50 | 240 | 180 | 180 | 380 | 300 |
| 2017 | 340 | 480 | 250 | 260 | 180 | 70 | 40 | 170 | 130 | 220 | 370 | 250 |
| 2018 | 400 | 290 | 360 | 240 | 90 | 30 | 40 | 110 | 150 | 210 | 350 | 240 |
Для исключения влияния выявленной тенденции при анализе внутригодовой динамики потерь рабочего времени на предприятиях города К используем метод, основанный на аналитическом выравнивании уровней ряда.
Выравнивание уровней рассматриваемого ряда динамики по месяцам 2016-2018 гг. проведем, используя уравнение прямой (формула 10.4). Параметры линейного тренда рассчитаем по данным таблицы 10.10 упрощенным способом, выбрав начало отсчета t таким образом, чтобы было выполнено условие Σt = 0.
| Период | yt,i, чел.-дн. | t | yt,i×t | t 2 | y’t,i, чел.-дн. | it,i, % |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Январь 2016 г. | 420 | -35 | -14700 | … | 279 | 150,5 |
| Февраль 2016 г. | 560 | -33 | -18480 | … | 276 | 202,8 |
| Март 2016 г. | 300 | -31 | -9300 | … | 273 | 109,7 |
| Апрель 2016 г. | 270 | -29 | -7830 | … | 271 | 99,8 |
| Май 2016 г. | 110 | -27 | -2970 | … | 268 | 41,1 |
| Июнь 2016 г. | 20 | -25 | -500 | … | 265 | 7,5 |
| Июль 2016 г. | 50 | -23 | -1150 | … | 262 | 19,1 |
| Август 2016 г. | 240 | -21 | -5040 | … | 259 | 92,5 |
| Сентябрь 2016 г. | 180 | -19 | -3420 | … | 257 | 70,1 |
| Октябрь 2016 г. | 180 | -17 | -3060 | … | 254 | 70,9 |
| Ноябрь 2016 г. | 380 | -15 | -5700 | … | 251 | 151,4 |
| Декабрь 2016 г. | 300 | -13 | -3900 | … | 248 | 120,9 |
| Январь 2017 г. | 340 | -11 | -3740 | … | 245 | 138,5 |
| Февраль 2017 г. | 480 | -9 | -4320 | … | 243 | 197,9 |
| Март 2017 г. | 250 | -7 | -1750 | … | 240 | 104,3 |
| Апрель 2017 г. | 260 | -5 | -1300 | … | 237 | 109,7 |
| Май 2017 г. | 180 | -3 | -540 | … | 234 | 76,9 |
| Июнь 2017 г. | 70 | -1 | -70 | … | 231 | 30,3 |
| Июль 2017 г. | 40 | 1 | 40 | … | 229 | 17,5 |
| Август 2017 г. | 170 | 3 | 510 | … | 226 | 75,3 |
| Сентябрь 2017 г. | 130 | 5 | 650 | … | 223 | 58,3 |
| Октябрь 2017 г. | 220 | 7 | 1540 | … | 220 | 100,0 |
| Ноябрь 2017 г. | 370 | 9 | 3330 | … | 217 | 170,2 |
| Декабрь 2017 г. | 250 | 11 | 2750 | … | 215 | 116,5 |
| Январь 2018 г. | 400 | 13 | 5200 | … | 212 | 188,9 |
| Февраль 2018 г. | 290 | 15 | 4350 | … | 209 | 138,8 |
| Март 2018 г. | 360 | 17 | 6120 | … | 206 | 174,6 |
| Апрель 2018 г. | 240 | 19 | 4560 | … | 203 | 118,0 |
| Май 2018 г. | 90 | 21 | 1890 | … | 201 | 44,9 |
| Июнь 2018 г. | 30 | 23 | 690 | … | 198 | 15,2 |
| Июль 2018 г. | 40 | 25 | 1000 | … | 195 | 20,5 |
| Август 2018 г. | 110 | 27 | 2970 | … | 192 | 57,2 |
| Сентябрь 2018 г. | 150 | 29 | 4350 | … | 189 | 79,2 |
| Октябрь 2018 г. | 210 | 31 | 6510 | … | 187 | 112,5 |
| Ноябрь 2018 г. | 350 | 33 | 11550 | … | 184 | 190,4 |
| Декабрь 2018 г. | 240 | 35 | 8400 | … | 181 | 132,6 |
| Всего | 8280 | 0 | -21360 | 15540 | 8280 | х |
По формуле 10.10 и данным столбца 2 таблицы 10.10: а = 8280 : 36 = 230 чел.-дн.
По формуле 10.11 и данным столбцов 3 и 4 таблицы 10.10: b = -21360 : 15540 = -1,4 чел.-дн.
В соответствии с формулой 10.4 уравнение прямой выровненного ряда динамики потерь рабочего времени на предприятиях города К по причине неявок персонала на работу за 2016-2018 гг. имеет вид: y’t = 230 — 1,4×t.
На основании этого уравнения рассчитаем значения уровней выровненного ряда динамики y’t,i (см. столбец 6 табл. 10.10) и сопоставим с ними исходные уровни ряда yt,i, т. е. найдем индивидуальные индексы уровней исследуемых показателей для каждого квартала каждого года it,i, (см. столбец 7 табл. 10.10).
Индексы сезонности для каждого квартала определяем по формуле 10.21.
Так, для января индекс сезонности равен: 1,593 (159,3%); для февраля – 1,798 (179,8%); и т.д. Результаты расчетов индексов сезонности сведены в таблице 10.11.
| Месяцы | I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| It,сез, % | 159,3 | 179,8 | 129,5 | 109,2 | 54,3 | 17,7 | 19,0 | 75,0 | 69,2 | 94,5 | 170,7 | 123,3 |
Наглядное представление о внутригодовой динамике потерь рабочего времени на предприятиях города К по месяцам рассмотренного периода дает графическое изображение «сезонной волны» (рис. 10.4), отражающее наиболее высокие уровни потерь рабочего времени в феврале и ноябре.
Статистика: Учебник /Под ред. Елисеевой. — М., 2006. С.180-184
Оглавление
Средние показатели динамики – средний уровень ряда, средние абсолютные изменения и ускорения, средние темпы роста- используются при обобщении характеристик тенденции за длительный период, по различным периодам; при сравнении развития за неодинаковые по длительности отрезки времени и при выборе аналитического выражения тренда.
На практике для описания тенденции развития явления широко используются модели кривых роста.
Описание нескольких моделей кривых роста, форма которых соответствует характеру изменения динамического ряда, содержит следующий фрагмент учебника «Статистика»:
Типы уравнений тренда
«В настоящее время компьютерные программы анализа временных рядов предлагают достаточно широкий набор математических функций для построения уравнения тренда. Наиболее часто используются полиномы К-й степени, экспоненты, различного рода кривые с насыщением. В общем виде полином К-й степени представляет собой выражение:
При К=1 получаем линейный тренд:
По содержанию линейный тренд означает, что уровни динамического ряда изменяются с одинаковой скоростью.
Параметр а0 отражает начальный уровень ряда при t=0. Параметр a1 характеризует средний абсолютный прирост в единицу времени t.
Так, по уравнению тренда для индексов потребительских цен y = 99,9+1,9 t , где t = 1, 2…, 12 мес., видно, что ежемесячно цены возрастали в среднем на 1,9 процентных пункта. В линейном тренде уровни динамического ряда изменяются в арифметической прогрессии. Поэтому при прогнозировании по линейному тренду предполагаются падающие темпы роста уровня временного ряда.
При К=2 получаем параболу второй степени: 
Данная функция рекомендуется для прогнозирования, если ряд характеризуется стабильным абсолютным ускорением, т.е. постоянными являются вторые разности (приросты абсолютных приростов).
Параметр а0 – начальный уровень тренда при t = 0; а1– средний абсолютный прирост за рассматриваемый период времени, если t обозначено так, что 
Даже если тренд хорошо описывается параболой второй степени, то для долгосрочного прогноза в экономике он, как правило, затруднителен (особенно если а2
Рис. 9.7. График параболы третьей степени для уровней динамического ряда (а) и ее приростов (б)
В этом случае ряд характеризуется тремя этапами развития (рост, спад и опять рост), и при прогнозе на длительный период нет уверенности в правомерности и экстраполяции третьего периода. Кроме того, полиномы высоких степеней требуют достаточно длинных динамических рядов, чтобы параметры тренда были статистически надежными: на каждый параметр при t должно приходиться не менее 6-7 временных единиц. Следовательно, парабола третьей степени должна содержать ряд хотя бы в 20 лет, что предполагает достаточно стабильную экономику. Чаще отдают предпочтение функциям с меньшим числом параметров. Среди них широкое применение находит показательная кривая у=аb‘ или равносильная ей экспонента у=е a+bt . Эти функции рекомендуется использовать, если ряд динамики характеризуется стабильным темпом роста.
Следовательно, если за ряд лет динамика прибыли характеризуется уравнением вида: 
Если стабильными оказываются коэффициенты опережения темпов роста, то динамический ряд может быть описан логарифмической параболой:
Свое название данная функция получила потому, что, прологарифмировав ее, получим параболу второй степени: lgy = lga+tlgb+t 2 lgc.
Для этой функции темпы роста изменяются в одно и то же число раз.
Так, если дебиторская задолженность за ряд лет характеризуется уравнением: 
При подборе функций уравнений трендов можно использовать и другие их виды, параметры при которых не имеют экономической интерпретации. При этом применяются линеаризуемые функции, т.е. функции, приводимые к линейному виду. Так, при замедленном росте уровней динамического ряда может использоваться полулогарифмическая кривая: y=a+blnt. Она легко преобразовывается в линейную функцию, если заменить lnt на Т: y=a+bT. В 90-e годы по этой функции развивалось потребление в стране картофеля: y=93,1+11,81·lnt.
Среди функций, легко приводимых к линейному виду, можно назвать степенную: y=at b . Прологарифмировав ее, получим линейно-логарифмический тренд: lny=lna+blnt.
Заменив в нем lny на Y, lna на А, lnt на Т, придем к выражению линейного тренда: Y = A + bT
Степенная кривая предполагает разную меру пропорциональности изменений уровней динамического ряда во времени. При b>0 она характеризует непрерывный рост уровней, а при b b означает базисный коэффициент роста. Так, при t =1 y=a1 b =a; при t =2 y =а2 b ; при t = 3y =а3 b ; при t =4 у=а4 b и т.д.
Поэтому степенная функция практически сообщает о величине среднего темпа роста:
Например, обеспеченность городского населения Республики Коми жильем (кв. м общей площади на человека) за 1990-1999 гг. описывается уравнением тренда: lny=2,765+0,08lnt или при потенцировании: y=15,876t 0,08 . Из уравнения видно, что в 1990 г. теоретическое (расчетное) значение составляло 15,9 м 2 . Годы были обозначены как 1, 2. 10. Следовательно, за весь период обеспеченность населения жильем выросла в 1,202 раза (10 0,08 ), т.е. ежегодно она возрастала в среднем на 2,07%: (
В частном случае при b=- 1 уравнение степенного тренда превращается в гиперболу: y=a/t, асимптотами которой служат оси координат, а произведение у на t постоянно (у· t =а). Такого рода функцию можно видеть при изучении тенденций спроса на товары первой необходимости, если для них наблюдается рост цен за рассматриваемый период. В этом случае процент увеличения единицы времени t приводит к такому же уменьшению спроса.
Среди гипербол наибольшее распространение получили тренды следующего вида:
Гиперболические кривые характеризуются наличием асимптоты, выше или ниже которой признак не может принимать значения (верхняя или нижняя асимптоты).
При наличии понижающейся тенденции уровней ряда гипербола для прогноза предпочтительнее, чем, например, линейный тренд y=a-bt, ибо при увеличении значений t в уравнении линейного тренда возможно при прогнозе на дальнюю перспективу получить y 0, то значения уровней динамического ряда снижаются во времени и асимптотически приближаются к параметру a.
Например, отношение валютного курса рубля к паритету покупательной силы за период с мая 1995 г. по апрель 1996 г. характеризовалось уравнением тренда: y=1,396+0,707/t при r 2 =0,989. Оно демонстрирует понижающуюся тенденцию, при которой соотношение курса рубля и паритета покупательной силы не может быть меньше 1,396. Тенденция описывает 98,9% вариации уровней временного ряда, и лишь 1,1% дисперсии уровней ряда связано с действием случайных факторов.
Если b 0 уровни ряда имеют тенденцию к понижению и стремятся к 0 при неограниченном увеличении t, что в прогнозах практически не используется: в краткосрочных и среднесрочных прогнозах число прогнозных точек для t невелико. При b t и нижняя для функции y=c+ab t ).
Модифицированная экспонента применима, когда при прогнозе следует учитывать ограничение роста (или снижения) уровней динамического ряда. Так, при изучении тенденций роста уровня механизации труда в уравнение тренда может быть включена верхняя асимптота, равная 100%, – максимально возможный уровень, к которому стремится у. Если изучается динамика детской смертности, то речь может идти об установлении нижней асимптоты – значения у, ниже которого детская смертность не может быть исходя из достигнутых условий жизни.
Модифицированная экспонента служит базовой кривой для других кривых с насыщением, например, для логистической кривой. Тенденция развития явления при этом охватывает три этапа: вначале довольно медленный рост, который затем убыстряется и сменяется уменьшением роста и приближением уровня ряда к предельному значению, т. е. к уровню насыщения (см. график).
Рис. 9.8. Логистическая кривая
Логистическая кривая имеет следующий вид: 
Механизм развития производства новых товаров описывается иногда этой кривой. Г.Тинтнер применил данную функцию для описания тенденции роста численности шведского населения за 100 лет по 10-летним интервалам с 1850 по 1950 г.: 
Согласно этой кривой верхняя асимптота тенденции роста численности шведского населения составляла 10328806 человек (справка: в 1999 г. численность населения Швеции составляла 9,2 млн. человек).
Максимальное значение показателя с соответствует на графике отрезку кривой, параллельному оси абсцисс. Минимальное значение функции (y=0) будет при 
Метод аналитического выравнивания
Назначение сервиса . Сервис позволит прямо на сайте в онлайн-режиме провести аналитическое выравнивание ряда yt, проверить наличие гетероскедастичности и автокорреляции остатков тестом Дарбина-Уотсона (см. пример аналитического выравнивания по прямой).
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Чтобы привести нелинейные зависимости к линейной используют метод выравнивания (линеаризацию).
| y = f(x) | Преобразование | Метод линеаризации |
| y = b x a | Y = ln(y); X = ln(x) | Логарифмирование |
| y = b e ax | Y = ln(y); X = x | Комбинированный |
| y = 1/(ax+b) | Y = 1/y; X = x | Замена переменных |
| y = x/(ax+b) | Y = x/y; X = x | Замена переменных. Пример |
| y = aln(x)+b | Y = y; X = ln(x) | Комбинированный |
| y = a + bx + cx 2 | x1 = x; x2 = x 2 | Замена переменных |
| y = a + bx + cx 2 + dx 3 | x1 = x; x2 = x 2 ; x3 = x 3 | Замена переменных |
| y = a + b/x | x1 = 1/x | Замена переменных |
| y = a + sqrt(x)b | x1 = sqrt(x) | Замена переменных |
В общем случае при аналитическом выравнивании используется метод наименьших квадратов:
- Система нормальных уравнений для линейной зависимости:
- Система нормальных уравнений для полинома второй степени (параболы):
- Система нормальных уравнений для полинома третьей степени:
Типичное задание. Произведите аналитическое выравнивание и выразите общую тенденцию развития розничного товарооборота торгового дома соответствующим аналитическим уравнением. Вычислите аналитические (выровненные) уровни ряда динамики и нанесите их на график вместе с фактическими данными.
Пример . По УР имеются данные о вводе в действие жилых домов и общежитий, тыс. м 2 . Для анализа динамики показателя ввода в действие жилых домов и общежитий вычислите:
- абсолютные приросты, темпы роста и темпы прироста по годам и к 1998 г., абсолютное содержание одного процента прироста. Полученные показатели представьте в виде таблицы;
- среднегодовые показатели — величину уровня ряда; абсолютный прирост темп роста и прироста. Сделайте выводы.
Постройте график динамики уровня ряда за период 1998 -2006 гг., проведите аналитическое выравнивание ряда (постройте математическую модель и график), сделайте прогноз на 2007 год.
http://eos.ibi.spb.ru/umk/8_1/6/6_P4_R1_T7.html
http://math.semestr.ru/trend/analis.php