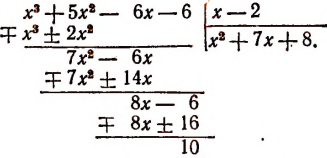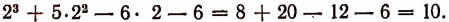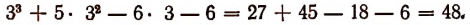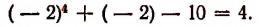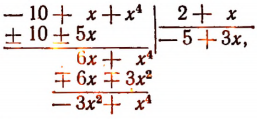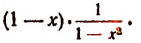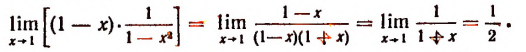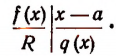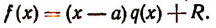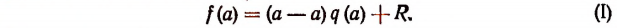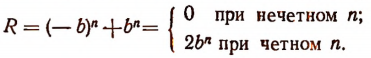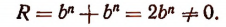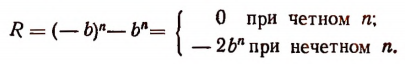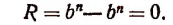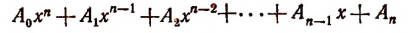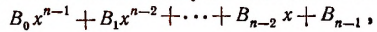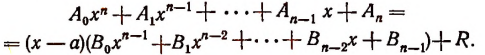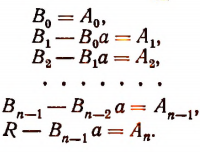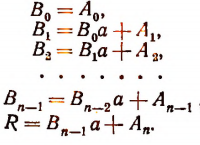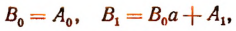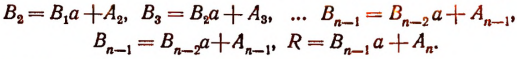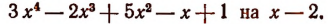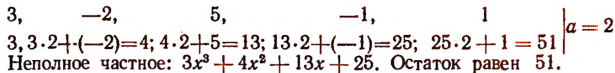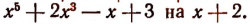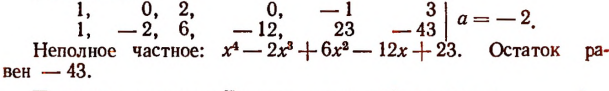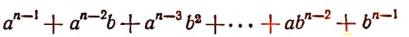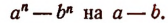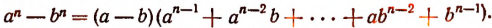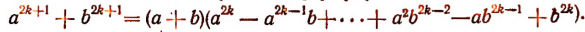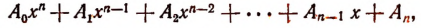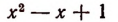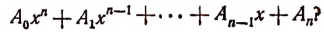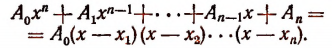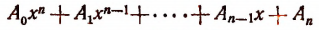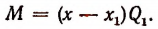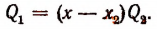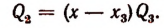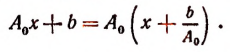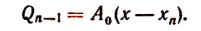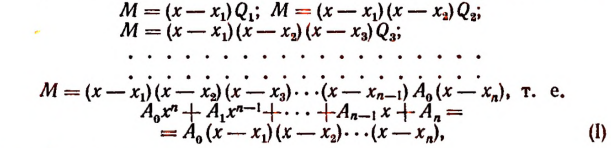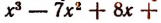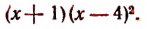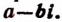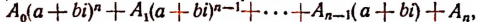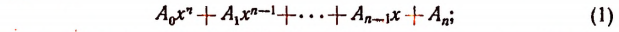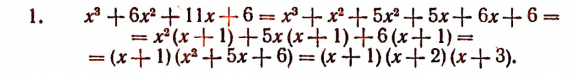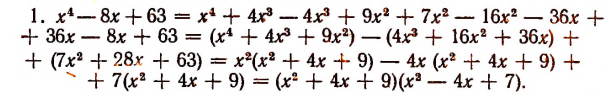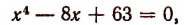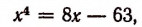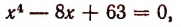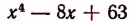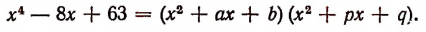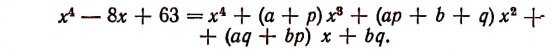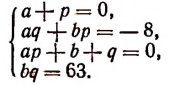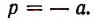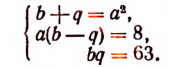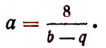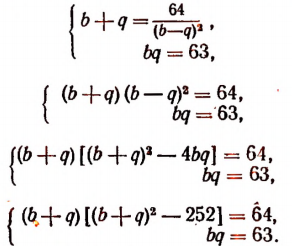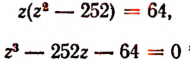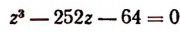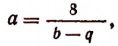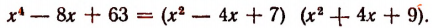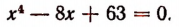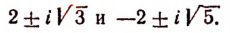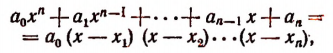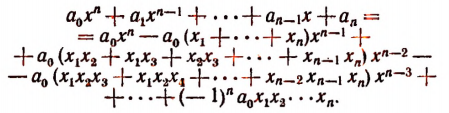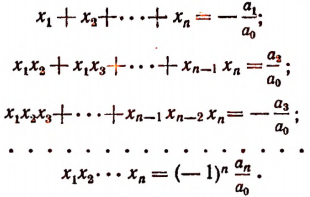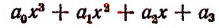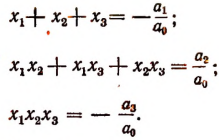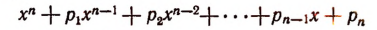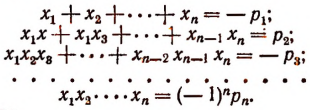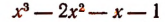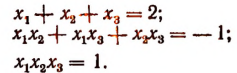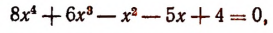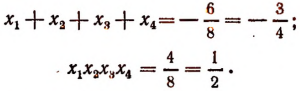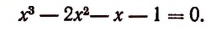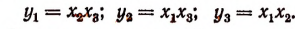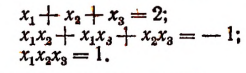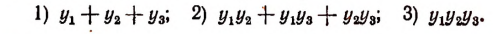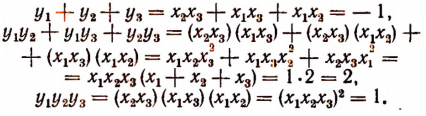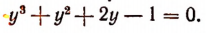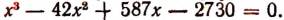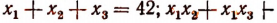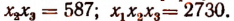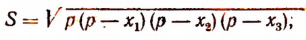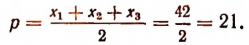Теорема Безу и ее применение в математике с примерами решения
Иллюстрация теоремы Безу на примерах:
Пусть требуется, например, разделить многочлен 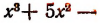
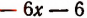
Можно предсказать, что остаток при этом делении будет равен 10. Проверим это:
Предсказание было сделано следующим образом.
Рассматривая делитель х—2, мы видим, что в нем из независимой переменной х вычитается число 2. Это число 2 мы подставили в делимое вместо переменного х и получили 10, т. е. как раз остаток.
Таким образом, оказалось, что остаток от деления многочлена на х—2 равен значению делимого при х = 2.
Это правило определения остатка, сформулированное в общем виде, и будет являться теоремой Безу.
При делении многочлена 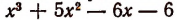
(Проверьте это непосредственным делением.)
При делении многочлена 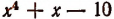
(Проверьте это непосредственным делением.)
При делении многочлена 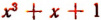
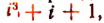
Приведенные примеры никак не могут рассматриваться как доказательства теоремы Безу: они даны лишь для того, чтобы облегчить понимание самой формулировки теоремы Безу.
Формулировка и доказательство теоремы Безу
При делении многочлена п-й степени относительно х, расположенного по убывающим степеням х, на двучлен (х — а остаток равен значению делимого при х = а
буква а может обозначать любое действительное или мнимое число, т. е. любое комплексное число).
Прежде чем доказывать теорему, сделаем несколько подготовительных пояснений.
1. В формулировке теоремы не случайно сказано: «расположенного по убывающим степеням х».
Если производить деление, расположив делимое и делитель по возрастающим степеням х, то тогда нельзя утверждать, что остаток всегда будет равен значению делимого при х = а.
Например, если многочлен 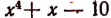
то мы никогда не получим остатка, равного числу 4, т. е. значению делимого при x = — 2.
2. Мы знаем, что существуют такие алгебраические выражения, которые теряют смысл при некоторых отдельных значениях входящих в него букв. Например, 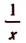
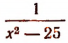
Заметим, что многочлен любой целой положительной степени никогда не теряет смысла. При всяком значении переменной он принимает определенное значение.
3. Произведение двух множителей, из которых один обращается в нуль, а другой принимает определенное значение, всегда равно нулю. Если же один множитель обращается в нуль, а другой теряет смысл, то о таком произведении нельзя говорить, что оно равно нулю. О таком произведении ничего определенного сказать нельзя. В каждом отдельном случае необходимо особое исследование.
Рассмотрим, например, произведение
При х = 1 первый множитель обращается в нуль, а второй теряет смысл. Нельзя утверждать, что это произведение при х = 1 равно нулю.
Итак, при х = 1 само произведение 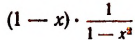
Доказательство теоремы Безу
Пусть f(x) обозначает собой произвольный многочлен n-й степени относительно переменной х, расположенный по убывающим степеням х, и пусть при делении на двучлен х — а получилось в частном q(x), а в остатке R (см. схему деления):
Очевидно, что q(х) будет некоторый многочлен (п — 1)-й степени относительно х, а остаток R будет величиной постоянной, т. е. не зависящей от х.
Если бы остаток R был многочленом хотя бы первой степени относительно х, то это означало бы, что процесс деления не доведен до конца. Итак, R от х не зависит
По свойству деления (делимое равно произведению делителя на частное плюс остаток) получим тождество
Это равенство справедливо прн всяком значении х, значит, оно будет справедливым и при х = а.
Подставляя в левую и правую части этого равенства вместо переменной х число а, получим:
Здесь символ f(a) обозначает собой уже не f(x) т.е. не многочлен относительно х, а значение этого многочлена при х = a.
q(а) обозначает значение q(x) при х = а.
Остаток R остался таким, каким он был раньше, так как R от х не зависит.
Произведение (а — a)q(a) равно нулю, так как множитель (а — а) равен нулю, а множитель q(a) есть определенное число. (Многочлен q(x) ни при каком определенном значении х не теряет смысла.)
Поэтому из равенства (I) получим:
что и требовалось доказать.
Пример:
При делении многочлена 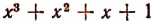
Следствия из теоремы Безу
Следствие 1. Если многочлен делится без остатка на х — а, то а необходимо будет корнем этого многочлена.
Следствие 2. Если а есть корень какого-либо многочлена, то это условие будет достаточным для делимости этого многочлена без остатка на х — а.
Эти два следствия можно объединить и выразить следующим образом:
Для делимости многочлена на x — а необходимо и достаточно, чтобы а было корнем этого многочлена.
Применения теоремы Безу
Поинтересуемся делимостью выражений вида 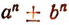
В выражении 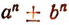
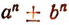
а) При делении 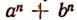
Значит, 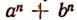
б) При делении 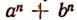
Значит, 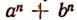
в) При делении 
Значит, 
г) При делении 
Значит, 
Другие важные применения теоремы Безу изложены в следующих главах.
Правило Горнера. Правило Горнера позволяет вычислять коэффициенты частного и остаток при делении многочлена, расположенного по убывающим степеням х, на двучлен х — а, не производя самого деления. При делении многочлена
на двучлен x — а в частном получим многочлен степени (п — 1):
а в остатке — некоторое число R.
По свойству деления
Раскрыв скобки в правой части этого равенства и объединив члены с одинаковыми степенями х, получим тот же многочлен, что и в левой части.
Приравнивая коэффициенты при одинаковых степенях х, найдем, что
Вычисления можно располагать так: коэффициенты делимого:
коэффициенты частного и остаток:
Примеры:
1. С помощью правила Горнера найти частное и остаток при делении многочлена
Решение:
2. Разделить
Решение:
Пользуясь правилом Горнера, легко найти частное
Отсюда вытекает формула
Аналогично можно получить и формулу
Теорема Гаусса
Если бы мы не знали никаких других чисел, кроме натуральных, то сказали бы, что уравнение 2х— 3 = 0 не имеет ни одного корня, так как нет ни одного натурального числа, которое удовлетворяло бы этому уравнению.
Уравнение 2х + 3 =0 не имеет ни одного корня в области положительных чисел.
Уравнение 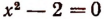
Уравнение 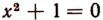
Выражение
в котором х есть независимая переменная, 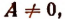
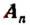
Корнем данной целой рациональной функции называется такое значение (действительное или мнимое) переменной х, при котором эта целая рациональная функция обращается в нуль.
В области действительных чисел не всякая целая рациональная функция имеет корень. Например, целая рациональная функция
не имеет ни одного действительного корня.
В связи с этим возникает следующий важный вопрос. Можно ли утверждать, что среди комплексных чисел найдется хоть одно число, являющееся корнем целой рациональной функции
Этот вопрос на протяжении длительного исторического периода оставался неразрешенным. В 1799 году Гаусс в возрасте 22 лет дал первое строгое доказательство теоремы о существовании корня целой рациональной функции.
Теорема Гаусса гласит: Всякая целая рациональная функция с любыми комплексными коэффициентами имеет по крайней мере один корень (действительный или мнимый).
В настоящее время существует несколько различных доказательств этой фундаментальной теоремы алгебры, но все они сложны и не входят в курс элементарной алгебры.
Теорема Гаусса еще раз свидетельствует нам ту общность в решении различных вопросов, которую придает им введение в науку комплексных чисел.
Свойства целой рациональной функции
Теорема Гаусса позволяет открыть и доказать другие важные свойства целой рациональной функции.
1. Всякую целую рациональную функцию п-й степени можно представить в виде произведения коэффициента высшего члена на п линейных множителей, т. е.
Эти линейные множители могут быть все действительными или все мнимыми и могут быть частью действительными и частью мнимыми.
Доказательство:
обозначим для краткости буквой М. По теореме Гаусса М имеет по крайней. мере один корень х, (действительный или мнимый). Тогда по следствию из теоремы Безу многочлен М должен делиться без остатка на 
Обозначив буквой 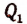
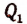
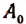
По теореме Гаусса функция 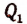
Обозначив этот корень буквой 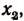
Число 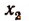
Применяя такие же рассуждения к функции 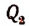
Степени функций 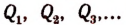
Продолжая этот процесс, мы придем к равенству
где 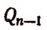
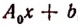
Обозначив корень функции 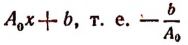

Пользуясь полученными равенствами, найдем последовательно:
что и требовалось доказать.
Из равенства (I) непосредственно видно, что числа 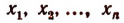
Правая часть равенства (I) не может обратиться в нуль ни при каком значении переменной х, отличном от значений
Следовательно, целая рациональная функция п-й степени не может иметь более п корней.
Если все числа 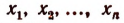
Если же среди чисел 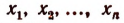
Пусть оказалось, что
а остальные корни отличны от 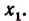
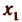
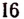
Значит, число — 1 есть простой ксрень, а число 4 есть корень кратности 2 или двукратный корень.
2. Если целая рациональная функция с действительными коэффициентами имеет комплексный корень 
в котором 
Заменив в последнем равенстве i числом —i, получим:
Теперь допустим, что 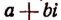
тогда окажется, что P + Qi = 0. Отсюда следует, что Р = 0 и Q = 0. Но в таком случае окажется равным нулю и выражение Р—Qi, т. е. окажется корнем целой рациональной функции (1) и число 
3. Всякая целая рациональная функция с действительными коэффициентами степени выше 2-й разложима либо на действительные линейные множители, либо на действительные множители 2-й степени, либо на действительные множители, среди которых имеются и линейные и второй степени. (Доказательство 3-го свойства опускается.)
Примеры разложения целой рациональной функции с действительными коэффициентами степени выше второй на действительные неприводимые множители
Получилось разложение на действительные линейные множители.
Получилось разложение на действительные множители 2-й степени.
Получился один множитель линейный, а другой 2-й степени.
Получился один множитель линейный, а другой 2-й степени.
Теоретически доказано (как уже отмечалось), что всякая целая рациональная функция с действительными коэффициентами степени выше 2-й разложима на действительные множители 1-й и 2-й степени.
Однако осуществление этого разложения не всегда достигается легко. Например, попробуем разложить на множители
Решим эту задачу двумя способами.
(Полученные многочлены 2-й степени имеют мнимые корни, а потому неразложимы на действительные линейные множители.)
Изложенный способ носит слишком искусственный характер. Его трудно придумать.
Второй способ, изложенный ниже, будет менее искусственным.
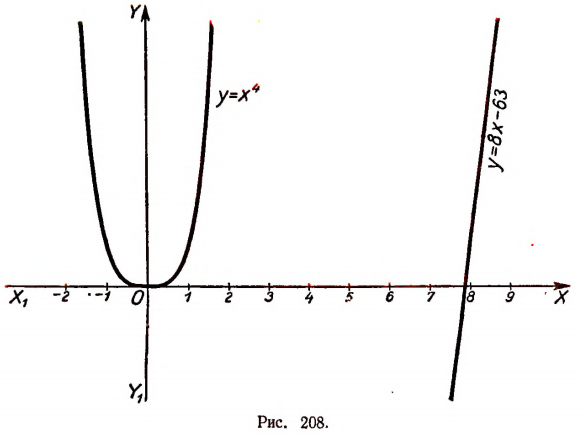
2. Прежде всего исследуем характер корней многочлена 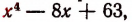
Переписав это уравнение в виде
построим графики функций 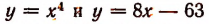
а значит, и многочлена
будут все мнимыми. Поэтому среди действительных множителей, на которые разлагается этот многочлен, не может быть ни одного линейного.
Итак, выяснено, что действительными множителями разложения многочлена 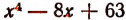
Таким образом, будем иметь, что
Остается определить а, b, р и q.
Перемножив многочлены, стоящие в правой части последнего равенства, получим:
Но поскольку нам необходимо, чтобы правая часть этого равенства превратилась в такой же многочлен, который стоит в левой части, потребуем выполнения следующих условий:
Получилась система четырех уравнений с четырьмя неизвестными a, b, р, q.
Из первого уравнения
Подставив во второе и третье уравнение — а вместо р, получим систему:
Из второго уравнения этой системы
Подставив это в первое уравнение, получим систему:
Обозначим b + q буквой z. Тогда первое уравнение последней системы примет вид:
Делителями числа 64 являются: ± 1; ± 2; ± 4; ± 8; ± 16; ± 32; ± 64.
Испытывая эти делители, обнаружим, что число 16 является корнем уравнения
Значит, мы можем взять b + q = 16. Кроме того, bq = 63. Отсюда примем b = 7 и q = 9. Пользуясь равенством
получим, что а = —4. Наконец, из равенства р = —а найдем, что р = — 4.
Теперь задача решена полностью. Мы получили:
Имея это разложение, мы легко обнаруживаем все корни многочлена 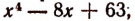
Этими корнями будут комплексные числа
Формулы Виета
Было доказано, что целая рациональная функция разлагается иа множители по формуле:
где 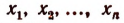
Сравнивая коэффициенты при одинаковых степенях буквы х в левой и правой частях последнего равенства, получим формулы:
Эти формулы носят название формул Виета, по имени открывшего их замечательного французского математика Франсуа Виета. Оии связывают корни и коэффициенты целой рациональной функции. Например, для
Для приведенной функции
формулы Виета принимают вид:
Примеры:
1. Не решая уравнения
найти сумму и произведение его корней.
Решение:
2. Пусть 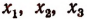
Составить новое уравнение, корнями которого были бы числа:
Решение:
Согласно формулам Виета
Теперь найдем значения трех выражений:
Легко видеть, что
Искомым уравнением будет
3. Сторонами треугольника являются корни уравнения
Не решая этого уравнения, найти площадь треугольника.
Решение:
Обозначим корни данного уравнения через 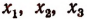
По формуле Герона
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Теорема Безу — формула, алгоритмы и примеры решения уравнений
Для облегчения процесса и используется теорема Безу, следствия из которой позволяют легко определять рациональные корни уравнений любой сложности. Но тут существует оговорка, что правило применимо лишь в том случае, если в задании стоят рациональные коэффициенты.
Основные понятия
Пожалуй, вместе со схемой Горнера, теорема Безу является лучшим способом решения уравнений высших степеней. Этьен Безу родился во Франции в 1730 году и в 28 лет стал членом Парижской академии наук. Именно он вместе с Крамером является родоначальником теории возникновения определителей. Математик, занимаясь алгеброй, смог найти алгоритм, позволяющий исключать неизвестные из уравнений высших порядков. При этом он смог доказать, что две кривые энного и эмного порядка могут пересекаться только в m — n точках.
С закономерностью Безу знакомят на уроках алгебры в седьмом классе средней школы. Согласно ей, при делении многочлена на двучлен остаток всегда будет равняться значению этого выражения в точке пересечения.
То есть, если имеется многочлен вида P (x), то при его делении на двучлен (x — a) получившийся остаток s будет численно равный значению делимого в точке a. В математической форме ответ можно записать как s = P (a).
Для понимания сути теоремы следует вспомнить деление двух многочленов методом «уголок». В этом случае происходит понижение степени с каждым действием. В итоге определяется частное и остаток. Так, согласно теореме, число a будет являться решением для многочлена. Иными словами, для выражения P (x), P (a) равняется нулю только тогда, когда значение a и есть корень уравнения. Например, для многочлена x 2 — 1, корнями будут числа минус один и единица, в то же время выражение x 3019 / 3 решения не имеет, так как равенство x 3019 / 3 = 0 невозможно.
К теореме существует два замечания:
- Под многочленом понимается приведённое выражение, когда коэффициент при старшей степени равняется единице. Например, x 2 + 3 x, x 5 — 2.
- При делении все коэффициенты многочлена частного должны оказаться целыми.
На этом и основана теорема Безу. Поэтому большее значение в математике имеет не сама теорема, а её следствие. Согласно ему, когда число a является решением, то остаток от выполнения операции деления на двучлен будет равняться нулю.
Другими словами, многочлен должен делиться на двучлен без остатка.
Суть открытия
Пусть имеется уравнение высшей степени вида P (x) = 0, где P (x) есть многочлен, состоящий из a0x n + a1x n-1 + … + an-1x + an. При этом на практике будет оказываться, что все коэффициенты являются целыми числами. Рассмотрим два многочлена: P (x) = x 3 + 3 x 2 -2 x +2 и Q (x) = x -1. Нужно найти остаток от деления P (x) на Q (x). Этим остатком должно быть число, так как его степень будет меньше чем та, на что происходит деление.
Для решения примера нужно использовать деление в столбик. Первым действием необходимо подобрать выражение таким образом, чтобы при умножении его на x-1 получилась кубическая степень. Этим выражением будет икс в квадрате. После выполнения действия получится одночлен: x 3 — x 2 . Подставив его под первый многочлен, можно получить меньшее на единицу порядка выражение: 4x 2 — 2x.
Чтобы получить это уравнение x-1 необходимо умножить на 4x. Отсюда получается снова выражение с меньшей степенью: 4x 2 — 4x. После вычитания образуется двучлен: 2 x +2. Для того чтобы от него избавиться x-1 следует умножить на двойку. В результате после вычитания получится остаток равный четырём.
Этот ответ на самом деле можно найти более простым способом используя определение Безу. Для рассматриваемого примера свободные коэффициенты в сумме будут давать: 1 + 3 — 2 + 2 = 4. Это число и является найденным остатком, получившимся после деления.
С помощью этой формулировки нахождение действительных корней любого уравнения выполнять совершенно несложно. Пусть эн будет корнем уравнения P (х) = 0. Тогда при подстановке его значения получится тождество — ноль равняется нулю. Это означает, что P (n) = 0, а вместе с функцией равный нулю и остаток при делении.
Таким образом, если удалось подобрать корень уравнения, то в соответствии с формулировкой Безу многочлен P (x) будет делиться на P (n) нацело. В этом и состоит главное применение теоремы Безу — решения примеров, состоящих из уравнений имеющие степени высокого порядка.
Фактически задача нахождения ответа в уравнениях высших степеней состоит в следующих шагах:
- Поиск корня n.
- Деление решения на двучлен x-n.
- Получение уравнения на порядок ниже.
Алгоритм повторяется до тех пор, пока уравнение не станет квадратным. При этом следует помнить, что если корень подходит, то деление в алгоритме будет осуществляться нацело.
Поэтому важным этапом является подбирание корня. Находить же его лучше всего используя схему Горнера.
Доказательство теоремы
Схема Горнера отлично работает в связке с теоремой Безу. Овладев навыками их использования решить уравнение с любым показателем в степени можно довольно быстро и эффективно, без сложных подстановок и выполнения деления в столбик.
Для доказательства теоремы допустим, что при делении многочлена F (x) на линейный двучлен икс минус числовой коэффициент, остаток от операции будет равняться величине многочлена в точке, то есть F (n). Разделим многочлен F (x) на (x-n). В результате образуется остаток, равняющийся r.
Деление можно представить, как произведение: F (x) = (x-n) * Q (x). В этом выражении Q (x) будет являться всё так же многочленом, но уже на один степенной порядок ниже, чем F (x). Теперь можно вместо икса подставить числовой коэффициента, то есть использовать что икс равняется эн. Тогда: F (n) = (n-n) * Q (n) + r = r. При этом r является константой. В результате можно утверждать: r = f (n), что и необходимо было доказать.
Для того чтобы быстро определить корни, в доказательстве теоремы Безу используется схема Горнера. Алгоритм используется, когда частное равняется двучлену x — n. Суть его заключается в следующем. Если допустить, что P (x) = a0x n + a1x n-1 + … + a0 в отношении с Q (x) = bn-1 * x n-1 + bn-2 * x n-2 + … + b0 является числителем, то после подстановки выражений в дробь получится равенство: a0x n + a1x n-1 + … + a0 = (bn-1 * x n-1 + bn-2 * x n-2 + … + b0) * (x — a) + r, где свободный член остаток.
Для дальнейшего решения нужно раскрыть скобки и приравнять коэффициенты с одинаковыми показателями в степени. Затем выразить коэффициенты частного через числитель и знаменатель. То есть, an = bn-1; an-1 = bn-2 — a * bn-1; a0 = r -abo. Полученные результаты для наглядности, удобнее заносить в таблицу. Составляется она по следующему принципу:
- начиная со второго столбца первой строчки, записывают коэффициенты из начального уравнения;
- в первый столбик переносят то число, на которое будет выполняться деление, то есть потенциальные корни (х0);
- ниже заносится то, что стоит в верхнем элементе второго столбика;
- для заполнения следующей ячейки нужно выполнить операцию произведения числа на выбранное x0 и прибавить стоящее число, расположенное в столбике сверху;
- проделать аналогичные операции до окончательного заполнения всех ячеек.
Строки, которые в последнем столбике будут равняться нулю и есть искомое решение уравнения. При этом самый последний коэффициент есть остаток, а все предыдущие — коэффициенты неполного частного.
Примеры решения
Теорема Безу применяется при решении степенных уравнений. Согласно её объяснению чтобы понять, чему будет равняться остаток от деления многочлена на двучлен, не нужно выполнять сложные утомительные действия. Достаточно просто подставить число в многочлен. Его значение как раз и будет являться искомым остатком от деления. Но чаще всего при решении задач используется не сама теорема, а следствие из неё — разложение многочленов на множители.
Пусть есть многочлен с целыми коэффициентами: x3 — 5x — 2x + 24. Свободным числом в формуле является двадцать четыре. Его нужно разложить на множители: 24 = 6 * 4 = 2 * 3 * 2 * 2 * 1. Единицу дописывают с целью поиска дополнительных корней. Для того чтобы разложить многочлен на множители нужно вспомнить начальную алгебру. Из неё известно, что если число x1 является корнем какого-либо многочлена P (x), то это выражение можно переписать в виде произведения: P (x) = (x — x1) *Q (x) где степень Q (x) меньше исходной формулы.
Так как у многочлена присутствует некий корень х1, то он обязательно будет делителем числа 24. Следовательно, собираться из множителей числа. Для этого нужно взять наименьшее число, подставив его в исходное выражение и проверить, является ли оно корнем. Тут стоит отметить, что для уравнений сложного вида можно использовать схему Горнера.
Для рассматриваемого примера первое число будет единица. Подставив его в многочлен вместо икса, получим: P (1) = 1 — 5 — 2 + 24 = 18. Ответ не равняется нулю, поэтому единица не будет корнем.
Теперь нужно подставить второй член разложения, цифру два: P (2) = 8 — 20 — 4 + 24 = 8. Ответ снова не подходит. Используем: x = -2: P (-2) = -8 — 20 + 4+ 24 =0. Результат означает, что x = -2 является корнем рассматриваемого многочлена.
Получив корень можно записать: P (x) = (x +2) * Q (x). Осталось найти Q (x). Для этого исходный многочлен нужно разделить на x +2. После деления получится квадратное уравнение вида: х2 — 7x + 12. Таким образом, исходное уравнение можно переписать как P (x) = (x + 2) * (x2 — 7x + 12) = (x + 2) + (x — 3) * (x — 4). Это и есть полное разложение многочлена на линейные множители. При этом корнями уравнения будут: x1 =- 2, x2 =3, x3 = 4.
Применение онлайн-калькулятора
Как бы ни облегчала расчёт теорема всё равно приходится выполнять определённые арифметические действия. Когда уравнение до четвёртого порядка, выполнить операции несложно и самостоятельно. Но чем больше показатель в формуле, тем сложнее выполнять вычисления и больше возникает вероятность допущения ошибки. При этом затрачивается и много времени.
Поэтому резонно для сложных заданий использовать автоматически расчёт уравнений. Выполнить его можно используя любой специализированный сервис — онлайн калькулятор. Теорема Безу предлагает алгоритм расчётов, который запрограммирован в исполняющем приложении. Доступ к интернет-порталам предлагающих такого рода услугу бесплатен. При этом от пользователя не требуется даже регистрации или указания какой-либо информации.
Необходимо просто зайти на страничку онлайн-калькулятора и ввести в предложенную сайтом форму исследуемое уравнение, а после запустить программу нажатием одной кнопки, например, «Рассчитать». Нет необходимости в скачивании или установки программ. Система сама выполнит все вычисления и выдаст ответ. Только в сети рунета существует несколько десятков таких расчётчиков. Из популярных среди пользователей можно выделить следующие:
- Math-solution. Основу сайта составляют различные приложения выполняющие вычисления. Кроме непосредственно решения, сервис предоставляет поэтапное описание действий. Подробное решение излагается в соответствии с принятой программой обучения в школе и вузах. Кроме этого, на сайте существует раздел «Книги». В нём каждый желающий сможет найти учебники, решебники и другую справочную информацию по математике или геометрии.
- Planetcalc. Этот сервис позволит вычислить ответ любой сложности соотношения многочленов. Особенностью его является простой интерфейс, не содержащий загромождения информации. Кроме этого, предложенный поэтапный расчёт сопровождается лаконичными объяснениями.
- Calc. Онлайн-калькулятор имеет интуитивно понятный интерфейс и всю необходимую теорию для понятия теоремы и возможностей её использования. На страничках сайта представлены примеры решений задач различной сложности с подробным описанием действий.
Решив несколько примеров с помощью онлайн-решателей, пользователь сможет самостоятельно научиться применять правила. Автоматические вычислители смогут как подтянуть знания, так и проверить выполненный расчёт.
Ведь возникновение ошибки при использовании приложения практически невозможно.
Алгебра и начало анализа. Теорема Безу. 11-й класс
Класс: 11
Презентация к уроку
Цель урока:
- способствовать развитию навыков деления многочлена на многочлен и использованию схемы Горнера;
- закрепить навыки работы в электронных таблицах OpenOffice.org Calc;
- организовать деятельность учащихся по восприятию, осмысливанию и первичному запоминанию новых знаний;
- разобрать и доказать теорему Безу при решении проблемной ситуации: можно ли разложить многочлен третьей степени на множители;
- рассмотреть использование теорему Безу для решения уравнений высших степеней;
- содействовать развитию логического мышления, внимания, речи и умения работать самостоятельно.
Тип урока: урок ознакомления с новым материалом.
Оборудование: мультимедиа проектор, презентация к уроку, компьютерный класс.
«Для того, чтобы совершенствовать ум, надо больше рассуждать, чем заучивать».
Декарт (1596 -1650). Французский математик, физик, филолог, философ.
Ход урока
I. Организационный момент
Наша задача сегодня в совместной деятельности подтвердить слова Декарта (слайд 1). Тема нашего урока (слайд 2) «Теорема Безу» настолько значима, что даже используется в заданиях ЕГЭ и различных олимпиадах. Теорема Безу облегчает решение многих заданий, содержащих уравнения высших степеней. К сожалению, она изучается только на профильном уровне.
II. Возникновение проблемной ситуации
На этом уроке мы научимся решать уравнения высших степеней, а алгоритм решения выведем сами.
Решить уравнение: x 3 — 2x 2 — 6x + 4=0 (Слайд 3). Возникает проблема: Мы понимаем, что было бы удобно представить левую часть уравнения в виде произведения, и так как произведение равно нулю, то приравнять к нулю каждый множитель. Для этого надо разложить многочлен 3-ей степени на множители. Но как? Можно ли сгруппировать или вынести общий множитель за скобку в нашем случае? (Нет).
III. Актуализация опорных знаний
Вспомним, как разложить на множители многочлен х 2 — 5х — 6? (Слайд 4).
(По формуле разложения на множители квадратного трехчлена:
ах 2 + bх + с = a(x – x1)(x-x2), где х1 и х2 корни трехчлена).
Найдите корни трехчлена двумя способами. Какими?
(по формуле корней квадратного уравнения и по теореме Виета).
Решают на доске от каждой группы по одному ученику. Остальные учащиеся в тетрадях. Получили: х 2 — 5х — 6 = (х — 6) (х + 1).
Это значит, что трехчлен делится на каждый из двучленов: х – 6 и х + 1.
Обратите внимание на свободный член нашего трехчлена и найдите его делители (±1, ±2, ±3, ±6).
Какие из делителей являются корнями трехчлена? (-1 и 6)
Какой вывод можно сделать? (Корни трехчлена являются делителями свободного члена).
IV. Выдвижение гипотезы
Так какой же одночлен поможет подобрать корни многочлена?
Р(х) = x 3 — 2x 2 — 6x + 4=0?
Выпишите его делители: ±1; ±2; ±4.
Найдите значения многочлена для каждого делителя. С помощью электронных таблиц и непосредственно:
http://nauka.club/matematika/teorem%D0%B0-bezu.html
http://urok.1sept.ru/articles/617776