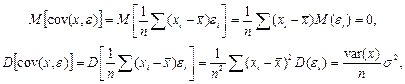Теорема гаусса маркова для уравнения парной регрессии

Предпосылки регрессионного анализа. Условия Гаусса-Маркова

Глава 3. Свойства коэффициентов регрессии и проверка гипотез

Случайные составляющие коэффициентов регрессии

Величина Y в модели регрессии Y = a + b× X + e имеет две составляющие: неслучайную (a + b×X) и случайную (e).

Оценки коэффициентов регрессии (a; b)являются линейными функциями Y и теоретически их также можно представить в виде двух составляющих.

Воспользовавшись разложением показателей:

,

получим преобразованные соотношения для (a; b):

(3.1)

Таким образом, коэффициенты (a; b) разложены на две составляющие:

неслучайную, равную истинным значениям (a; b) и случайную, зависящую от e.

На практике нельзя разложить коэффициенты регрессии на составляющие, т.к. значения (a; b) или фактические значения e в выборке неизвестны.

Предпосылки регрессионного анализа. Условия Гаусса-Маркова

Линейная регрессионная модель с двумя переменными имеет вид:

где Y –объясняемая переменная, X – объясняющая переменная, e – случайный член.

Для того, чтобы регрессионный анализ, основанный на МНК давал наилучшие из всех возможных результаты, должны выполняться условия Гаусса-Маркова.

1.Математическое ожидание случайного члена в любом наблюдении должно быть равно нулю

2. Дисперсия случайного члена должна быть постоянной для всех наблюдений

3. Случайные члены должны быть статистически независимы (некоррелированы) между собой

4.Объясняющая переменнаяx_i естьвеличина неслучайная.

При выполнении условий Гаусса-Маркова модель называется классической нормальной линейной регрессионной моделью.

Наряду с условиями Гаусса-Маркова обычно предполагается, что случайный член распределен нормально, т.е. e_i

Замечание. Если случайный член имеет нормальное распределение, то требование некоррелированности случайных членов эквивалентно их независимости.

Рассмотрим подробнее условия и предположения, лежащие в основе регрессионного анализа.

Первое условие означает, что случайный член не должен иметь систематического смещения. Если постоянный член включен в уравнение регрессии, то это условие автоматически выполняется.

Второе условиеозначает, что дисперсия случайного члена в каждом наблюдении имеет только одно значение.

Под дисперсией s 2 имеется в виду возможное поведение случайного члена до того, как сделана выборка. Величина s 2 неизвестна, и одна из задач регрессионного анализа состоит в её оценке.

Условие независимости дисперсии случайного члена от номера наблюдения называется гомоскедастичностью (что означает одинаковый разброс). Зависимость дисперсии случайного члена от номера наблюдения называется гетероскедастичностью.

Характерные диаграммы рассеяния для двух случаев показаны на рис. 9,а и б соответственно.

Если условие гомоскедастичности не выполняется, то оценки коэффициентов регрессии будут неэффективными, хотя и несмещенными.

Существуют специальные методы диагностирования и устранения гетероскедастичности.

Третье условиеуказывает на некоррелированность случайных членов для каждых двух соседних наблюдений. Это условие часто нарушается, когда данные являются временными рядами. В случае, когда третье условие не выполняется, говорят об автокорреляции остатков.

Типичный вид данных при наличии автокорреляции показан на рис. 10.

Если условие независимости случайных членов не выполняется, то оценки коэффициентов регрессии, полученные по МНК, оказываются неэффективными,хотя и несмещенными.

Существуют методы диагностирования и устранения автокорреляции.

Четвертое условиео неслучайностиобъясняющей переменной является особенно важным.

Если это условие нарушается, то оценки коэффициентов регрессии оказываются смещенными и несостоятельными.

Нарушение этого условие может быть связано с ошибками измерения объясняющих переменных или с использованием лаговых переменных.

В регрессионном анализе часто вместо условия о неслучайности объясняющей переменной используется более слабое условие о независимости (некоррелированности) распределений объясняющей переменной и случайного члена.Получаемые при этом оценки коэффициентов регрессии обладают теми же основными свойствами, что и оценки, полученные при использовании условия о неслучайности объясняющей переменной.

Предположение о нормальности распределения случайного члена необходимо для проверки значимости параметров регрессии и для их интервального оценивания.

Теорема Гаусса-Маркова

Теорема Гаусса-Маркова. Если условия 1-4 регрессионного анализа выполняются, то оценки (a, b), сделанные с помощью МНК, являются наилучшими линейными несмещенными оценками, т.е. обладают следующими свойствами:

несмещенности: M(a) = a, M(b) = b, что означает отсутствие систематической ошибки в положении линии регрессии;

эффективности: имеют наименьшую дисперсию в классе всех линейных несмещенных оценок, равную

;

состоятельности: , что означает, что при достаточно большом n оценки (a; b) близки к (a; b).

Для проверки выводов теоремы воспользуемся оценками (a, b) в виде разложения (3.1) и соотношением

.

Пусть x не случайная величина, тогда

Вычислим математическое ожидание и дисперсию оценок b, a:

Теорема Гаусса-Маркова

Вы будете перенаправлены на Автор24

Понятие эконометрики

Эконометрика – это наука, которая изучает взаимосвязи между экономическими величинами, используя инструменты математики и статистики.

Эконометрика имеет два направления:

1. Теоретическая эконометрика исследует свойства испытаний и оценок, полученных с использованием методов статистики.
2. Прикладная эконометрика изучает применение методов науки для оценки и практической эксплуатации теоретических гипотез.

Это научное направление занимается процессами и явлениями в макро- и микроэкономических системах, создает методологию для их исследования и измерения. Эконометрика так же активно применяется для планирования и прогнозирования будущего состояния экономической системы, в том числе предприятия. В настоящее время эконометрика является частью экономической теории.

Многие университеты мира преподают эконометрику, как науку, выводящую анализ хозяйственных систем на принципиально новый уровень. В России до недавнего времени по объективным причинам эта наука была плохо развита. Однако, в последние годы появились соответствующие научные журналы, статьи и разработки в этой области научного знания. Эконометрика не стоит на месте, очень популярным стало использование непараметрической эконометрики, которая не требует специализировать исследуемые объекты. Она позволяет строить более гибкие модели исследования.

Метод наименьших квадратов

Экономические модели часто содержат элементы, которые не только имеют количественные и качественные характеристик, но и несут смысловую нагрузку, часто имеют размер, что оказывает воздействие на все свойства объекта. Примером из практики может быть анализ зависимости между увеличением расходов и изменением уровня личного дохода домашнего хозяйства.

В основе теоремы Гаусса-Маркова лежит метод наименьших квадратов. Теорема названа в честь двух ученых, которые не пересекались при жизни. Однако, Гаусс смог применить метод наименьших квадратов, а Марков сформулировал условия, при которых этот метод смог дать состоятельную оценку.

Готовые работы на аналогичную тему

Метод наименьших квадратов помогает изучать линейные параметры в эконометрических моделях. Этот метод получил название из-за того, что сумма квадратов ошибки в нем должна быть минимальной. С его помощью минимизируются отклонения функций от исследуемых переменных. Метод наименьших квадратов часто применяется для регрессионного анализа, то есть исследования таких явлений, где совокупность параметров оказывают воздействие на какую-либо величину.

Теорема Гаусса-Маркова

В теореме Гаусса-Маркова рассматривается зависимость параметров X и Y, при соблюдении следующих условий:

1. Модель специфицирована, то есть в ней есть фиксированная и случайная часть. Модель линейна, а неопределенность в ней отсутствует.
2. Все величины Х не равны между собой и не являются постоянными.
3. Каждый член регрессии испытывает отклонения, которые не носят систематического характера.
4. Разброс ошибок всегда одинаковый.
5. Связь между значениями параметра в любых двух ситуациях отсутствует.

Если соблюсти все вышеперечисленные условия, тогда метод наименьших квадратов даст оптимальный результат. Эффективность оценки будет зависеть от размера ее дисперсии, чем меньше дисперсия, тем выше эффективность. Оценка линейна к изменению Y. Если оценка не смещена, то ее математическое значения равно истинному.

Метод наименьших квадратов позволяет добиться наименьшего отклонения от заданной величины. Однако, достижение максимально точного результата возможно только при соблюдении условий, сформулированных в теореме Гаусса-Маркова. В этом случае, случайные возмущения дадут необходимые свойства модели.

Эконометрика: Парная и множественная регрессия (стр. 3 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11

Условия Гаусса–Маркова для модели парной регрессии:

1) случайный член регрессии в каждом наблюдении имеет нулевое математическое ожидание: , для любого i;

2) дисперсия случайного члена регрессии не зависит от номера наблюдения i;

3) случайные члены регрессии в разных наблюдениях не зависят друг от друга, то есть если i¹j;

4) случайный член регрессии и объясняющая переменная в каждом наблюдении независимы друг от друга, то есть для любого i.

Рассмотрим теперь эти условия более подробно.

1-е условие Гаусса–Маркова: , для любого i.

Иногда случайный член будет положительным, иногда отрицательным, но он не должен иметь систематическое смещение ни в одном из двух возможных направлений. Фактически, если уравнение регрессии включает постоянный член, то обычно бывает разумно предположить, что это условие выполняется автоматически, так как роль константы состоит в определении любой систематической тенденции в у, которую не учитывают объясняющие переменные, включенные в уравнение регрессии.

2-е условие Гаусса–Маркова: постоянна для всех наблюдений.

Иногда случайный член будет больше, иногда меньше, однако не должно быть априорной причины для того, чтобы он порождал большую ошибку в одних наблюдениях, чем в других.

Данное условие можно записать в виде , для всех i.

Так как , то данное условие можно переписать в виде , для всех i.

Величина , конечно, неизвестна, поэтому одна из задач регрессионного анализа состоит в оценке стандартного отклонения случайного члена. Если рассматриваемое условие не выполняется, то коэффициенты регрессии, найденные по обычному методу наименьших квадратов, будут неэффективными, а эффект, который при этом получается называется гетероскедастичностью . В этом случае можно получить более надежные результаты путем применения модифицированного метода наименьших квадратов.

3-е условие Гаусса–Маркова: если i¹j.

Это условие предполагает отсутствие систематической связи между значениями случайного члена в двух любых наблюдениях. Например, если случайный член велик и положителен в одном наблюдении, это не должно обусловливать систематическую тенденцию к тому, что он будет большим и положительным в следующем наблюдении (или большим и отрицательным, или малым и положительным, или малым и отрицательным). Случайные члены должны быть абсолютно независимы друг от друга.

В силу того, что , данное условие можно записать следующим образом:

.

Если это условие не будет выполнено, то регрессия, оцененная по обычному методу наименьших квадратов, вновь даст неэффективные результаты, а эффект, вызванный нарушением этого условия, называется автокорреляцией.

4-е условие Гаусса–Маркова: для любого i.

Часто используется более сильное предположение о том, что объясняющая переменная не является стохастической, т. е. не имеет случайной составляющей. Значение любой независимой переменной в каждом наблюдении должно считаться экзогенным, то есть полностью определяемым внешними причинами, не учитываемыми в уравнении регрессии.

Если это условие выполнено, то теоретическая ковариация между зависимой переменной и случайным членом равна нулю. Так как , то

.

Следовательно, данное условие можно записать также в виде: .

Наряду с условиями Гаусса–Маркова обычно также предполагается нормальность распределения случайного члена. Если случайный член u нормально распределен, то также будут распределены коэффициенты регрессии a и b.

Теорема

Если выполнены условия Гаусса–Маркова для модели парной регрессии, то МНК дает несмещенные, эффективные и состоятельные оценки параметров регрессии а и b.

При невыполнении предположений 1) и 4) нарушается свойство несмещенности. Если предположения 2) и 3) нарушены (т. е. дисперсия возмущений непостоянна и/или значения связаны друг с другом), то нарушается свойство эффективности.

Докажем, что b будет несмещенной оценкой b. Из (3.1) следует, что

.

Если использовать 4-е условие Гаусса–Маркова и предположим, что x — неслучайная величина, то можем считать известной константой и , следовательно

Таким образом, b – несмещенная оценка b. Можно получить тот же результат со слабой формой 4-го условия Гаусса–Маркова (которая допускает, что переменная x имеет случайную ошибку, но предполагает, что она распределена независимо от u).

За исключением того случая, когда случайные факторы в n наблюдениях в точности “гасят” друг друга, что может произойти лишь при случайном совпадении, b будет отличаться от b в каждой конкретной выборке. Несмещенность можно доказать и для коэффициента а.

Коэффициент регрессии a можно найти по формуле (2.6), которая имеет вид:

При выполнении 4-го условия Гаусса–Маркова, при котором , будет

.

Поскольку y определяется моделью парной регрессии (2.1), и если предположить, что выполнено 1-е условие Гаусса–Маркова, т. е. , то

.

Если перейти к средним значениям будет, то

Получим: .

Таким образом, а и b – несмещенные оценки параметров a и b при выполнения 1-го и 4-го условий Гаусса–Маркова. Безусловно, для каждой конкретной выборки фактор случайности приведет к расхождению оценки и истинного значения.

Можно доказать, что оценки a и b, полученные методом наименьших квадратов, являются состоятельными и эффективными. Условие состоятельности будет следовать непосредственно из вида стандартных отклонений, а доказательство условия эффективности более трудоемко, поэтому проводиться нами не будем.

Ранее рассматривали оценки математического ожидания m случайной величины x по данным выборочных наблюдений. Хотя использовалось выборочное среднее , было показано, что оно является лишь одной из возможных несмещенных оценок этого параметра. Причина предпочтения выборочного среднего всем другим оценкам состоит в том, что при определенных предположениях оно является состоятельной и эффективной оценкой.

Аналогичные рассуждения применимы и к коэффициентам регрессии. Можно провести прямую линию, черед два произвольных наблюдения и посмотреть, будут ли коэффициенты данной линии несмещенными оценками параметров модели. Возьмем первое и последнее наблюдение, тогда уравнение прямой будет иметь вид:

.

Выразив y, получаем уравнение

. (3.2)

Каковы свойства коэффициентов этого уравнения? Сначала мы исследуем, является ли оценка несмещённой. Имеем

Если выполняется первое условие Гаусса–Маркова, т. е. , то эта, на первый взгляд, “наивна” оценка является несмещенной. Аналогично, можно показать, что и оценка также является несмещенной оценкой для коэффициента a. Доказать данное утверждение несложно, поэтому можно провести его самостоятельно.

Это, разумеется, не единственная оценка, которая наряду с оценкой, полученной методом МНК, обладает свойством несмещенности. Можно получить сколько угодно оценок такого типа путем объединения двух или большего количества произвольно выбранных наблюдений. При этом, для их несмещенности достаточно потребовать выполнение первого условия Гаусса–Маркова.

При сравнении с менее “наивными” оценками превосходство оценки МНК в эффективности может быть не столь очевидным. Тем не менее, в том случае, если условия Гаусса–Маркова для остаточного члена выполнены, коэффициенты регрессии, построенной обычным методом наименьших квадратов, будут наилучшими линейными несмещенными оценками (best linear unbiased estimators, или BLUE).

3.2. Стандартные отклонения и стандартные ошибки коэффициентов регрессии

Рассмотрим теперь теоретические дисперсии оценок а и b. Они задаются следующими выражениями

, (3.3)

. (3.4)

Из уравнений можно сделать три очевидных заключения.

1. Данные оценки являются состоятельными. Поскольку значение n находится в знаменателе, то дисперсии стремятся к нулю, при увеличении числа элементов в выборке.

2. Дисперсии a и b прямо пропорциональны дисперсии остаточного члена . Чем больше фактор случайности, тем хуже будут оценки при прочих равных условиях.

3. Чем больше дисперсия x, тем меньше будет дисперсия коэффициентов регрессии. В чем причина этого? Коэффициенты регрессии вычисляются на основании предположения, что наблюдаемые изменения y происходят вследствие изменений x, но в действительности они лишь отчасти вызваны изменениями x, а отчасти вариациями u. Чем меньше дисперсия x, тем больше будет влияние случайного фактора при определении отклонений y. В действительности важнее не абсолютные значения величин и , а их отношение.

На практике, как правило, нельзя вычислить теоретические дисперсии a или b, так как дисперсия случайного члена модели регрессии неизвестна. Однако можно получить оценку на основе остатков. Выборочная дисперсия остатков , которую мы можем измерить, сможет быть использована для оценки , которая имеет тенденцию занижать . Действительно, можно показать, что математическое ожидание , если имеется всего одна независимая переменная, будет

.

Следовательно, , будет несмещенной оценкой .

Если рассматривать не дисперсии, а суммы квадратов отклонений, то несмещенной оценкой параметра регрессии является оценка , где ESS – необъясненная сумма квадратов отклонений.

Поскольку имеется дисперсии коэффициентов регрессии (3и оценки данных значений, необходимо разделять данные понятия, следовательно, необходимы следующие определения:

стандартное отклонение случайной величины – корень квадратный из дисперсии случайной величины;

стандартная ошибка случайной величины – оценка стандартного отклонения случайной величины, полученная по данным выборки. Стандартная ошибка функции коэффициента регрессии будем обозначать в виде и . Таким образом, для парного регрессионного анализа имеем следующие оценки дисперсии и стандартные ошибки:

, (3.5)

,

Как правило, при работе в специализированных пакетах, стандартные ошибки (а не стандартные отклонения) будут подсчитаны автоматически одновременно с оценками а и b.

Подводя итог можно заключить:

1. Оценка a для параметра a имеет нормальное распределение с математическим ожидание a и стандартным отклонением ;

2. Оценка b для параметра b имеет нормальное распределение с математическим ожидание b и стандартным отклонением ;

3. На практике, как правило, значение стандартного отклонения подсчитать невозможно, поэтому необходимо вычислять стандартные ошибками и , используя формулы (3.5) и (3.6).

§ 4. Некоторые распределения

До сих пор мы формально использовали термин нормально распределенная случайная величина. Сейчас рассмотрим основные свойства нормального распределения, а так же рассмотрим некоторые распределения, которые понадобятся для дальнейшего изложения.

4.1. Функция распределения и плотность распределения

Непрерывная случайная величина X может принимать значения из некоторого интервала. Вероятность того, что X примет значение, меньшее вещественного x, называется функция распределения случайной величины и определятся следующим образом . Иногда данную функцию называют интегральной функцией распределения.

В теории вероятностей принято обозначить случайные величины прописными (заглавными) буквами. Именно такое обозначение будет использоваться в данном параграфе.

Функция распределения для непрерывной случайной величины везде непрерывна, является неубывающей функций, при этом

При помощи функции распределения можно определить вероятность того, что случайная величина попадет в некоторый полуоткрытый полуинтервал.

Вычислим вероятность попадания случайной величины в некоторый малый интервал . Рассмотрим отношения этой вероятности к длине этого участка. Устремив к нулю, в пределе получим функцию производную от функции распределения

Функция f(x) называется плотностью распределения случайной величины (дифференциальной функцией распределения).

Плотность распределения является неотрицательной функцией, вследствие неубывания функции распределения и интеграл от минус до плюс бесконечности от функции плотности равняется 1:

Вероятность попадания случайной величины в заданный интервал через плотность распределения: .

4.2. Нормальное распределение

Плотность вероятности нормально распределенной случайной величины на интервале (-¥, +¥) задается формулой:

, (4.1)

а функция распределения

. (4.2)

Основные характеристики данного распределения имеют следующие значения , . Обычно нормально распределенная случайная величина обозначается следующим образом: .

График плотности вероятности нормального распределения имеет колоколообразный вид (рис. 5). Максимум этой функции находится в точке m ,растянутость вдоль оси y определяется параметром s. Чем меньше значение этого параметра, тем более острый и высокий максимум имеет плотность нормального распределения. Максимум данной функции достигается в точке с координатами .

Если случайная величина формируется под действием большого количества независимых факторов, вклад каждого из которых в значение случайной величины мал, то в силу центральной предельной теоремы эта случайная величина будет иметь нормальное распределение. В роли таких величин в экономике могут выступать: объем продаж, суммарные инвестиции, суммарное потребление домашних хозяйств и тому подобные величины, имеющие аддитивную природу, то есть складывающиеся из многих малых взаимно независимых величин.

Рассмотрим основные свойства нормального распределения. Главное из них – если ряд случайных величин имеет нормальное распределение, то их сумма или любая линейная комбинация также будет иметь нормальное распределение.

Распределение величины , представляющей собой взвешенную сумму n независимых нормально распределенных случайных величин с параметрами и , также будет иметь нормальное распределение с параметрами и . В частности, если все , все и одинаковы, то случайная величина имеет следующие характеристики: , .

Подобная случайная величина нами уже изучалась ранее. Данная величина называется выборочное среднее.

Плотность вероятности нормального распределения (4.1) пропорциональна безразмерной величине, , где z – определяемая выражением . Поэтому плотность нормального распределения экспоненциально убывает при удалении от среднего значения m. Случайная величина z имеет нулевое математическое ожидание и единичную дисперсию. Она, как и исходная случайная величина x, нормально распределена, но не зависит от каких-либо параметров. Поэтому ее распределение может быть протабулировано, то есть значения её плотности вероятности могут быть представлены в виде таблиц. Эта функция называется плотностью стандартного нормального распределения, а сама случайная величина стандартно нормальной и обозначается . На практике чаще используют таблицы значений функции распределения стандартной нормальной величины (приложение 1).

Операцией нормализации называется переход от произвольной случайной величины X к величине Z, определенной по правилу .