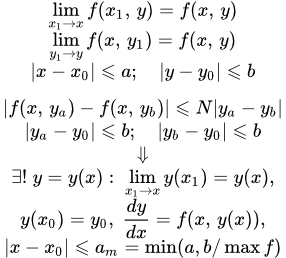Теорема коши для дифференциального уравнения 1 порядка

Теорема коши для дифференциального уравнения 1 порядка

Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах…
Часть II. Глава IV. Обыкновенные дифференциальные уравнения

§ 1. Дифференциальные уравнения первого порядка

1. Основные понятия. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функцию и производные (или дифференциалы) этой функции. Если независимая переменная одна, то уравнение называется обыкновенным; если же независимых переменных две или больше, то уравнение называется дифференциальным уравнением в частных производных.

Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Например:

1) х²у’ + 5xy = у² – обыкновенное дифференциальное уравнение первого порядка;

2) – обыкновенное дифференциальное уравнение второго порядка;

3) y’³ + y»y»’ = х – обыкновенное дифференциальное уравнение третьего порядка;

4) F (х, у, у’, у») = 0 – общий вид обыкновенного дифференциального уравнения второго порядка;

5) – уравнение в частных производных первого порядка.

В этом параграфе рассматриваются обыкновенные дифференциальные уравнения первого порядка, т. е. уравнения вида F (х, у, у’) = 0 или (в разрешенном относительно у’ виде) y’ = f(х, у).

Решением дифференциального уравнения называется такая дифференцируемая функция у = φ (x), которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения.

Общим решением дифференциального уравнения первого порядка у’ = f(x, у) в области D называется функция у = φ(x, C), обладающая следующими свойствами: 1) она является решением данного уравнения при любых значениях произвольной постоянной С, принадлежащих некоторому множеству; 2) для любого начального условия у(х0) = у0 такого, что (x0; y0) ∈ 0, существует единственное значение С = С0, при котором решение у = φ(x, C0) удовлетворяет заданному начальному условию.

Всякое решение у = φ(x, C0), получающееся из общего решения у = φ (x, C) при конкретном значении С = С0, называется частным решением.

Задача, в которой требуется найти частное решение уравнения y’ = f(х, у) удовлетворяющее начальному условию у(х0) = y0, называется задачей Коши.

Построенный на плоскости хОу график всякого решения у = φ(х) дифференциального уравнения называется интегральной кривой этого уравнения. Таким образом, общему решению у = φ(х, С) на плоскости хОу соответствует семейство интегральных кривых, зависящее от одного параметра – произвольной постоянной С, а частному решению, удовлетворяющему начальному условию y(x0) = y0, – кривая этого семейства, проходящая через заданную точку М0(x0; у0).

Если функция f(х, у) непрерывна и имеет непрерывную производную в области D, то решение дифференциального уравнения у’= f (х, у) при начальном условии у(х0) = у0 существует и единственно, т. е. через точку (x0; y0) проходит единственная интегральная кривая данного уравнения (теорема Коши).

Особым решением называется такое решение, во всех точках которого условие единственности не выполняется, т. е. в любой окрестности каждой точки (х; у) особого решения существуют по крайней мере две интегральные кривые, проходящие через эту точку.

Особые решения не получаются из общего решения дифференциального управления ни при каких значениях произвольной постоянной С (в том числе и при С = ± ∞).

Особым решением является огибающая семейства интегральных кривых (если она существует), т. е. линия, которая в каждой своей точке касается по меньшей мере одной интегральной кривой.

Например, общее решение уравнения записывается в виде у = sin (х + С). Это семейство интегральных кривых имеет две огибающие: у = 1 и у = -1, которые и будут особыми решениями.

2. Дифференциальные уравнения с разделяющимися переменными. Дифференциальное уравнение вида

относится к типу уравнений с разделяющимися переменными. Если ни одна из функций f1(x), f2(y), φ1(x), φ2(y) не равна тождественно нулю, то в результате деления исходного уравнения на f2 (x) φ1 (y) оно приводится к виду

Почленное интегрирование последнего уравнения приводит к соотношению

которое и определяет (в неявной форме) решение исходного уравнения. (Решение дифференциального уравнения, выраженное в неявной форме, называют интегралом этого уравнения.)

507. Решить уравнение х(у²-4)dx + y dy = 0.

△ Разделив обе части уравнения на у² – 4 ≠ 0, имеем

x² + ln|у² – 4| = ln|C|, или у² – 4 = Сe -λ²

Это общее решение данного дифференциального уравнения.

Пусть теперь у² – 4 = 0, т. е. у = ± 2. Непосредственной подстановкой убеждаемся, что у = ±2 – решение исходного уравнения. Но оно не будет особым решением, так как его можно получить из общего решения при С = 0. ▲

508. Найти частный интеграл уравнения у’ cos х = у / ln у, удовлетворяющий начальному условию y(0) = l.

△ Полагая , перепишем данное уравнение в виде

Проинтегрируем обе части уравнения:

, или

Используя начальное условие у = 1 при х = 0, находим С = 0. Окончательно получаем

▲

509. Найти общий интеграл уравнения у’ = tg x tg y.

△ Полагая и разделяя переменные, приходим к уравнению ctg у dy = tg х dx. Интегрируя, имеем

, или ln|sin у| = -ln|cos x| + ln С.

Отсюда находим sin y = C/cos x, или sin y / cos x = С (общий интеграл). ▲

510. Найти частное решение дифференциального уравнения (l + x²)dy + y dx = 0 при начальном условии у(1) = 1.

△ Преобразуем данное уравнение к виду . Интегрируя, получим

, или ln |y| = – arctg x + С

Это и есть общий интеграл данного уравнения.

Теперь, используя начальное условие, найдем произвольную постоянную С; имеем ln 1 = — arctg 1 + С, т. е. С = π/4. Следовательно,

ln у = – arctg х + π/4,

откуда получаем искомое частное решение y = e π/4 – arctg x . ▲

Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах… Ч. II. Стр. 117-119.

Теорема Коши существования и единственности решения дифференциального уравнения первого порядка

Впервые существование решения дифференциального уравнения было доказано Коши. Приводимое ниже доказательство основано на методе последовательных приближений, который принадлежит Пикару. Этот метод имеет самостоятельное значение, поскольку позволяет получить приближенное решение дифференциального уравнения.

Формулировка теоремы

Пусть дано дифференциальное уравнение первого порядка:
(1)
с начальным условием
(1.1) .
Пусть – непрерывная функция двух переменных в замкнутой области :

и, следовательно, ограничена некоторым положительным значением :
(2) .
И пусть функция удовлетворяет условию Липшица:
(3) ,
.
Тогда существует единственное решение уравнения (1):
,
удовлетворяющее начальному условию , определенное и непрерывное для значений в интервале:
,
где есть наименьшее из двух чисел и .

Условие Липшица

Рассмотрим условие Липшица. Оно имеет вид:
(3) ,
где – положительное число;
, и – любые значения из области :
, , .

Смысл условия Липшица легко понять, если записать его в виде:
(3.1) .
При некотором фиксированном значении переменной , функция является функцией от переменной : . Пусть мы имеем график этой функции. Возьмем две точки, принадлежащие , на этом графике и проведем через них прямую. Тогда угол между прямой и осью ограничен некоторым значением , которое меньше . При таком ограничении график не имеет вертикальных касательных и скачков. А в тех точках, где существует частная производная , она ограничена:
.

Если в области функция имеет непрерывную частную производную , то в этой области выполняется условие Липшица (3).
Для доказательства заметим, что поскольку частная производная непрерывна в замкнутой области, то она ограничена:
.
По теореме Лагранжа о конечных приращениях, имеем:
,
где частные производные вычисляются в некоторой точке , в которой переменная принадлежат интервалу между и :
.
Тогда:
.

Доказательство существования решения

Приведем исходное уравнение (1) с начальным условием (1.1) к интегральному уравнению. Левая и правая части (1) являются функциями от . Заменим на :
.
Интегрируем это уравнение по от до :
;
Подставим начальное условие . В результате получим интегральное уравнение:
(4) .

Покажем, что интегральное уравнение (4) эквивалентно дифференциальному уравнению (1) с начальным условием (1.1). Для этого нужно показать, что из (1) и (1.1) следует (4) и из (4) следует (1) и (1.1). То, что из (1) и (1.1) следует (4) мы уже показали. Осталось показать, что из (4) следует (1) и (1.1). Для этого подставим в (4) . Получим начальное условие (1.1). Продифференцировав обе части уравнения (4) по , получаем уравнение (1).

Далее мы пытаемся найти решение уравнения (4) с помощью последовательных приближений. Для этого определяем ряд функций от переменной по формулам:
(5.1) ;
(5.2) ;
(5.3) ;
.
(5.n) .
Мы предполагаем, что при , стремится к решению уравнения (4):
(6) ,
где – решение уравнения (4). Если мы докажем это, то мы докажем существование решения.

Доказательство существования решения будем проводить в два этапа:
1> вначале докажем, что предел (6) существует;
2) затем докажем, что удовлетворяет уравнению (4):
.

1) Доказательство существования предела y_n при n стремящемся к бесконечности

Сведем последовательные приближения (5.1) – (5.n) к сумме ряда. Для этого пишем:

.
Таким образом нам нужно доказать, что ряд
(7)
сходится при .

Сначала покажем, что при , последовательные приближения принадлежат интервалу .
Действительно, при имеем:
.
Поскольку есть наименьшее из двух чисел и , то и
.

Далее, поскольку принадлежит интервалу , то . Тогда, аналогично предыдущему,
.
Отсюда
.

Далее, по индукции, поскольку принадлежат интервалу , то и
.
Отсюда
.

Итак, мы доказали, что последовательные приближения принадлежат интервалу
.
Теперь мы можем оценить члены ряда (7), применяя условие Липшица.

Для первого члена имеем:
;
(8.1) .
Для второго члена применяем условие Липшица и оценку (8.1):

;
(8.2) .
Для третьего члена применяем, аналогично, условие Липшица и оценку (8.2):

;
(8.3) .

Далее применим метод индукции. Пусть
(8.n) .
Тогда

;
(8.n+1) .
Итак, поскольку (8.n) справедливо для и из (8.n) следует (8.n+1), то (8.n) выполняется для любых .

Запишем ряд (7) в виде:
(7.1) ,
где .
Применим (8.n) и заменим наибольшим допустимым значением :
.
Тогда каждый член ряда (7.1) ограничен по модулю членом ряда
(9) .
Исследуем ряд (9) на сходимость. Применим признак Даламбера:
.
Итак, ряд (9) сходится. Поскольку все члены ряда (7.1), начиная со второго, по абсолютной величине меньше членов сходящегося ряда (9), то, в силу критерия Вейерштрасса, ряд (7.1) сходится равномерно для всех , удовлетворяющих условию . Поскольку интеграл есть непрерывная функция от верхнего предела, то каждый член ряда (7.1) есть непрерывная функция от . Поэтому предел
(10)
существует и является непрерывной функцией от .

2) Доказательство того, что Y является решением (4)

Рассмотрим уравнение (5.n):
(5.n) .
Докажем, что при , это уравнение стремится к уравнению
(11) .

В силу (10) левая часть уравнения (5.n) стремится к .

Теперь покажем, что
.

Перепишем правую часть (5.n):
.
Далее заметим, что поскольку все принадлежат закрытому интервалу , то и принадлежит этому интервалу, . Поэтому мы можем применить условие Липшица.

Оценим абсолютную величину последнего члена:

.
Поскольку, при , стремится к равномерно, то для любого положительного числа можно указать такое натуральное число , что для всех ,
.
Тогда
.
Поскольку произвольно, то

Поэтому
.
То есть при уравнение
(5.n)
принимает вид
(11) .

Доказательство единственности решения

Предположим, что уравнение
(4)
имеет два решения и , различающиеся в некоторой точке , принадлежащей интервалу .
Рассмотрим функцию
.
Будем считать, что . В противном случае поменяем местами и .
Поскольку и непрерывны, то и непрерывная функция. Поэтому она отлична от нуля в некотором интервале, содержащем точку :
при .
Поскольку , то . То есть точка не принадлежит этому интервалу.

Если , то преобразуем (4) следующим образом:
,
где
.
Если переобозначить постоянные
,
то получим задачу (4), для которой
;
при ,
где – некоторое число, не превосходящее .

Если , то поступаем аналогично:
,
Переобозначим постоянные:
.
Получаем задачу (4), для которой
;
при ,
где – некоторое число, не меньшее .

Итак, мы имеем:
;
при ( или при ).
Далее возьмем произвольное положительное число ( или ) и рассмотрим закрытый интервал ( или ). Поскольку функция непрерывна, то она достигает наибольшего значения в одной из точек этого интервала:
( или ).

Сделаем оценку, применяя уравнение (4) и условие Липшица:

;
.
Поскольку , то разделим на :
.
Возникает противоречие, поскольку при это неравенство не выполняется.

Следовательно, не может иметь отличных от нуля значений. Поэтому . Что и требовалось доказать.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Автор: Олег Одинцов . Опубликовано: 04-06-2016 Изменено: 20-06-2016

Теорема коши для дифференциального уравнения 1 порядка

где х — независимая переменная; у — искомая функция; у’ — её производная, называется дифференциальным уравнением первого порядка.

Если уравнение (3) можно разрешить относительно у’, то оно принимает вид:

и называется уравнением первого порядка, разрешенным относительно производной.
Будем рассматривать именно такие уравнения.

В некоторых случаях дифференциальное уравнение (4) первого порядка удобно записывать в форме:

где Р(х,у) и Q(x,y) – известные функции. Форма (5) удобна тем, что здесь переменные х и у равноправны, т.е. каждую из них можно рассматривать как функцию другой. Под решениями уравнения (5), в общем случае, понимаются функции x=φ(t), y=ψ(t), заданные параметрически (t – параметр) и удовлетворяющие уравнению (5).

Не существует общего метода интегрирования дифференциального уравнения первого порядка. Обычно рассматривают лишь некоторые отдельные типы таких уравнений, для каждого из них которых дается свой особый способ решения.

Ответ на вопрос о том, при каких условиях уравнение (4) имеет решение, дает теорема Коши, которая называется теоремой о существовании и единственности решения дифференциального уравнения (4) и является основной теоремой в теории дифференциальных уравнений.

ТЕОРЕМА.(теорема Коши). Если функция f(х,y) и ее частная производная f’_y(х,y) определены и непрерывны в некоторой области G плоскости Оху, то какова бы ни была внутренняя точка (x₀,y₀) области G, в некоторой окрестности этой точки существует единственное решение уравнения у’=f(x,у), удовлетворяющее условиям:

Теорема Коши дает возможность по виду дифференциального уравнения (4) решать вопрос о существовании и единственности его решения. Это особенно важно в тех случаях, когда заранее неизвестно, имеет ли данное уравнение решение. Геометрически теорема утверждает, что через каждую внутреннюю точку (x₀,y₀) области G проходит единственная интегральная кривая. Очевидно, что в области G уравнение (4) имеет бесконечное число различных решений.

Условия (6), в силу которых функция у=φ(х) принимает заданное значение у₀ в заданной точке х₀, называют начальными условиями решения и записывают обычно так:

Отыскание решения уравнения (4), удовлетворяющего начальным условиям (7), — одна из важнейших задач теории дифференциальных уравнений. Эта задача называется задачей Коши. С геометрической точки зрения решить задачу Коши — значит из множества интегральных кривых выделить ту, которая проходит через заданную точку (x₀,y₀) плоскости Оху.

Точки плоскости, через которые либо проходит более одной интегральной кривой, либо не проходит ни одной интегральной кривой, называются особыми точками данного уравнения.