Теорема о ненулевых решениях однородной системы линейных уравнений

Определение общего решения СЛУ. Базисные и свободные неизвестные.

Системой уравнений называется общим решением совместная система A1x1+A2x2+…+Anxn=B (1), если выполняется следующее условие:
A1’x1+A2’x2+…+An’xn=B (2)
система (2) общее решение сист. (1)
условия:1)система (1) и (2) должны быть равносильны
2)система векторов A1,A2. An в сист. уравнений (2) явл. Разрешённой системой векторов

Набор неизвестных системы уравнения (1) называются базисными, если векторы при этих неизвестных образуют базис системы A1A2…An
не базисные неизвестные принято называть свободными.

Однородные СЛУ. Свойства однородной СЛУ. Теорема о нулевом и ненулевом решении СЛУ,

Однородная система — система, у которой все свободные члены равны нулю.

Однородная система—всегда совместна, так как x₁=x₂=x₃=. =x_n=0является решением системы.

Теоремы о ненулевых решениях однородной системы :

Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n неизвестных, т. е. r

а) вектора F1,F2..Fk линейно-независимы

б) k=n-r(A) – число решений равно разности количества неизвестных и ранга системы

Теорема об условии существования ФСР однородной СЛУ

Любое линейное однородное дифференциальное уравнение n -го порядка с непрерывными коэффициентами имеет фундаментальную систему решений, т.е. систему из n линейно независимых решений.

53. Однородные системы уравнений

Линейное уравнение называется Однородным, если его свободный член равен нулю, и неоднородным в противном случае. Система, состоящая из однородных уравнений, называется однородной и имеет общий вид:

Очевидно, что всякая однородная система совместна и имеет нулевое (тривиальное) решение. Поэтому применительно к однородным системам линейных уравнений часто приходится искать ответ на вопрос о существовании ненулевых решений. Ответ на этот вопрос можно сформулировать в виде следующей теоремы.

Теорема. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных.

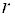
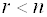
Доказательство: Допустим, система, ранг которой равен, имеет ненулевое решение. Очевидно, что не превосходит . В случае система имеет единственное решение. Поскольку система однородных линейных уравнений всегда имеет нулевое решение, то именно нулевое решение и будет этим единственным решением. Таким образом, ненулевые решения возможны только при .

Следствие 1: Однородная система уравнений, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение.

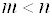
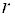
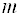
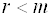
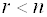
Доказательство: Если у системы уравнений , то ранг системы не превышает числа уравнений , т. е. . Таким образом, выполняется условие и, значит, система имеет ненулевое решение.

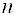
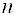
Следствие 2: Однородная система уравнений с неизвестными имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю.

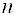
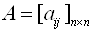
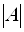
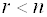
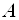
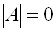
Доказательство: Допустим, система линейных однородных уравнений, матрица которой с определителем , имеет ненулевое решение. Тогда по доказанной теореме , а это значит, что матрица вырожденная, т. е. .

Однородные СЛАУ. Фундаментальная система решений

Однородные СЛАУ

Однородной СЛАУ называется система, все правые части которой равны нулю одновременно.

Однородная СЛАУ, записанная в матричном виде, $A X=\Theta$ всегда совместна, так как $X=\Theta$ всегда является ее решением.

Заметим, что если $x_<1>, x_<2>$ — это два решения однородной СЛАУ, то их линейная комбинация также будет решением однородной СЛАУ:

$$Y=\lambda_ <1>x_<1>+\lambda_ <2>x_<2>$$ $$A Y=A\left(\lambda_ <1>x_<1>+\lambda_ <2>x_<2>\right)=\lambda_ <1>A x_<1>+\lambda_ <2>A x_<2>=\lambda_ <1>\Theta+\lambda_ <2>\Theta=\Theta$$

Если однородная квадратная СЛАУ имеет ненулевое решение, то определитель матрицы системы равен нулю.

Задание. Выяснить, имеет ли однородная СЛАУ $\left\<\begin 3 x-2 y=-1 \\ x+3 y=7 \end\right.$ ненулевые решения.

$$\Delta=\left|\begin 3 & -2 \\ 1 & 3 \end\right|=9-(-2)=9+2=11 \neq 0$$

Так как определитель не равен нулю, то система имеет только нулевое решение $x=y=0$

Ответ. Система имеет только нулевое решение.

Фундаментальная система решений

Рассмотрим множество всех столбцов, которые являются решениями исходной системы.

Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов.

Количество элементов в ФСР равно количеству неизвестных системы минус ранг матрицы системы. Любое решение исходной системы есть линейная комбинация решений ФСР.

Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и общего решения соответствующей однородной СЛАУ.

Задание. Найти общее решение и ФСР однородной системы $\left\<\begin x_<1>+x_<2>-3 x_<4>-x_<5>=0 \\ x_<1>-x_<2>+2 x_<3>-x_<4>=0 \\ 4 x_<1>-2 x_<2>+6 x_<3>+3 x_<4>-4 x_<5>=0 \\ 2 x_<1>+4 x_<2>-2 x_<3>+4 x_<4>-7 x_<5>=0 \end\right.$

Решение. Приведем систему к ступенчатому виду с помощью метода Гаусса. Для этого записываем матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут получаться нули):

$$A=\left(\begin 1 & 1 & 0 & -3 & -1 \\ 1 & -2 & 2 & -1 & 0 \\ 4 & -2 & 6 & 3 & -4 \\ 2 & 4 & -2 & 4 & -7 \end\right)$$

с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем первую, от третьей — четыре первых, от четвертой — две первых:

$$A \sim\left(\begin 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & -6 & 6 & 15 & 0 \\ 0 & 2 & -2 & 10 & -5 \end\right)$$

Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три вторых, к четвертой прибавляем вторую:

$$A \sim\left(\begin 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 9 & -3 \\ 0 & 0 & 0 & 12 & -4 \end\right)$$

От четвертой строки отнимем $\frac<4><3>$ третьей и третью строку умножим на $\frac<1><3>$ :

$$A \sim\left(\begin 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 3 & -1 \\ 0 & 0 & 0 & 0 & 0 \end\right)$$

Нулевые строки можно далее не рассматривать, тогда получаем, что

$$A \sim\left(\begin 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 3 & -1 \end\right)$$

Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а ко второй строке прибавляем третью:

$$A \sim\left(\begin 1 & 1 & 0 & -6 & 0 \\ 0 & -2 & 2 & 5 & 0 \\ 0 & 0 & 0 & 3 & -1 \end\right)$$

то есть получаем систему, соответствующую данной матрице:

Или, выразив одни переменные через другие, будем иметь:

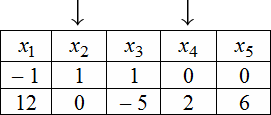
Здесь $x_<2>, x_<4>$ — независимые (или свободные) переменные (это те переменные, через которые мы выражаем остальные переменные), $x_<1>, x_<3>, x_<5>$ — зависимые (связанные) переменные (то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных $n$ (в рассматриваемом примере $n=5$ , так как система зависит от пяти переменных) и ранга матрицы $r$ (в этом случае получили, что $r=3$ — количество ненулевых строк после приведения матрицы к ступенчатому виду): $n-r=5-3=2$

Так как ранг матрицы $r=3$ , а количество неизвестных системы $n=5$ , то тогда количество решений в ФСР $n-r=5-3=2$ (для проверки, это число должно равняться количеству свободных переменных).

Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки). В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:

Тогда придавая в первом случае, например, независимым переменным значения $x_<2>=1$ , $x_<4>=0$ получаем, что $\left\<\begin x_<1>=-1+6 \cdot 0=-1 \\ x_<3>=1-\frac<5> <2>\cdot 0=1 \\ x_<5>=3 \cdot 0=0 \end\right.$ . Полученные значения записываем в первую строку таблицы. Аналогично, беря $x_<2>=0$ , $x_<4>=2$, будем иметь, что =12, x_<3>=-5, x_<5>=6> , что и определяет второе решение ФСР. В итоге получаем следующую таблицу:

Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:

$$X_<1>=\left(\begin -1 \\ 1 \\ 1 \\ 0 \\ 0 \end\right), X_<2>=\left(\begin 12 \\ 0 \\ -5 \\ 2 \\ 6 \end\right)$$

Общее решение является линейной комбинацией частных решений:

$$X=C_ <1>X_<1>+C_ <2>X_<2>=C_<1>\left(\begin -1 \\ 1 \\ 1 \\ 0 \\ 0 \end\right)+C_<2>\left(\begin 12 \\ 0 \\ -5 \\ 2 \\ 6 \end\right)$$

где коэффициенты $C_<1>, C_<2>$ не равны нулю одновременно. Или запишем общее решение в таком виде:

Придавая константам $C_<1>, C_<2>$ определенные значения и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.