Неявные функции
Неявные функции, определяемые одним уравнением.
Пусть функция \(F(x,y)\) определена в \(R^2\). Рассмотрим уравнение
$$
F(x,y)=0.\label
$$
Множество \(G_F\) точек плоскости, координаты которых удовлетворяют уравнению \eqref
Так, график уравнения \(x^2 + y^2 — 1 = 0\) есть окружность, график уравнения \((x-1)(x+y-1)=0\) есть пара прямых \(x = 1\) и \(x+y-1=0\) (рис. 28.1).
Рис. 28.1
Если график \(G_F\) уравнения \eqref
Но, как правило, график уравнения \eqref Рис. 28.2
Меняя местами переменные \(x\) и \(y\), можно говорить о том, что уравнение \eqref
Докажем теорему, дающую достаточные условия существования, непрерывности и дифференцируемости неявной функции, определяемой уравнением \eqref
- функция \(F(x,y)\) имеет в окрестности точки \((x_0,y_0)\) непрерывные частные производные \(F_x(x,y)\) и \(F_y(x,y)\);
- \(F(x_0,y_0)=0\);
- \(F_y(x_0,y_0)\neq 0\).
Тогда существует прямоугольник
$$
K = \<(x,y): \; x_0-a\leq x\leq x_0+a, \; y_0-b\leq y\leq y_0+b\>,\nonumber
$$
в котором уравнение \(F(x,y) = 0\) определяет \(y\) как неявную функцию \(x\). Функция \(y=f(x)\) непрерывно дифференцируема на интервале \((x_0-a,x_0+a)\) и
$$
f'(x)=-\frac
$$
\(\circ\) Разобьем доказательство на два пункта.
Доказательство существования неявной функции. Из условия \(F_y(x_0,y_0)\neq 0\) следует, что либо \(F_y(x_0,y_0) > 0\), либо \(F_y(x_0,y_0) 0.\label
$$
Если \(F_y(x_0,y_0) 0\).
Так как функция \(F_y(x,y)\) в точке \((x_0,y_0)\) непрерывна и в силу условия \eqref
$$
K_1=\<(x,y): \; |x-x_0|\leq a_1, \; |y-y_0|\leq b\>,\nonumber
$$
в котором функция \(F_y(x,y) > 0\).
Рис. 28.3
Рассмотрим функцию одной переменной
$$
\psi (y)=F(x_0,y),\quad y_0-b\leq y\leq y_0+b.\nonumber
$$
Функция \(\psi (y)\) строго возрастает на отрезке \([y_0-b,y_0+b]\), так как
$$
\psi'(y)=F_y(x_0,y) > 0.\nonumber
$$
Кроме того, в силу условия \(F(x_0,y_0)=0\)
$$
\psi (y_0) = F(x_0,y_0) = 0.\nonumber
$$
Поэтому
$$
\psi (y_0-b)= F(x_0,y_0-b) 0.\label
$$
Неравенства \eqref
$$
F(x,y_0-b) 0.\label
$$
Покажем, что в прямоугольнике
$$
K=\<(x,y): \; |x-x_0|\leq a, \; |y-y_0|\leq b\>,\nonumber
$$
уравнение \(F(x,y) = 0\) определяет \(y\) как неявную функцию \(x\).
Возьмем любую точку \(x^*\in [x_0-a,x_0+a]\) и рассмотрим непрерывную на отрезке \([y_0-b,y_0+b]\) функцию одной переменной \(\varphi (y)=F(x^*,y)\). В силу условия \eqref
$$
\varphi(y_0-b)= F(x^*,y_0-b) 0.\nonumber
$$
По теореме Коши о промежуточных значениях найдется такая точка \(y^*\in [y_0-b,y_0+b]\), что
$$
\varphi(y^*) = F(x^*,y^*)=0.\nonumber
$$
Так как \(\varphi'(y) = F_y(x^*,y) > 0\), то функция \(\varphi(y)\) строго возрастает на отрезке \([y_0-b,y_0+b]\) и не может обратиться на этом отрезке в нуль более одного раза.
Таким образом, для любого \(x\in [x_0-a,x_0+a]\) найдется единственный \(y\in [y_0-b,y_0+b]\) такой, что \(F(x,y) = 0\). Это означает, что в прямоугольнике \(K\) уравнение \(F(x,y) = 0\) определяет \(y\) как неявную функцию \(x\).
Доказательство непрерывной дифференцируемости неявной функции. Непрерывная на замкнутом прямоугольнике \(K\) функция \(F_y(x,y)\) по теореме Вейерштрасса принимает на этом прямоугольнике свое наименьшее значение \(\alpha\). Так как \(F_y(x,y) > 0\) на \(K\), то
$$
F_y(x,y)\geq a > 0,\qquad (x,y)\in K.\label
$$
Непрерывная на \(K\) функция \(F_x(x,y)\) ограничена на \(K\). Поэтому
$$
|F_x(x,y)| Замечание 1.
Если известно, что уравнение \(F(x,y)=0\) определяет в прямоугольнике \(a\leq x\leq b, \; c\leq y\leq d\) переменную \(y\) как неявную функцию \(x\), то связь между \(dy\) и \(dx\) можно установить, формально дифференцируя тождество \(F(x,y(x)) = 0\). Воспользовавшись инвариантностью формы дифференциала, получаем
$$
F_x(x,y)dx + F_y(x,y)dy = 0.\nonumber
$$
Дифференцируя последнее тождество еще раз, можем найти второй дифференциал \(d^2y\)
$$
F_
$$
Неявные функции, определяемые системой уравнений.
Рассмотрим систему \(m\) уравнений с \(n+m\) неизвестными
$$
\left\<\begin
$$
При формулировке общей теоремы о неявных функциях удобно пользоваться понятием декартова произведения множеств. Если \(A\) и \(B\) — произвольные множества, то их декартово произведение \(A\times B\) есть множество пар \((x,y)\), где \(x\in A\), \(y\in B\). Так, декартово произведение \([a,b]\times [c,d]\) есть множество пар вещественных чисел таких, что \(a\leq x\leq b,\) и \(c\leq y\leq d\), то есть прямоугольник в \(R^2\).
Клеточной окрестностью точки \(x^0 =(x_1^0,\ldots,x_n^0)\) будем называть следующее множество:
$$
K(x^0)=\
$$
где \(\varepsilon_i, \; i =\overline<1,n>\) — положительные числа, \(x = (x_1,…,x_n)\).
Легко видеть, что в том случае, когда \(K_1(x^0)\subset R^n\) и \(K_2(y^0)\subset R^m\) — клеточные окрестности, их декартово произведение \(K_1(x^0)\times K_2(y^0)\) есть клеточная окрестность точки \((x^0,y^0)=(x_1^0,…,x_n^0,y_1^0,…,y_m^0\) в пространстве \(R^
Для дальнейшего удобно преобразовать переменные, полагая \(x=(x_1,…,x_n), \; y=(y_1,…,y_m)\), где \(y_1=x_
Тогда систему уравнений \eqref
$$
F_i(x,y) = 0, \; i=\overline<1,m>.\label
$$
Функции \(F_i(x,y) = 0\) будем считать определенными в некоторой клеточной окрестности точки \((x^0,y^0)\).
Пусть \(K(x^0)\subset R^n\) и \(Q(y_0)\subset R^m\) есть клеточные окрестности. Будем говорить, что система уравнений \(F_i(x,y)=0, \; i=\overline<1,m>\), определяет в \(K(x^0)\times Q(y_0)\) переменные \(y_1,…,y_m\) как неявные функции переменных \(x_1,…,x_n\), если для любого \(x\in K(x^0)\) найдется единственный \(y\in Q(y^0)\) такой, что \(F_i(x,y) = 0, \; i=\overline<1,m>\).
Пусть выполнены следующие условия:
Тогда найдутся клеточные окрестности \(K(x^0) \subset R^n\) и \(Q(y^0) \subset R^m\) такие, что в \(K(x^0)\times Q(y^0)\) система уравнений \eqref
\(\circ\) Воспользуемся методом индукции по числу уравнений \(m\). При \(m=1\) доказательство теоремы 2 не отличается от доказательства теоремы 1 (в дальнейшем будем ссылаться на этот частный случай теоремы 2 как на теорему 1).
Предположим, что утверждение теоремы верно в том случае, когда система \eqref
Так как определитель \eqref
$$
<\begin
$$
(Здесь и в дальнейшем символ \(0\) означает, что значение соответствующей функции берется для аргументов с верхним индексом \(0\)).
Тогда в силу индукции найдутся такие клеточные окрестности
$$
\begin
Существует несколько способов доказательства теоремы о неявных функциях. Предложенный способ является, по-видимому, наиболее простым, но обладает двумя недостатками: не дает алгоритма для вычисления неявной функции и не обобщается на бесконечномерный случай.
Локальная обратимость регулярного отображения.
Пусть на множестве \(E\subset R^n\) заданы \(n\) функций
$$
f_1(x),…,f_n(x).\nonumber
$$
Они задают отображение \(f: \; E\rightarrow R^n\), которое каждой точке \(x\in E\) ставит в соответствие точку \(y=f(x)\), где
$$
y_1=f_1(x),\quad,…,\quad y_n=f_n(x).\nonumber
$$
Точка \(y=f(x)\) называется образом точки \(x\) при отображении \(f\). Точка \(x\) называется прообразом точки \(y\).
Если \(\Omega\subset E\), то множество
$$
f(\Omega)=\
$$
называется образом множества \(\Omega\) при отображении \(f\). Если \(\omega\subset f(E)\), то множество
$$
f^<-1>(\omega)=\
$$
называется прообразом множества \(\omega\).
Пусть \(G \subset R^n\) есть открытое множество. Отображение \(f: \; G\rightarrow R^n\) называется непрерывным в точке \(x^0\), если \(\forall \varepsilon > 0 \; \exists\delta > 0\) такое, что \(\forall x\) таких, что \(\rho(x,x^0) Лемма 1.
Если \(G\) есть открытое множество, а \(f: \; G\rightarrow R^n\) — непрерывное отображение, то прообраз каждого открытого множества \(\omega\in f(G)\) есть открытое множество.
\(\circ\) Пусть \(\Omega= f^<-1>(\omega)\). Возьмем любую точку \(x^0\in\Omega\). Тогда \(f(x^0)=y^0\in \omega\). Так как множество \(\omega\) открыто, то найдется окрестность \(S_<\varepsilon>(y^0)\in \omega\). В силу непрерывности отображения \(f\) в точке \(x^0\) найдется шаровая окрестность \(S_<\delta>(x^0)\), для которой выполнено условие \eqref
Следовательно,
$$
S_<\delta>(x^0)\subset f^<-1>(\omega)\subset\Omega,\nonumber
$$
и \(\Omega\) — открытое множество. \(\bullet\)
Как обычно, под окрестностью \(A(x^0)\) точки \(x^0\) будем понимать любое множество \(A\), для которого точка \(x^0\) внутренняя.
Пусть \(G \subset R^n\) — открытое множество. Отображение \(f: \; G\rightarrow R^n\) будем называть непрерывно дифференцируемым, если функции \(f_1(x),…,f_n(x)\), задающие это отображение, непрерывно дифференцируемы в \(G\). Непрерывно дифференцируемое отображение \(f: \; G\rightarrow R^n\) будем называть регулярным, если в области \(G\) якобиан отображения \(j_f(x)\neq 0\). Якобианом отображения \(j_f(x)\) называется следующий функциональный определитель:
$$
j_f(x)=\begin
$$
Пусть \(G\) — открытое множество в \(R^n\), а отображение \(f: \; G\rightarrow R^n\) регулярно. Тогда в каждой точке \(x^0\in G\) оно локально регулярно обратимо, то есть \(\forall x^0\in G\) найдутся такие окрестности \(A(x^0) \subset G\) и \(B(y^0)\subset f(G)\), где \(y^0= f(x^0)\), что отображение \(f: \; A(x^0)\rightarrow B(y^0)\) будет взаимно однозначным, причем обратное отображение \(f^<-1>: \; B(y^0)\rightarrow A(x^0)\) регулярно.
\(\circ\) Рассмотрим в \(G\times R^n\) систему уравнений
$$
F_i(x,y)\equiv y_i-f_i(x)=0,\quad i=\overline<1,n>.\label
$$
Пусть \(x^0\) — произвольная точка множества G и \(y^0=f(x^0)\). Тогда функции \(F_i(x,y)\) непрерывно дифференцируемы в \(G\times R^n\) и \(y_i^0= f_i(x^0), \; i=\overline<1,n>\). Так как отображение \(f\) регулярно, то Если \(f: \; G\rightarrow R^n\) есть регулярное отображение, то образ любого открытого множества \(\Omega\subset G\) есть открытое множество. \(\circ\) Пусть \(\omega=f(\Omega)\). Возьмем произвольную точку \(y^0\in\omega\) и пусть \(x^0\) есть какой-то ее прообраз. Тогда, вследствие теоремы 3, найдутся такие окрестности \(A(x^0) \subset \Omega\) и \(B(y^0) \subset \omega\); что отображение \(f: \; A(x^0)\rightarrow B(y^0)\) регулярно обратимо. Поэтому каждая точка \(y^0\in\omega\) принадлежит \(\omega\) вместе с некоторой окрестностью \(B(y^0)\). Множество \(\omega=f(\Omega)\) открыто. \(\bullet\) Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах. Теорема о неявной функции Мельник П.И ФМиКН, 5 курс Теорема о неявной функции Целеполагание Задача Параметр Выразить одну переменную через другую: Вхождение в тему Математическая разминка 2)Вычислить производную Теорема о неявной функции Организация учащихся Холодные числа, внешне сухие формулы математики полны внутренней красоты и жара сконцентрированной в них мысли. А.Д. Александров Теорема о неявной функции Теорема о неявной функции Определим функцию у = f(x) следующим образом: пусть каждому значению переменной х из некоторого множества поставлено в соответствие некоторое число у, такое что F(x; y) = 0. Такой способ задания называется неявным способом задания функции у = f(x), а сама эта функция – неявной функцией. Простейшая теорема о неявной функции состоит в следующем: Если функция F: R×R→R непрерывна в некоторой окрестности точки (x0,y0) F(x0,y0)=0 и при фиксированном x, функция F(x,y) строго монотонна по y в данной окрестности, тогда найдётся такой двумерный промежуток I=Ix×Iy , являющийся окрестностью точки (x0,y0 )и такая непрерывная функцияf: Ix→Iy , что для любой точки (x,y)∈I,F(x,y)=0 ↔y=f(x). Теорема о неявной функции Освоение новых знаний Пусть f(a,x)=ax2+(a+1)x+1, тогда f(a,x) – непрерывна как многочлен. Чтобы функция была монотонна достаточно, чтобы ее производная по x не равнялась нулю. Пример 1. Решить уравнение ax2+(a+1)x+1=0 Практикум ax2+(a+1)x+1=0 D=a2+2a+1-4a=a2-2a+1=(a-1)2 Ответ: x1=-1,x2=-1/a Теорема о неявной функции f ‘(a,x)=2ax+a+1, то есть в окрестности точки (0;0) функция f(a,x) – непрерывна и монотонна, тогда по теореме о неявной функции, в окрестности взятой точки найдется такая непрерывная функция f(a,x)=0 ↔ x=f(a). Т.е. в окрестности точки(0;0) исходное уравнение имеет корни: x1=-1,x2=-1/a. Т.к функция f(a,x) непрерывна на всей вещественной оси, то решения x1=-1,x2=-1/a будут решениями уравнения в любой точке. Практикум Пример2. Решить уравнение 22x-(2a+1) 2x+a2+a=0. Решение. Пусть f(a,x)=22x-(2a+1)2x+a2+a тогда f(a,x) – непрерывна как многочлен. Чтобы функция была монотонна достаточно, чтобы ее производная по не равнялась нулю. то есть в окрестности точки (0,0) функция f(a,x) – непрерывна и монотонна, тогда по теореме о неявной функции, в окрестности взятой точки найдется такая непрерывная функция f(a,x)=0 ↔ x=f(a). 22x-(2a+1) 2x+a2+a=0, Пусть 2x=t, t>0, тогда Теорема о неявной функции Практикум Пример2. Решить уравнение 22x-(2a+1) 2x+a2+a=0. Решение. Ответ: Теорема о неявной функции , . Задание для самостоятельного решения Решение. Пусть f(a,x)=a sinx-1, тогда f(a,x) – непрерывна как многочлен. Чтобы функция была монотонна достаточно, чтобы ее производная по x не равнялась нулю. f ‘(a,x)=a cosx; x≠π/2+πn, n∈Z, a∈R, то есть в окрестности точки (0,1) функция f(a,x) – непрерывна и монотонна, тогда по теореме о неявной функции, в окрестности взятой точки найдется такая непрерывная функция f(a,x)=0 ↔ x=f(a). Ответ: Проверка полученных результатов Решить уравнение a sin x=1 Теорема о неявной функции Домашнее задание Найти хотя бы одно решение Подведение игогов, рефлексия Мы с наслаждением познаём математику… Она восхищает нас, как цветок лотоса. Аристотель Получили ли вы наслаждение на уроке? Теорема о неявной функции (x0,y0)уравнение (1) определяет y как уникальную функцию x: _y=/(x); b) для x=x y эта функция принимает значение y:/(x0)=_u0;C) интервал А) пусть Ru'(x0, z>0)0. Производная от 1) R>эта производная положительна P’u Ko, _uo и движемся вдоль e R t и l I. 7), t-e-f и K s и R u E m x-x0; рассматриваемая функция P (x, y) сводится от одной переменной y к функции P (x%, y). Благодаря 2), что из y=y B изменяется на 0. В то же время, как мы теперь установили, значение y _u0 больше нуля, отношение o z p A C t A e t вместе с y, в частности, Ko, y (-8′) имеет другое знаковое значение в предыдущей точке, а значение P (Vo)=P (x0, l+8′)>0. Теперь изменим прямую, проходящую через эти точки, на g O R и z o n t a l n s m и исправим y-y y-8’or=_u0-|-8′. P (x, y-8′) и P (x, _uo+8′), который имеет x=x^: первый-3151§I. неявная функция 183 Отрицательные значения, а вторые-положительные. Однако, поскольку условие 1) эти функции непрерывны), существует окрестность (x0—B, x0-4-y) точки x o (O 0. Другими словами, в нижнем и верхнем основаниях D1D2 и XB%, учитывая, что вдоль отрезков длины 28, точки исходного прямоугольника имеют центры AO и B§. Рассмотрим вертикальный отрезок, соединяющий точку A (x, UY-In’) и s/0+^, фиксируя значение x=x(x0—b,x0) со значением x=x (x,UY-In’) и S / неявную функцию y=p (x), которая определяется формулой (1) по y и удовлетворяет ей таким же образом. Увеличенное значение X — (- D x соответствует 4-4U=/(x и уравнение, удовлетворяющее ему (1): P(x&x, y+A_u)=0. Очевидно, что приращение AT7 (x, y)=P (X Ah, y4-D_u)-p (x, y)=0. Здесь мы преобразуем это уравнение, используя формулу конечного приращения[n°102]: 0=P(x4-x&x,y Du) — P(x,_u)==[G(x4 Ah, z / +Du) — P (x, z/Du)]4- А-[Р^У+^ — Р^У)>= =Р ‘х(Х4 — ^х, У4″ Ду• * к Х4-ру(х, У4-61a_u)•A_u(0 0 имеет a_u->0, то есть функция y-R(x)непрерывна. У нас есть Du, / / M x+e D x, y+Du) / DX ru (x, Y+#Y) , но непрерывная функция b& / Px ‘ / ограничена сверху конечным числом Людмила Фирмаль 7I[n°137]] 1^-1^м , И в то же время, П О Л О В и т е л ь я непрерывная функция R>, имеющая наименьшее значение/n[n°137], также положительная, ограничена ею снизу: Ру т0. Теперь это легко получить баллы Я делаю свой M|DH I t Или / Г г|^1М Оттуда следует необходимое предложение.316]§1. Неявная функция 185 d) Если вы вернетесь к эквиваленту (3), скажем, x равно 0. Так как мы уже знаем, что одновременно и p’u->0, то рассмотрим непрерывность функций P’X и P’U и тот факт, что P’U0 находится справа от полученного нами предела. Р’х у) Р У(,У)’ Таким будет предел левой части уравнения (3), поэтому существует производная y по x: L (x)=Y^=NT_ _ R’X ( * , Y) Р у (, у)’ (4) Если вы назначаете/(x) вместо Y, вы получаете /'() = ^(Х,/(Х ) ) P y (, /()) ‘так как числитель и знаменатель имеют непрерывные функции и знаменатель не исчезает, то ясно, что/'(x)также является непрерывной функцией. Теорема прекрасно доказана. Таким образом, по характеристикам функции/(x, y), заданным непосредственно нам, мы можем определить характеристики функции _y=/(x), которая не имеет непосредственной работы! Мы уже упоминали в пункте 314 геометрическую интерпретацию вопросов, которые мы здесь изучили. Если кривая задана «неявным» уравнением (1) и ее потоком P\, 0, то в окрестности этой точки кривая может быть представлена»явным»уравнением вида следующего, конечно, x и y могут поменяться ролями: если в какой-то точке в окрестности P’x0 кривая может быть представлена тем же»явным»уравнением только в[210] (как P’x=0, так и p’u=0), то наша теорема не находит применения. 316 Неа Образовательный сайт для студентов и школьников Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника. © Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института http://infourok.ru/prezentaciya-po-matematike-teorema-o-neyavnoy-funkcii-v-reshenii-zadach-s-parametrami-1127171.html http://lfirmal.com/sushchestvovanie-i-svoystva-neyavnoy-funkcii/
$$
<\begin
$$
Для системы уравнений \eqref
$$
\begin
$$
что в \(K(x^0)\times Q(y^0)\) система уравнений \eqref
$$
\begin
$$
Пусть \(B(y^0)\) есть внутренность \(Q(y^0)\):
$$
B(y^0) = \left\Презентация по математике «Теорема о неявной функции в решении задач с параметрами»
Описание презентации по отдельным слайдам:
Существование и свойства неявной функции

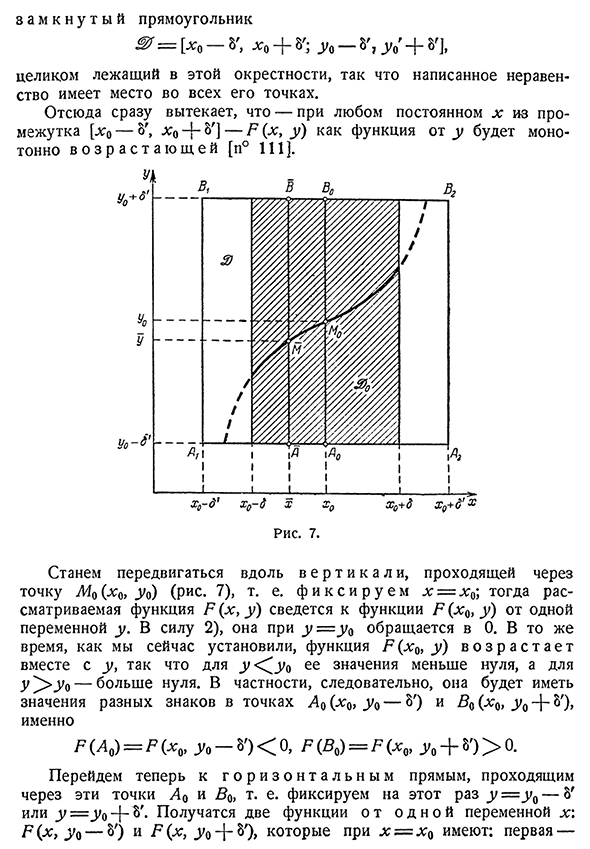



Существование и свойства неявной функции
























































