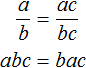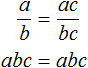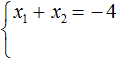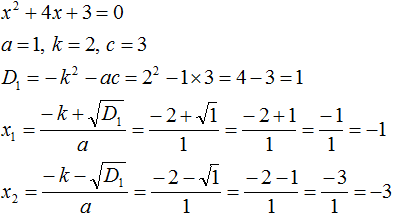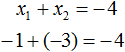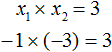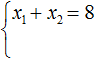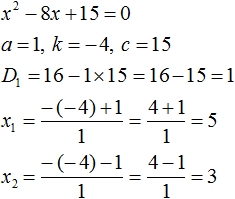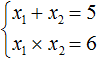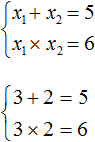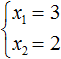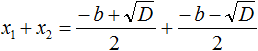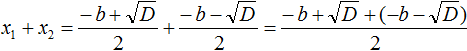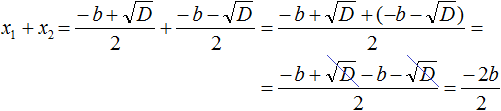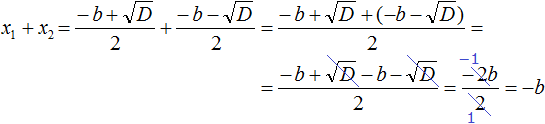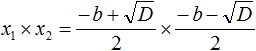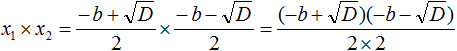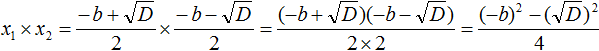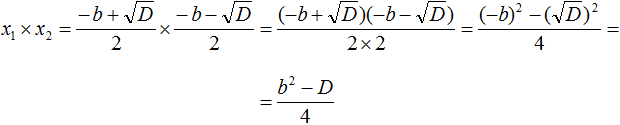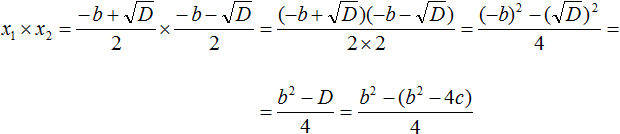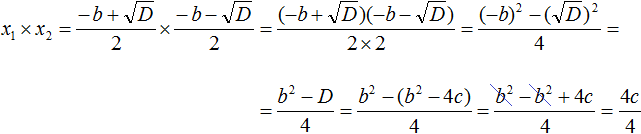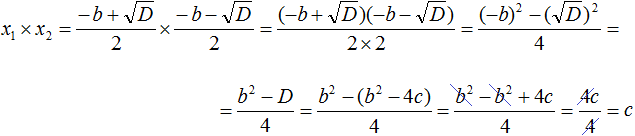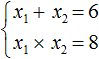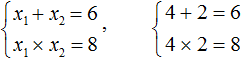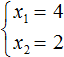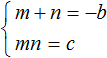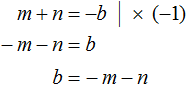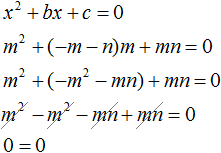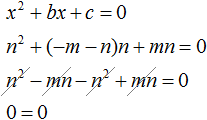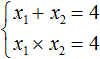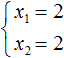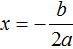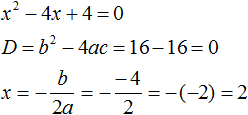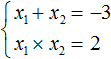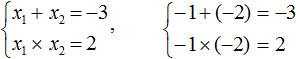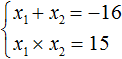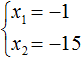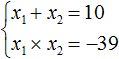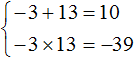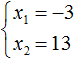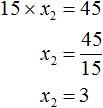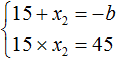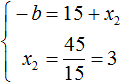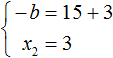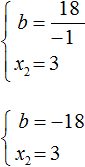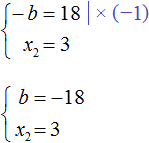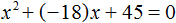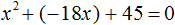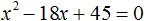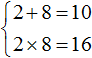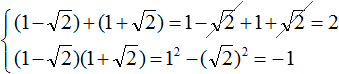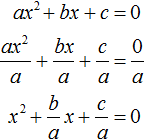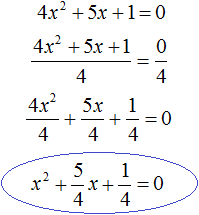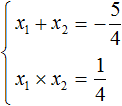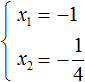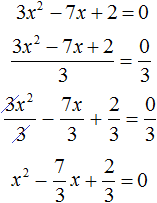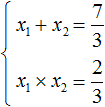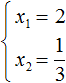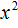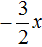Уравнения высших степеней
Вы будете перенаправлены на Автор24
Уравнения высших степеней — это уравнения, в которых старшая степень при переменной больше либо равна трём. На данный момент не существует какой-либо единой схемы для решения уравнений высших степеней.
Наиболее известными схемами для решения являются:
- Формула Кардано, он подходит только для уравнений 3-ьей степени;
- Метод Феррари для уравнений 4-ой степени;
- Теорема Виета для степени больше двух;
- Теорема Безу;
- Схема Горнера.
Ниже рассмотрены основные методы решения уравнений высших степеней с целыми и рациональными коэффициентами, справедливые для разных степеней.
Теорема Виета
Рассмотрим уравнение вида $ax^3+bx^2+cx+d=0$.
Данное уравнение обладает тремя корнями и для того чтобы его решить в общем виде, необходимо решить следующую систему:
Иначе эти системы уравнений также называют формулами Виета.
Решите уравнение: $x^3+x^2-4x-4=0$.
Решение:
Составим систему уравнений:
$\begin
Решив её, получим следующие корни:
Теорема Безу
Суть этой теоремы в том, что если уравнение вида $a_0x^n + a_1x^
Алгоритм при решении уравнения с использованием теоремы Безу следующий:
- Найти и выписать все делители свободного члена.
- Проверять эти делители до тех пор, пока не будет найден хотя бы один, являющийся корнем уравнения.
- Разделить всё уравнение на $(x-α)$ и записать само уравнение как произведение $(x-α)$ и результата выполненного деления.
- Решить полученное после разложения уравнение.
Готовые работы на аналогичную тему
Решение:
Делители члена не при переменной: $±1;±2;±3;±6$
Подставим $1$ в корень уравнения и получим, что наше равенство выполняется:
Следовательно, $x_1=1$ — один из корней уравнения. Теперь необходимо выполнить деление многочлена столбиком:
Рисунок 1. Схема деления многочлена столбиком. Автор24 — интернет-биржа студенческих работ
После этого исходное уравнение можно записать разложив на множители:
Решаем полученное квадратное уравнение и получаем ещё 2 корня: $x_<2,3>=-3;-2$.
Схема Горнера
Схема Горнера состоит в том, чтобы также сначала найти какой-либо корень уравнения вида $a_0x^n + a_1x^
После этого составляется специальная таблица с результатами деления на $(x-α)$, в которой каждый член зависим от предыдущего. Коэффициенты из данной таблицы используются как коэффициенты в полученном от деления частного многочлене, они вычисляются по формулам:
$b_0=a_0; b_1=αb_0+a_1; b_2=αb_1+a_2. b_
Рисунок 2. Таблица для вычисления коэффициентов по схеме Горнера. Автор24 — интернет-биржа студенческих работ
Решение:
Делители свободного члена — $±1;±2;±3;±6$
Запишем таблицу со коэффициентами:
Рисунок 3. Схема Горнера: пример. Автор24 — интернет-биржа студенческих работ
Отсюда получаем, что многочлен, полученный от деления на $(x-α)$ при $α=1$, равен $x^2+5x+6$.Получается, что исходное уравнение принимает вид:
Корни же второго многочлена будут $x_<2,3>=-2;-3$.
Метод одновременного подбора по коэффициенту при старшей степени и при свободном члене
Данный метод основан на следующем условии:
Несократимая дробь $\frac
$ будет корнем уравнения, если числитель этой дроби является делителем свободного члена, а знаменатель — делителем коэффициента, стоящего при члене со старшей степенью.
Алгоритм этого метода:
- Поиск делителей свободного члена.
- Поиск делителей коэффициента, стоящего при члене со старшей степенью.
- Составление дробей и подбор решения.
Решение:
Делители свободного члена: $±1; ±2; ±3; ±6$.
Делители коэффициента при старшем члене: $1; 2$.
Следовательно, как корни нужно проверить следующие значения: $1;-1;2;-2;3;-3;6;-6;\frac<1><2>; -\frac<1><2>; \frac<3><2>; -\frac<3><2>$.
Подставив эти числа в уравнения, получим, что корнями уравнения являются $x_1=1;x_2= \frac<1><2>$.
Это значит, что многочлен можно разделить на $2(x-1)(x-\frac<1><2>)=2x^2-3x+1$. При выполнении деления получаем частное $x^2+10x+6$.
Приравниваем этот многочлен к нулю и находим его корни через дискриминант, они равны $x_<3,4>=-5±\sqrt<19>$.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 14 03 2021
Теорема Виета
Что называют теоремой?
Если человек обнаружил в математике какую-нибудь закономерность, позволяющую быстро решить ту или иную задачу, то ему не следует говорить о том, что он сделал открытие. Потому что может случиться так, что эта закономерность работает только для определённых случаев, а для других не работает или вовсе решает задачу неправильно.
Чтобы поделиться своим открытием с другими людьми, найденную закономерность следует сформулировать в виде утверждения, а затем доказать это утверждение, приводя неоспоримые факты.
Сформулированное утверждение называют теоремой. А доказательство теоремы состоит из фактов, логических рассуждений и вычислений, которые не оспариваются.
Например, теоремой можно назвать следующее утверждение:
«Если числитель и знаменатель обыкновенной дроби умнóжить на какое-нибудь число, то значение данной дроби не измéнится».
А затем привести такое доказательство:
Пусть, имеется дробь 
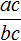

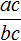
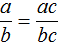
Для доказательства этого равенства воспользуемся основным свойством пропорции:
От перестановки мест сомножителей произведение не меняется. Поэтому в получившемся равенстве можно упорядочить правую часть по алфавиту:
Поскольку равенство 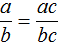

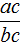
Теорема Виета
Французский математик Франсуа Виет выявил интересную взаимосвязь между коэффициентами приведённого квадратного уравнения и корнями этого же уравнения. Эта взаимосвязь представлена в виде теоремы и формулируется так:
Сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком, а произведение корней равно свободному члену.
То есть, если имеется приведённое квадратное уравнение x 2 + bx + c = 0 , а его корнями являются числа x1 и x2 , то справедливы следующие два равенства:
Знак системы (фигурная скобка) говорит о том, что значения x1 и x2 удовлетворяют обоим равенствам.
Покажем теорему Виета на примере приведённого квадратного уравнения x 2 + 4x + 3 = 0 .
Мы пока не знаем какие корни имеет уравнение x 2 + 4x + 3 = 0 . Но по теореме Виета можно записать, что сумма этих корней равна второму коэффициенту 4 , взятому с противоположным знáком. Если коэффициент 4 взять с противоположным знáком, то получим −4 . Тогда:
А произведение корней по теореме Виета будет равно свободному члену. В уравнении x 2 + 4x + 3 = 0 свободным членом является 3 . Тогда:
Теперь проверим действительно ли сумма корней равна −4 , и равно ли произведение 3 . Для этого найдём корни уравнения x 2 + 4x + 3 = 0 . А для удобства воспользуемся формулами для чётного второго коэффициента:
Корнями уравнения являются числа −1 и −3 . По теореме Виета их сумма должна была равняться второму коэффициенту уравнения x 2 + 4x + 3 = 0 , взятому с противоположным знаком. Действительно, так оно и есть. Вторым коэффициентов в уравнении x 2 + 4x + 3 = 0 является 4 . Если взять его с противоположным знаком и приравнять сумму корней x1 + x2 к этому коэффициенту, то получается верное равенство:
А произведение корней −1 и −3 по теореме Виета должно было равняться свободному члену уравнения x 2 + 4x + 3 = 0 , то есть числу 3 . Видим, что это условие тоже выполняется:
Значит выражение 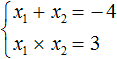
Рассмотрим квадратное уравнение x 2 − 8x + 15 = 0 . По теореме Виета сумма корней этого уравнения равна второму коэффициенту, взятому с противоположным знаком. Второй коэффициент равен −8 . Если взять его с противоположным знаком, то получим 8 . Тогда:
А произведение корней равно свободному члену. В уравнении x 2 − 8x + 15 = 0 свободным членом является 15 . Тогда:
Теперь проверим действительно ли сумма корней равна 8 , и равно ли произведение 15 . Для этого найдём корни данного уравнения. А для удобства воспользуемся формулами для чётного второго коэффициента. В этот раз пропустим нéкоторые подробные записи:
Видим, что корнями уравнения x 2 − 8x + 15 = 0 являются числа 5 и 3 . Их сумма равна 8 . То есть сумма корней равна второму коэффициенту уравнения x 2 − 8x + 15 = 0 , взятому с противоположным знаком.
А произведение чисел 5 и 3 равно 15 . То есть равно свободному члену уравнения x 2 − 8x + 15 = 0 .
Значит выражение 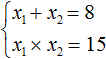
Замечание. Чтобы теорема Виета выполнялась, квадратное уравнение обязательно должно быть приведённым и иметь корни.
Например, рассмотрим квадратное уравнение x 2 − 2x + 4 = 0 . Напишем сумму и произведение корней этого уравнения:
Но уравнение x 2 − 2x + 4 = 0 не имеет корней, сумма которых равна 2, а произведение которых равно 4 . Убедиться в этом можно, вычислив дискриминант:
А значит записывать выражение 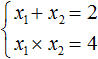
Теорема Виета полезна тем, что позволяет до начала решения узнать знаки корней уравнения.
Например, запишем для уравнения x 2 − 5x + 6 = 0 сумму и произведение его корней. Сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
Посмотрев на эти два равенства можно сразу понять, что оба корня должны быть положительными. Потому что произведение x1 × x2 = 6 будет выполняться только в двух случаях: если значения x1 и x2 положительны либо они оба отрицательны. Если эти значения будут отрицательными, то не будет выполняться равенство x1 + x2 = 5 , поскольку его правая часть равна положительному числу. А значения x1 и x2 должны удовлетворять как равенству x1 + x2 = 5 , так и равенству x1 × x2 = 6.
Ещё одна польза от теоремы Виета в том, что корни можно найти методом подбора. В данном примере корни должны быть такими, чтобы они удовлетворяли как равенству x1 + x2 = 5 так и равенству x1 × x2 = 6 . Очевидно, что таковыми являются корни 3 и 2
Доказательство теоремы Виета
Пусть дано приведённое квадратное уравнение x 2 + bx + c = 0 . Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
Вспомним формулы корней квадратного уравнения:
Найдём сумму корней x1 и x2 . Для этого подставим в выражение x1 + x2 вместо x1 и x2 соответствующие выражения из правой части формул корней квадратного уравнения. Не забываем, что в приведённом квадратном уравнении x 2 + bx + c = 0 старший коэффициент a равен единице. Тогда в процессе подстановки знаменатель станет равен просто 2
Запишем правую часть в виде дроби с одним знаменателем:
Раскроем скобки в числителе и приведём подобные члены:
Сократим дробь 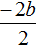
Теперь аналогично докажем, что произведение x1 × x2 равно свободному члену c .
Подставим вместо x1 и x2 соответствующие выражения из формул корней квадратного уравнения. Не забываем, что коэффициент a всё ещё равен единице:
Чтобы перемнóжить дроби, нужно перемнóжить их числители и знаменатели:
В числителе теперь содержится произведение суммы двух выражений и разности этих же выражений. Воспользуемся тождеством (a + b)(a − b) = a 2 − b 2 . Тогда в числителе полýчится 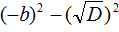
Теперь в числителе выражение (−b) 2 станет равно b 2 , а выражение 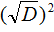
Но D равно b 2 − 4ac . Подстáвим это выражение вместо D , не забывая что a = 1 . То есть вместо b 2 − 4ac надо подставить b 2 − 4c
В получившемся выражении раскроем скобки в числителе и приведём подобные члены:
Сократим получившуюся дробь на 4
Таким образом, сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком ( x1 + x2 = −b ), а произведение корней равно свободному члену ( x1 × x2 = c ). Теорема доказана.
Теорема, обратная теореме Виета
Когда записана сумма и произведение корней приведённого квадратного уравнения, обычно начинается подбор подходящих корней к этому уравнению. В этот момент в работу включается так называемая теорема, обратная теореме Виета. Она формулируется так:
Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел x1 и x2 равно свободному члену уравнения x 2 + bx + c = 0, то числа x1 и x2 являются корнями уравнения x 2 + bx + c = 0.
Обратные теоремы бывают поставлены так, что их утверждением является заключение первой теоремы.
Так, доказывая теорему Виета мы пришли к заключению, что сумма x1 и x2 равна −b , а произведение x1 и x2 равно c . В обратной же теореме это заключение служит утверждением.
Ранее мы решили уравнение x 2 − 5x + 6 = 0 и написали для него такую сумму и произведение корней:
А затем подобрали корни 3 и 2 . По сути мы применили теорему, обратную теореме Виета. Числа 3 и 2 таковы, что их сумма равна второму коэффициенту уравнения x 2 − 5x + 6 = 0 , взятому с противоположным знаком (числу 5 ), а произведение чисел 3 и 2 равно свободному члену (числу 6 ). Значит числа 3 и 2 являются корнями уравнения x 2 − 5x + 6 = 0 .
Пример 2. Решить квадратное уравнение x 2 − 6x + 8 = 0 по теореме, обратной теореме Виета.
В данном уравнении a = 1 . Значит квадратное уравнение является приведённым. Его можно решить по теореме, обратной теореме Виета.
Сначала запишем сумму и произведение корней уравнения. Сумма корней будет равна 6 , поскольку второй коэффициент исходного уравнения равен −6 . А произведение корней будет равно 8
Теперь имея эти два равенства можно подобрать подходящие корни. Они должны удовлетворять как равенству x1 + x2 = 6 , так и равенству x1 × x2 = 8
Подбор корней удобнее выполнять с помощью их произведения. Используя равенство x1 × x2 = 8 нужно найти такие x1 и x2 , произведение которых равно 8.
Число 8 можно получить если перемножить числа 4 и 2 либо 1 и 8.
4 × 2 = 8
1 × 8 = 8
Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли не только равенству x1 × x2 = 8 , но и равенству x1 + x2 = 6 .
Сразу делаем вывод, что значения 1 и 8 не годятся, поскольку они хоть и удовлетворяют равенству x1 × x2 = 8 , но не удовлетворяют равенству x1 + x2 = 6 .
Зато значения 4 и 2 подходят как равенству x1 × x2 = 8 , так и равенству x1 + x2 = 6 , поскольку эти значения удовлетворяют обоим равенствам:
Значит корнями уравнения x 2 − 6x + 8 = 0 являются числа 4 и 2 .
Обратная теорема, как и любая теорема нуждается в доказательстве. Докажем теорему, обратную теореме Виета. Для удобства корни x1 и x2 обозначим как m и n . Тогда утверждение теоремы, обратной теореме Виета примет следующий вид:
Если числа m и n таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел m и n равно свободному члену уравнения x 2 + bx + c = 0, то числа m и n являются корнями уравнения x 2 + bx + c = 0
Для начала запишем, что сумма m и n равна −b , а произведение mn равно c
Чтобы доказать, что числа m и n являются корнями уравнения x 2 + bx + c = 0 , нужно поочередно подстáвить буквы m и n в это уравнение вместо x , затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями уравнения x 2 + bx + c = 0 .
Помимо букв m и n нам нужно знать чему равен параметр b . Выразим его из равенства m + n = −b . Легче всего это сделать, умножив обе части этого равенства на −1
Теперь всё готово для подстановок. Подстáвим m в уравнение x 2 + bx + c = 0 вместо x , а выражение −m − n подставим вместо b
Видим, что при x = m получается верное равенство. Значит число m является корнем уравнения x 2 + bx + c = 0 .
Аналогично докажем, что число n является корнем уравнения x 2 + bx + c = 0 . Подставим вместо x букву n , а вместо c подставим mn , поскольку c = mn .
Видим, что при x = n тоже получается верное равенство. Значит число n является корнем уравнения.
Следовательно, числа m и n являются корнями уравнения x 2 + bx + c = 0 .
Примеры решения уравнений по теореме, обратной теореме Виета
Пример 1. Решить квадратное уравнение x 2 − 4x + 4 = 0 по теореме, обратной теореме Виета.
Запишем сумму корней x1 и x2 и приравняем её к второму коэффициенту, взятому с противоположным знаком. Также запишем произведение корней x1 и x2 и приравняем его к свободному члену :
В данном примере очевидно, что корнями являются числа 2 и 2 . Потому что их сумма равна 4 и произведение равно 4
Значение x1 совпадает с x2 . Это тот случай, когда квадратное уравнение имеет только один корень. Если мы попробуем решить данное уравнение с помощью формул корней квадратного уравнения, то обнаружим что дискриминант равен нулю, и корень вычисляется по формуле
Данный пример показывает, что теорема обратная теореме Виета, работает и для уравнений, имеющих только один корень. Признаком того, что квадратное уравнение имеет только один корень является то, что значения x1 и x2 совпадают.
Пример 2. Решить уравнение x 2 + 3x + 2 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Теперь подберём значения x1 и x2 . Здесь начинается самое интересное. Произведение корней равно 2 . Число 2 можно получить перемножив 1 и 2 . Но сумма корней x1 + x2 равна отрицательному числу −3 . Значит значения 1 и 2 не подходят.
Сумма бывает отрицательной если оба слагаемых отрицательны либо отрицательным является одно слагаемое, модуль которого больше.
Если подберём корни с разными знаками, то не будет выполняться равенство x1 × x2 = 2 .
Если подберем положительные корни, то будет выполняться равенство x1 × x2 = 2 , но не будет выполняться равенство x1 + x2 = −3 .
Очевидно, что корнями являются два отрицательных числа. Произведение отрицательных чисел есть положительное число. А сумма отрицательных чисел есть отрицательное число.
Тогда равенствам будут удовлетворять числа −1 и −2 .
Итак, корнями являются числа −1 и −2
Пример 3. Решить уравнение x 2 + 16x + 15 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Как и в прошлом примере сумма корней равна отрицательному числу, а произведение корней — положительному числу.
Произведение бывает положительным если оба сомножителя положительны либо оба сомножителя отрицательны. Первый вариант отпадает сразу, поскольку сумма корней равна отрицательному числу. Тогда получается, что оба корня будут отрицательными. Попробуем подобрать их.
Число 15 можно получить, если перемножить числа −1 и −15 или (−3) и (−5) . В данном случае подходит первый вариант, поскольку сумма чисел −1 и −15 равна −16 , а их произведение равно 15 . Значит корнями уравнения x 2 + 16x + 15 = 0 являются числа −1 и −15
Пример 4. Решить уравнение x 2 − 10x − 39 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Произведение корней равно отрицательному числу. Значит один из корней является отрицательным. Число −39 можно получить если перемножить числа −3 и 13 либо −13 и 3 . Из этих комбинаций больше годится комбинация −3 и 13 , поскольку при перемножении этих чисел получается −39 , а при сложении 10
Значит корнями уравнения x 2 − 10x − 39 = 0 являются числа −3 и 13
Пример 5. Первый корень уравнения x 2 + bx + 45 = 0 равен 15 . Найти второй корень этого уравнения, а также значение коэффициента b .
По теореме Виета произведение корней приведённого квадратного уравнения равно свободному члену. В данном случае это произведение равно 45
При этом один из корней уже известен — это корень 15 .
Тогда второй корень будет равен 3 , потому что число 45 получается, если 15 умножить на 3
Этот второй корень также можно было бы получить, выразив из равенства 15 × x2 = 45 переменную x2
Теперь определим значение коэффициента b . Для этого напишем сумму корней уравнения:
По теореме Виета сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней равна 18, а 18 это положительное число, то в самóм уравнении этот коэффициент будет отрицательным:
Обычно решение к такой задаче записывают так. Сначала записывают основную теорему Виета в виде суммы и произведения корней:
Затем в это выражение подставляют имеющиеся известные значения. В нашем случае известно, что первый корень равен 15 , а свободный член уравнения x 2 + bx + 45 = 0 равен 45
Из этой системы следует найти x2 и b . Выразим эти параметры:
Из этой системы мы видим, что x2 равно 3. Подставим его в первое равенство:
Теперь из первого равенства мы видим, что −b равно 18
Но нас интересует b , а не −b . Следует помнить, что −b это −1b . Чтобы найти b нужно 18 разделить на −1 . Тогда b станет равно −18
Этот же результат можно получить если в выражении 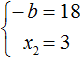
Теперь возвращаемся к исходному уравнению x 2 + bx + 45 = 0 и подставляем найденное значение b
Выполним умножение −18 на x . Получим −18x
Пример 6. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа 2 и 8 .
В этом задании корни уже известны. То есть x1 = 2 , x2 = 8 . По ним надо составить квадратное уравнение вида x 2 + bx + c = 0 .
Запишем сумму и произведение корней:
По теореме Виета сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней 2 и 8 равна 10 , то в самóм уравнении число 10 должно быть с противоположным знаком. Значит b = −10 .
Произведение корней по теореме Виета равно свободному члену. У нас это произведение равно 16 .
Значит b = −10 , c = 16 . Отсюда:
Пример 7. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа 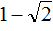
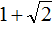
Запишем сумму и произведение корней:
Сумма корней равна 2. Тогда в уравнении второй коэффициент будет равен −2. А произведение корней равно −1. Значит свободный член будет равен −1. Тогда:
Когда квадратное уравнение неприведённое
Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым.
Если квадратное уравнение не является приведённым, но всё равно возникла необходимость применить теорему Виета, то обе части неприведённого квадратного уравнения следует разделить на коэффициент, который располагается перед x 2 .
Если к примеру в квадратном уравнении a x 2 + bx + c = 0 коэффициент a не равен единице, то данное уравнение является неприведённым. Чтобы сделать его приведённым, надо разделить обе его части на коэффициент, который располагается перед x 2 , то есть на a
Получилось уравнение 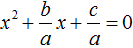


Например, решим квадратное уравнение 4x 2 + 5x + 1 = 0 . Это уравнение не является приведённым. Приведённым оно станет, если разделить обе его части на коэффициент, который располагается перед x 2 , то есть на 4
Получили приведённое квадратное уравнение. В нём второй коэффициент равен 

Отсюда методом подбора находим корни −1 и
Возможно этот метод вы редко будете использовать при решении квадратных уравнений. Но знать о нём не помешает.
Пример 2. Решить квадратное уравнение 3x 2 − 7x + 2 = 0
Данное уравнение не является приведённым, а значит его пока нельзя решить по теореме, обратной теореме Виета.
Сделаем данное уравнение приведенным. Разделим обе части на коэффициент, который располагается перед x 2
Получили уравнение 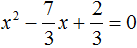
Отсюда методом подбора находим корни 2 и
Пример 3. Решить квадратное уравнение 2x 2 − 3x − 2 = 0
Это неприведённое квадратное уравнение. Чтобы сделать его приведённым, нужно разделить обе его части на 2 . Сделать это можно в уме. Если 2x 2 разделить на 2 , то полýчится x 2
Далее если −3x разделить на 2 , то полýчится 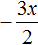
Далее если −2 разделить на 2 , то полýчится −1
Прирáвниваем получившееся выражение к нулю:
Теперь применяем теорему Виета. Сумма корней будет равна второму коэффициенту, взятому с противоположным знáком, а произведение корней свободному члену:
Отсюда методом подбора находим корни 2 и
Творческие проекты и работы учащихся
В ходе работы над исследовательским проектом по математике на тему «Теорема Виета в уравнениях N-степени» учащаяся 10 класса определила спектр задач, которые нужно уметь решать в данной теме, составила алгоритмы решения уравнений и связанных с ними задач с помощью т. Виета.
Подробнее о проекте:
В рамках выполнения проекта о теореме Виета представлено применение теоремы Виета в решении уравнений и задач, примеры задач с параметром, а также методы, применяемые при решении уравнений 3 и 4 степени. Была произведена разработка интерактивного тренажера «Теорема Виета в уравнениях 3 и 4 степени», анализ тренажеров и характеристика сетевого сервиса, с помощью которого будет создаваться продукт.
Оглавление
Введение
1. Основные теоретические сведения
2. Основные понятия
3. Методы, применяемые при решении уравнений 3 и 4 степени
4. Теорема Виета в решении уравнений n степени
Выводы по главе
5. Задачи, решаемые с использованием теоремы Виета
6. Применение теоремы Виета в решении уравнений и задач
7. Примеры решения уравнений и задач
8. Примеры решения задач с параметром
Выводы по главе
9. Разработка интерактивного тренажера «Теорема Виета в уравнениях 3 и 4 степени»
10. Анализ тренажеров и характеристика сетевого сервиса, с помощью которого будет создаваться продукт
11. Создание контента тренажера
12. Апробация продукта
Заключение
Список литературы
в заданиях ЕГЭ и олимпиадных задачах часто встречается необходимость решать уравнения n степени и задачи, связанные с ними.
нам часто приходится решать уравнения n степени и связанные с ними задачи, но некоторым способам их решения уделяется недостаточно внимания при изучении, из-за чего они не используются учениками.
изучить применение теоремы Виета для решения уравнений n степени.
данный проект может быть полезен ученикам старшей школы при решении уравнений степени выше 2.
интерактивный тренажёр. Критерии: понятность, удобный интерфейс, доступность, бесплатность.
Введение
Данный проект посвящен решению уравнений n степени с помощью теоремы Виета. Проект является актуальным, т.к. в заданиях ЕГЭ и олимпиадных задачах часто встречается необходимость решать уравнения n степени и задачи, связанные с ними. При выполнении различных заданий на уроках математики я столкнулась с проблемой, что нам часто приходится решать уравнения n степени и различные основанные на них задачи, но некоторым способам их решения уделяется недостаточно внимания при изучении, из-за чего они не используются учениками.
данного проекта являются уравнения. Предмет исследования: способы решения уравнений.
Также была поставлена цель: изучить применение теоремы Виета для решения уравнений n степени.
Для дополнительной практики в данной теме продуктом проекта был выбран интерактивный тренажер. Для удобного и продуктивного использования тренажера необходимо установить критерии оценки продукта: понятность предоставляемой информации, удобный интерфейс, доступность, бесплатность.
После была сформулирована гипотеза, что использование тренажера позволит ученикам самостоятельно научиться применять теорему Виета при решении уравнений n степени.
В процессе создания проекта были поставлены некоторые
- изучить литературу о применении теоремы Виета в решении уравнений n степени;
- определить спектр задач, которые нужно уметь решать в данной теме;
- составить алгоритмы решения уравнений и связанных с ними задач с помощью теоремы Виета;
- проанализировать тренажёры, предлагаемые в Интернете;
- выбрать платформу для создания интерактивного тренажера;
- составить тренажер по заданным критериям;
- апробировать тренажёр, сравнить с заданными критериями;
- отредактировать недочеты;
- провести предзащиту;
- защитить проект.
, используемые при работе над проектом: изучение и обобщение, анализ, сравнение, анкетирование.
в результате работы над проектом был создан уникальный интерактивный тренажер для практики в решении уравнений n степени с помощью теоремы Виета.
был разработан алгоритм решения уравнений 3 и 4 степени с применением теоремы Виета.
созданный тренажер может использоваться учениками для дополнительного изучения данной темы и подготовки к ЕГЭ, а также учителями.
данный проект может быть полезен ученикам старшей школы при решении уравнений степени выше 2.
- Основные теоретические сведения
В этой главе будут рассмотрены основные понятия и различные методы, которые используются при решении уравнений n степени.
- уравнение- математическое равенство, содержащее неизвестные величины;
- корень уравнения- значение переменной, при котором данное равенство обращается в верное;
- переменная- величина, которая может изменять своё (как правило, численное) значение;
- решить уравнение- найти все значения переменных, при которых выполняется равенство, или доказать, что их нет.
Приведем алгоритм деления многочлена на двучлен с помощью
- записать многочлен в стандартном виде;
- выразить из двучлена x (x=a);
- записать в первой строке таблицы коэффициенты многочлена в порядке убывания (an, an-1, …, a1, a0);
- заполнить таблицу по правилу.
Выполнить деление многочленов по схеме Горнера.
Ещё одним методом, применяемым при решении уравнений n степени является теорема Безу. Подобная теорема, по сути, была сформулирована ещё в 1687 году Исааком Ньютоном в первом томе его труда «Математические начала натуральной философии». Позднее, в 1779 году, эта теорема была опубликована французским математиком Этьеном Безу. Формулировка теоремы Безу: остаток от деления многочлена P(x) на двучлен x-a равен значению этого многочлена при x= a.
Разберем алгоритм нахождения остатка от деления многочлена на двучлен с помощью теоремы Безу:
- записать многочлен в стандартном виде;
- определить, чему равно a;
- посчитать значение многочлена P(a);
- получить остаток R=P(a) (если R=0, то многочлен P(x) делится на двучлен x-a, и a- корень многочлена).
В данной главе были разобраны некоторые методы решения уравнений n степени (схема Горнера, теорема Безу, метод решения возвратных уравнений), которые часто используются на практике, а также доказательства теоремы Виета для уравнений 3 и 4 степени. Рассмотренные методы достаточно просты в применении и всегда позволяют прийти к верному результату.
- Задачи, решаемые с использованием теоремы Виета
В данной главе будут рассмотрены примеры и способы решения различных задач, в основе которых лежат уравнения 3 и 4 степени, с использованием теоремы Виета.
Для начала необходимо отметить, что применение теоремы Виета для уравнений 3 и 4 степени разумно, если задано некоторое условие на корни многочлена.
Решая задачи на нахождение значений выражений, зависящих от корней многочлена, с применением теоремы Виета, стоит обратить внимание на то, что эти выражения не изменяются при перестановке корней, следовательно, они являются симметрическими многочленами, в которых переменными служат обозначения корней многочлена.
Таким образом, значение любого симметрического многочлена от n переменных, где вместо переменных подставлены все корни данного многочлена n-й степени, может быть выражено только через коэффициенты данного многочлена. Следовательно, в решении задач, связанных с корнями уравнений n степени, нужно стремиться представить данный многочлен через основные симметрические многочлены.
Рассмотрим основные шаги решения подобных задач:
- определить степень многочлена;
- записать теорему Виета для выражения необходимой степени;
- представить данный многочлен через основные симметрические многочлены;
- вычислить необходимые значения;
- записать ответ.
Отдельно выделим алгоритм решения системы уравнений, представляющих собой
- используя уравнения системы и формулы Виета составить уравнение (корни полученного уравнения будут решениями исходной системы);
- разложить многочлен на множители;
- найти корни уравнения;
- записать ответ.
Теорема Виета также применяется в решении уравнений, но необходимо отметить, что данный способ применим только к уравнениям, имеющим целые корни.
В качестве продукта проекта был выбран интерактивный тренажер, который позволит попрактиковаться в решении уравнений 3 и 4 степени с помощью теоремы Виета. Размещение тренажера на сетевой платформе позволит сделать данный продукт доступным для всех, кто хочет разобраться в этой теме.
При создании продукта были проанализированы следующие сетевые сервисы:
- LearningApps
- Quizizz
- Wordwall
- PurposeGames
- Wizer .me
Платформы были проанализированы по критериям:
- интуитивно понятный и удобный в использовании интерфейс сайта;
- возможность составления разнотипных заданий, для создания интересного и разнообразного контента;
- возможность бесплатного использования ресурсов сетевого сервиса при создании и дальнейшем использовании тренажера;
- доступность (возможность быстрого распространения (с помощью ссылок, QR-кодов и т.п.) и использования);
- наличие мобильной версии;
- возможность использования русского языка.
В данной таблице приведены результаты оценки сетевых сервисов по выбранным критериям:
| Критерии | |||
| Сетевой сервис | Интерфейс | Разнообразие шаблонов | Бесплатность |
| LearningApps | + | + | + |
| Quizizz | + | — | + |
| Wordwall | + | + | — |
| PurposeGames | + | + | + |
| Wizer .me | + | + | + |
| Критерии | |||
| Сетевой сервис | Доступность | Мобильная версия | Русский язык |
| LearningApps | + | — | + |
| Quizizz | + | + | — |
| Wordwall | + | + | + |
| PurposeGames | + | + | — |
| Wizer.me | + | + | — |
В результате сравнения сетевых сервисов по указанным критериям для создания интерактивного тренажера был выбран сервис Wizer.me, который позволяет создавать уникальные рабочие листы для практики.
- подбор корней уравнения;
- составление системы уравнений для данного многочлена;
- представление многочленов через основные симметрические многочлены путем равносильных преобразований;
- составление уравнения по данным системы, уравнения которой являются основными симметрическими многочленами.
Задания для отработки указанных выше умений были заложены в тренажер.
После создания тренажера проводилась его апробация, которая позволила оценить соответствие продукта поставленным критериям. Тренажер был предложен для апробации ученикам 10 класса.
В результате опроса также выяснилось, что после выполнения заданий тренажера ученики готовы применять полученные знания при решении заданий ЕГЭ и олимпиадных задач, а сам тренажер был для них полезен и интересен.
Данная глава была посвящена практической части данного проекта. В первую очередь было проведено сравнение нескольких сетевых сервисов и выбран один, наиболее соответствующий обозначенным ранее критериям. Далее были выделены основные умения, задания для отработки которых были вложены в тренажер. Затем была проведена апробация созданного продукта, и сделаны выводы о соответствии созданного тренажера заданным критериям.
В данной работе были исследованы уравнения 3 и 4 степени и способы их решения. Также были рассмотрены универсальные методы решения уравнений n степени.
Для углубления знаний в исследуемой теме были проанализированы несколько учебников, изучен рад математических статей. После обобщения полученной информации были составлены основные алгоритмы решения уравнений n степени. Так были выполнены поставленные задачи.
В ходе работы над проектом были рассмотрены способы применения теоремы Виета в решении уравнений n степени, рассмотрены различные уравнения и задачи, цель проекта достигнута.
Отдельно рассматривалось применение теоремы Виета в решении уравнений и задач. Был создан интерактивный тренажер, который позволяет ученикам самостоятельно разобраться в описываемой теме. Таким образом, гипотеза проекта подтверждена.
В ходе работы над практической составляющей проекта был создан интерактивный тренажер, который позволяет всем желающим разобраться и попрактиковаться в рассматриваемой теме. Создание такого общедоступного, информативного, удобного в использовании тренажера позволяет решить выявленную ранее проблему.
Подводя краткий итог описываемой теме, стоит сказать, что формулы Виета незаслуженно забываются людьми при решении уравнений. Хочется отметить, что теорема Виета действительно является незаменимой для решения уравнений разных степеней.
http://spacemath.xyz/teorema-vieta/
http://tvorcheskie-proekty.ru/node/3641