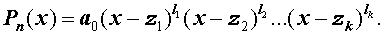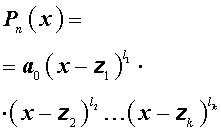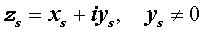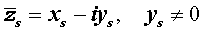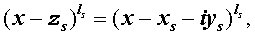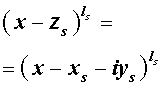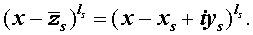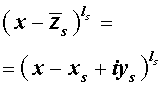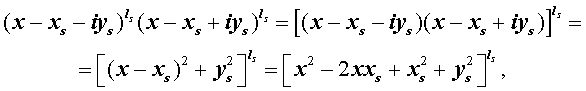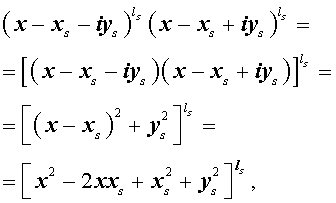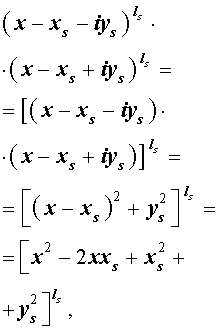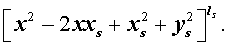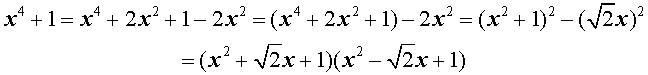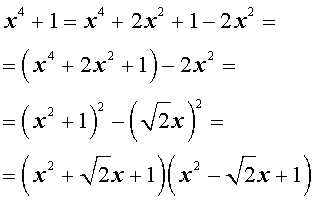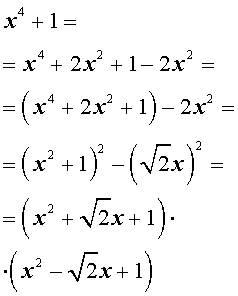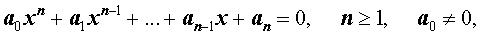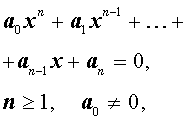Разложение многочленов на множители. Формулы Виета
 Алгебраические уравнения Алгебраические уравнения |
 Основная теорема алгебры. Разложение многочленов на линейные множители в комплексной области Основная теорема алгебры. Разложение многочленов на линейные множители в комплексной области |
 Разложение на множители многочленов с действительными коэффициентами Разложение на множители многочленов с действительными коэффициентами |
 Теорема (формулы) Виета Теорема (формулы) Виета |
Алгебраические уравнения
Пусть n – произвольное натуральное число. Рассмотрим многочлен n – ой степени от переменной x
| Pn (x) = = a0 x n + a1 x n –1 + + … + an –1 x + an , | (1) |
| a0 , a1 , … , an –1 , an | (2) |
Заметим, что в этом случае коэффициент a0 отличен от нуля, и введем следующее определение.
Определение 1 . Алгебраическим уравнением степени n с неизвестным x называют уравнение вида
| Pn (x) = 0 . | (3) |
Определение 2 . Корнем уравнения (3) называют вещественное или комплексное число α , для которого
Определение 3 . Число α называют корнем кратности k уравнения (3), если справедливо равенство
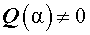
Разложение многочленов на множители в комплексной области
Основная теорема алгебры (теорема Гаусса) утверждает, что любое алгебраическое уравнение вида (3) имеет n корней, при условии, что каждый корень считается столько раз, какова его кратность.
– полный набор корней уравнения (3), а
– их кратности, то, во-первых,
а, во-вторых, справедливо равенство
Замечание . Линейными множителями называют многочлены первой степени
входящие в формулу (4), а саму формулу (4) называют формулой разложения многочленов на линейные множители в комплексной области .
Разложение на множители многочленов с действительными коэффициентами
Рассмотрим теперь многочлены степени 
Тогда справедливо следующее
Утверждение . Если комплексное число
является корнем кратности ls многочлена с вещественными коэффициентами, то и комплексно сопряженное число
является корнем этого многочлена, причем тоже кратности ls .
Из утверждения вытекает, что в разложение (4) степень каждого бинома, содержащая комплексный корень zs и имеющая вид
входит в паре со степенью бинома, содержащей комплексно сопряженный корень 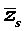
то произведение каждой пары биномов (5) и (6), входящей в формулу (4), даёт степень квадратного трехчлена с вещественными коэффициентами:
Следствие . Каждый многочлен ненулевой степени, коэффициенты которого являются вещественными числами, разлагается на множители, являющиеся многочленами с вещественными коэффициентами первой или второй степени.
Пример . Разложить на множители многочлен четвертой степени
Теорема (формулы) Виета
Снова рассмотрим уравнение n – ой степени от переменной x
и, немного изменив предыдущие обозначения, предположим, что
| z1 , z2 , … , zn –1 , zn | (8) |
— его корни, причем в записи (8) каждый корень взят столько раз, какова его кратность.
Тогда из формулы (4) вытекают следующие равенства, которые называют формулами Виета для уравнения n – ой степени :
Теорема Виета для уравнений третьей и четвертой степени
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Теорема Виета для уравнений третьей и четвертой степени Презентация по теме
Цель Научиться решать уравнения третьей и четвертой степени, используя формулы Виета.
Задачи Знакомство с научным вкладом Франсуа Виета. Вспомнить формулы Виета для приведенного квадратного уравнения. Ознакомиться с формулой для решения приведенного кубического уравнения. Ознакомиться с формулой для решения приведенного уравнения четвертой степени.
Франсуа Виет Франсуа Виет(1540—1603) — французский математик. В 1591 году ввёл буквенные обозначения не только для неизвестных величин, но и для коэффициентов уравнений; благодаря этому стало впервые возможным выражение свойств уравнений и их корней общими формулами. Ему принадлежит установление единообразного приёма решения уравнений 2-й, 3-й и 4-й степеней. В тригонометрии Франсуа Виет дал полное решение задачи об определении всех элементов плоского или сферического треугольника по трём данным.
Приведенное квадратное уравнение
Приведенное кубическое уравнение Если x1, x2, x3 – корни кубического уравнения x3 + bx2 + cx + d = 0, то
Если x1, x2, x3, x4 – корни уравнения четвертой степени x4 + bx3 + cx2 + dx + e = 0, то Приведенное уравнение четвертой степени
Вывод В данной работе мы достигли поставленных целей: я узнала о научной деятельности Ф. Виета, его вкладе в математику, ознакомилась с формулами для решения приведенных уравнений третьей и четвертой степени, мы закрепили новые знания, с помощью решения задач. Но при этом нужно отметить, что данный метод не всегда эффективен, т.к. с его помощью в некоторых ситуациях подобрать корни сложно или почти невозможно. Например: 1) x3 + 13×2 + 27x + 1 = 0 x1 = — 10,417 x2 = — 0,038 x3 = — 2,545
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 949 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 681 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 314 человек из 70 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 566 551 материал в базе
Материал подходит для УМК
«Алгебра», Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др.
§ 29. Приведённое квадратное уравнение. Теорема Виета
Другие материалы
- 16.05.2019
- 438
- 0
- 16.05.2019
- 1465
- 1
- 13.05.2019
- 6618
- 142
- 13.05.2019
- 2101
- 38
- 12.05.2019
- 557
- 39
- 10.05.2019
- 1869
- 103
- 10.05.2019
- 2636
- 50
- 30.04.2019
- 376
- 1
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 20.05.2019 3485
- PPTX 1.6 мбайт
- 82 скачивания
- Оцените материал:
Настоящий материал опубликован пользователем Семикова Наталия Геннадиевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 4 месяца
- Подписчики: 0
- Всего просмотров: 9347
- Всего материалов: 8
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Рособрнадзор не планирует переносить досрочный период ЕГЭ
Время чтения: 0 минут
Профессия педагога на третьем месте по популярности среди абитуриентов
Время чтения: 1 минута
Количество бюджетных мест в вузах по IT-программам вырастет до 160 тыс.
Время чтения: 2 минуты
ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек
Время чтения: 2 минуты
Тринадцатилетняя школьница из Индии разработала приложение против буллинга
Время чтения: 1 минута
В Воронеже продлили удаленное обучение для учеников 5-11-х классов
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Уравнения высших степеней
Вы будете перенаправлены на Автор24
Уравнения высших степеней — это уравнения, в которых старшая степень при переменной больше либо равна трём. На данный момент не существует какой-либо единой схемы для решения уравнений высших степеней.
Наиболее известными схемами для решения являются:
- Формула Кардано, он подходит только для уравнений 3-ьей степени;
- Метод Феррари для уравнений 4-ой степени;
- Теорема Виета для степени больше двух;
- Теорема Безу;
- Схема Горнера.
Ниже рассмотрены основные методы решения уравнений высших степеней с целыми и рациональными коэффициентами, справедливые для разных степеней.
Теорема Виета
Рассмотрим уравнение вида $ax^3+bx^2+cx+d=0$.
Данное уравнение обладает тремя корнями и для того чтобы его решить в общем виде, необходимо решить следующую систему:
Иначе эти системы уравнений также называют формулами Виета.
Решите уравнение: $x^3+x^2-4x-4=0$.
Решение:
Составим систему уравнений:
$\begin
Решив её, получим следующие корни:
Теорема Безу
Суть этой теоремы в том, что если уравнение вида $a_0x^n + a_1x^
Алгоритм при решении уравнения с использованием теоремы Безу следующий:
- Найти и выписать все делители свободного члена.
- Проверять эти делители до тех пор, пока не будет найден хотя бы один, являющийся корнем уравнения.
- Разделить всё уравнение на $(x-α)$ и записать само уравнение как произведение $(x-α)$ и результата выполненного деления.
- Решить полученное после разложения уравнение.
Готовые работы на аналогичную тему
Решение:
Делители члена не при переменной: $±1;±2;±3;±6$
Подставим $1$ в корень уравнения и получим, что наше равенство выполняется:
Следовательно, $x_1=1$ — один из корней уравнения. Теперь необходимо выполнить деление многочлена столбиком:
Рисунок 1. Схема деления многочлена столбиком. Автор24 — интернет-биржа студенческих работ
После этого исходное уравнение можно записать разложив на множители:
Решаем полученное квадратное уравнение и получаем ещё 2 корня: $x_<2,3>=-3;-2$.
Схема Горнера
Схема Горнера состоит в том, чтобы также сначала найти какой-либо корень уравнения вида $a_0x^n + a_1x^
После этого составляется специальная таблица с результатами деления на $(x-α)$, в которой каждый член зависим от предыдущего. Коэффициенты из данной таблицы используются как коэффициенты в полученном от деления частного многочлене, они вычисляются по формулам:
$b_0=a_0; b_1=αb_0+a_1; b_2=αb_1+a_2. b_
Рисунок 2. Таблица для вычисления коэффициентов по схеме Горнера. Автор24 — интернет-биржа студенческих работ
Решение:
Делители свободного члена — $±1;±2;±3;±6$
Запишем таблицу со коэффициентами:
Рисунок 3. Схема Горнера: пример. Автор24 — интернет-биржа студенческих работ
Отсюда получаем, что многочлен, полученный от деления на $(x-α)$ при $α=1$, равен $x^2+5x+6$.Получается, что исходное уравнение принимает вид:
Корни же второго многочлена будут $x_<2,3>=-2;-3$.
Метод одновременного подбора по коэффициенту при старшей степени и при свободном члене
Данный метод основан на следующем условии:
Несократимая дробь $\frac
$ будет корнем уравнения, если числитель этой дроби является делителем свободного члена, а знаменатель — делителем коэффициента, стоящего при члене со старшей степенью.
Алгоритм этого метода:
- Поиск делителей свободного члена.
- Поиск делителей коэффициента, стоящего при члене со старшей степенью.
- Составление дробей и подбор решения.
Решение:
Делители свободного члена: $±1; ±2; ±3; ±6$.
Делители коэффициента при старшем члене: $1; 2$.
Следовательно, как корни нужно проверить следующие значения: $1;-1;2;-2;3;-3;6;-6;\frac<1><2>; -\frac<1><2>; \frac<3><2>; -\frac<3><2>$.
Подставив эти числа в уравнения, получим, что корнями уравнения являются $x_1=1;x_2= \frac<1><2>$.
Это значит, что многочлен можно разделить на $2(x-1)(x-\frac<1><2>)=2x^2-3x+1$. При выполнении деления получаем частное $x^2+10x+6$.
Приравниваем этот многочлен к нулю и находим его корни через дискриминант, они равны $x_<3,4>=-5±\sqrt<19>$.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 14 03 2021
http://infourok.ru/teorema-vieta-dlya-uravneniy-tretey-i-chetvertoy-stepeni-3740865.html
http://spravochnick.ru/matematika/uravneniya_vysshih_stepeney/