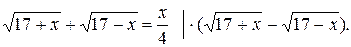Теоремы о равносильности уравнений и правила тождественных преобразований

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №19. Равносильные уравнения и неравенства

Перечень вопросов, рассматриваемых в теме

1) понятие равносильного уравнения;

2) понятие равносильного неравенства;

3) понятие уравнения-следствия;

4) основные теоремы равносильности.

Глоссарий по теме

Два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.

Если при переходе от одного уравнения к другому потери корней не происходит, то второе уравнение называет следствием первого уравнения. Иначе, если все корни первого уравнения являются корнями второго уравнения, то второе уравнения называется следствием первого уравнения.

Неравенства, имеющие одно и то же множество решений, называют равносильными. Неравенства, не имеющие решений, также являются равносильными.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Определение. Два уравнения с одной переменной

f(х) = g(х) и р(х) = h(х) называют равносильными, если множества их корней совпадают.

Иными словами, два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.

1) Уравнения равносильны, т.к. каждое из них имеет только один корень х=3.

2) Уравнения также равносильны, т.к. у них одни и те же корни .

3) А вот уравнения не равносильны, потому что у первого уравнения корень х=2, а у второго уравнения два корня х=2 и х=-2.

Из определения равносильности следует, что два уравнения равносильны, если каждый корень первого уравнения является корнем второго уравнения, и наоборот.

Решение уравнения осуществляется в три этапа.

Первый этап — технический. На этом этапе осуществляют преобразования по схеме (1) → (2) → (3)→ (4) → . и находят корни последнего (самого простого) уравнения указанной цепочки.

Второй этап — анализ решения. На этом этапе, анализируя проведенные преобразования, отвечают на вопрос, все ли они были равносильными.

Третий этап — проверка. Если анализ, проведенный на втором этапе, показывает, что некоторые преобразования могли привести к уравнению-следствию, то обязательна проверка всех найденных корней их подстановкой в исходное уравнение.

Реализация этого плана связана с поисками ответов на четыре вопроса.

• Как узнать, является ли переход от одного уравнения к другому равносильным преобразованием?
• Какие преобразования могут перевести данное уравнение в уравнение-следствие?
• Если мы в конечном итоге решили уравнение-следствие, то как сделать проверку в случае, когда она сопряжена со значительными вычислительными трудностями?
• В каких случаях при переходе от одного уравнения к другому может произойти потеря корней и как этого не допустить?

Из курса средней школы мы знаем, что можно сделать следующие преобразования уравнений: любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный.

Обе части уравнения можно умножить или разделить на одной и то же число, не равное нулю.

Если при переходе от одного уравнения к другому потери корней не происходит, то второе уравнение называет следствием первого уравнения. Иначе, если все корни первого уравнения являются корнями второго уравнения, то второе уравнения называется следствием первого уравнения.

Из этого определения и определения равносильности уравнений следует, что:

1. если ва уравнения равносильны, то каждое из них является следствием другого;
2. если каждое из двух уравнений является следствием другого, то эти уравнения равносильны.

При решении уравнений главное- не потерять корни, а наличие посторонних корней можно установить проверкой. Поэтому важно следить за тем, чтобы при преобразовании уравнения каждое следующее уравнение было следствием предыдущего.

Стоит отметить, что посторонние корни могут получиться при умножении обеих частей уравнения на выражение, содержащее неизвестное; а вот потеря корней может произойти при делении обеих частей уравнения на выражение, содержащее неизвестное.

Итак, сформулируем основные теоремы, которые используются при решении равносильных уравнений:

Определение. Областью определения уравнения f(х) = g(х) или областью допустимых значений переменной (ОДЗ) называют множество тех значений переменной х, при которых одновременно имеют смысл выражения

Теорема 1. Если какой-либо член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному.

Теорема 2. Если обе части уравнения возвести в одну и туже нечетную степень, то получится уравнение, равносильное данному.

Теорема 3. Показательное уравнение (где а > 0, a≠1)

равносильно уравнению f(x) = g(х).

Теорема 4. Если обе части уравнения f(x) = g(х) умножить на одно и то же выражение h(х), которое:

а) имеет смысл всюду в области определения (в области допустимых значений) уравнения f(x) = g(х)

б) нигде в этой области не обращается в 0, то получится уравнение f(x)h(x) = g(x)h(x), равносильное данному в его ОДЗ.

Следствием теоремы 4: если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Теорема 5. Если обе части уравнения f(x)=g(х) неотрицательны в ОДЗ уравнения, то после возведения обеих его частей в одну и ту же четную степень n получится уравнение равносильное данному в его ОДЗ.

Краткая запись теорем 4, 5.

4. f(x) = g(x) ⇔h(x)f(x) = h(x)g(x), где h(x) ≠0

и h(x) имеет смысл в ОДЗ данного уравнения.

5. f(x) = g(x) ⇔ , где f(x)≥0, g(x)≥0

и n=2k (чётное число).

Например, х – 1 = 3; х = 4

Умножим обе части на (х – 2):

(х – 2)(х – 1) = 3(х – 2); х = 4 и х = 2 – посторонний корень⇒ проверка!

Равносильность неравенств с неизвестным определяется аналогично.

Неравенства, имеющие одно и то же множество решений, называют равносильными. Неравенства, не имеющие решений, также являются равносильными.

Разбор решения заданий тренировочного модуля

Решим уравнение:

Возведем в квадрат обе части уравнения, получим:

, которое не будет равносильно исходному уравнению, потому что у этого уравнения два корня , а у первоначального уравнения только один корень х=4.

1. Неравенства и x-3 x-1 не равносильны, так как решениями первого являются числа x 1, а решениями второго- числа x>-1. При решении неравенств обычно данное неравенство преобразуется в ему равносильное.

Равносильные уравнения, преобразование уравнений

Некоторые преобразования позволяют нам перейти от решаемого уравнения к равносильным, а также к уравнениям-следствиям, благодаря чему упрощается решение первоначального уравнения. В данном материале мы расскажем, что из себя представляют эти уравнения, сформулируем основные определения, проиллюстрируем их наглядными примерами и поясним, как именно осуществляется вычисление корней исходного уравнения по корням уравнения-следствия или равносильного уравнения.

Понятие равносильных уравнений

Равносильными называются такие уравнения, имеющие одни и те же корни, или же те, в которых корней нет.

Определения такого типа часто встречаются в различных учебниках. Приведем несколько примеров.

Уравнение f ( x ) = g ( x ) считается равносильным уравнению r ( x ) = s ( x ) , если у них одинаковые корни или у них обоих нет корней.

Уравнения с одинаковыми корнями считаются равносильными. Также ими считаются два уравнения, одинаково не имеющие корней.

Если уравнение f ( x ) = g ( x ) имеет то же множество корней, что и уравнение p ( x ) = h ( x ) , то они считаются равносильными по отношению друг к другу.

Когда мы говорим о совпадающем множестве корней, то имеем в виду, что если определенное число будет корнем одного уравнения, то оно подойдет в качестве решения и другому уравнению. Ни одно из уравнений, являющихся равносильными, не может иметь такого корня, который не подходит для другого.

Приведем несколько примеров таких уравнений.

Например, равносильными будут 4 · x = 8 , 2 · x = 4 и x = 2 , поскольку каждое из них имеет только один корень – двойку. Также равносильными будут x · 0 = 0 и 2 + x = x + 2 , поскольку их корнями могут быть любые числа, то есть множества их решений совпадают. Также равносильными будут уравнения x = x + 5 и x 4 = − 1 , каждое из которых не имеет ни одного решения.

Для наглядности рассмотрим несколько примеров неравносильных уравнений.

К примеру, таковыми будут x = 2 и x 2 = 4 , поскольку их корни отличаются. То же относится и к уравнениям x x = 1 и x 2 + 5 x 2 + 5 , потому что во втором решением может быть любое число, а во втором корнем не может быть 0 .

Определения, данные выше, подойдут и для уравнений с несколькими переменными, однако в том случае, когда мы говорим о двух, трех и более корнях, более уместно выражение «решение уравнения». Таким образом, подытожим: равносильные уравнения – это те уравнения, у которых одни и те же решения или их совсем нет.

Возьмем примеры уравнений, которые содержат несколько переменных и являются равносильными друг другу. Так, x 2 + y 2 + z 2 = 0 и 5 · x 2 + x 2 · y 4 · z 8 = 0 включают в себя по три переменных и имеют только одно решение, равное 0 , во всех трех случаях. А пара уравнений x + y = 5 и x · y = 1 равносильной по отношению друг к другу не будет, поскольку, например, значения 5 и 3 подойдут для первого, но не будут решением второго: при подстановке их в первое уравнение мы получим верное равенство, а во второе – неверное.

Понятие уравнений-следствий

Процитируем несколько примеров определений уравнений-следствий, взятых из учебных пособий.

Следствием уравнения f ( x ) = g ( x ) будет уравнение p ( x ) = h ( x ) при условии, что каждый корень первого уравнения будет в то же время корнем второго.

Тождественные преобразования и равносильность уравнений

Т.Е. Бондаренко

ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ В ПРОЦЕССЕ РЕШЕНИЯ

УРАВНЕНИЙ

Учебное пособие по элементарной математике

Воронеж

УДК 512.3(075.8)

ББК 22.141.я7

Р е ц е н з е н т ы:

кандидат педагогических наук, почётный профессор кафедры информатики и методики преподавания математики (ВГПУ) Э.С. Беляева;

кандидат педагогических наук, доцент кафедры информатики и методики преподавания математики (ВГПУ) С.А. Титоренко

Бондаренко Т. Е.

Тождественные преобразования в процессе решения уравнений: учебное пособие по элементарной математике. – Воронеж: НАУКА – ЮНИПРЕСС, 2012. – 59с.

Настоящее учебное пособие посвящено использованию тождественных преобразований в процессе решения уравнений различных видов. Предметом исследования являются преобразования, изменяющие область определения уравнения, и, как следствие, приводящие к появлению посторонних корней или к их потере. Приводится анализ каждого преобразования, и рассматриваются средства, позволяющие сохранить равносильность уравнений. В книге содержатся многочисленные примеры решения уравнений, а также задания для самостоятельной работы учащихся.

Пособие предназначено для обеспечения курса элементарной математики в педагогическом вузе. Оно может быть использовано учителями средних общеобразовательных учреждений в процессе обучения математике, для подготовки учащихся к единому государственному экзамену или для проведения элективного курса в условиях профильного обучения.

© Бондаренко Т. Е., 2012

Содержание

I. Тождественные преобразования и равносильность уравнений . . . . . . 6

II.Тождественные преобразования, изменяющие область определения

1. Приведение подобных слагаемых . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

1.1. Анализ преобразования. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

1.2. Комплекс заданий.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10

2. Сокращение дробей. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

2.1. Анализ преобразования. . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11

2.2. Комплекс заданий. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .14

3. Преобразования корней арифметических корней . . . . . . . . . . . . . . . 15

3.1. Анализ преобразований. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

3.2. Комплекс заданий. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32

4. Преобразования логарифмов. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35

4.1. Анализ преобразований. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35

4.2. Комплекс заданий. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44

5. Преобразование тригонометрических выражений. . . . . . . . . . . . . . . 46

5.1. Анализ преобразований . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46

5.2. Комплекс заданий. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51

Приложение. Основные понятия и теоремы . . . . . . . . . . . . . . . . . . . . . . . 53

Предисловие

Изучение математики тесно связано с решением уравнений. Этот процесс иногда приводит к удивительным результатам. Казалось бы решение выполнено верно, но имеющийся в учебнике ответ не совпадает с полученным. Приведём примеры.

Решим уравнение (1) [2, № 5.110, с. 87]. Умножим обе части данного уравнения на сопряжённое выражение .

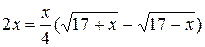
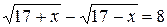
Получим уравнение (2). Очевидно, что х = 0 – корень уравнения (2). Приведём его к виду и сложим с данным уравнением (1), тогда получим уравнение , решая которое найдём корни х = -8, х = 8. Подстановкой в данное уравнение убеждаемся, что -8, 0, 8 — посторонние корни данного уравнения.

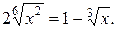
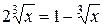
Рассмотрим ещё один пример. Решим уравнение Используя свойство арифметических корней, получим уравнение , имеющее корень Однако очевидно, что и число -1 является потерянным корнем данного уравнения.

Таким образом, иногда решение уравнения может привести к появлению посторонних корней или к их потере. Возникает вопрос, почему это происходит? В настоящем пособии приводится подробный ответ на этот вопрос для случая, когда выполняются тождественные преобразования выражений, входящих в данное уравнение. В нём перечислены преобразования, выполнение которых может привести к изменениям множества корней уравнения, и описаны средства, позволяющие сохранить его. Пособие содержит многочисленные примеры с решениями и упражнения для самостоятельной работы учащихся.

Уравнения, в которых могут появиться посторонние решения или происходит их потеря представлены в различных литературных источниках. Некоторые из них приведены в списке литературы. Особенно интересные задания включены из книг [1], [2], [3]. Однако отличительной особенностью данного пособия является его тематическая направленность и систематизация учебного материала.

Автор выражает благодарность рецензентам Э.С.Беляевой, С.А Титоренко за участие в совершенствовании пособия и надеется, что оно послужит повышению качества математической подготовки студентов и школьников.

Тождественные преобразования и равносильность уравнений

Решение данного уравнения – это процесс, состоящий в переходе к другим уравнениям до тех пор, пока не будет получено уравнение с очевидными корнями. Такие переходы осуществляются посредством различных преобразований. При этом одни преобразования приводят к уравнению с такими же корнями (равносильному данному), другие — не обладают таким свойством. Напомним, что два уравнения f₁(x)=g₁(x) и f₂(x)=g₂(x) называются равносильными (эквивалентными) на множестве М, если они имеют одни и те же решения, принадлежащие этому множеству. Преобразования, сохраняющие решения, изучаются в теории равносильных уравнений. Основное содержаниеэтой теории составляют теоремы, гарантирующие замену данного уравнения ему равносильным. Наряду с основными понятиями они приведены в приложении к настоящему курсу (с.49). Особый интерес представляет для нас теорема 1. Приведём её формулировку: если в уравнении f₁(x)=g₁(x) выполнить тождественное преобразование выражений f₁(x) или (и) g₁(x), по формуле, не меняющей область определения данного уравнения D, то получится уравнение f₂(x)=g₂(x), равносильное данному уравнению на множестве D.

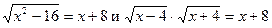
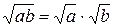
Например, в соответствии с теоремой 1 уравнения х 3 +3х 2 — 4х-12=0и(х+3)(х-2)(х+2)=0 равносильны на множестве всех действительных чисел, а уравнения не равносильны, так как х=-5, являясь корнем первого уравнения, не является корнем второго уравнения. Причина нарушения равносильности состоит в том, что в результате выполненного преобразования по формуле изменилась (сузилась) область определения данного уравнения, что привело к потере корня.

Докажем теорему 1 учитывая, что каждое уравнение вида f(x)=g(x) может быть приведено к виду F(x)=0.

Дано: уравнение F₁(x) = 0 (1) с областью определения D,

р – формула (тождество), посредством которого выполняется преобразование выражения F₁(x), не изменяющая D,

F₂(x) = 0 (2) – уравнение, полученное из данного уравнения в результате преобразования.

Доказать: уравнения (1) и (2) равносильны.

Пусть х₁ – корень уравнения (1), тогда x₁ÎD и F₁(x₁) = 0 – истинное числовое равенство. В результате применения тождества р выражение F₁(x) примет вид F₂(x). Область определения D не изменилась, то есть F₂(x₁) имеет смысл. По определению тождественно равных выражений F₂(x₁) = F₁(x₁), то есть F₂(x₁) = 0 – истинное числовое равенство, следовательно, x₁ – корень уравнения (2).

Обратно. Пусть х₂ – корень уравнения (2), тогда x₂ÎD и F₂(x₂) = 0 – истинное числовое равенство. В результате применения тождества р выражение F₂(x) примет вид F₁(x). Область определения D не изменилась, то есть F₁(x₂) имеет смысл. По определению тождественно равных выражений F₁(x₂) = 0 – истинное числовое равенство, что означает x₂ – корень уравнения (1). Равносильность доказана.

Таким образом, с преобразованиями, не изменяющими области определения данного уравнения, ситуация ясна. Однако открытым остаётся вопрос, как действовать, если тождественное преобразование меняет область определения данного уравнения. При этом оно может расширить её, и тогда возможны посторонние корни, либо сузить, что может привести к потере корней.

Выявим и исследуем тождественные преобразования, обладающие свойством расширять или сужать область определения уравнения, и определим для них средства сохранения равносильности уравнений.