ТЕМА 1. Парная линейная регрессия.
Аналитический метод выбора функциональной зависимости сводится к попытке выяснения содержательного смысла зависимости изучаемого показателя от объясняющего фактора и последующего выбора на этой основе соответствующей функциональной зависимости.
Временной (динамический) ряд (time-seriesdata) — выборка, в которой важны не только сами наблюдаемые значения, но и порядок их следования друг за другом. Чаще всего данные представляют собой наблюдения одной и той же величины в последовательные моменты времени.
Выборочная остаточная дисперсия — статистика, которая является несмещенной оценкой теоретической остаточной дисперсии σ 2 и определяется формулой
Выборочный коэффициент парной корреляции определяется по формуле
где 
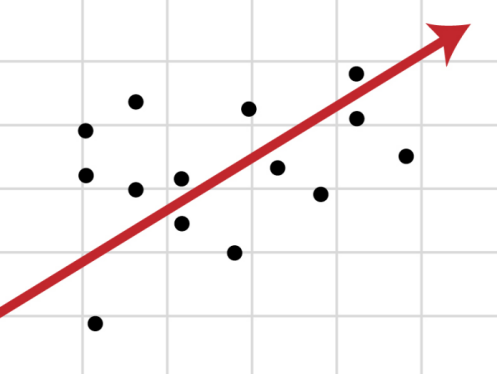
Геометрический метод выбора функциональной зависимости сводится к следующему. На координатной плоскости Oxy наносятся точки (xi,yi), i=1. n, соответствующие выборке. Полученное графическое изображение называется полем корреляции (диаграммой рассеяния).
Достоверным событием называется некоторое событие, которое обязательно происходит в условиях данного эксперимента.
Задача эконометрического моделирования: На основании экспериментальных данных определить (оценить) объясненную часть зависимой переменной и, рассматривая случайную составляющую как случайную величину, получить оценки параметров ее распределения.
Коэффициент детерминации определяется по формуле:
Величина коэффициента детерминации представляет собой долю вариации зависимой переменной, обусловленную вариацией объясняющей переменной.
Метод наименьших квадратов (МНК). Согласно методу наименьших квадратов значения параметров функции 

где минимум ищется по параметрам a, b, которые входят в зависимость 
Модель линейной парной регрессии — y=α+βx+ε.
Объясняющие переменные (факторы) — переменные (факторы) от которых зависят зависимые (объесняемые) переменные.
Основная задача эконометрического моделирования — построение по выборке эмпирической модели, выборочной парной регрессии 


Основные этапы эконометрического моделирования и анализа:
- Постановочный — формируется цель исследования (анализ экономического объекта, прогноз его показателей, имитация развития, выработка управленческих решений), теоретическое обоснование выбора переменных;
- Априорный — анализ сущности изучаемого объекта, формирование и формализация имеющейся информации;
- Параметризация — выбор вида модели (вида функции f(X)), анализ взаимосвязей и спецификация модели;
- Информационный — сбор необходимой статистической информации — наблюдаемых значений переменных;
- Идентификация модели — статистический анализ модели и оценка ее параметров;
- Верификация модели — проверка адекватности, статистической значимости модели.
Оценка теоретическое регрессии линейной парной регрессии 

Оценками неизвестных параметров регрессии по методу наименьших квадратов (оценками МНК) называются значения параметров a и b, которые минимизируют сумму квадратов отклонений выборочных значений уi от значений 
Пространственная выборка (cross-sectional data) — набор экономических показателей, полученных в некоторый момент времени (или в относительно небольшом промежутке времени), т. е. набор независимых выборочных данных из некоторой генеральной совокупности (так как практически независимость случайных величин проверить трудно, то обычно за независимые принимаются величины, не связанные причинно);
Спецификация модели — формулировка исходных предпосылок и ограничений, выбор структуры уравнения модели, представление в математической форме обнаруженных взаимосвязей и соотношений, установление состава объясняющих переменных.
Средняя ошибка аппроксимации регрессии по формуле определяется по формуле:
Значение этой ошибки в пределах 5-7% свидетельствует о хорошем соответствии модели эмпирическим данным.
Статическая (стохастическая, вероятностная) зависимость — форма связи между переменными величинами, когда каждому значению одной переменной соответствует не какое-то определенное значение другой переменной, а множество возможных значений (более точно — некоторое условное распределение) другой переменной.
Теорема Гаусса-Маркова . Если регрессионная модель y=α+βx+ε удовлетворяет условиям Гаусса-Маркова, то оценки МНК a и b имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.
Теоретическое уравнение регрессии — EX(y)=f(X), где f(X) — теоретическая функция регрессии.
Уравнение регрессионной модели — y= EX(y)+ε
- Величины εi являются случайными.
- Математическое ожидание возмущений равно нулю: E(εi)=0.
- Возмущения εi и εj некоррелированы: E(εiεj)=0, i ≠ j.
- Дисперсия возмущения εi постоянна для каждого i: D(εi)=σ 2 . Это условие называется условием гомоскедастичности. Нарушение этого условия называется гетероскедастичностью.
- Величины εi взаимно независимы со значениями объясняющих переменных.
Здесь, во всех условиях i=1,2. n.
Эконометрика — это раздел математики, занимающийся разработкой и применением статистических методов для измерений взаимосвязей между экономическими переменными.
Эконометрическая модель — y=f(X)+ε, y — зависимая переменная, X=(x1,x2. xk) — объясняющие переменные, f(X) — объясненная часть, ε — случайная составляющая (возмущение или ошибка).
Эмпирическое уравнение регрессии (модельная функция регрессии) — y=f(X,B).
Эмпирический метод выбора функциональной зависимости состоит в следующем. Выбирается некоторая параметрическая функциональная зависимость f(x).
ТЕМА 2. Множественная линейная регрессия.
Выборочная остаточная дисперсия — статистика, вычисляемая по правилу 
Выборочный коэффициент частной корреляции (частный коэффициент корреляции) между зависимыми переменными xi и xj используется для оценки взаимосвязи этих переменных, «очищенной» от влияния других факторов (см. § 2.4).
Качественный признак — признак, имеющий несколько значений.
Классическая нормальная линейная модель множественной регрессии
Модель множественной линейной регрессии Y=Xβ+ε, удовлетворяющая условиям Гаусса-Маркова, называется классической нормальной линейной моделью множественной регрессии , в предположении, что ε — нормально распределенный случайный вектор.
Коэффициент детерминации (множественный) является мерой адекватности регрессионной модели и определяется по формуле 



Коэффициент эластичности (частный коэффициент эластичности) 
Ловушкой фиктивных переменных называют ситуацию, когда сумма фиктивных переменных тождественно равна константе.
Модель множественной линейной регрессии имеет вид yi=α+β1xi1+. +βkxik+ε, 

Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных. Мультиколлинеарность может проявляться в двух формах: функциональной и стохастической.
Оценками неизвестных параметров α, β1, β2. βk линейной множественной регрессии по методу наименьших квадратов (оценками МНК) называются значения параметров a,b1,b2. bk, минимизирующие сумму квадратов отклонений выборочных значений уi от расчетных значений 
Правило введения фиктивных переменных: если качественный признак имеет p альтернативных значений (градаций), то число бинарных фиктивных переменных должно быть равно p-1.
Регрессионные уравнения с переменной структурой — модели, в которых качественные признаки существенно влияют на структуру линейных связей между переменными.
Скорректированный (исправленный) коэффициент детерминации определяется формулой: 
Стандартизованный коэффициент регрессии 

Стандартная ошибка ma коэффициента a вычисляется по правилу 

Стандартная ошибка коэффициента bi вычисляется по правилу 
Стохастическая (неполная, несовершенная) форма мультиколлинеарности имеет место в случае, когда хотя бы между двумя объясняющими переменными имеется достаточно высокая степень корреляции.
Если выполнены условия Гаусса-Маркова, то оценки метода наименьших квадратов параметров модели линейной множественной регрессии являются наиболее эффективными (в смысле минимума дисперсии линейных комбинаций оценок параметров) в классе линейных несмещенных оценок.
Фиктивная (искусственная) переменная — переменная, описывающая количественным образом различные состояния качественного признака.
Функциональная (полная, совершенная) форма мультиколлинеарности — форма мультиколлинеарности, при которой, по крайней мере, между двумя объясняющими переменными существует линейная зависимость.
Эконометрическая модель множественной регрессии — y=f(x1,x2. xk)+ε, где f(x1,x2. xk) — неизвестная функциональная зависимость (теоретическая регрессия); ε — случайное слагаемое (возмущение), представляющее собой совокупное действие не включенных в модель факторов, ошибки измерения.
Эмпирическая (выборочная) множественная линейная регрессия имеет вид: 
Эмпирическая (выборочная) регрессия 
ТЕМА 3. Гетероскедастичность и автокоррелированность остатков.
Под автокорреляцией (сериальной, последовательной корреляцией) понимается корреляция между наблюдаемыми показателями, упорядоченными определенным образом.
Автокорреляция первого порядка — тип автокорреляции, для которого наибольшее влияние на наблюдение оказывает результат предыдущего наблюдения.
Гетероскедастичности условие — условие непостоянства дисперсий возмущений.
Гомоскедастичности условие — условие постоянства дисперсий возмущений.
Классическая регрессионная модель
Модель множественной линейной регрессии Y=Xβ+ε, удовлетворяющая условиям Гаусса-Маркова, называется классической регрессионной моделью .
Коэффициент автокорреляции первого порядка — парный коэффициент корреляции между рядами e1, e2. en-1 и e2, e3. en, вычисляемый по формуле 
Лаговые переменные — факторы, влияние которых характеризуется определенным запаздыванием.
Модели с гетероскедастичностью — регрессионные модели, для которых дисперсии возмущений не одинаковы.
Модели с корреляцией ошибок — регрессионные модели, для которых наблюдаемые значения зависимой переменной коррелируют со значениями в предыдущие моменты времени, т.е. имеет место корреляция между различными возмущениями.
Обобщенная линейная модель множественной регрессии имеет вид Y=Xβ+ε, где переменые Y — вектор зависимых переменных размера (nx1), X — (nxk) матрица объясняющих переменных, β — (kx1) вектор параметров регрессии, ε — (nx1) вектор случайных возмущений, причем предполагаются выполненными условия:
- Вектор возмущений ε=(ε1. εn) является случайным вектором.
- E(ε)=0n (0n — нулевой вектор размера n).
- Σε= E(εε T )=Ω, где Ω — положительно определнная матрица.
- Величины εi взаимно независимы со значениями объясняющих переменных.
- r(X)=k+1.
Обобщенный метод наименьших квадратов (ОМНК) — способ оценивания вектора коэффициентов регрессионного уравнения, при котором оценка зависит от матрицы ковариации ошибок.
Отрицательная автокорреляция имеет место, если r(εt-1,εt) Положительная автокорреляция имеет место, если r(εt-1,εt)>0.
Статистика Дарбина-Уотсона используется в тесте Дарбина-Уотсона для оценки корреляции остатков и вычисляется
В классе линейных несмещенных оценок вектора β для обобщенной регрессионной модели оценка 
Тест Дарбина-Уотсона является критерием обнаружения автокорреляции первого порядка (см. §3.3.1).
Тест Голдфелда-Квандта позволяет определить наличие гетероскедастичности (см. §3.2.2).
Тест ранговой корреляции Спирмена позволяет определить наличие гетероскедастичности (см. §3.2.1).
ТЕМА 4. Нелинейные модели и их линеаризация.
Абсолютная ошибка аппроксимации используется для оценки качества нелинейной регрессии и вычисляется следующим образом:
Двойная логарифмическая модель — линейная модель, в которой и зависимая и объясняющая переменные заданы в логарифмической виде 
Индекс корреляции используется для оценки качества нелинейной регрессии и вычисляется следующим образом:
Коэффициент эластичности характеризует влияние фактора на зависимую переменную и вычисляется по формуле 
Линейно логарифмические (полулогарифмические) модели — нелинейные по объясняющим переменным, но линейные по оцениваемым параметрам модели, имеющие вид: 
Логарифмически линейная (логлинейная) модель — нелинейная модель вида lny= α+βx+ε.
Модель с квадратными корнями — нелинейная по объясняющим переменным, но линейная по оцениваемым параметрам модель, имеющая вид: 
Обратная (гиперболическая) модель — нелинейная по объясняющим переменным, но линейная по оцениваемым параметрам модель, имеющая вид: 
Показательная (экспоненциальная) модель — нелинейная модель вида y=αe βx ε.
Полиномиальная модель — нелинейная по объясняющим переменным, но линейная по оцениваемым параметрам модель, имеющая вид:
Среднее абсолютное отклонение используется для оценки качества нелинейной регрессии и вычисляется следующим образом:
Стандартная ошибка регрессии (среднее квадратическое отклонение) используется для оценки качества нелинейной регрессии и вычисляется следующим образом:
Степенная модель — нелинейная по объясняющим переменным, но линейная по оцениваемым параметрам модель, имеющая вид:
ТЕМА 5. Системы линейных уравнений.
Двухшаговый метод наименьших квадратов – метод построения оценок структурных коэффициентов, основанный на методе инструментальных переменных (см. §5.2).
Идентифицируемость – возможность определения структурных коэффициентов уравнения по коэффициентам приведенной формы.
Идентифицируемое уравнение – уравнение, все входящие структурные параметры которого идентифицируемы.
Идентифицируемый параметр – структурный параметр, который может быть однозначно оценен с помощью косвенного метода наименьших квадратов.
Инструментальные переменные – новые переменные, которые тесно коррелируют с исходными регрессорами и не коррелируют со случайными составляющими.
Косвенный метод наименьших квадратов – метод построения оценок структурных коэффициентов с помощью оценок коэффициентов приведенной формы (см. §5.1).
Лагированные переменные (эндогенные переменные с лагом) — эндогенные переменные, относящиеся к предыдущим моментам времени.
Метод инструментальных переменных – один из самых распространенных методов оценивания уравнений, в которых регрессоры коррелируют со случайными компонентами (см. §5.2).
Неидентифицируемый параметр – структурный параметр, значение которого нельзя определить, даже зная точные значения параметров приведенной формы.
Предопределенными переменными называют экзогенные переменные и эндогенные переменные с лагом.
Приведенная форма системы одновременных уравнений – разрешенная относительно эндогенных переменных система уравнений в структурной форме, в правых частях новых уравнений которой останутся только экзогенные переменные:
Порядковые условия – необходимые условия, используемые для проверки идентифицируемости структурных уравнений (см. §5.3).
Сверхидентифицируемый параметр – структурный параметр, которому косвенный метод наименьших квадратов дает несколько различных его оценок, то есть существует несколько значений структурного коэффициента, соответствующих найденным значениям приведенных коэффициентов.
Система линейных одновременных уравнений записывается таким образом, что в левых частях уравнений будут выделены эндогенные переменные, рассматриваемые как объясняемые переменные, в правой части будет представлена зависимость этих переменных от экзогенных переменных и оставшихся эндогенных.
Структурная форма системы линейных одновременных уравнений имеет вид
то есть, эндогенных переменных в такой системе столько же, сколько и уравнений, но в отдельном уравнении их может быть несколько. В каждом уравнении, взятом в отдельности, только одна переменная, помещенная в левую часть, может рассматриваться как объясняемая, а остальные эндогенные переменные в этом уравнении являются регрессорами, причем коррелирующими со случайным возмущением.
Структурные параметры – параметры системы линейных одновременных уравнений, записанной в структурной форме.
Трехшаговый метод наименьших квадратов – метод построения оценок структурных коэффициентов, сочетающий процедуру одновременного оценивания и метод инструментальных переменных (см. §5.2).
Экзогенные переменные — переменные, определяемые вне системы.
Эндогенные переменные — переменные, определяемые внутри системы.
ТЕМА 6. Временные ряды.
Авторегрессионная модель скользящей средней порядков p и q соответственно имеет вид
Авторегрессионная модель p-го порядка описывает изучаемый показатель в момент t в зависимости от его значений в предыдущие моменты yt-1, yt-2. yt-p и имеет вид:
Авторегрессионные модели – модели, в которых в качестве лаговых переменных участвуют значения зависимых переменных.
Аддитивная модель временного ряда представляется в виде суммы компонент: yt=ut+st+vt+εt.
Временной (динамический) ряд – последовательность наблюдений некоторого признака, упорядоченных в порядке возрастания моментов времени.
Выборочный коэффициент автокорреляции определяется по формуле
Гипотеза случайности значений ряда наблюдений – гипотеза о независимости и стационарности распределения наблюдений, образующих временной ряд.
Коррелограмма – график выборочной автокорреляционной функции 
Критерий «восходящих и нисходящих» серий – критерий, согласно которому проверяется гипотеза случайности (см. §6.2.2).
Критерий серий, основанный на медиане выборки – критерий, согласно которому проверяется гипотеза случайности (см. §6.2.1).
Лаговые переменные — переменные, влияние которых характеризуется некоторым запаздыванием.
Метод аналитического выравнивания используется для оценки тренда и периодической составляющей временного ряда (см. §6.3).
Методы сглаживания временного ряда используются для оценки тренда и периодической составляющей временного ряда и делятся на:
- сглаживание с помощью скользящей средней (см. §6.4);
- сглаживание с помощью простой скользящей средней (см. §6.4);
- сглаживание с помощью взвешенной скользящей средней (см. §6.4);
- сглаживание с помощью скользящей медианы (см. §6.4);
- экспоненциальное сглаживание (см. §6.5).
Модели с лагами (распределенными лагами) – динамическая модели, содержащие в качестве лаговых переменных только независимые (объясняющие) переменные.
Модель скользящей средней q-го порядка имеет вид:
Мультипликативная модель временного ряда представляется в виде произведения компонент: yt=ut× st× vt× εt.
Сезонная компонента st уровней временного ряда – компонента уровней временного ряда, отражающая повторяемость экономических процессов в течение не слишком длительного периода.
Случайная компонента εt уровней временного ряда – компонента уровней временного ряда, отражающая влияние случайных, а также неучтенных факторов.
Стационарный временной ряд – временной ряд yt, вероятностные свойства которого (закон распределения yt и его числовые характеристики) не зависят от момента времени t.
Тренд ut уровней временного ряда – плавно меняющаяся компонента уровней временного ряда, отражающая влияние долговременных, систематических факторов, основную тенденцию в формировании рассматриваемого показателя.
Уровни ряда – отдельные наблюдения yt, t=1,2. n (где n – число наблюдений).
Циклическая компонента vt уровней временного ряда – компонента уровней временного ряда, отражающая повторяемость экономических процессов в течение длительных периодов.
Множественная линейная регрессия. Улучшение модели регрессии
Понятие множественной линейной регрессии
Множественная линейная регрессия — выраженная в виде прямой зависимость среднего значения величины Y от двух или более других величин X 1 , X 2 , . X m . Величину Y принято называть зависимой или результирующей переменной, а величины X 1 , X 2 , . X m — независимыми или объясняющими переменными.
В случае множественной линейной регрессии зависимость результирующей переменной одновременно от нескольких объясняющих переменных описывает уравнение или модель

где 

Функция множественной линейной регрессии для выборки имеет следующий вид:

где 

Уравнение множественной линейной регрессии и метод наименьших квадратов
Коэффициенты модели множественной линейной регресии, так же, как и для парной линейной регрессии, находят при помощи метода наименьших квадратов.
Разумеется, мы будем изучать построение модели множественной регрессии и её оценивание с использованием программных средств. Но на экзамене часто требуется привести формулы МНК-оценки (то есть оценки по методу наименьших квадратов) коэффициентов уравнения множественной линейной регрессии в скалярном и в матричном видах.
МНК-оценка коэффиентов уравнения множественной регрессии в скалярном виде
Метод наименьших квадратов позволяет найти такие значения коэффициентов, что сумма квадратов отклонений будет минимальной. Для нахождения коэффициентов решается система нормальных уравнений
Решение системы можно получить, например, методом Крамера:

Определитель системы записывается так:
МНК-оценка коэффиентов уравнения множественной регрессии в матричном виде
Данные наблюдений и коэффициенты уравнения множественной регрессии можно представить в виде следующих матриц:
Формула коэффициентов множественной линейной регрессии в матричном виде следующая:

где 


Решая это уравнение, мы получим матрицу-столбец b, элементы которой и есть коэффициенты уравнения множественной линейной регрессии, для нахождения которых и был изобретён метод наименьших квадратов.
Построение наилучшей (наиболее качественной) модели множественной линейной регрессии
Пусть при обработке данных некоторой выборки в пакете программных средств STATISTICA получена первоначальная модель множественной линейной регрессии. Предстоит проанализировать полученную модель и в случае необходимости улучшить её.
Качество модели множественной линейной регрессии оценивается по тем же показателям качества, что и в случае модели парной линейной регрессии: коэффициент детерминации 

Важный показатель качества модели линейной регрессии — проверка на выполнение требований Гаусса-Маркова к остаткам. В качественной модели линейной регрессии выполняются все условия Гаусса-Маркова:
- условие 1: математическое ожидание остатков равно нулю для всех наблюдений ( ε(e i ) = 0 );
- условие 2: теоретическая дисперсия остатков постоянна (равна константе) для всех наблюдений ( σ²(e i ) = σ²(e i ), i = 1, . n );
- условие 3: отсутствие систематической связи между остатками в любых двух наблюдениях;
- условие 4: отсутствие зависимости между остатками и объясняющими (независимыми) переменными.
В случае выполнения требований Гаусса-Маркова оценка коэффициентов модели, полученная методом наименьших квадратов является
Затем необходимо провести анализ значимости отдельных переменных модели множественной линейной регрессии с помощью критерия Стьюдента.
В случае наличия резко выделяющихся наблюдений (выбросов) нужно последовательно по одному исключить их из модели и проанализировать наличие незначимых переменных в модели и, в случае необходимости исключить их из модели по одному.
В исследованиях поведения человека, как и во многих других, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.
Кроме того, требуется на основе тех же данных построить две нелинейные модели регрессии — с квадратами двух наиболее значимых переменных и с логарифмами тех же наиболее значимых переменных. Они также будут сравниваться с линейными моделями, полученных на разных шагах.
Также требуется построить модели с применением пошаговых процедур включения (FORWARD STEPWISE) и исключения (BACKWARD STEPWISE).
Все полученные модели множественной регрессии нужно сравнить и выбрать из них наилучшую (наиболее качественную). Теперь разберём перечисленные выше шаги последовательно и на примере.
Оценка качества модели множественной линейной регрессии в целом
Пример. Задание 1. Получено следующее уравнение множественной линейной регрессии:
и следующие показатели качества описываемой этим уравнением модели:
 | adj. | RSS | SEE | F | p-level |
| 0,426 | 0,279 | 2,835 | 1,684 | 2,892 | 0,008 |
Сделать вывод о качестве модели в целом.
Ответ. По всем показателям модель некачественная. Значение 

Для анализа на выполнение условий Гаусса-Маркова воспользуемся диаграммой рассеивания наблюдений (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши):
Результаты проверки графика показывают: условие равенства нулю математического ожидания остатков выполняется, а условие на постоянство дисперсии — не выполняется. Достаточно невыполнения хотя бы одного условия Гаусса-Маркова, чтобы заключить, что оценка коэффициентов модели линейной регрессии не является несмещённой, эффективной и состоятельной.
Анализ значимости коэффициентов модели множественной линейной регрессии
С помощью критерия Стьюдента проверяется гипотеза о том, что соответствующий коэффициент незначимо отличается от нуля, и соответственно, переменная при этом коэффициенте имеет незначимое влияние на зависимую переменную. В свою очередь, в колонке p-level выводится вероятность того, что основная гипотеза будет принята. Если значение p-level больше уровня значимости α, то основная гипотеза принимается, иначе – отвергается. В нашем примере установлен уровень значимости α=0,05.
Пример. Задание 2. Получены следующие значения критерия Стьюдента (t) и p-level, соответствующие переменным уравнения множественной линейной регрессии:
| Перем. | Знач. коэф. | t | p-level |
| X1 | 0,129 | 2,386 | 0,022 |
| X2 | -0,286 | -2,439 | 0,019 |
| X3 | -0,037 | -0,238 | 0,813 |
| X4 | 0,15 | 1,928 | 0,061 |
| X5 | 0,328 | 0,548 | 0,587 |
| X6 | -0,391 | -0,503 | 0,618 |
| X7 | -0,673 | -0,898 | 0,375 |
| X8 | -0,006 | -0,07 | 0,944 |
| X9 | -1,937 | -2,794 | 0,008 |
| X10 | -1,233 | -1,863 | 0,07 |
Сделать вывод о значимости коэффициентов модели.
Ответ. В построенной модели присутствуют коэффициенты, которые незначимо отличаются от нуля. В целом же у переменной X8 коэффициент самый близкий к нулю, а у переменной X9 — самое высокое значение коэффициента. Коэффициенты модели линейной регрессии можно ранжировать по мере убывания незначимости с возрастанием значения t-критерия Стьюдента.
Исключение резко выделяющихся наблюдений
Пример. Задание 3. Выявлены несколько резко выделяющихся наблюдений (выбросов, то есть наблюдений с нетипичными значениями): 10, 3, 4 (соответствуют строкам исходной таблицы данных). Эти наблюдения следует последовательно исключить из модели и по мере исключения заполнить таблицу с показателями качества модели. Исключили наблюдение 10 — заполнили значение показателей, далее исключили наблюдение 3 — заполнили и так далее. По мере исключения STATISTICA будет выдавать переменные, которые остаются значимыми в модели множественной линейной регрессии — они будут выделены красном цветом. Те, что не будут выделены красным цветом — незначимые переменные и их также нужно внести в соответствующую ячейку таблицы. По завершении исключения выбросов записать уравнение конечной множественной линейной регрессии.
| № | adj. | SEE | F | p- level | незнач. пер. |
| 10 | 0,411 | 2,55 | 2,655 | 0,015 | X3, X4, X5, X6, X7, X8, X10 |
| 3 | 0,21 | 2,58 | 2,249 | 0,036 | X3, X4, X5, X6, X7, X8, X10 |
| 4 | 0,16 | 2,61 | 1,878 | 0,082 | X3, X4, X5, X6, X7, X8, X10 |
Уравнение конечной множественной линейной регрессии:
Случается однако, когда после исключения некоторого наблюдения исключение последующих наблюдений приводит к ухудшению показателей качества модели. Причина в том, что с исключением слишком большого числа наблюдений выборка теряет информативность. Поэтому в таких случаях следует вовремя остановиться.
Исключение незначимых переменных из модели
Пример. Задание 4. По мере исключения из модели множественной линейной регрессии переменных с незначимыми коэффициентами (получены при выполнении предыдущего задания, занесены в последнюю колонку таблицы) заполнить таблицу с показателями качества модели. Последняя колонка, обозначенная звёздочкой — список переменных, имеющих значимое влияние на зависимую переменную. Эти переменные STATISTICA будет выдавать выделенными красным цветом. По завершении исключения незначимых переменных записать уравнение конечной множественной линейной регрессии.
| Искл. пер. | adj. | SEE | F | p- level | * |
| X3 | 0,18 | 1,71 | 2,119 | 0,053 | X4, X5, X6, X7, X8, X10 |
| X4 | 0,145 | 1,745 | 1,974 | 0,077 | X5, X6, X7, X8, X10 |
| X5 | 0,163 | 2,368 | 2,282 | 0,048 | X6, X7, X8, X10 |
| X6 | 0,171 | 2,355 | 2,586 | 0,033 | X7, X8, X10 |
| X7 | 0,167 | 2,223 | 2,842 | 0,027 | X8, X10 |
| X8 | 0,184 | 1,705 | 3,599 | 0,013 | X10 |
Когда осталась одна переменная, имеющая значимое влияние на зависимую переменную, больше не исключаем переменные, иначе получится, что в модели все переменные незначимы.
Уравнение конечной множественной линейной регрессии после исключения незначимых переменных:
Переменные X1 и X2 в задании 3 не вошли в список незначимых переменных, поэтому они вошли в уравнение конечной множественной линейной регрессии «автоматически».
Нелинейные модели для сравнения
Пример. Задание 5. Построить две нелинейные модели регрессии — с квадратами двух наиболее значимых переменных и с логарифмами тех же наиболее значимых переменных.
Так как в наблюдениях переменных X9 и X10 имеется 0, а натуральный логарифм от 0 вычислить невозможно, то берутся следующие по значимости переменные: X1 и X2.
Полученное уравнение нелинейной регрессии с квадратами двух наиболее значимых переменных:
Показатели качества первой модели нелинейной регрессии:
 | adj. | RSS | SEE | F | p-level |
| 0,17 | 0,134 | 159,9 | 1,845 | 4,8 | 0,0127 |
Вывод: модель некачественная, так как RSS и SEE принимают высокие значения, p-level стремится к нулю, коэффициент детерминации незначимо отличается от нуля.
Полученное уравнение нелинейной регрессии с логарифмами двух наиболее значимых переменных:
Показатели качества второй модели нелинейной регрессии:
 | adj. | RSS | SEE | F | p-level |
| 0,182 | 0,148 | 157,431 | 1,83 | 5,245 | 0 |
Вывод: модель некачественная, так как RSS и SEE принимают высокие значения, p-level стремится к нулю, коэффициент детерминации незначимо отличается от нуля.
Применение пошаговых алгоритмов включения и исключения переменных
Пример. Задание 6. Настроить пакет STATISTICA для применения пошаговых процедур включения (FORWARD STEPWISE) и исключения (BACKWARD STEPWISE). Для этого в диалоговом окне MULTIPLE REGRESSION указать Advanced Options (stepwise or ridge regression). В поле Method выбрать либо Forward Stepwise (алгоритм пошагового включения), либо Backward Stepwise (алгоритм пошагового исключения). Необходимо настроить следующие параметры:
- в окне Tolerance необходимо установить критическое значение для уровня толерантности (оставить предложенное по умолчанию);
- в окне F-remove необходимо установить критическое значение для статистики исключения (оставить предложенное по умолчанию);
- в окне Display Results необходимо установить режим At each step (результаты выводятся на каждом шаге процедуры).
Построить, как описано выше, модели множественной линейной регрессии автоматически.
В результате применения пошагового алгоритма включения получено следующее уравнение множественной линейной регрессии:
Показатели качества модели нелинейной регрессии, полученной с применением пошаговой процедуры включения:
 | adj. | RSS | SEE | F | p-level |
| 0,41 | 0,343 | 113,67 | 1,61 | 6,11 | 0,002 |
В результате применения пошагового алгоритма исключения получено следующее уравнение множественной линейной регрессии:
Показатели качества модели нелинейной регрессии, полученной с применением пошаговой процедуры исключения:
 | adj. | RSS | SEE | F | p-level |
| 0,22 | 0,186 | 150,28 | 1,79 | 6,61 | 0 |
Выбор самой качественной модели множественной линейной регрессии
Пример. Задание 7. Сравнить модели, полученные на предыдущих шагах и определить самую качественную.
| Модель | Ручная | Кв. перем. | Лог. перем. | forward stepwise | backward stepwise |
 | 0,255 | 0,17 | 0,182 | 0,41 | 0,22 |
adj. | 0,184 | 0,134 | 0,148 | 0,343 | 0,186 |
| RSS | 122,01 | 159,9 | 157,43 | 113,67 | 150,28 |
| SEE | 1,705 | 1,845 | 1,83 | 1,61 | 1,79 |
| F | 3,599 | 4,8 | 5,245 | 6,11 | 6,61 |
| p-level | 0,013 | 0,0127 | 0 | 0,002 | 0 |
Самая качественная модель множественной линейной регрессии — модель, построенная методом FORWARD STEPWISE (пошаговое включение переменных), так как коэффициент детерминации у неё самый высокий, а RSS и SEE наименьшие в сравнении значений оценок качества других регрессионных моделей.
R — значит регрессия
Статистика в последнее время получила мощную PR поддержку со стороны более новых и шумных дисциплин — Машинного Обучения и Больших Данных. Тем, кто стремится оседлать эту волну необходимо подружится с уравнениями регрессии. Желательно при этом не только усвоить 2-3 приемчика и сдать экзамен, а уметь решать проблемы из повседневной жизни: найти зависимость между переменными, а в идеале — уметь отличить сигнал от шума.
Для этой цели мы будем использовать язык программирования и среду разработки R, который как нельзя лучше приспособлен к таким задачам. Заодно, проверим от чего зависят рейтинг Хабрапоста на статистике собственных статей.
Введение в регрессионный анализ
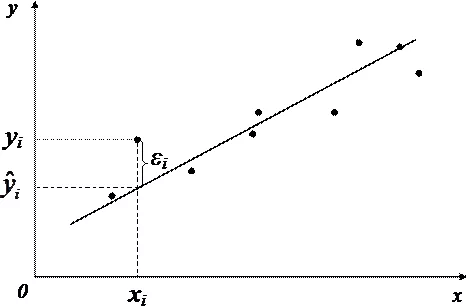
Если имеется корреляционная зависимость между переменными y и x , возникает необходимость определить функциональную связь между двумя величинами. Зависимость среднего значения
называется регрессией y по x .
Основу регрессионного анализа составляет метод наименьших квадратов (МНК), в соответствии с которым в качестве уравнения регресии берется функция такая, что сумма квадратов разностей
минимальна.
Карл Гаусс открыл, или точнее воссоздал, МНК в возрасте 18 лет, однако впервые результаты были опубликованы Лежандром в 1805 г. По непроверенным данным метод был известен еще в древнем Китае, откуда он перекочевал в Японию и только затем попал в Европу. Европейцы не стали делать из этого секрета и успешно запустили в производство, обнаружив с его помощью траекторию карликовой планеты Церес в 1801 г.
Вид функции , как правило, определен заранее, а с помощью МНК подбираются оптимальные значения неизвестных параметров. Метрикой рассеяния значений
вокруг регрессии
является дисперсия.
- k — число коэффициентов в системе уравнений регрессии.
Чаще всего используется модель линейной регрессии, а все нелинейные зависимости приводят к линейному виду с помощью алгебраических ухищрений, различных преобразования переменных y и x .
Линейная регрессия
Уравнения линейной регрессии можно записать в виде
В матричном виде это выгладит
- y — зависимая переменная;
- x — независимая переменная;
- β — коэффициенты, которые необходимо найти с помощью МНК;
- ε — погрешность, необъяснимая ошибка и отклонение от линейной зависимости;
Случайная величина может быть интерпретирована как сумма из двух слагаемых:
— полная дисперсия (TSS).
— объясненная часть дисперсии (ESS).
— остаточная часть дисперсии (RSS).
Еще одно ключевое понятие — коэффициент корреляции R 2 .
Ограничения линейной регрессии
Для того, чтобы использовать модель линейной регрессии необходимы некоторые допущения относительно распределения и свойств переменных.
- Линейность, собственно. Увеличение, или уменьшение вектора независимых переменных в k раз, приводит к изменению зависимой переменной также в k раз.
- Матрица коэффициентов обладает полным рангом, то есть векторы независимых переменных линейно независимы.
- Экзогенность независимых переменных —
. Это требование означает, что математическое ожидание погрешности никоим образом нельзя объяснить с помощью независимых переменных.
- Однородность дисперсии и отсутствие автокорреляции. Каждая εi обладает одинаковой и конечной дисперсией σ 2 и не коррелирует с другой εi. Это ощутимо ограничивает применимость модели линейной регрессии, необходимо удостовериться в том, что условия соблюдены, иначе обнаруженная взаимосвязь переменных будет неверно интерпретирована.
Как обнаружить, что перечисленные выше условия не соблюдены? Ну, во первых довольно часто это видно невооруженным глазом на графике.
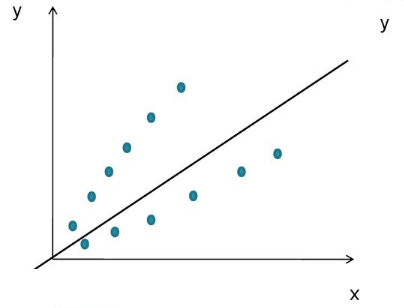
Неоднородность дисперсии
При возрастании дисперсии с ростом независимой переменной имеем график в форме воронки.
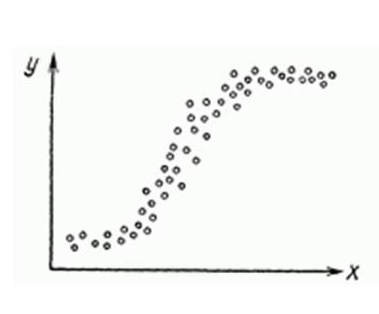
Нелинейную регрессии в некоторых случая также модно увидеть на графике довольно наглядно.
Тем не менее есть и вполне строгие формальные способы определить соблюдены ли условия линейной регрессии, или нарушены.
- Автокорреляция проверяется статистикой Дарбина-Уотсона (0 ≤ d ≤ 4). Если автокорреляции нет, то значения критерия d≈2, при позитивной автокорреляции d≈0, при отрицательной — d≈4.
- Неоднородность дисперсии — Тест Уайта,
, при
\chi<^2>_<\alpha;m-1>$» data-tex=»inline»/> нулевая гипотеза отвергается и констатируется наличие неоднородной дисперсии. Используя ту же
можно еще применить тест Бройша-Пагана.
- Мультиколлинеарность — нарушения условия об отсутствии взаимной линейной зависимости между независимыми переменными. Для проверки часто используют VIF-ы (Variance Inflation Factor).
В этой формуле — коэффициент взаимной детерминации между
и остальными факторами. Если хотя бы один из VIF-ов > 10, вполне резонно предположить наличие мультиколлинеарности.
Почему нам так важно соблюдение всех выше перечисленных условий? Все дело в Теореме Гаусса-Маркова, согласно которой оценка МНК является точной и эффективной лишь при соблюдении этих ограничений.
Как преодолеть эти ограничения
Нарушения одной или нескольких ограничений еще не приговор.
- Нелинейность регрессии может быть преодолена преобразованием переменных, например через функцию натурального логарифма ln .
- Таким же способом возможно решить проблему неоднородной дисперсии, с помощью ln , или sqrt преобразований зависимой переменной, либо же используя взвешенный МНК.
- Для устранения проблемы мультиколлинеарности применяется метод исключения переменных. Суть его в том, что высоко коррелированные объясняющие переменные устраняются из регрессии, и она заново оценивается. Критерием отбора переменных, подлежащих исключению, является коэффициент корреляции. Есть еще один способ решения данной проблемы, который заключается в замене переменных, которым присуща мультиколлинеарность, их линейной комбинацией. Этим весь список не исчерпывается, есть еще пошаговая регрессия и другие методы.
К сожалению, не все нарушения условий и дефекты линейной регрессии можно устранить с помощью натурального логарифма. Если имеет место автокорреляция возмущений к примеру, то лучше отступить на шаг назад и построить новую и лучшую модель.
Линейная регрессия плюсов на Хабре
Итак, довольно теоретического багажа и можно строить саму модель.
Мне давно было любопытно от чего зависит та самая зелененькая цифра, что указывает на рейтинг поста на Хабре. Собрав всю доступную статистику собственных постов, я решил прогнать ее через модель линейно регрессии.
Загружает данные из tsv файла.
- points — Рейтинг статьи
- reads — Число просмотров.
- comm — Число комментариев.
- faves — Добавлено в закладки.
- fb — Поделились в социальных сетях (fb + vk).
- bytes — Длина в байтах.
Вопреки моим ожиданиям наибольшая отдача не от количества просмотров статьи, а от комментариев и публикаций в социальных сетях. Я также полагал, что число просмотров и комментариев будет иметь более сильную корреляцию, однако зависимость вполне умеренная — нет надобности исключать ни одну из независимых переменных.
Теперь собственно сама модель, используем функцию lm .
В первой строке мы задаем параметры линейной регрессии. Строка points
. определяет зависимую переменную points и все остальные переменные в качестве регрессоров. Можно определить одну единственную независимую переменную через points
reads , набор переменных — points
Перейдем теперь к расшифровке полученных результатов.
- Intercept — Если у нас модель представлена в виде
, то тогда
— точка пересечения прямой с осью координат, или intercept .
- R-squared — Коэффициент детерминации указывает насколько тесной является связь между факторами регрессии и зависимой переменной, это соотношение объясненных сумм квадратов возмущений, к необъясненным. Чем ближе к 1, тем ярче выражена зависимость.
- Adjusted R-squared — Проблема с
в том, что он по любому растет с числом факторов, поэтому высокое значение данного коэффициента может быть обманчивым, когда в модели присутствует множество факторов. Для того, чтобы изъять из коэффициента корреляции данное свойство был придуман скорректированный коэффициент детерминации .
- F-statistic — Используется для оценки значимости модели регрессии в целом, является соотношением объяснимой дисперсии, к необъяснимой. Если модель линейной регрессии построена удачно, то она объясняет значительную часть дисперсии, оставляя в знаменателе малую часть. Чем больше значение параметра — тем лучше.
- t value — Критерий, основанный на t распределении Стьюдента . Значение параметра в линейной регрессии указывает на значимость фактора, принято считать, что при t > 2 фактор является значимым для модели.
- p value — Это вероятность истинности нуль гипотезы, которая гласит, что независимые переменные не объясняют динамику зависимой переменной. Если значение p value ниже порогового уровня (.05 или .01 для самых взыскательных), то нуль гипотеза ложная. Чем ниже — тем лучше.
Можно попытаться несколько улучшить модель, сглаживая нелинейные факторы: комментарии и посты в социальных сетях. Заменим значения переменных fb и comm их степенями.
Проверим значения параметров линейной регрессии.
Как видим в целом отзывчивость модели возросла, параметры подтянулись и стали более шелковистыми , F-статистика выросла, так же как и скорректированный коэффициент детерминации .
Проверим, соблюдены ли условия применимости модели линейной регрессии? Тест Дарбина-Уотсона проверяет наличие автокорреляции возмущений.
И напоследок проверка неоднородности дисперсии с помощью теста Бройша-Пагана.
В заключение
Конечно наша модель линейной регрессии рейтинга Хабра-топиков получилось не самой удачной. Нам удалось объяснить не более, чем половину вариативности данных. Факторы надо чинить, чтобы избавляться от неоднородной дисперсии, с автокорреляцией тоже непонятно. Вообще данных маловато для сколь-нибудь серьезной оценки.
Но с другой стороны, это и хорошо. Иначе любой наспех написанный тролль-пост на Хабре автоматически набирал бы высокий рейтинг, а это к счастью не так.
http://function-x.ru/statistics_regression2.html
http://habr.com/ru/post/350668/