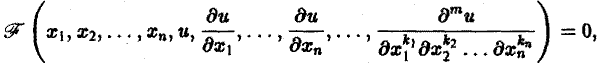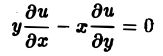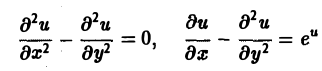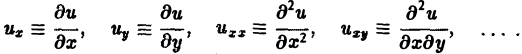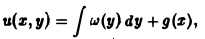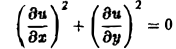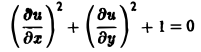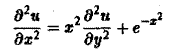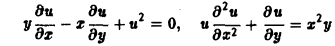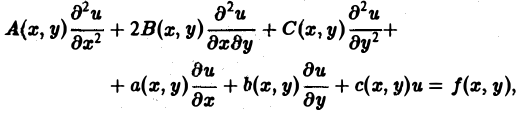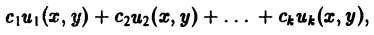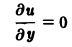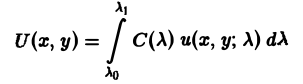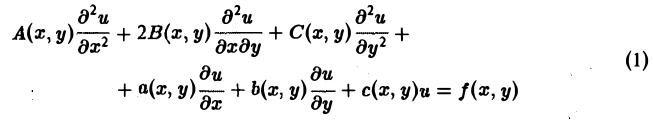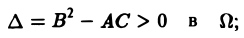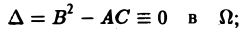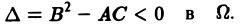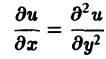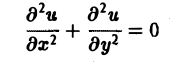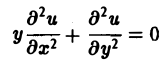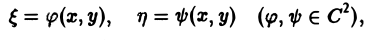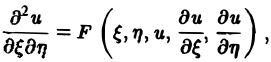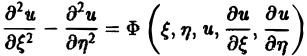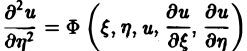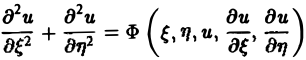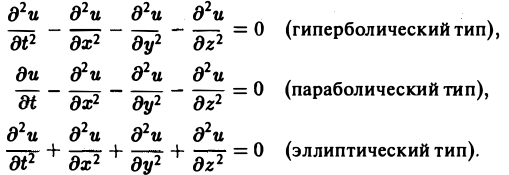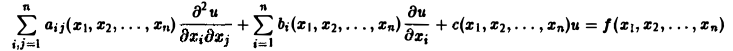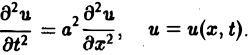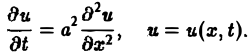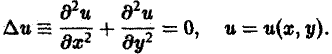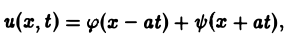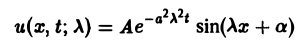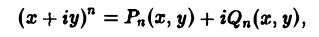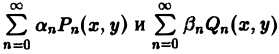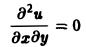Теория уравнений в частных производных

Примеры по дифференциальным уравнениям в частных производных

Немного теории

Дифференциальным уравнением с частными производными (ДУ с ЧП) называется уравнение относительно неизвестной функции нескольких переменных (ФНП) и ее частных производных. Наивысший порядок частных производных (существенно входящих в уравнение) называется порядком этого уравнения.

ДУ с ЧП называется линейным (ЛДУ с ЧП), если неизвестная функция и ее производные входят в это ДУ линейно (в первой степени).

В этом разделе вы найдете подробно решенные задачи по темам: классификация и приведение к каноническому виду ДУ с ЧП второго порядка с двумя переменными, определение типа уравнения, решение уравнений и систем ДУ в ЧП.

ДУ с ЧП находят широкое применение в прикладных науках: квантовая механика, электродинамика, термодинамика, теория теплои массопереноса и др. при математическом описании и моделировании различных физических процессов. Поэтому такие уравнения изучаются под общим названием уравнений математической физики (примеры решений 16 задач).

Приведение к каноническому виду

Задача 1. Привести к каноническому виду уравнение

Задача 2. Привести уравнение к каноническому виду.

Задача 3. Найти общее решение уравнения, приведя его к каноническому виду:

Решение ДУ в ЧП

Задача 4. Решить уравнение Пфаффа

$$ z^2 dx +zdy +(3zx +2y)dz=0. $$

Задача 5. Решить задачу Коши для уравнения в частных производных

$$ u_-2\Delta u =(x^2+y^2+z^2)t; \quad u(t=0)=xyz, u_t(t=0)=x-y. $$

Задача 6. Найти общее решение уравнения в частных производных

Задача 7. Найти общее решение уравнения в частных производных первого порядка.

$$ xy u_x +(x-2u)u_y = yu. $$

Задача 8. Найти решение задачи Коши для уравнения в частных производных

$$ y u_x -xy u_y=2xu, \quad u(x+y=2)=1/y. $$

Задача 9. Решить систему дифференциальных уравнений в частных производных

Разные задачи на исследование ДУ в ЧП

Задача 10. Найти поверхность, удовлетворяющую данному уравнению и проходящую через данную линию

Задача 11. Найти области гиперболичности, эллиптичности и параболичности уравнения и исследовать их зависимость от $l$, где $l$ – числовой параметр.

Задача 12. Найти функцию, гармоническую внутри круга радиуса $R$ c центром в начале координат и такую, что

Помощь с решением ДУ в ЧП

Если вам нужна помощь с решением задач и контрольных по дифференциальным уравнениям (и другим разделам математического анализа), обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей , оформление производится в Word, срок от 1 дня.

Теория уравнений с частными производными, Мизохата С., 1977

Теория уравнений с частными производными, Мизохата С., 1977.

Книга представляет собой написанный на высоком научном уровне учебник по уравнениям с частными производными. Она содержит изложение важнейших разделов современной теории дифференциальных уравнений. Автор широко использует аппарат функционального анализа — теорию обобщенных функций, теорию функциональных пространств и общую теорию линейных операторов. Изложение обладает рядом методических достоинств.
Книга рассчитана на студентов и аспирантов математических и физических факультетов университетов и педвузов.

Случай многих переменных. Функциональные пространства.
Результаты, полученные в предыдущих параграфах, остаются справедливыми и для случая многих переменных; это можно доказать прямыми методами. Здесь мы будем изучать случай многих переменных с помощью равенства Парсеваля, которое явится для нас источником основных идей. Ради удобства мы введем некоторые функциональные пространства, с которыми будем работать в последующих параграфах. Читатель может рассматривать их сейчас только как удобный способ обозначений; в дальнейшем, во второй главе, мы подробно изучим эти пространства, исследуя их топологическую природу. Вообще говоря, привлекая теорию топологических векторных пространств, важно подобрать эти пространства так, чтобы они обладали топологией, согласованной с природой рассматриваемых задач и наших методов их решения.

В действительности теория дифференциальных уравнений с частными производными и теория функциональных пространств тесно связаны между собой; изучение дифференциальных уравнений с частными производными требует введения новых функциональных пространств, и, обратно, теория функциональных пространств играет значительную роль в изучении дифференциальных уравнений с частными производными.

В дальнейшем мы увидим, что все рассматриваемые нами топологические пространства являются полными. Мы будем использовать обозначения, введенные в книгах Л. Шварца [1].

ОГЛАВЛЕНИЕ.
Предисловие редактора перевода.
Предисловие автора к русскому изданию.
Предисловие автора.
Глава 1. Ряды Фурье. Преобразование Фурье.
§1. Ряды Фурье.
§2. Интегралы Дирихле.
§3. Приложение к уравнению теплопроводности.
§4. Система ортогональных функций в L2.
§5. Интегральная формула Фурье.
§6. Преобразование Фурье.
§7. Случай многих переменных. Функциональные пространства.
§8. Кратные ряды Фурье.
§9. Преобразование Фурье функций нескольких переменных.
§10. Теорема Планшереля.
§11. Обобщение теоремы Планшереля.
Глава 2. Распределения.
§1. Определение распределения, сходимость последовательности распределений.
§2. Основные свойства пространств Фреше.
§3. Функциональные пространства.
§4. Структуры пространств.
§5. Преобразование Фурье распределений.
§6. Преобразования Фурье некоторых функций.
§7. Связь между преобразованием Фурье и сверткой.
§8. Преобразование Лапласа для функций.
§9. Преобразование Лапласа распределении.
§10. Преобразование Лапласа векторнозначных функций.
§11. Преобразование Фурье сферически симметричной функции.
§12. Фундаментальные решения эллиптических операторов с постоянными коэффициентами.
Глава 3. Эллиптические уравнения (общая теория).
§1. Введение.
§2. Решение задачи Дирихле (оператор Грина).
§3. Теорема Реллиха.
§4. След на границе (граничные значения в расширенном смысле).
§5. Описание пространства.
§6. Свойства пространства.
§7. Улучшение оценки для yf.
§8. Краевые задачи для эллиптического дифференциального уравнения второго порядка.
§9. Задача Дирихле для общего эллиптического уравнения второго порядка.
§10. Теорема об альтернативе Фредгольма для вполне непрерывного оператора.
§11. Дифференцируемость решений.
§12. Дифференцируемость решения в окрестности границы.
§13. Интерполяционная теорема для EmL2(Rn).
§14. Некоторые замечания о задаче Дирихле.
§15. Краевая задача третьего рода.
§16. Расширение самосопряженных операторов.
§17. Задача Дирихле для эллиптического оператора высокого порядка.
Глава 4. Задача с начальными условиями (задача Коши).
§1. Введение.
§2. Теоремы Коши — Ковалевской и Хольмгрена.
§3. Замечания о разрешимости задачи Коши.
§4. Локальная разрешимость задачи Коши.
§5. Непрерывная зависимость решения задачи Коши от начальных условий.
§6. Область зависимости.
§7. Теорема существования решений.
§8. Процессы с конечной скоростью распространения.
§9. Решение волнового уравнения.
§10. Системы гиперболических уравнений первого порядка.
Глава 5. Эволюционные уравнения.
§1. Введение.
§2. Задача Коши.
§3. Преобразование Лапласа и полугруппы.
§4. Параболические полугруппы.
§5. Полугруппы для самосопряженных операторов.
§6. Два примера параболических уравнений.
Глава 6. Гиперболические уравнения.
§1. Введение.
§2. Энергетическое неравенство для симметрической гиперболической системы.
§3. Замечания об энергетических неравенствах.
§4. Первая теорема существования решения симметрической гиперболической системы уравнений (случай, когда коэффициенты не зависят от t).
§5. Вторая теорема существования для симметрической гиперболической системы уравнений (общий случай).
§6. Несимметрические гиперболические системы.
§7. Сингулярные интегральные операторы.
§8. Свойства сингулярных интегральных операторов.
§9. Энергетическое неравенство для системы гиперболических уравнений.
§10. Энергетическое неравенство для гиперболических уравнений.
§11. Теорема существования решения для системы гиперболических уравнений.
§12. Область зависимости.
§13. Теорема существования решения для гиперболического уравнения.
§14. Единственность решения задачи Коши.
Глава 7. Почти линейные гиперболические уравнения.
§1. Введение.
§2. Оценка произведения функций.
§3. Гладкость сложной функции.
§4. Первая теорема существования (случай гиперболических систем).
§5. Вторая теорема существования (случай одного уравнения).
§6. Пример (почти линейное волновое уравнение).
Глава 8. Функции Грина и спектры.
§1. Введение.
§2. Функции Грина и компенсирующие функции.
§3. Функция Грина для оператора.
§4. Теорема Фредгольма.
§5. Построение функции Грина.
§6. Свойства функций Грина.
§7. Решение волнового уравнения во внешней области.
§8. Дискретный спектр оператора Шредннгера.
§9. Дискретный и непрерывный спектры.
§10. Расширение по Фридрихсу.
§11. Дискретный спектр.
§12. Об отрицательной части спектра.
§13. Самосопряженные расширения.
§14. Отрицательная часть спектра оператора.
Дополнительные замечания.
§1. Общие краевые задачи для эллиптических уравнений высокого порядка.
§2. Полнота системы собственных функций.
Комментарии к списку литературы.
Список литературы.
Указатель обозначений.
Предметный указатель.

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Теория уравнений с частными производными, Мизохата С., 1977 - fileskachat.com, быстрое и бесплатное скачивание.

Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России. Купить эту книгу

Дифференциальные уравнения в частных производных с примерами решения и образцами выполнения

Дифференциальным уравнением с частными производными называется уравнение вида
(1)

связывающее независимые переменные x1, х2, … , хn искомую функцию и = и(х1, х2,…, хn) и ее частные производные (наличие хотя бы одной производной обязательно). Здесь ki,k2,… ,кn — неотрицательные целые числа, такие, что к1 + к2 + … + кп = т.

Порядком дифференциального уравнения называется наивысший порядок входящие в уравнение частных производных. Так, если х, у — независимые переменные, и = и(х, у) — искомая функция, то

— дифференциальное уравнение 1-го порядка;

— дифференциальные уравнения 2-го порядка.

Для упрощения записи пользуются также следующими обозначениями:

Пусть имеем дифференциальное уравнение с частными производными (1) порядка т. Обозначим через С m (D) множество функций, непрерывных в области D вместе со всеми производными до порядка m включительно.

Определение:

Решением дифференциального уравнения (1) в некоторой области D изменения независимых переменных x1, x2…xn,. называется всякая функция и = и(х1, х2,…, xп) ∈ С m (D) такая, что подстановка этой функции и ее производных в уравнение (1) обращает последнее в тождество по x1, x2, …., хп в области D.

Пример:

Найти решение и = и(х,у) уравнения

Равенство (2) означает, что искомая функция и не зависит опт х, но может быть любой функцией от у,

u = φ(y). (3)

Таким образом, решение (3) уравнения (2) содержит одну произвольную функцию. Это — общее решение уравнения (2).

Приме:

Найти решение u = u(z, у) уравнения

Положим = о. Тогда уравнение (4) примет вид = 0. Его общим решением будет произвольная функция v = w(у). Поскольку v= приходим к уравнению = w(у). Интегрируя по у (считая х параметром), получим

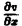
где g(x) — произвольная функция. Так как w(у) — произвольная функция, то и интеграл от нее также является произвольной функцией; обозначим его через f(у). В результате получим решение уравнения (4) в виде

u(x, y) = f(y) + g(x) (5)

произвольные дифференцируемые функции).

Решение (5) уравнения с частными производными 2-го порядка (4) содержит уже две произвольные функции. Его называют общим решением уравнения (4), так как всякое другое решение уравнения (4) может быть получено из (5) подходящим выбором функций f и g.

Мы видим, таким образом, что уравнения с частными производными имеют целые семейства решений. Однако существуют уравнения с частными производными, множества решений которых весьма узки и, в некоторых случаях, да же пусты.

Пример:

Множество действительных решений уравнения

исчерпывается функцией u(x, y) = const, а уравнение

вовсе не имеет действительных решений.

Мы не ставим пока вопрос об отыскании частных решений. Позже будет выяснено, какие дополнительные условия нужно задать, чтобы с их помощью можно было выделить частное решение, т.е. функцию, удовлетворяющую как дифференциальному уравнению, так и этим дополнительным условиям.

Линейные дифференциальные уравнения с частными производными. Свойства их решений

Уравнение с частными производными называется линейным, если оно линейно относительно искомой функции и всех ее производных, входящих в уравнение; в противном случае уравнение называется нелинейным.

Пример:

— линейное уравнение; уравнения

Линейное дифференциальное уравнение 2-го порядка для функции двух независимых переменных х, у в общем случае имеет вид
(1)

где А(х, у), В(х, у), …, с(х,у), f(x,y) — функции переменных х, у, заданные в некоторой области D плоскости хОу. Если f(x,y) ≡ 0 в D, то уравнение (1) называется однородным, в противном случае — неоднородным.

Обозначив левую часть уравнения (1) через L[u], запишем (1) в виде

L[u] = f(x, у). (2)

Соответствующее однородное уравнение запишется так:

L[u] = 0. (3)

Здесь L — линейный дифференциальный оператор, определенный на линейном пространстве C 2 (D) функций и = и(х, у).

Пользуясь свойством линейности оператора L, легко убедиться в справедливости следующих теорем, выражающих свойства решений линейных однородных дифференциальных уравнений с частными производными.

Теорема:

Если и(х, у) есть решение линейного однородного уравнения (3), то си(х, у), где с — любая постоянная, есть также решение уравнения (3).

Теорема:

Если и₁(х, у) и и₂(х, у) — решения линейного однородного уравнения (3), то сумма и₁(х, у) + и₂(x, у) есть также решение этого уравнения.

Следствие:

Если каждая из функций и₁(х, у) и и₂(х, у), u k(x, у) является решением уравнения (3), то линейная комбинация

где c1, c2 …, сk — произвольные постоянные, также является решением этого уравнения.

В отличие от обыкновенного линейного однородного дифференциального уравнения, имеющего конечное число линейно независимых частных решений, линейная

комбинация которых дает общее решение этого уравнения, уравнение с частными производными может иметь бесконечное множество линейно независимых частных решений.

Пример:

имеет общее решение k = φ(х), так что решениями его будут, например, функции 1,х,…, х n ,… . В соответствии с этим в линейных задачах для уравнений с частными производными нам придется иметь дело не только с линейными комбинациями конечного числа решений, но и с рядами 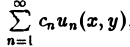, членами которых являются произведения постоянных Сп на частные решения иn(х, у) дифференциального уравнения.

Возможны случаи, когда функция и(х, у; λ) при всех значениях параметра λ из некоторого интервала (λо, λ1), конечного или бесконечного, является решением уравнения (3). В этом случае говорят, что решения уравнения зависят от непрерывно меняющегося параметра λ. Если теперь взять функцию С(λ) такую, что первые и вторые производные интеграла

по х и по у могут быть получены с помощью дифференцирования под знаком интеграла, то этот интеграл также будет решением уравнения (3). Для линейного неоднородного уравнения

L[u] = f (4)

справедливы следующие предложения.

Теорема:

Если и(х, у) есть решение линейного неоднородного уравнения (4), a v(x, у) — решение соответствующего однородного уравнения (3), то сумма и + v есть решение неоднородного уравнения (4).

Теорема:

Принцип суперпозиции. Если и1(х, у) —решение уравнения L[u] = f1, a u2(x,y) — решение уравнения L[u] = f2, то и1 + u2 — решение уравнения L[u] = f1 + f2.

Классификация линейных дифференциальных уравнений второго порядка с двумя независимыми переменными

Определение:

Линейное дифференциальное уравнение второго порядка

в некоторой области Q на плоскости хОу называется

1) гиперболическим в Ω, если

2) параболическим в Ω, если

3) эллиптическим в Ω, если

Пользуясь этим определением, легко проверить, что уравнения

— гиперболические при всех х и у, уравнение

— параболическое при всех х и у, а уравнение

— эллиптическое при всех х и у. Уравнение

— эллиптическое при у > 0, параболическое на линии у = 0 и гиперболическое в полуплоскости у

с помощью которой уравнение (1) преобразуется к более простому, каноническому виду, своему для каждого типа уравнения.

Уравнение гиперболического типа (∆ > 0) преобразуется к вшу

(два канонических вида уравнений гиперболического типа).

Уравнение параболического типа (∆ ≡ 0) преобразуется к виду

(канонический вид уравнения параболического типа).

Уравнение эллиптического типа (∆

(канонический вид уравнения эллиптического типа). Здесь F и Ф — некоторые функции, зависящие от искомой функции и, ее первых производных 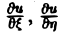и независимых переменных ξ, η. Вид функций F и Ф определяется исходным уравнением (1).

В некоторых случаях каноническая форма уравнения позволяет найти общее решение исходного уравнения.

Как правило, приведениеуравнения(1) к каноническому виду путем замены независимых переменных имеет локальный характер, т. е. осуществимо лишь в некоторой достаточно малой окрестности рассматриваемой точки Mo(xo, уo).

Когда число п независимых переменных больше двух, также различают уравнения гиперболического, параболического и эллиптического типов. Например, при п = 4 простейшая каноническая форма таких уравнений имеет вид

Здесь и = и(х, у, z, t).

Замечание:

В общем случае, когда число независимых переменных больше двух, приведение линейною уравнения с переменными коэффициентами

к каноническому виду возможно только в данной точке 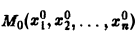и невозможно в любой сколь угодно малой окрестности этой точки.

Мы ограничимся рассмотрением линейных дифференциальных уравнений 2-го порядка. К таким уравнениям приводит большое количество различных физических задач.

Так, колебательные процессы различной природы (колебания струн, мембран, акустические колебания газа в трубах, электромагнитные колебания и т. д.) описываются уравнениями гиперболического типа. Простейшим из таких уравнений является уравнение колебаний струны (одномерное волновое уравнение): (2)

Здесь х — пространственная координата, t — время, 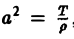где Т — натяжение струны, р — ее линейная плотность.

Процессы теплопроводности и диффузии приводят к уравнениям параболического типа. В одномерном случае простейшее уравнение теплопроводности имеет вид
(3)

Здесь 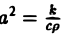где р — плотность среды, с — удельная теплоемкость, k — коэффициент теплопроводности.

Наконец, установившиеся процессы, когда искомая функция не зависит от времени, определяются уравнениями эллиптического типа, типичным представителем которых является уравнение Лапласа
(4)

Непосредственной проверкой убеждаемся в том, что решением уравнения (2) является всякая функция и(х, t) вида

Можно показать, что решениями уравнения (3) являются функции вида

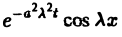
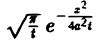
произвольные постоянные, А — числовой параметр). Интегрируя решение и(х, t; λ) = уравнения (3) по параметру λ в пределах от — ∞ до + ∞ , получим так называемое фундаментальное решение U(x, t) = уравнения теплопроводности.

Наконец, нетрудно убедиться, что действительнозначные функции Рn(х,у) и Qn(x, у), определяемые из соотношения

являются решениями уравнения Лапласа (4) для п = 0, 1, 2…..Этот последний результат есть частный, случай общего утверждения, что и действительная и мнимая части аналитической функции

f(z) = u(x, у) + iv(x, у)

комплексного переменного z = х + iy являются решениями уравнения Лапласа (4).

В силу линейности уравнения (4) ряды

тоже будут решениями уравнения (4), если они сходятся равномерно, как и ряды, полученные из них двукратным почленным дифференцированием по каждому из аргументов х, у.

Таким образом, для простейшей — канонической — формы уравнений гиперболического, параболического и эллиптического типов мы располагаем о решениях этих уравнений некоторой информацией.

Постановка основных задач для линейных дифференциальных уравнений второго порядка

Для полного описания того или иного физического процесса мало иметь только дифференциальное уравнение процесса, надо еще задать начальное состояние этого процесса (начальные условия) и режим на границе S той области Ω, в которой процесс происходит (граничные условия). Это обусловлено неединственностью решения дифференциальных уравнений.

Пример:

Общее решение уравнения

имеет вид и(х, у) = f(x) + g(y), где f(x) и g(y) — произвольные дифференцируемые функции. Поэтому чтобы выделить решение, описывающее данный физический процесс, необходимо задать дополнительные условия.

Различают три основных типа задач для дифференциальных уравнений с частными производными (число независимых переменных равно п):

а) задача Коши для уравнений гиперболического и параболического типов: задаются начальные условия, область Ω совпадает со всем пространством R n , граничные условия отсутствуют;

б) краевая задача для уравнений эллиптического типа: задаются граничные условия на границе S области Ω, начальные условия отсутствуют;

в) смешанная задача для уравнений гиперболического и параболического типов: задаются начальные и граничные условия, Ω ≠ R n

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института