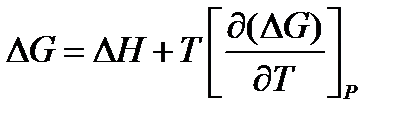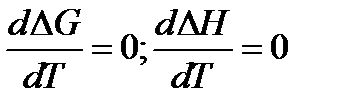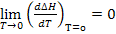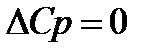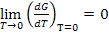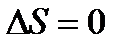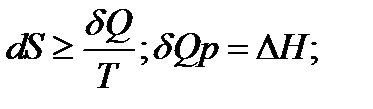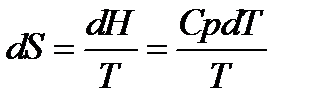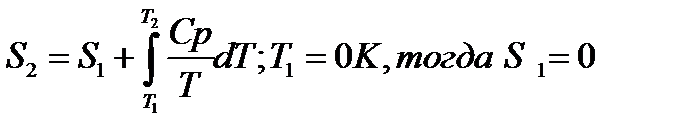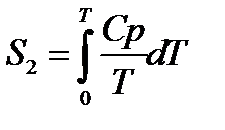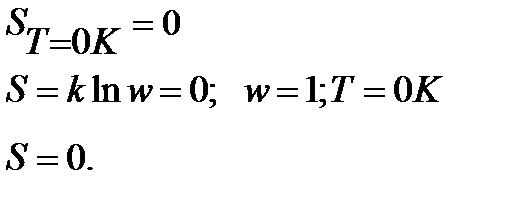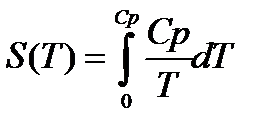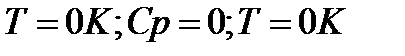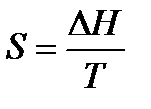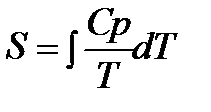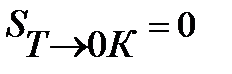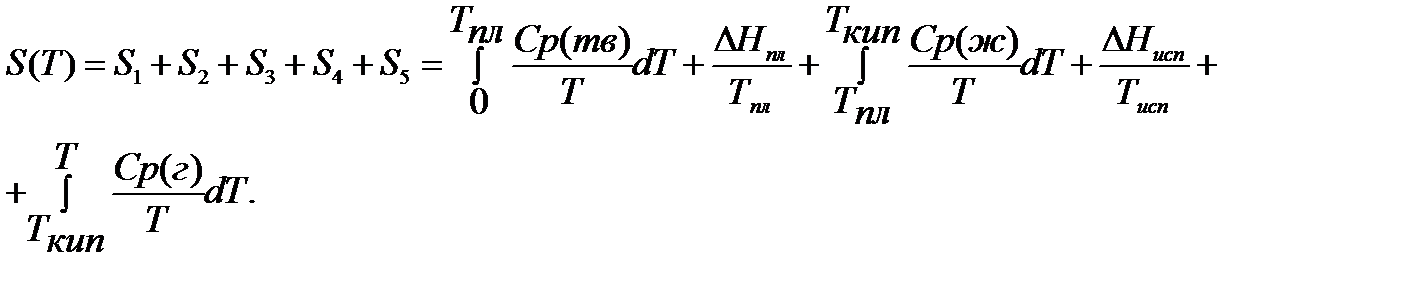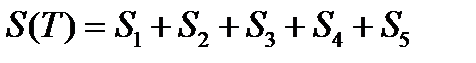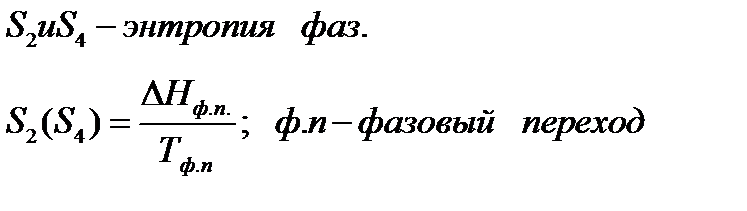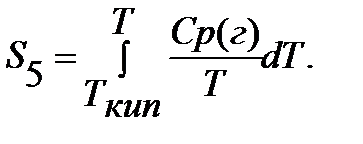Тепловая теорема нернста вывод уравнения нернста

Тепловая теорема Нернста и следствия из неё

Недостаточность первого и второго законов термодинамики

Для расчёта химических равновесий

На основании первого и второго законов термодинамики были получены уравнения для расчёта ΔG 0 и К_Р:

ΔG = — T + TI (5.1)

lnK_P = + i (5.2)

Однако для расчёта стандартного химического сродства или константы равновесия химической реакции помимо термических данных, а именно теплового эффекта реакции и температурных зависимостей теплоёмкостей участников реакции, необходимо знать постоянные интегрирования I и i. Эти постоянные интегрирования придают неопределённость уравнениям. Неопределённость уравнения (5.1) наглядно иллюстрируется на рисунке 5.1:

— —зависимость ΔН = f(T);

—— — зависимость ΔG =f(Т)

Рисунок 5.1 — Зависимость ΔG = f(T) и ΔН = f(T)

в области низких температур.

Ход кривой ΔН =f(T) явно определяется из термических данных, определение которых не представляет особых трудностей. Ход кривой ΔG =f(T) зависит от значения выбранной постоянной интегрирования I. Константа не может быть выбрана произвольно. Она имеет строго определённое значение, при которой кривая ΔG =f(T) соответствует данной зависимости ΔН= f(T). На основании первого и второго законов термодинамики невозможно теоретическим путём рассчитать постоянную интегрирования. Именно в этом заключается недостаточность первого и второго законов термодинамики для расчёта химических равновесий. Уравнениями (5.1) и (5.2) можно воспользоваться для расчёта константы равновесия только в том случае, если известны хотя бы при одной температуре величины ΔG или K_P.Эти величины при какой либо температуре могут быть определены только экспериментальным путём.

Тепловая теорема Нернста и следствия из неё

Исследуя тепловые явления вблизи абсолютного нуля, В.Нернст сделал предположение, что кривые ΔG = f(T) и ΔH = f(T) не только исходят из одной точки при Т=0, К, но и имеют общую касательную, параллельную оси температур. Это предположение получило название тепловой теоремы Нернста. Тепловая теорема Нернста позволяет ликвидировать неопределённость в уравнении (5.1). Действительно, из семейства кривых ΔG =f(T) необходимо выбрать только одну, которая имеет общую касательную к кривой ΔH = f(T), параллельную оси температур (рисунок 5.2):

— —зависимость ΔН = f(T);

—— — зависимость ΔG =f(Т)

Рисунок 5.2 — Положение кривых ΔG = f(T) и ΔН = f(T)

в соответствии с тепловой теоремой Нернста.

Математически тепловую теорему Нернста можно представить в виде уравнения:

= = 0 (5.3)

Из тепловой теоремы Нернста вытекает ряд следствий:

1) Из свойств G как характеристической функции следует, что

(5.4)

Тогда из тепловой теоремы Нернста вытекает, что если Т 0, К, то для любой химической реакции справедливо:

Это означает, что все химическое реакции вблизи абсолютного нуля протекают без изменения энтропии.

2)Зависимость теплового эффекта химической реакции от температуры в дифференциальной форме имеет вид:

= ΔС_Р (5.6)

Из тепловой теоремы следует, что при Т 0, К = 0, тогда

Это означает, что в области температур близкой к абсолютному нулю все химические реакции протекают без теплообмена с окружающей средой. Тепловой эффект химических реакций в этих условиях не будет зависеть от температуры.

3) Зависимость теплового эффекта химической реакции от температуры имеет вид:

ΔН = ΔН₀ + Δ Т + Т 2 – Δс’T -1 (5.8)

Продифференцируем уравнение (5.8) по температуре:

= 0 + Δ + Т – T -2 (5.9)

При Т=0, К все члены уравнения (5.9), содержащие Т, равны нулю. Поскольку, согласно тепловой теореме Нернста, при Т 0, К отношение = 0, то

Δ = 0 (5.10)

4) Зависимость энергии Гиббса химической реакции от температуры имеет вид:

ΔG = ΔH — Δ TlnT — T 2 — Т -1 +TI (5.11)

С учётом того, что = 0, получим:

ΔG = ΔH₀ – T 2 — Т -1 + TI (5.12)

Продифференцируем уравнение (5.12) по температуре:

= 0 + Т + Т -2 + I (5.13)

При Т = 0, К все члены уравнения (5.11), содержащие Т, равны нулю. Кроме того, из тепловой теоремы Нернста следует, что при Т=0, К = 0,

Таким образом, из тепловой теоремы Нернста вытекает, что Δ = 0 и I = 0.

С учётом этого уравнение для расчёта стандартного изменения энергии Гиббса для химической реакции будет иметь вид:

ΔG = ΔH₀ — T 2 — Т -1 (5.15)

Уравнение (5.15) позволяет рассчитывать ΔG , а, следовательно, и константу равновесия химической реакции только на основании термических данных или, другими словами, на основании теплового эффекта химической реакции и зависимости теплоёмкостей участников реакции от температуры. Тем самым, ликвидируется недостаточность первого и второго законов термодинамики для расчёта химических равновесий. Недостатком уравнения (5.15) является то, что оно пригодно для расчётов только в области низких температур.

Постулат Планка. Третий закон термодинамики

Из тепловой теоремы Нернста следует, что вблизи абсолютного нуля все химические реакции в конденсированных фазах протекают без изменения энтропии. Планк расширил это заключение, распространив его на абсолютную энтропию реагирующих веществ. Он выдвинул постулат, что энтропия любого индивидуального бездефектного кристаллического вещества (идеального кристалла) при абсолютном нуле равна нулю:

S = 0 (5.16)

Уравнение (5.16) представляет собой математическую формулировку третьего закона термодинамики.

Своё обоснование третий закон термодинамики получает в статистической термодинамике, основное уравнение которой имеет вид:

где k – постоянная Больцмана;

W – термодинамическая вероятность.

При постепенном охлаждении величина термодинамической вероятности уменьшается и достигает своего минимально значения, т. е. единицы, при абсолютном нуле. Тогда

S = k·lnW = k·ln = 0 (5.18)

Уравнение (5.18) согласуется с постулатом Планка. С точки зрения статистической теории энтропия идеального кристалла может быть равна нулю только при условии W = , т.е. когда данное макросостояние может быть осуществлено единственным микросостоянием. Во всех остальных случаях энтропия кристаллического вещества при абсолютном нуле должна быть больше нуля.

ТРЕТИЙ ЗАКОН ТЕРМОДИНАМИКИ. ТЕПЛОВАЯ ТЕОРИЯ НЕРНСТА

Ранее нами были рассмотрены способы определения внутренней энергии и энтальпии, а также расчеты энергий Гиббса и Гельмгольца. Теперь остановимся на возможности расчета энтропии. Подобная возможность возникает после ознакомления с третьим законом термодинамики. Его следует рассматривать в качестве постулата о предельном значении энтропии и ее изменениях в процессах, происходящих вблизи абсолютного нуля температуры.

Существует несколько формулировок III закона термодинамики:

1. Постулат Планка

Энтропия любого термодинамически равновесного процесса при абсолютном нуле температуры равна нулю;

2. Абсолютный нуль температур не достижим (принцип недостижимости нуля температуры);

3. По мере приблежения к абсолютному нулю значения энтальпии ∆H и энергия ∆G сближаются (тепловая теорема Нернста).

ТЕПЛОВАЯ ТЕОРЕМА НЕРНСТА

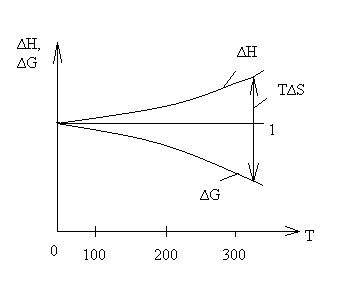
Тепловая теорема Нернста показывает, что по мере приближения к абсолютному нулю происходит сближение между энтальпией ∆Н и энергией Гиббса ∆G, а при абсолютном нуле сближаются кривые, характеризующие изменение ∆Н и ∆G от температуры, и образующаяся общая касательная 1 параллельна оси температуры.

3.

1- Общая касательная

Теорема Нернста: Вблизи абсолютного нуля первая производная по температуре энергии Гиббса равна первой производной изменения энтальпии и равна нулю.

Следствие:

1. ;

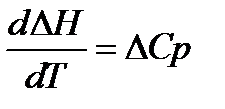
Теплоёмкость вещества при абсолютном нуле температуры равна нулю.

2. ;

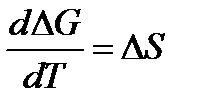
Изменение энтропии при абсолютном нуле температуры равно нулю.

При этом наблюдется так называемое явление «вырождение», когда по мере приближения к абсолютному нулю свойства тел все меньше зависят от температуры.

Обратимся к формуле 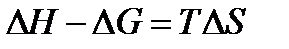, т.е. в соответствии с тепловой теоремой Нернста разность между кривыми ∆Н и ∆G есть Т∆S. При этом Т → 0 изменение энтропии, согласно 2 следствию теоремы Нернста, становится близким к нулю, и кривые начинают сходиться.

Расширенная формулировка Планка

При изменение температуры от Т₁ до Т₂ изменение энтропии можно выразить следующим образом:

;

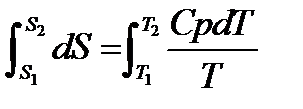
При помощи этого уравнения можно получить абсолютное значение энтропии вещества. Отметим существенное отличие абсолютных значений энтропии от значения других характеристических функций (∆U,∆H,∆G и ∆F), которые являются разностью двух состояний, а не абсолютными значениями.

При абсолютном нуле способность системы к рассеянию энергии иссекает; например, у совершенного

кристалла при абсолютном нуле все атомы находятся в регулярном однородном состояние без разупорядогенности. Они фиксированы в узлах кристаллической решетки и лишены возможности совершать какое — либо движение.

1. Первая строгая формулировка Планка:

Энтропия правильно образованного кристалла при Т=0К равна 0.

Подчеркнем, что речь идет о правильно образованном, бездефектном, совершенном кристалле. Большинство реальных кристаллов содержат примеси, имеют дефекты, а их энтропия даже при абсолютном нуле несколько больше нуля.

2. Можно показать, что энтропия равна:

По мере приближения к абсолютному нулю, когда Т→0 , теплоёмкость становиться бесконечно малой величиной и стремится к нулю. Тогда подынтегральное выражение в правой части управления (1) в результате деления двух бесконечно малых величин становится неопределённым, а само уравнение теряет смысл. Из этого в свою очередь вытекает следствие о недостижимости абсолютного нуля температуры. У каждого тела существует своя критическая температура , ниже которой охладить тело невозможно.

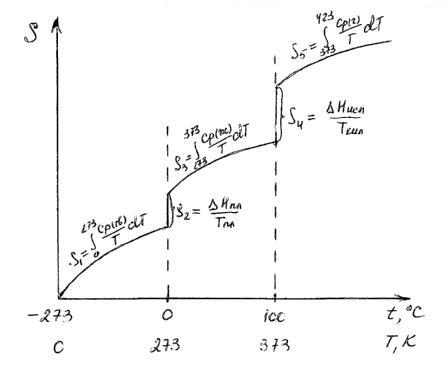
РАСЧЕТ АБСОЛЮТНОГО ЗНАЧЕНИЯ ЭНТРОПИИ

Третий закон термодинамики используется для вычисления абсолютных энтропий простых и сложных веществ. Абсолютной энтропией называется энтропия, отсчитанная относительно абсолютного нуля температуры S(0)=0.

Для расчетов необходимо учитывать следующие уравнения.

1.

2.

3.

Если вещество может находиться в различных агрегатных состояниях, то следует учитывать изменение энтропии при фазовых переходах. Тогда в общем случае для вещества в газообразном состоянии абсолютная энтропия будет складываться из следующих составляющих:

По этому уравнению можно вычислить абсолютные энтропии веществ в твердом, жидком и газообразном состояниях.

Пример. Рассчитать энтропию воды при t=150 0 C.

Энтропия воды при t=150 0 C(423К) равна:

;

;

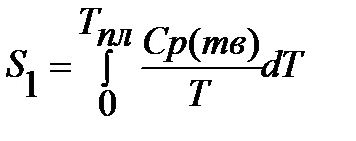
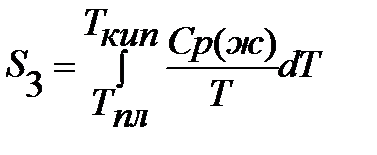
Третий закон термодинамики можно использовать для расчета химических равновесий.

РАСЧЕТ КОНСТАНТЫ РАВНОВЕСИЯ К_Р:

Теорема Нернста и её следствия

Вы будете перенаправлены на Автор24

Свой закон или теорему Нернст открыл эмпирическим путем. Эта теорема не может быть получена из первых двух начал термодинамики. В виду фундаментальности теорему Нернста часто зазывают третьим началом термодинамики. Современную ее формулировку представил Планк.

Теорема Нернста

Смысл теорему Нернста состоит из двух утверждений:

1. при приближении температуры к абсолютному нулю энтропия системы стремится к определенному конечному пределу;
2. все процессы при абсолютном нуле температур при переходе системы из равновесного состояния 1 в равновесное состояние 2 происходят без изменения энтропии.

Рассмотрим каждое из утверждений теоремы подробнее. Согласно термодинамическому определению энтропии (S) ее изменение равно:

где интеграл берется по произвольному пути, по которому система переходит из состояния (1) в состояние (2). В интеграле (1) в знаменателе дроби стоит температура (T) поэтому вопрос о сходимости интеграла при $T\to 0$ совсем не праздный. Первая часть теоремы Нернста как раз и говорит о том, что интеграл сходится.

Из второго утверждения входящего в теорему Нернста следует, что предел, к которому стремится интеграл (1) при $T\to 0$, не зависит от того, в каком конечном состоянии окажется система.

Исходя из вышесказанного, теорему Нернста можно сформулировать и следующим образом:

При приближении к нулю изменение энтропии системы стремится к конечному пределу, который не зависит от значений, которые принимают все параметры, которые характеризуют состояние системы.

Эта теорема относится только к состояниям термодинамического равновесия. Можно условиться считать энтропию системы при абсолютном нуле ($T=0K$) равной нулю, таким образом, избавиться от неоднозначности в определении энтропии. (Мы помним, что уравнение (1) в левой части включает изменение энтропии, а не ее саму.) В таком случае энтропию называют абсолютной. Третья формулировка теоремы Нернста может быть следующей:

Готовые работы на аналогичную тему

При $T\to 0$, абсолютная энтропия стремится к нулю ($S\to 0$) независимо от того, какие значения принимают другие параметры системы.

Абсолютный нуль температуры недостижим, поэтому о справедливости теоремы Нернста можно судить по поведению вещества вблизи абсолютного нуля.

Следствия из теоремы Нернста

Следствия из третьего начала термодинамики (теоремы Нернста):

1. Из первой части теоремы следует, что около $T=0K$ теплоемкости $C_p$ и $C_V$ стремятся к нулю у любых тел. Данное следствие показывает, что теплоемкости должны зависеть от температуры, тогда как классическая теория теплоемкости говорит об обратном. Следовательно, теорема Нернста не истолковывается в классических представлениях.
2. Прежде чем сформулировать следствие из второй части теоремы Нернста, запишем термодинамические соотношения, которые нам потребуются: \[<\left(\frac<\partial S><\partial p>\right)>_T=-<\left(\frac<\partial V><\partial T>\right)>_p,\ <\left(\frac<\partial S><\partial V>\right)>_T=-<\left(\frac<\partial p><\partial T>\right)>_V\left(2\right).\]

Из теоремы Нернста следует, что при T=0K левые части соотношений (2) обращаются в нуль. Значит, будут равны нулю и правые части, поэтому:

Это значит, что при $T\to 0$ для всех тел должны стремиться к нулю коэффициент теплового расширения и термический коэффициент давления. Однако из уравнения Клайперона следует, что оба коэффициента должны оставаться постоянными до T=0K. Следовательно, при низких температурах уравнение Клайперона не выполняется. Из формулы, в которую входит давление из (3) получается, что давление газа около абсолютного нуля практически не зависит от температуры и становится функцией плотности. В таком случае считают, что газ находится в состоянии вырождения. К вырожденным газам можно, например, отнести «газ» из свободных электронов в металлах даже при обычных температурах. К подобным газам классическая статистика не применима, необходимо использовать квантовую физику.

Для объяснения теоремы Нернста, также приходится прибегать к квантовой механике. Рассмотрим замкнутую систему. Под квантовым состоянием системы будем понимать состояние системы в целом. При $T\to 0\ K$ энергия системы минимальна. Количество допустимых квантовых состояний системы — один, либо если уровень энергии вырожден, это, какое то целое число, которое равно кратности вырождения. Тому же числу равен статистический вес состояния. Следовательно, энтропия в формуле Больцмана:

имеет конечное значение. Здесь Г — статистический вес системы (число микросостояний, с помощью которых реализуется макросостояние). Так, мы объяснили первую часть теоремы.

При изменении внешних параметров, например, p и V квантовое состояние и соответственно энергия системы изменяются. Кратные уровни могут расщепляться на простые, простые уровни могут объединяться. Однако общее количество простых уровней остается постоянным. Система, которая находится в термодинамическом равновесии, при T=0K занимает самый нижний энергетический уровень. Если при изменении внешних параметров кратность уровня не изменяется, то постоянен статистический вес, а следовательно, и энтропия, как и предполагается в теореме Нернста. Даже если кратность нулевого уровня изменится, то изменение энтропии будет крайне ничтожно.

Следствием теоремы Нернста является то, что тело невозможно охладить до температуры $T=0K$.

Задание: Покажите, что при $T\to 0\ K$ $C_p$ и $C_V$ стремятся к нулю.

В качестве основы для решения используем известное уравнение:

\[\delta Q=CdT\ \left(1.1\right),\]

где в качестве $C$ — может быть и $C_V$ и $C_p$ в зависимости от избираемого процесса, что ни как не отражается на форме уравнения (1.1), поэтому доказательство приведем обозначая теплоёмкость просто $C$.

Из (1.1) выразим теплоемкость, запишем:

Кроме того, мы знаем, что:

\[\delta Q=TdS\ \left(1.3\right).\]

Из уравнений (1.2) и (1.3) получаем:

Пусть в выражении (1.2) $T\to 0$ тогда $lnT\to -\infty $, $S$ стремится к определенному пределу (по теореме Нернста).

Следовательно, мы доказали, что при $T=0K$ $C_V=0$ и $C_p=0$.

Задание: Какой вывод можно сделать о поведении диэлектрической проницаемости вблизи $T=0K$?

Электрический момент единицы объема равен:

\[l=\left(\varepsilon -1\right)\frac<4\pi >\ \left(2.1\right),\]

где $\varepsilon $ — диэлектрическая проницаемость среды, $E$ — напряженность электрического поля.

При $T\to 0$ по теореме Нернста имеем:

С другой стороны можно записать, что:

Учитывая (2.1), (2.3) и (2.4), мы можем записать, что:

В том случае, если мы считаем, что $\varepsilon $ от напряженности электрического поля не зависит, то получаем, что:

Ответ: Мы получили, что около абсолютного нуля диэлектрической проницаемости среды стремится к нулю.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 27 11 2021