Термическое и калорическое уравнения состояния системы

Термическое и калорическое уравнения состояния. Термическое уравнение состояние идеального газа

Второй постулат ТД приводит к существованию функциональных соотношений, называемых уравнения состояния, устанавливающих связь между внешними параметрами, температурой и каким-либо внутренним параметром состояния макросистемы. Т.е. параметры системы не могут принимать произвольное значение. Для любой системы они связаны некоторым функциональным соотношением.

Если этим внутренним параметром является внутренняя энергия 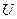, то уравнение называется калорическим уравнением состояния.

Если внутренним параметром является какая-либо обобщенная сила, то уравнение называется термическим уравнение состояния.

Общее число термических и калорического уравнений состояния системы равно числу ее степеней свободы, т.е. числу независимых параметров, характеризующих состояние системы. Если все эти уравнения состояния известны, то с помощью начал термодинамики можно определить все термодинамические свойства системы.

Вывести сами уравнения состояния на основе начал ТД нельзя. Для каждой конкретной системы они определяются эмпирически, т.е. берутся из опыта, или находятся методами статистической физики. Так что в рамках ТД они считаются заданными при определении системы.

До сих пор не существует удовлетворительной общей теории уравнений состояния, кроме случаев особых простых систем: идеального газа и совершенных кристаллов. Для жидкостей и твердых тел соотношения между параметрами состояния до сих пор получают эмпирически.

Ограничимся рассмотрением простых систем, систем с постоянным числом частиц, состояние которых определяется только одним внешним параметром и температурой.

Термическое уравнение состояния такой системы, записанное в общем виде:

.

Калорическое уравнение состояния, записанное в общем виде:

.

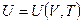
для идеального газа уравнение состояния (термическое) — это уравнение
Менделеева-Клапейрона ;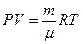

для модели реального газа уравнение состояния — это уравнение Ван-дер-Ваальса

— для одного моля вещества.

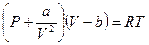
Если известны два параметра, то третий находится из уравнения состояния

.

Например: , , .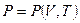

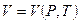
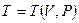
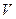
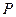
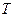
Уравнение состояния изображается в условном пространстве , , поверхностью состояний. Каждой точке такой поверхности соответствует определенное состояние данной системы, и наоборот, точке не лежащей на поверхности не соответствует никакое состояние этой системы.

Калорическое и термическое уравнения состояния системы

Уравнение (П.4.1) является универсальным, и, в этой связи, применимым для всех типов макроскопических систем. Однако, даже для простейшего случая термодинамической системы (идеальный газ)

,

(П.4.2)

это уравнение является неразрешимым, поскольку содержит пять переменных 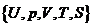. Следовательно, его практическое применение для конкретной термодинамической системы сопряжено с необходимостью дополнения к этому уравнению ряд дополнительных соотношений, характеризующих специфику рассматриваемой системы.

Для изыскания этих соотношений следует обратить внимание на тот факт, что равновесные внутренние параметры системы являются функциями внешних параметров и температуры системы, что приводит к существованию термических и калорических уравнений состояния системы. Эти дополнительные уравнения должны связывать температуру T и внешние параметры a_i с каким либо внутренним параметром b_k термодинамической системы:

(П.4.3)

Если в качестве внутреннего параметра b_k выступает непосредственно внутренняя энергия системы U (т.е.: b_k = U), то получается калорическое уравнение состояния системы:

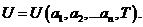(П.4.4)

Своим названием калорическое уравнение состояния обязано тому обстоятельству, что с его помощью можно находить теплофизические характеристики материалов, например, теплоемкость веществ.

Если же внутренним параметром b_k является сопряженная внешнему параметру a_i обобщенная сила A_i (т.е. b_k = A_i), то получается термическое уравнение состояния системы:

где: i = 1, 2,…n.

(П.4.5)

Своим названием термическое уравнение состояния обязано тому обстоятельству, что с его помощью можно находить температуру системы.

Общее число термических и калорических уравнений состояния системы равно числу ее степеней свободы, т.е. числу независимых параметров однозначно характеризующих состояние системы. Согласно постулатам равновесной термодинамики калорическое и каждое из термических уравнений состояния системы не являются независимыми (связаны дифференциальным уравнением в частных производных).

Если калорическое и все термические уравнения состояния системы известны, то далее, с помощью теоретического аппарата термодинамики, можно определить все термодинамические свойства системы. Важно отметить, что вывести (теоретическим путем) упомянутые выше уравнения состояния системы с помощью методов термодинамики не представляется возможным. Эти уравнения устанавливаются либо опытным путем, либо – с помощью теоретического аппарата статистической физики.

Методологические принципы практического использования калорического и термических уравнений состояния удобно проиллюстрировать на примере анализа простейшей термодинамической системы – «идеальный газ», для которой эти уравнения имеют соответственно вид (обратить внимание на то, что система имеет две степени свободы):

(термическое уравнение).	(П.4.6.а)
(калорическое уравнение).	(П.4.6.б)

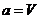
Если принять в качестве обобщенной силы 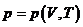(давление газа) и сопряженную этой силе обобщенную координату (объем газа), то уравнения состояния приобретают вид:

(термическое уравнение).	(П.4.7.а)
(калорическое уравнение).	(П.4.7.б)

Для идеального газа термическим уравнением состояния является известное уравнение Клайперона-Менделеева (определено эмпирическим путем!):

(термическое уравнение).

(П.4.8)

Обратить внимание на то обстоятельство, что наличие выражения (П.4.8) уменьшает число степеней свободы термодинамической системы на единицу.

Используя закон Джоуля о независимости внутренней энергии идеального газа от его объема при постоянной температуре (т.е. исключается из рассмотрения потенциальная энергия взаимодействия атомов газа между собой: ), для калорического уравнения имеем:

,

(П.4.9)

где — теплоемкость газа при постоянном объеме.

Согласно опытным данным, теплоемкость не зависит от температуры газа (элемент идеализации в постановке задачи), поэтому, в результате интегрирования выражения (П.4.9), для калорического уравнения имеем:

,

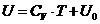(П.4.10)

где — постоянная интегрирования, зависящая только от типа рассматриваемого газа.

Рассмотренный случай («идеальный газ») является самым простым в практике анализа термодинамических систем. Уже для случая «реальных газов» (не говоря уж о конденсированных средах) трудности нахождения уравнений состояния системы неизмеримо возрастают. Именно это обстоятельство является сдерживающим фактором на пути широкого использования (внедрения) теоретических подходов равновесной термодинамики в производственно-техническую практику, связанную с созданием устройств электронной техники.

Не нашли, что искали? Воспользуйтесь поиском:

Термическое и калорическое уравнения состояния системы

Из основных положений статистической механики следует, что термодинамические свойства классической системы, состоящей из N одинаковых частиц и занимающей объем V при температуре T, полностью определяются канонической статистической суммой (статистическим интегралом):

Z(T,V,N) = 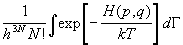, (2.1)

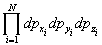
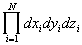
где H(p,q) — классическая функция Гамильтона системы, dГ = d 3N p d 3N q — элемент фазового объема (d 3N p =, d 3N q =), h — постоянная Планка, k — постоянная Больцмана. Интеграл в (2.1) имеет кратность 6N и размерность (координатаґ импульс) 3N . Сама статистическая сумма безразмерна.

Статистическая сумма содержит в себе всю термодинамическую информацию о системе. Если удалось теоретически рассчитать статистическую сумму (как это сделать — отдельный вопрос), то можно определить все термодинамические функции и вывести термическое и калорическое уравнения состояния. Так, свободная энергия Гельмгольца связана со статистической суммой соотношением:

Энтропия и давление системы связаны с производными статистической суммы по температуре и объему, соответственно:

, (2.3)

. (2.4)

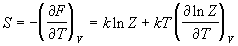
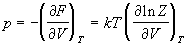
Последнее соотношение дает давление как функцию температуры и объема, т.е. термическое уравнение состояния. Калорическое уравнение состояния, т.е. зависимость внутренней энергии от температуры и объема дается соотношением:

. (2.5)

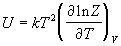
Таким образом, основная задача классической статистической термодинамики состоит в расчете статистической суммы (2.1).

Формулы (2.2) – (2.5), выражающие связь между термодинамикой и статистической механикой, справедливы для любых термодинамических систем. Формула (2.1) справедлива только для классических систем, в которых квантовые эффекты несущественны, в частности для систем, состоящих из частиц, не имеющих внутренней структуры. Многие такие системы (например, газы и жидкости) описываются гамильтонианом вида

, (2.6)

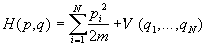
где m — масса частиц, V — потенциальная энергия их взаимодействия друг с другом. В гамильтониане (2.6) координаты и импульсы разделены, поэтому интегрирование по ним можно провести независимо. Подставляя (2.6) в (2.1) и вычисляя интегралы по N импульсам

,

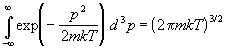
получаем статистическую сумму в виде

. (2.7)

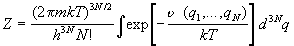
Интеграл по координатам в формуле (2.7) называют конфигурационным интегралом:

. (2.8)

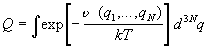
Именно он определяет зависимость статистической суммы от объема и содержит в себе описание всех отклонений системы от идеального поведения. Давление системы определяется только конфигурационным интегралом:

. (2.9)

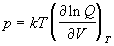
2.2. Статистическая термодинамика идеального одноатомного газа

Для идеального газа потенциал взаимодействия частиц равен нулю. Кроме того, в этой модели частицы не имеют собственного объема, поэтому интегрирование по координатам проводится по всему объему системы и конфигурационный интеграл равен

.

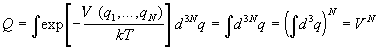
Статистическая сумма имеет вид:

. (2.10)

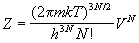
Все термодинамические функции выражаются через логарифм статистической суммы:

. (2.11)

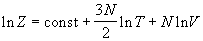
Подставляя (2.11) в (2.4), находим термическое уравнение состояния идеального одноатомного газа (зависимость давления от температуры и объема):

,

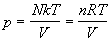
где n = N / N_A — число молей, R = kЧ N_A — универсальная газовая постоянная. Калорическое уравнение состояния (зависимость внутренней энергии от температуры и объема) получается при подстановке (2.11) в (2.5):

.

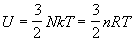
Наконец, из (2.10) и (2.3) можно получить уравнение Закура-Тетроде для энтропии одного моля одноатомного идеального газа:

,

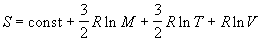
где M = mЧ N_A — молярная масса газа. Значение постоянной в этом уравнении зависит от размерностей величин, стоящих под знаком логарифма [4, с. 210].

Таким образом, на примере идеального газа мы реализовали схему, демонстрирующую связь микроскопических свойств (гамильтониана) системы с ее макроскопическими (т.е., термодинамическими) свойствами:

(2.2) – (2.5)

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору