Тест иррациональные уравнения и их системы

Тест с ответами: “Иррациональные уравнения”

1. Найдите корень уравнения:

а) 38 +
б) 16
в) 22

2. Найдите корень уравнения: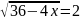

а) 12
б) 8 +
в) 14

3. Найдите корень уравнения: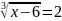

а) 12
б) 18
в) 14 +

4. Найдите корень уравнения: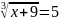

а) 116 +
б) 88
в) 94

5. Решите уравнение: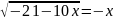

Если уравнение имеет больше одного корня, в ответе запишите больший из корней:
а) 3
б) 5
в) -3 +

6. Решите уравнение: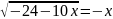

Если уравнение имеет больше одного корня, в ответе запишите меньший из корней:
а) 6
б) -6 +
в) -12

7. Решите уравнение:

Если уравнение имеет больше одного корня, в ответе запишите меньший из корней:
а) -15
б) 5
в) -5 +

8. Решите уравнение: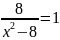

Если уравнение имеет больше одного корня, в ответе запишите больший из корней.
а) 4 +
б) -4
в) 8

9. Решите уравнение: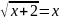

Если уравнение имеет больше одного корня, в ответе запишите меньший из корней:
а) 4
б) -2
в) 2 +

10. Иррациональными называются уравнения, в которых переменная содержится под знаком корня, так ли это:
а) да +
б) нет
в) отчасти

11. Иррациональное уравнение, как правило, сводится к равносильной системе, содержащей уравнения и неравенства, так ли это:
а) да +
б) нет
в) зависит от условия задачи

12. Иррациональные уравнения могут быть также решены путем возведения обеих частей уравнения в натуральную степень, так ли это:
а) да +
б) нет
в) зависит от условия задачи

13. При возведении уравнения в степень могут появиться посторонние корни. Поэтому необходимой частью решения иррационального уравнения является проверка, так ли это:
а) да +
б) нет
в) зависит от условия задачи

14. Один из методов решения иррациональных уравнений:
а) метод введения старых переменных
б) метод введения новых переменных
в) метод введения новых переменных +

15. Один из методов решения иррациональных уравнений:
а) переход к равносильной системе (в этом случае проверка не нужна) +
б) метод введения старых переменных
в) метод возведения обеих частей уравнения в разные степени

16. Один из методов решения иррациональных уравнений:
а) метод возведения обеих частей уравнения в разные степени
б) метод возведения обеих частей уравнения в одну и ту же степень +
в) метод введения новых переменных

17. Правильно решите: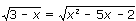

а) 1
б) 4
в) -1 +

18. Правильно решите: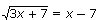

а) -14
б) 14 +
в) 28

19. Правильно решите: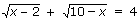

а) 12
б) -6
в) 6 +

20. Правильно решите: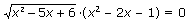

а) 4
б) +
в) 5

21. Правильно решите: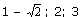

а) 7 +
б) -7
в) 14

22. Алгебраическое уравнение называется иррациональным, если оно содержит переменные под знаком корня или в основе степени с дробным показателем, так ли это:
а) нет
б) да +
в) отчасти

23. Какое из перечисленных чисел является иррациональным:
а) 1/2
б) 0
в) √5 +

24. Как называется уравнение, содержащее неизвестное в определенной дробной степени:
а) рациональное
б) иррациональное +
в) дробное

25. Уравнение называется алгебраическим, если обе его части – … выражения:
а) математические
б) равнозначные
в) алгебраические +

26. Область допустимых значений (сокращённо ОДЗ) уравнения есть множество значений переменной, при которых обе части данного уравнения имеют смысл, так ли это:
а) нет
б) да +
в) отчасти

27. В большинстве ситуаций специально искать ОДЗ:
а) не нужно искать +
б) нужно искать
в) по желанию

28. Основной метод решения иррациональных уравнений:
а) метод утроения радикала
б) метод удвоения радикала
в) метод уединение радикала +

29. При решении иррационального уравнения с радикалом нечетной степени возведение в нечетную степень правой и левой части уравнения всегда приводит к равносильному уравнению и потеря корней или их приобретения происходить не может, так ли это:
а) да +
б) нет
в) отчасти

30. Иррациональные числа невозможно представить в виде дроби, так ли это:
а) нет
б) да
в) отчасти

Зачёт по теме «Решение иррациональных уравнений»

Зачётные задания по теме «Решение иррациональных уравнений» предназначены для проверки уровня знаний, умений и навыков учащихся 10 или 11 класса по данной теме и могут помочь выпускникам при подготовке к ЕГЭ. При решении заданий данного зачётного задания необходимо хорошо знать и уметь применять на практике основные алгоритмы решения иррациональных уравнений. В тесте представлены два варианта, в каждом из которых четырнадцать уравнений, и ответы к ним.

Устная (теоретическая) часть зачёта

1. Какое уравнение называют иррациональным?

2. Какое условие накладывается на подкоренное выражение корня чётной степени?

3. Какое условие накладывается на ту часть иррационального уравнения, которая не находится под корнем?

4. Как называется числовое значение неизвестного, удовлетворяющее уравнению с одним неизвестным?

5. Какие алгоритмы решения иррационального уравнения вы знаете?

Тест иррациональные уравнения и их системы

Произведение корней уравнения $$\sqrt[3]<\sqrt<1+x^<2>>-10>=-2$$ равно:

Если уравнение имеет вид $$\sqrt[3]=\varphi (x)$$ , то возведя обе части уравнения в куб, получим равносильное ему уравнение $$f(x)=\varphi^ <3>(x)$$ .

ОДЗ: так как 0″>$$1+x^<2>>0$$ , то $$x\in R$$ .
Тогда:

1. Возводить уравнение в четную степень можно только при условии, что обе его части не отрицательны.
2. Возводить уравнение в нечетную степень можно и при отрицательной правой части.

Произведение корней (или корень, если он единственный) уравнения $$\left (8-x \right )\sqrt<16-x^2>=0$$ равно:

Если уравнение имеет вид $$f(x)\cdot g(x)=0$$ , то на ОДЗ оно равносильно совокупности уравнений: $$f(x)=0$$ или $$g(x)=0$$ .

1. Выражение, записанное под знаком корня четной степени, не должно быть отрицательным.
2. Совокупность уравнений мы решали на ОДЗ.

Произведение всех корней уравнения $$\sqrt<2x^2-x-15>=4x^2-2x-45$$ равно:

1. Значение корня четной степени не может быть отрицательным.
2. Применяя теорему Виета, необходимо находить дискриминант уравнения, потому что, если он отрицательный, то уравнение вовсе не имеет корней.

1. Иррациональным называют уравнение, содержащее переменную под знаком радикала.
2. Область допустимых значений иррационального уравнения состоит из тех значений переменной, при которых неотрицательны все выражения, стоящие под знаками радикалов четной степени.
3. Дробным называют уравнение, содержащее переменную в знаменателе дроби.
4. Область допустимых значений дробного уравнения не содержит тех значений переменной, которые обращают в нуль знаменатель дроби.

Так как уравнение дробно-иррациональное, то оно лишено смысла в случае, когда:

1) $$x-2\leq 0$$, откуда $$x\leq 2$$;

Область допустимых значений выражения $$\sqrt[3]<2x+1>$$ – множество всех действительных чисел.

Среднее арифметическое корней (или корень, если он единственный) уравнения $$\sqrt<2-x>+\sqrt<3-x>=1$$ равно:

Если уравнение имеет вид $$\sqrt+\sqrt=\varphi (x)$$ , то
ОДЗ: $$\left\ <\begin \geq 0, & & \\ g(x)\geq 0, & & \\ \varphi (x) \geq 0.& & \end\right.$$
Возведем обе части уравнения в квадрат:
$$\left (\sqrt+\sqrt \right )^<2>=\left (\varphi (x) \right )^<2>.$$
«Уединим» радикал, приведем подобные слагаемые и снова возведем обе части полученного уравнения в квадрат при условии, что обе части и этого уравнения не отрицательные.