Тест по дифференциальным уравнениям первого порядка
Решение уравнения $$y’x=2y$$ при условии, что $$x_0=-2$$ , а $$y_0=10$$ , имеет вид:
Запишем уравнение в виде:
$$y=Cx^2$$ – общее решение уравнения.
Подставляя в общее решение значения $$x_0=-2$$ и $$y_0=10$$ найдем произвольную постоянную:
Подставляя значение $$C=2,5$$ в общее решение, найдем частное решение:
Различайте общее решение $$y=\phi (x;C)$$ и частное решение $$y=\phi (x)$$ дифференциального уравнения первого порядка.
Решением дифференциального уравнения $$y’-3x(x^2-1)=\frac
Полагая $$y=uv$$ , $$y’=u’v+uv’$$ , получим:
Сгруппируем слагаемые, содержащие множитель $$u$$ , и вынесем его из скобок:
Если положим $$v’-\frac
Решим уравнение $$(1)$$ :
Подставим полученное значение $$v=(x^2-1)^<0,5>$$ в уравнение $$(2)$$ и решим его:
Так как $$y=uv$$ , то получим:
Решая первое уравнение системы всегда полагаем $$C=0$$ .
Общее решение уравнения $$5dy=(2x+1)dx$$ имеет вид:
Дифференциальное уравнение с разделенными переменными имеет вид:
Чтобы решить это уравнение, необходимо проинтегрировать его обе части.
$$\int 5dy=\int (2x+5)dx$$ ,
Решение уравнения $$y’+y=e^x$$ имеет вид:
Дифференциальное линейное уравнение первого порядка имеет вид:
Чтобы решить это уравнение, необходимо применить подстановку:
Полагая $$y=uv$$ , $$y’=u’v+uv’$$ , получим:
Сгруппируем слагаемые, содержащие множитель $$u$$ , и вынесем его из скобок:
Если положим $$v’+v=0$$ , то получим: $$u’v=e^x$$ .
Запишем систему уравнений: $$\begin
Решим первое уравнение системы:
Подставим полученное значение $$v=e^<-x>$$ во второе уравнение системы и решим его:
Так как $$y=uv$$ , то получим:
$$y’=\frac
Решая первое уравнение системы всегда полагаем $$C=0$$ .
Тест с ответами: “Дифференциальные уравнения”
1. Уравнение, которое помимо функции содержит её производные:
а) дифференциальное уравнение +
б) иррациональное уравнение
в) тригонометрическое уравнение
2. Решите задачу Коши 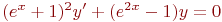
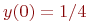
а) 1
б) 0 +
в) 10
3. Порядок входящих в уравнение производных:
а) ограничен
б) может быть различен +
в) зависит от условия задачи
4. Дифференциальное уравнение порядка выше первого можно преобразовать в систему уравнений первого порядка, в которой число уравнений равно порядку исходного дифференциального уравнения, так ли это:
а) нет
б) да +
в) отчасти
5. Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или отсутствовать вовсе, кроме хотя бы одной производной, так ли это:
а) нет
б) да +
в) отчасти
6. Важнейшим вопросом для дифференциальных уравнений является существование и единственность их решения, так ли это:
а) нет
б) да +
в) отчасти
7. При решении дифференциальных уравнений ищется:
а) функция (семейство функций) +
б) число (несколько чисел)
в) оба варианта верны
8. После определения вида указанных постоянных и неопределённых функций решения становятся:
а) частными +
б) общими
в) практическими
9. Дифференциальное уравнение порядка выше первого можно преобразовать в систему уравнений первого порядка, в которой число уравнений равно порядку исходного дифференциального уравнения, так ли это:
а) нет
б) да +
в) отчасти
10. Решения дифференциальных уравнений подразделяются на:
а) теоретические
б) общие +
в) практические
11. Что является порядком дифференциального уравнения:
а) наивысший порядок входящих в него производных +
б) низший порядок входящих в него производных
в) средний порядок входящих в него производных
12. Решения дифференциальных уравнений подразделяются на:
а) дробные
б) частные +
в) цельные
13. Если дифференциальное уравнение является многочленом относительно старшей производной, то степень этого многочлена называется:
а) степенью дифференциального уравнения +
б) порядком дифференциального уравнения
в) объектом дифференциального уравнения
14. Решите задачу Коши , . В ответе укажите значение её решения при :
а) 5
б) 25
в) -25 +
15. Дифференциальное уравнение для функции от одной переменной:
а) обыкновенное дифференциальное уравнение +
б) простейшие дифференциальные уравнения первого порядка
в) дифференциальные уравнения в частных производных
16. Решите задачу Коши , . В ответе укажите значение её решения при 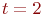
а) 3
б) 2 +
в) 1
17. Одно из простейших применений дифференциальных уравнений — решение нетривиальной задачи нахождения траектории тела по известным проекциям ускорения, так ли это:
а) да +
б) нет
в) лишь отчасти
18. Найдите абсциссу точки пересечения прямой 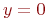
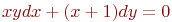
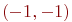
а) 2
б) -1 +
в) 0
19. Класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию:
а) дифференциальные уравнения в частных производных
б) обыкновенное дифференциальное уравнение
в) простейшие дифференциальные уравнения первого порядка +
20. Найдите решение уравнения 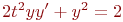
а) 4
б) -2
в) 2
21. Дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные:
а) дифференциальные уравнения в частных производных +
б) обыкновенное дифференциальное уравнение
в) простейшие дифференциальные уравнения первого порядка
22. Найдите решение уравнения 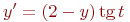
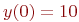
а) -4
б) 6 +
в) 4
23. Составьте дифференциальное уравнение семейства кривых :
а)
б)
в) +
24. Найдите решение уравнения 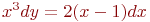
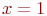
а) 1
б) -1 +
в) 10
25. Составьте дифференциальное уравнение семейства кривых :
а) 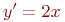
б)
в) +
26. Найдите решение уравнения 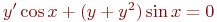
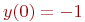
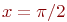
а) 1
б) -1 +
в) -10
27. Составьте дифференциальное уравнение семейства кривых 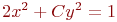
а) +
б) 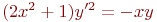
в)
28. Найдите решение уравнения , удовлетворяющее начальному условию . В ответе укажите его значение при :
а) 31
б) 51
в) 101 +
29. Найдите решение уравнения , удовлетворяющее начальному условию. В ответе укажите его значение при :
а) 30 +
б) 10
в) 20
30. Найдите решение уравнения 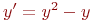
а) 2
б) 1 +
в) 3
Тест по теме «Дифференциальные уравнения первого порядка»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
по теме «Дифференциальные уравнения первого порядка»
1. Установить соответствие между приведенными дифференциальными уравнениями первого порядка и их типами:
1) ; а) с разделяющимися переменными;
2) ; б) в полных дифференциалах;
4) . г) однородное.
2. Выяснить при каких целых значениях параметров и функция является решением уравнения .
Найти интегральную кривую уравнения , проходящую через точку (2;0).
Пусть — решение уравнения , удовлетворяющее начальному условию . Найти (с точностью до целых) .
Пусть — интегральная кривая уравнения , проходящая через точку . Найти .
Пусть — решение уравнения , удовлетворяющее начальному условию . Найти .
Найти уравнение касательной в точке (1;2) к интегральной кривой уравнения .
Пусть — решение уравнения , удовлетворяющее условию =2. Найти (с точностью до 0,1).
Найти решение уравнения , удовлетворяющее условию . В ответе дать значение .
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 939 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 686 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 313 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 589 668 материалов в базе
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 27.05.2018
- 612
- 5
- 27.05.2018
- 199
- 0
- 27.05.2018
- 446
- 0
- 27.05.2018
- 313
- 0
- 27.05.2018
- 453
- 1
- 27.05.2018
- 528
- 12
- 27.05.2018
- 1426
- 1
- 27.05.2018
- 561
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 27.05.2018 1859
- DOCX 54.4 кбайт
- 30 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Лещенко Марина Юрьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 7 лет и 3 месяца
- Подписчики: 10
- Всего просмотров: 62093
- Всего материалов: 36
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей
Время чтения: 1 минута
Каждый второй ребенок в школе подвергался психической агрессии
Время чтения: 3 минуты
Минпросвещения подключит студотряды к обновлению школьной инфраструктуры
Время чтения: 1 минута
В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных
Время чтения: 1 минута
Университет им. Герцена и РАО создадут портрет современного школьника
Время чтения: 2 минуты
Инфоурок стал резидентом Сколково
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Только 23 февраля!
Получите новую
специальность
по низкой цене
Цена от 1220 740 руб. Промокод на скидку Промокод скопирован в буфер обмена ПП2302 Выбрать курс Все курсы профессиональной переподготовки
http://liketest.ru/algebra/test-s-otvetami-differenczialnye-uravneniya.html
http://infourok.ru/test-po-teme-differencialnie-uravneniya-pervogo-poryadka-3066196.html



