3. Частотные характеристики звеньев и систем автоматического управления. ч. 3.2 Простейшие типовые звенья
Лекции по курсу «Управление Техническими Системами» читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки» факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность!
Данные лекции готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.
Тема сегодняшней статьи:
3.2. Типовые звенья систем автоматического управления (регулирования). Классификация типовых звеньев. Простейшие типовые звенья.
Хочешь вкусить плодов познания? — Грызи гранит науки!
Понятие “типовые звенья” в теории управления техническими системами, в основном, связано с описанием САУ (САР) в переменных “вход – выход”, т.е. описание систем в передаточных функциях. Любую линейную САУ (САР) или линеаризованную САР можно структурно расчленить на простейшие элементы (звенья), соединенные между собой соответствующими последовательными, параллельными связями, местными и локальными обратными связями, сумматорами, сравнивающими устройствами и т.д.
Достигнуто общепринятое соглашение, что наиболее удобно расчленять структурную схему САР на звенья 1-го и 2-го порядков. Принято называть такие простейшие звенья типовыми.
С другой стороны, реальная линеаризованная (линейная) система состоит из набора отдельных узлов и агрегатов, соединенных соответствующими связями, причем порядок уравнений динамики вышеуказанных узлов и агрегатов может быть и выше второго. В этом случае звенья (узлы и агрегаты) САР можно классифицировать по их свойствам.
Различают 3 типа звеньев:
Существуют также особые звенья, которые будут рассмотрены позднее.
Учитывая, что передаточная функция линейного (линеаризованного) звена может быть записана как:
где: и
— полиномы по степеням s, причем коэффициенты при низшей степени s в полиномах
,
равны 1, классификацию на типы звеньев можно объяснить видом полиномов
или (что эквивалентно) видом коэффициентов в соответствующих уравнениях динамики звена.
Подробнее о передаточной функции см. здесь.
Позиционным звеном считают звено, в котором полиномы N(s) и L(s) содержат свободные члены (равные 1). Например:
или в уравнении динамики (x(t) – входной сигнал, y(t) – выходной):
Из типовых звеньев (1-го и 2-го порядка) к позиционным звеньям относятся: идеальное усилительное звено, апериодические звенья 1-го и 2-го порядка, колебательное звено и форсирующее звено.
Дифференцирующим звеном считается звено, в котором полином L(s) содержит свободный член (равный 1), а полином N(s) не содержит свободного члена ().
Например:
или в уравнении динамики:
Из типовых звеньев к дифференцирующим звеньям относятся идеальное дифференцирующее звено, инерционно-дифференцирующее звено.
Интегрирующим звеном считается звено, в котором полином N(s) содержит свободный член (), а полином L(s), не содержит свободного члена (
). Например:
или в уравнении динамики:
Из типовых звеньев к интегрирующим звеньям относятся идеальное интегрирующее звено, инерционно–интегрирующее звено.
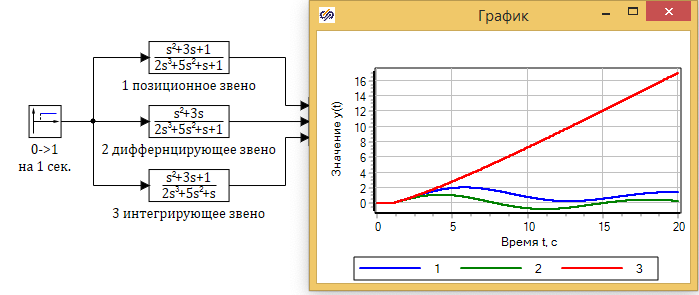
Пример переходного процесса при единичном ступенчатом воздействии на три разных звена, приведенных выше:
3.2.1. Идеальное усилительное звено
Уравнение динамики каждого звена имеет вид: , т.е. уравнение не является дифференциальным, следовательно, данное звено является безынерционным.
Переходя к изображениям , получаем:
– уравнение динамики звена в изображениях.
Передаточная функция идеального усилительного звена:
АФЧХ не зависит от ω, поскольку:
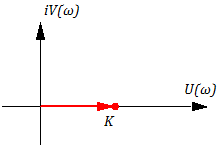
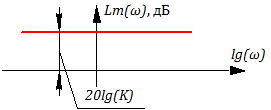
Рисунок 3.2.1 АФЧХ идеального усилительного звена
Годограф АФЧХ “вырождается” в точку: U(ω) =K; V(ω) =0;
A(ω) ≡modW(iω) =│W(iω)│=K =>
Lm(ω)=20lgA(ω) =20lgK; =>
φ(ω) = const = 0 т.е. фазового сдвига нет. Следовательно, данное звено является безынерционным, чисто усилительным звеном.
Рисунок 3.2.4 ЛАХ идеального усилительного звена
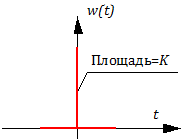
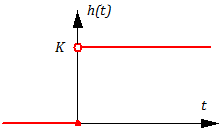
Найдем весовую w(t) и переходную h(t) функции звена (подробнее см. здесь).
Весовая функция:
3.2.2. Идеальное дифференцирующее звено
Уравнение динамики звена имеет вид:
где: – постоянная времени.
Переходя к изображениям:
Уравнение динамики звена в изображениях:
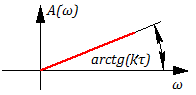
Передаточная функция идеального дифференцирующего звена:
Графики годографа АФЧХ, A(ω) и φ(ω) имеют вид:
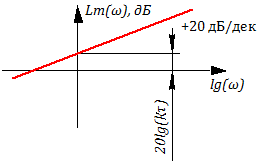
Логарифмическая амплитудная характеристика ЛАХ::
Из рисунка 3.2.9 видно, что данное звено обеспечивает опережение по фазе на /2 (при любой частоте входного сигнала).
Чем выше частота единичного гармонического сигнала на входе в звено, тем выше амплитуда выходного сигнала в установившемся режиме.
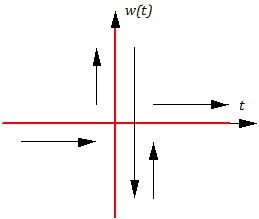
Найдем весовую функцию звена:
Учитывая, что δ(t) имеет вид как на рис.3.2.11 (зависимость показана утрированно), а весовая функция пропорциональна производной от δ(t):
Найдем переходную функцию звена:
Иногда идеальное дифференцирующее звено представляется в виде или
. В последнем варианте коэффициент К имеет смысл постоянной времени.
3.2.3. Идеальное интегрирующее звено
Уравнение динамики такого звена имеет вид:
или в изображениях:
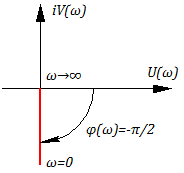
Передаточная функция идеального интегрирующего звена:
Умножая числитель и знаменатель на i, получаем:
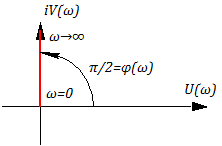
Годограф АФЧХ имеет вид:
Данное звено всегда дает отставание по фазе на угол .
Найдем весовую функцию звена:
Найдем переходную функцию звена:
Примерами устройств, близких к идеальному усилительному звену, можно считать: широкополосный электронный усилитель (приближенно), механический редуктор без учета инерционности и нелинейных эффектов, жесткую механическую муфту и т.д.
Примером идеального дифференцирующего звена можно считать тахогенератор:
где u(t) – напряжение на клеммах тахогенератора, φ(t) – угол поворота якоря (ротора) тахогенератора.
Примером идеального интегрирующего звена можно считать большинство электродвигателей (без учета инерционности якоря), где входным воздействием считать напряжение в обмотке возбудителя (двигателем постоянного тока), а выходным воздействием – угол поворота выходного вала.
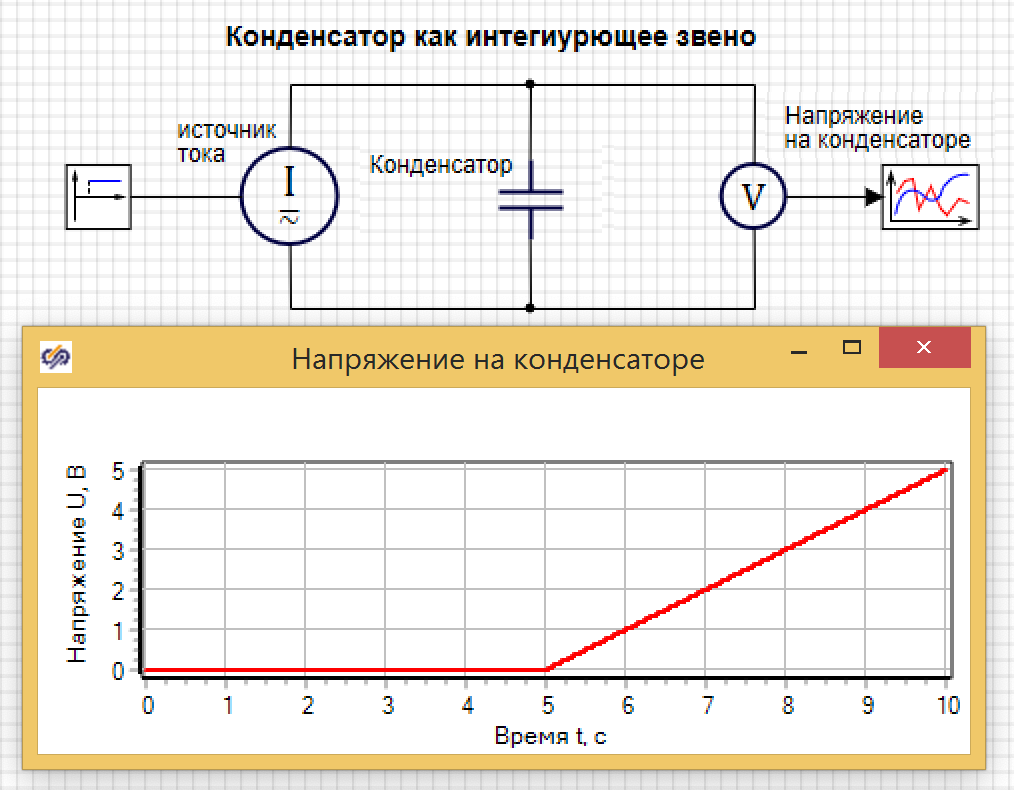
Пример интегрирующего и дифференцирующего звена на основе конденсатора
Один и тот же технический элемент, с точки зрения теории автоматического управления, может выступать как в качестве интегрирующего, так и в качестве дифференцирующего звена.
В качестве примера интегрирующего звена можно рассмотреть конденсатор, где входным воздействием является ток, а выходным результатом является напряжение на клеммах конденсатора. Действительно, при малом токе и большой емкости конденсатора, в случае ступенчатого изменения тока с 0, мы получаем график напряжения, совпадающий по форме с переходной функцией интегрирующего звена. На рисунке 3.2.20 представлена такая модель, где ток ступенькой меняется на пятой секунде расчета.
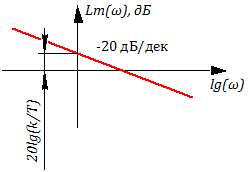
Если построить с помощью гармонического анализатора ЛАХ и ФЧХ, мы увидим, что угол наклона ЛАХ составляет -20 dB/dec, а угол сдвига фазы равен — или -90 градусов на графике (см. рис. 3.2.21).
Тот же самый конденсатор, при определенных параметрах сети, может выступать в качестве идеального дифференцирующего звена, если в качестве входного воздействия подавать напряжение, а в качестве результирующей величины использовать ток в цепи.
Электрическая схема использования конденсатора в качестве дифференцирующего звена с гармоническим анализатором приведена на рисунке 3.2.22. На графиках гармонического анализатора видно, что угол наклона ЛАХ составляет 20 dB/dec, а угол сдвига фазы равен или 90 градусов на графике.
Примеры моделей, использованные в данной лекции, можно взять в этом архиве.
Типовые динамические звенья
Типовые звенья САУ и их характеристики
Типовые динамические звенья
Типовым динамическим звеном САУ является составная часть системы, которая описывается дифференциальным уравнением не выше второго порядка. Звено, как правило, имеет один вход и один выход. По динамическим свойствам типовые звенья делятся на следующие разновидности: позиционные, дифференцирующие и интегрирующие.
Позиционными звеньями являются такие звенья, у которых в установившемся режиме наблюдается линейная зависимость между входными и выходными сигналами. При постоянном уровне входного сигнала сигнал на выходе также стремится к постоянному значению.
Дифференцирующими являются такие звенья, у которых в установившемся режиме выходной сигнал пропорционален производной по времени от входного сигнала.
Интегрирующими являются такие звенья, у которых выходной сигнал пропорционален интегралу по времени от входного сигнала.
Звено считается заданным и определенным, если известна его передаточная функция или дифференциальное уравнение. Кроме того, звенья имеют временные и частотные характеристики.
Наличие нулевых корней в числителе или знаменателе ПФ типовых звеньев — это признак для разбиения последних на три группы:
Позиционные звенья: 1, 2, 3, 4, 5, — не имеют нулевых корней, и, следовательно, в области низких частот (т.е. в установившемся режиме), имеют коэффициент передачи равный k.
Интегрирующие звенья: 6, 7, 8, — имеют нулевой корень-полюс, и, следовательно, в области низких частот, имеют коэффициент передачи, стремящийся к бесконечности.
Дифференцирующие звенья: 9, 10 — имеют нулевой корень-ноль, и, следовательно, в области низких частот, имеют коэффициент передачи, стремящийся к нулю.
| 6.2. Типы объектов и законы регулирования |
В зависимости от величины самовыравнивания различают три типа объектов управления: устойчивый (с положительным самовыравниванием); нейтральный (с нулевым самовыравниванием); неустойчивый (с отрицательным самовыравниванием). Признаком отрицательного самовыравнивания является отрицательный знак перед самой выходной величиной в левой части дифференциального уравнения или появление отрицательного знака у свободного члена знаменателя передаточной функции (наличие положительного полюса).
Под законом регулирования (управления) понимается алгоритм или функциональная зависимость, определяющая управляющее воздействие u(t) на объект:
u(t) = F(Δ) , где Δ — ошибка регулирования.
Законы регулирования бывают:
— линейные: 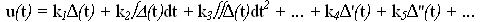
или 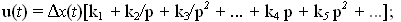
— нелинейные: 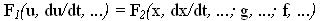
Кроме того, законы регулирования могут быть реализованы в непрерывном виде или в цифровом. Цифровые законы регулирования реализуются путем построения регуляторов с помощью средств вычислительной техники (микро ЭВМ или микропроцессорных систем).
Наличие в (3.1) чувствительности регулятора к пропорциональной, к интегральным или к дифференциальным составляющим в первичной информации x(t), определяет тип регулятора:
1. P — пропорциональный;
2. I — интегральный;
3. PI — пропорционально интегральный (изодромный);
4. PD — пропорционально дифференциальный;
5. и более сложные варианты — PID, PIID, PIDD, .
Нелинейные законы регулирования подразделяются на:
1. функциональные;
2. логические;
3. оптимизирующие;
4. параметрические.
В составе структуры САУ содержится управляющее устройство, которое называется регулятором и выполняет основные функции управления, путем выработки управляющего воздействия U в зависимости от ошибки (отклонения), т.е. U = f(Δ). Закон регулирования определяет вид этой зависимости без учёта инерционности элементов регулятора. Закон регулирования определяет основные качественные и количественные характеристики систем.
| 6.4. Временные характеристики звеньев САУ |
Важнейшей характеристикой САР и её составных элементов являются переходные и импульсные переходные (импульсные) функции.
Аналитическое определение переходных функций и характеристик основано на следующих положениях. Если задана передаточная функция системы или отдельного звена W(р) и известен входной сигнал X(t), то выходной сигнал Y(t) определяется следующим соотношением:
Таким образом, изображение выходного сигнала 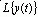
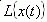
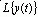
Так как изображение единичного ступенчатого воздействия равно 1/p, то изображение переходной функции определяется соотношением:
Следовательно, для нахождения переходной функции необходимо передаточную функцию разделить на p и выполнять переход от изображения к оригиналу.
Изображение единичного импульса равно 1. Тогда изображение импульсной функции определяется выражением:
Таким образом, передаточная функция является изображением импульсной функции.
Импульсная и переходная функции, как и передаточная функция, являются исчерпывающими характеристиками системы при нулевых начальных условиях. По ним можно определить выходной сигнал при произвольных входных воздействиях.
Таблица 3.1
Изображение по Лапласу и оригиналы
Изображение 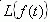 | Оригинал f(t) |
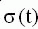 | |
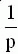 | 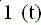 |
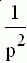 | 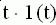 |
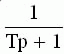 | 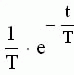 |
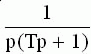 | 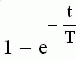 |
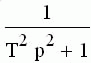 | 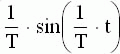 |
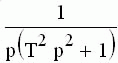 | 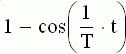 |
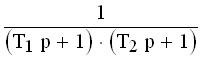 | 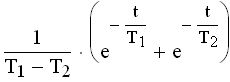 |
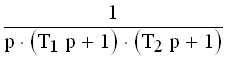 | 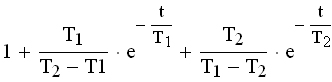 |
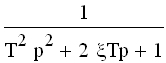 | 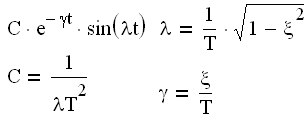 |
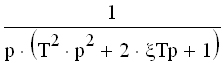 | 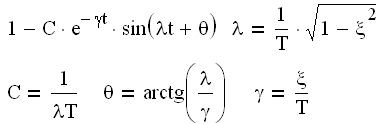 |
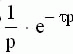 | 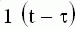 |
Передаточные функции и временные характеристики типовых звеньев приведены в таблице 3.2.
Таблица 3.2
Временные характеристики типовых звеньев
| Тип звена | Передаточные функции | Временные функции | |||
| Позиционные звенья | |||||
| Усилительное | 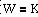 | 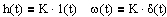 | |||
| Апериодическое 1-го порядка | 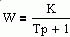 | 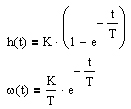 | |||
| Апериодическое 2-го порядка T1≥2T2 | 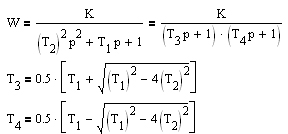 | 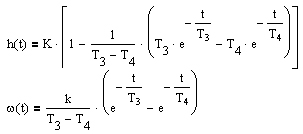 | |||
| Колебательное 0 jφ(ω) (3.2) , где Функция A(ω), представленная при изменении частоты от 0 до
Дата добавления: 2016-06-02 ; просмотров: 5261 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ Типовые звенья линейных САУСТРУКТУРНЫЕ СХЕМЫ ЛИНЕЙНЫХ САУ Типовые звенья линейных САУ Любые сложные САУ могут быть представлены как совокупность более простых элементов (вспомним функциональные и структурные схемы). Поэтому для упрощения исследования процессов в реальных системах они представляются в виде совокупности идеализированных схем, которые точно описываются математически и приближенно характеризуют реальные звенья систем в определенном диапазоне частот сигналов. При составлении структурных схем вводятся некие типовые элементарные звенья (простые, далее не делимые), характеризующиеся только своими передаточными функциями, вне зависимости от их конструктивного исполнения, назначения и принципа действия. Классифицируют их по видам уравнений описывающих их работу. В случае линейных САУ различают следующие типы звеньев: 1.Описываемые линейными алгебраическими уравнениями относительно выходного сигнала: а) пропорциональное (статическое, безынерционное); 2.Описываемые дифференциальными уравнениями первого порядка с постоянными коэффициентами: б) инерционно-дифференцирующее (реальное дифференцирующее); в) инерционное (апериодическое); г) интегрирующее (астатическое); д) интегро-дифференцирующее (упругое). 3.Описываемые дифференциальными уравнениями второго порядка с постоянными коэффициентами: а) инерционное звено второго порядка (апериодическое звено второго порядка, колебательное). Используя математический аппарат, изложенный выше, рассмотрим передаточные функции, переходные и импульсные переходные (весовые) характеристики, а также частотные характеристики этих звеньев. Приведем формулы, которые будут использованы для этой цели. 1. Передаточная функция: 2. Переходная характеристика: 3. Импульсная переходная характеристика : 4. КЧХ: 5. Амплитудная частотная характеристика: где 6. Фазовая частотная характеристика: По этой схеме и исследуем типовые звенья. Заметим, что хотя для некоторых типовых звеньев n (порядок производной выходного параметра в левой части уравнения) равняется m (порядок производной входного параметра в правой части уравнения), а не больше m, как говорилось ранее, однако при конструировании реальных САУ из этих звеньев условие m где k — коэффициент пропорциональности или передачи звена. Примерами такого звена являются: а) клапаны с линеаризованными характеристиками (когда изменение расхода жидкости пропорционально степени изменения положения штока) в рассмотренных выше примерах систем регулирования; б) делитель напряжения; в) рычажная передача и др. Переходя в (3.1) к изображениям, имеем: 1. Передаточная функция: 2. Переходная характеристика: 3. Импульсная переходная характеристика: 4. КЧХ: 5. АЧХ: 6. ФЧХ: Принятое описание связи между входом и выходом справедливо только для идеального звена и соответствует реальным звеньям лишь при низких частотах, Запаздывающее звено. Это звено описывается уравнением где Примером запаздывающего звена служат: а) длинные электрические линии без потерь; б) длинный трубопровод и др. Передаточная функция, переходная и импульсная переходная характеристика, КЧХ, а также АЧХ и ФЧХ этого звена: 1. 2. 3. 4. 5. 6. На рис.3.1 изображены: а) годограф КЧХ запаздывающего звена; б) АЧХ и ФЧХ запаздывающего звена. Заметим, что при увеличении Рис.3.1. Годограф (а) и АЧХ, ФЧХ (б) запаздывающего звена. Интегрирующее звено. Это звено описывается уравнением где Примерами реальных элементов, эквивалентные схемы которых сводятся к интегрирующему звену, являются: а) электрический конденсатор, если считать входным сигналом ток, а выходным – напряжение на конденсаторе: Определим характеристики данного звена: 1. 2. Воспользуемся таблицей преобразования Лапласа 3.1, получаем: Умножаем на 3. 4. 5. 6. На рис.3.2 показаны: а) годограф КЧХ интегрирующего звена; б) АЧХ и ФЧХ звена; в) переходная характеристика звена. Рис.3.2. Годограф (а), АЧХ и ФЧХ (б), переходная характеристика (в) интегрирующего звена. Дифференцирующее звено. Это звено описывается уравнением где Найдем характеристики звена: 1. 2. 3. 4. 5. 6. На рис.3.3 показаны: а) годограф звена; б) АЧХ и ФЧХ звена. Рис. 3.3. Годограф (а), АЧХ и ФЧХ (б) дифференцирующего звена. Примером дифференцирующего звена являются идеальный конденсатор и индуктивность. Это следует из того, что напряжение u и ток i связаны для конденсатора С и индуктивности L соответственно следующими соотношениями: Отметим, что реальная емкость обладает небольшой емкостной индуктивностью, реальная индуктивность имеет межвитковую емкость (которые особенно сильно проявляются на больших частотах), что приводит указанные выше формулы к следующему виду: Таким образом, дифференцирующее звено не может быть технически реализовано, так как порядок правой части его уравнения (3.4) больше порядка левой части. А нам известно, что должно выполняться условие n > m или, в крайнем случае, n = m. Однако можно приблизиться к этому уравнению данного звена, использовав инерционно-дифференцирующее(реальное дифференцирующее)звено. Инерционно-дифференцирующее (реальное дифференцирующее) звено описывается уравнением: где k — коэффициент передачи звена, Т — постоянная времени. Передаточная функция, переходная и импульсная переходная характеристики, КЧХ, АЧХ и ФЧХ этого звена определяются формулами: 1. 2. Используем свойство преобразования Лапласа – смещение изображения (3.20), согласно которому: если Отсюда: 3. 4. 5. 6. На рис.3.4 приведены: а) график КЧХ; б) АЧХ и ФЧХ звена. Рис.3.4. Годограф (а), АЧХ и ФЧХ реального дифференцирующего звена. Для того чтобы свойства реального дифференцирующего звена приближались к свойствам идеального, необходимо одновременно увеличивать коэффициент передачи k и уменьшать постоянную времени Т так, чтобы их произведение оставалось постоянным: где kд – коэффициент передачи дифференцирующего звена. Отсюда видно, что в размерность коэффициента передачи kд дифференцирующего звена входит время. Инерционное звено первого порядка (апериодическое звено) одно из самых распространенных звеньев САУ. Оно описывается уравнением: где k – коэффициент передачи звена, Т – постоянная времени. Характеристики данного звена определяются формулами: 1. 2. Пользуясь свойствами интегрирования оригинала и смещением изображения имеем: 3. 4. 5. 6. На рис.3.5 показаны: а) график КЧХ; б) АЧХ и ФЧХ звена. Рис.3.5. Годограф (а), АЧХ и ФЧХ инерционного звена первого порядка. Интегро-дифференцирующее звено. Это звено описывается дифференциальным уравнением первого порядка в наиболее общем виде: где k — коэффициент передачи звена, Т1 и Т2 — постоянные времени. В зависимости от значения t звено будет обладать различными свойствами. Если Определим характеристики интегродифференцирующего звена: 1. 2. 3. 4. 5. 6. На рис.3.6. приведены: а) график КЧХ; б) АЧХ; в) ФЧХ; г) переходная характеристика звена. Рис.3.6. Годограф (а), АЧХ (б), ФЧХ (в), переходная характеристика (г) интегродифференцирующего звена. Инерционное звено второго порядка. Это звено описывается дифференциальным уравнением второго порядка: где Реакция системы, описываемой уравнением (3.8), на единичное ступенчатое воздействие при Примером конструктивного выполнения данного звена могут служить: а) электрический колебательный контур, содержащий емкость, индуктивность и омическое сопротивление; б) масса, подвешенная на пружине и имеющая демпфирующее устройство, и т.д. Определим характеристики инерционного звена второго порядка: 1. 2. Корни характеристического уравнения стоящего в знаменателе определяются: Очевидно, что здесь возможно три случая: 1) при 2) при 3) при переходная характеристика определяется формулой: т.е., как отмечалось выше, она приобретает колебательный характер. 3. Также имеем три случая: 1) т.к. 2) 3) 4. 5. 6. где а = 0 при Рис.3.7. График КЧХ (а) и переходная характеристика (б) звена. На рис.3.7, а, б показан типичный вид КЧХ и переходных характеристик для случаев На рис.3.8 показаны соответствующие АЧХ и ФЧХ. Здесь Рис.3.8. АЧХ (а) и ФЧХ (б) звена. Как видим, колебательному характеру переходной характеристики соответствует наличие в графике АЧХ резонансного пика при частоте резонанса Продифференцируем выражение для АЧХ этого звена по Из (3.11) следует, что при Подстановка (3.11) и выражения для АЧХ в (3.10) приводит к следующей формуле для определения частотного показателя колебательности: Об интенсивности затухания колебаний можно судить также и по корневому показателю колебательности, который равен отношению абсолютного значения вещественной части корней к их мнимой части: С учетом (3.9) корневой показатель колебательности т рассматриваемого звена можно выразить через коэффициенты его уравнения: Приняв во внимание (3.12), можно установить связь т с частотным показателем колебательности M: На практике интенсивность затухания колебаний в колебательном звене удобно характеризовать относительным уменьшением соседних амплитуд Этот показатель получил название степени затуханияколебаний. Поскольку переходная характеристика колебательного звена определяется формулой: то можно записать: где С учетом этого формулу (3.15) можно представить следующим образом: Таким образом, степень затухания однозначно связана с корневым показателем колебательности т,а, следовательно, и с частотным показателем колебательности М. источники: http://helpiks.org/8-26327.html http://lektsii.org/14-69681.html |

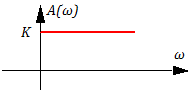








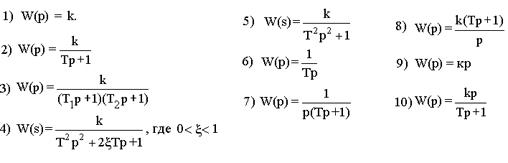
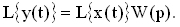
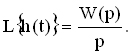
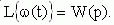
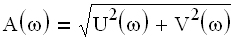 — модуль;
— модуль; 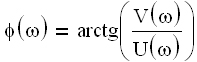 — аргумент частотной передаточной функции.
— аргумент частотной передаточной функции. получило название амплитудной частотной характеристики (АЧХ).
получило название амплитудной частотной характеристики (АЧХ).  раз. Верхняя полуплоскость л.а.х. соответствует значениям А>1 (усиление амплитуды), а нижняя полуплоскость — значениям А 0, r>0, T>0, 0
раз. Верхняя полуплоскость л.а.х. соответствует значениям А>1 (усиление амплитуды), а нижняя полуплоскость — значениям А 0, r>0, T>0, 0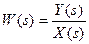 .
.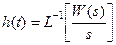 .
.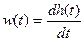 или
или  .
. .
. ,
, ,
,  .
. .
. (3.1)
(3.1) .
.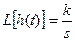 , следовательно
, следовательно  .
.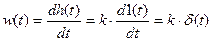 .
. .
. .
. .
. . При
. При  в реальных звеньях коэффициент передачи k начинает зависеть от частоты и при высоких частотах падает до нуля.
в реальных звеньях коэффициент передачи k начинает зависеть от частоты и при высоких частотах падает до нуля. , (3.2)
, (3.2) – время запаздывания.
– время запаздывания. .
. , значит:
, значит:  .
.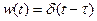 .
. .
. .
. .
. конец вектора
конец вектора 

 .
. — коэффициент передачи звена.
— коэффициент передачи звена. ; б) вращающийся вал, если считать входным сигналом угловую скорость вращения, а выходным – угол поворота вала:
; б) вращающийся вал, если считать входным сигналом угловую скорость вращения, а выходным – угол поворота вала:  ; и т.д.
; и т.д. .
. .
. .
. так как функция
так как функция  при
при  .
. .
. .
. .
. .
.
 , (3.4)
, (3.4) – коэффициент передачи звена.
– коэффициент передачи звена.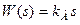 .
. , учитывая, что
, учитывая, что  , находим:
, находим:  .
. .
.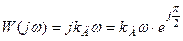 .
. .
. .
.
 ,
,  .
. ,
, 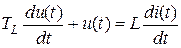 .
.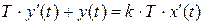 , (3.5)
, (3.5) .
. .
. , то
, то  .
. .
. .
. .
. .
. .
.
 , (3.6)
, (3.6) .
. .
. .
. , т.к.
, т.к.  при
при  , то на всей временной оси данная функция равна 0 (
, то на всей временной оси данная функция равна 0 (  при
при  ).
).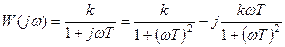 .
.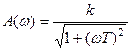 .
. .
.
 , (3.7)
, (3.7) .
. , то звено по своим свойствам будет приближаться к интегрирующему и инерционному звеньям. Если
, то звено по своим свойствам будет приближаться к интегрирующему и инерционному звеньям. Если  , то данное звено по свойствам будет ближе к дифференцирующему и инерционно-дифференцирующему.
, то данное звено по свойствам будет ближе к дифференцирующему и инерционно-дифференцирующему. .
. , отсюда следует:
, отсюда следует: .
.
 , т.к.
, т.к.  при t ® 0, то:
при t ® 0, то: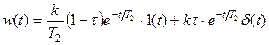 .
. .
. .
. .
.

 , (3.8)
, (3.8) (капа) – постоянная затухания; Т — постоянная времени, k — коэффициент передачи звена.
(капа) – постоянная затухания; Т — постоянная времени, k — коэффициент передачи звена. представляет собой затухающие гармонические колебания, в этом случае звено еще называется колебательным. При
представляет собой затухающие гармонические колебания, в этом случае звено еще называется колебательным. При  колебания не возникнут, и звено, описываемое уравнением (3.8) называется апериодическим звеном второго порядка. Если
колебания не возникнут, и звено, описываемое уравнением (3.8) называется апериодическим звеном второго порядка. Если  , то колебания будут незатухающими с частотой
, то колебания будут незатухающими с частотой  .
. .
. .
.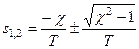 .
. корни характеристического уравнения отрицательные вещественные разные
корни характеристического уравнения отрицательные вещественные разные  и
и  , тогда переходная характеристика определяется:
, тогда переходная характеристика определяется: ;
; корни характеристического уравнения отрицательные вещественные одинаковые
корни характеристического уравнения отрицательные вещественные одинаковые 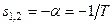 :
: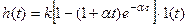 ;
; корни характеристического уравнения звена являются комплексно—сопряженными
корни характеристического уравнения звена являются комплексно—сопряженными  , причем
, причем ,
,  , (3.9)
, (3.9) ,
, ,
, при
при  ;
; , т.к.
, т.к.  при
при  , т.к.
, т.к.  при
при  .
. .
. ,
, и а = 1 при
и а = 1 при 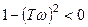 (см. формулу (3.77)).
(см. формулу (3.77)).
 и
и  до
до  при
при  (приближаемся слева, т.е.
(приближаемся слева, т.е.  и
и  ) и вторая от
) и вторая от  при
при  и
и  ) до
) до  при
при  .
. – безразмерная частота.
– безразмерная частота.
 . Отношение максимального (пикового) значения АЧХ к ее значению при нулевой частоте получило название частотного показателя колебательности:
. Отношение максимального (пикового) значения АЧХ к ее значению при нулевой частоте получило название частотного показателя колебательности: . (3.10)
. (3.10) при условии
при условии  , (3.11)
, (3.11) резонансная частота
резонансная частота  , а, согласно формуле для АЧХ, при этом
, а, согласно формуле для АЧХ, при этом  .
. при условии
при условии 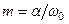 .
. . (3.13)
. (3.13) . (3.14)
. (3.14) и
и  переходной характеристики (рис.3.7, б):
переходной характеристики (рис.3.7, б): . (3.15)
. (3.15) , (3.16)
, (3.16) — период собственных колебаний звена.
— период собственных колебаний звена. . (3.17)
. (3.17)