Типы линий и их канонические уравнения

Уравнение прямой, виды уравнения прямой на плоскости

В прошлом материале мы рассмотрели основные моменты, касающиеся темы прямой на плоскости. Теперь же перейдем к изучению уравнения прямой: рассмотрим, какое уравнение может называться уравнением прямой, а также то, какой вид имеет уравнение прямой на плоскости.

Определение уравнения прямой на плоскости

Допустим, что есть прямая линия, которая задана в прямоугольной декартовой системе координат O х у .

Прямая линия – это геометрическая фигура, которая состоит из точек. Каждая точка имеет свои координаты по осям абсцисс и ординат. Уравнение, которое описывает зависимость координат каждой точки прямой в декартовой системе O x y , называется уравнением прямой на плоскости.

Фактически, уравнение прямой на плоскости – это уравнение с двумя переменными, которые обозначаются как x и y . Уравнение обращается в тождество при подстановке в него значений любой из точек прямой линии.

Давайте посмотрим, какой вид будет иметь уравнение прямой на плоскости. Этому будет посвящен весь следующий раздел нашей статьи. Отметим, что существует несколько вариантов записи уравнения прямой. Объясняется это наличием нескольких способов задания прямой линии на плоскости, и также различной спецификой задач.

Общее уравнение прямой линии

Познакомимся с теоремой, которая задает вид уравнения прямой линии на плоскости в декартовой системе координат O x y .

Уравнение вида A x + B y + C = 0 , где x и y – переменные, а А , В и C – это некоторые действительные числа, из которых A и B не равны нулю, задает прямую линию в декартовой системе координат O x y . В свою очередь, любая прямая линия на плоскости может быть задана уравнением вида A x + B y + C = 0 .

Таким образом, общее уравнение прямой на плоскости имеет вид A x + B y + C = 0 .

Поясним некоторые важные аспекты темы.

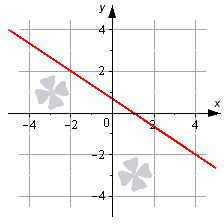
Посмотрите на рисунок.

Линия на чертеже определяется уравнением вида 2 x + 3 y — 2 = 0 , так как координаты любой точки, составляющей эту прямую, удовлетворяют приведенному уравнению. В то же время, определенное количество точек плоскости, определяемых уравнением 2 x + 3 y — 2 = 0 , дают нам прямую линию, которую мы видим на рисунке.

Общее уравнение прямой может быть полным и неполным. В полном уравнении все числа А , В и C отличны от нуля. Во всех остальных случаях уравнение считается неполным. Уравнение вида A x + B y = 0 определяет прямую линию, которая проходит через начало координат. Если A равно нулю, то уравнение A x + B y + C = 0 задает прямую, расположенную параллельно оси абсцисс O x . Если B равно нулю, то линия параллельна оси ординат O y .

Вывод: при некотором наборе значений чисел А , В и C с помощью общего уравнения прямой можно записать любую прямую линию на плоскости в прямоугольной системе координат O х у .

Прямая, заданная уравнением вида A x + B y + C = 0 , имеет нормальный вектор прямой с координатами A , B .

Все приведенные уравнения прямых, которые мы рассмотрим ниже, могут быть получены из общего уравнения прямой. Также возможен и обратный процесс, когда любое из рассматриваемых уравнений может быть приведено к общему уравнению прямой.

Разобраться во всех нюансах темы можно в статье «Общее уравнение прямой». В материале мы приводим доказательство теоремы с графическими иллюстрациями и подробным разбором примеров. Особое внимание в статье уделяется переходам от общего уравнения прямой к уравнениям других видов и обратно.

Уравнение прямой в отрезках

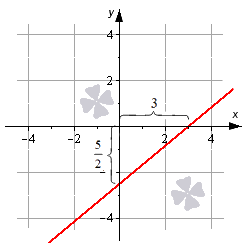
Уравнение прямой в отрезках имеет вид x a + y b = 1 , где a и b – это некоторые действительные числа, которые не равны нулю. Абсолютные величины чисел a и b равны длине отрезков, которые отсекаются прямой линией на осях координат. Длина отрезков отсчитывается от начала координат.

Благодаря уравнению можно легко построить прямую линию на чертеже. Для этого необходимо отметить в прямоугольной системе координат точки a , 0 и 0 , b , а затем соединить их прямой линией.

Построим прямую, которая задана формулой x 3 + y — 5 2 = 1 . Отмечаем на графике две точки 3 , 0 , 0 , — 5 2 , соединяем их между собой.

Дополнительно рекомендуем ознакомиться с материалом, изложенным в статье «Уравнение прямой в отрезках».

Уравнение прямой с угловым коэффициентом

Эти уравнения, имеющие вид y = k · x + b должны быть нам хорошо известны из курса алгебры. Здесь x и y – это переменные, k и b – это некоторые действительные числа, из которых k представляет собой угловой коэффициент. В этих уравнениях переменная у является функцией аргумента x .

Дадим определение углового коэффициента через определение угла наклона прямой к положительному направлению оси O x .

Для обозначения угла наклона прямой к положительному направлению оси O x в декартовой системе координат введем величину угла α . Угол отсчитывается от положительного направления оси абсцисс до прямой линии против хода часовой стрелки. Угол α считается равным нулю в том случае, если линия параллельна оси O x или совпадает с ней.

Угловой коэффициент прямой – это тангенс угла наклона этой прямой. Записывается это следующим образом k = t g α . Для прямой, которая располагается параллельно оси O y или совпадает с ней, записать уравнение прямой с угловым коэффициентом не представляется возможным, так как угловой коэффициент в этом случае превращается в бесконечность (не существует).

Прямая, которая задана уравнением y = k · x + b , проходит через точку 0 , b на оси ординат. Это значит, что уравнение прямой с угловым коэффициентом y = k · x + b , задает на плоскости прямую линию, которая проходит через точку 0 , b и образует угол α с положительным направлением оси O x , причем k = t g α .

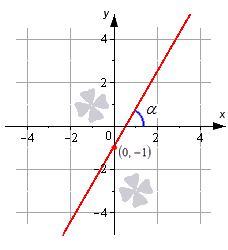
Изобразим прямую линию, которая определяется уравнением вида y = 3 · x — 1 .

Эта линия должна пройти через точку ( 0 , — 1 ) . Угол наклона α = a r c t g 3 = π 3 равен 60 градусов к положительному направлению оси O x . Угловой коэффициент равен 3

Обращаем ваше внимание, что с помощью уравнения прямой с угловым коэффициентом очень удобно искать уравнение касательной к графику функции в точке.

Больше материала по теме можно найти в статье «Уравнение прямой с угловым коэффициентом». Помимо теории там размещено большое количество графических примеров и подробный разбор задач.

Каноническое уравнение прямой на плоскости

Данный вид уравнения имеет вид x — x 1 a x = y — y 1 a y , где x 1 , y 1 , a x , a y — это некоторые действительные числа, из которых a x и a y не равны нулю.

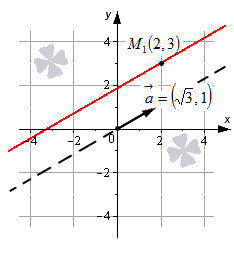
Прямая линия, заданная каноническим уравнением прямой, проходит через точку M 1 ( x 1 , y 1 ) . Числа a x и a y в знаменателях дробей представляют собой координаты направляющего вектора прямой линии. Это значит, что каноническое уравнение прямой линии x — x 1 a x = y — y 1 a y в декартовой системе координат O x y соответствует линии, проходящей через точку M 1 ( x 1 , y 1 ) и имеющей направляющий вектор a → = ( a x , a y ) .

Изобразим в системе координат O x y прямую линию, которая задается уравнением x — 2 3 = y — 3 1 . Точка M 1 ( 2 , 3 ) принадлежит прямой, вектор a → ( 3 , 1 ) является направляющим вектором этой прямой линии.

Каноническое уравнение прямой линии вида x — x 1 a x = y — y 1 a y может быть использовано в случаях, когда a x или a y равно нулю. Наличие ноля в знаменателе делает запись x — x 1 a x = y — y 1 a y условной. Уравнение можно записать следующим образом a y ( x — x 1 ) = a x ( y — y 1 ) .

В том случае, когда a x = 0 , каноническое уравнение прямой принимает вид x — x 1 0 = y — y 1 a y и задает прямую линию, которая расположена параллельно оси ординат или совпадает с этой осью.

Каноническое уравнение прямой при условии, что a y = 0 , принимает вид x — x 1 a x = y — y 1 0 . Такое уравнение задает прямую линию, расположенную параллельно оси абсцисс или совпадающую с ней.

Больше материала на тему канонического уравнения прямой смотрите здесь. В статье мы приводим целый ряд решений задач, а также многочисленные примеры, которые позволяют лучше овладеть темой.

Параметрические уравнения прямой на плоскости

Данные уравнения имеют вид x = x 1 + a x · λ y = y 1 + a y · λ , где x 1 , y 1 , a x , a y — это некоторые действительные числа, из которых a x и a y не могут быть одновременно равны нулю. В формулу вводится дополнительный параметр λ , который может принимать любые действительные значения.

Назначение параметрического уравнения в том, чтобы установить неявную зависимости между координатами точек прямой линии. Для этого и вводится параметр λ .

Числа x , y представляют собой координаты некоторой точки прямой. Они вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра λ .

Предположим, что λ = 0 .

Тогда x = x 1 + a x · 0 y = y 1 + a y · 0 ⇔ x = x 1 y = y 1 , т. е. точка с координатами ( x 1 , y 1 ) принадлежит прямой.

Обращаем ваше внимание на то, что коэффициенты a x и a y при параметре λ в данном виде уравнений представляют собой координаты направляющего вектора прямой линии.

Рассмотрим параметрические уравнения прямой линии вида x = 2 + 3 · λ y = 3 + λ . Прямая, заданная уравнениями, в декартовой системе координат проходит через точку ( x 1 , y 1 ) и имеет направляющий вектор a → = ( 3 , 1 ) .

Больше информации ищите в статье «Параметрические уравнения прямой на плоскости».

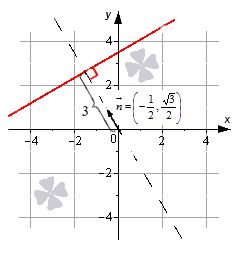
Нормальное уравнение прямой

Нормальное уравнение прямой имеет вид , A x + B y + C = 0 , где числа А , В , и C таковы, что длина вектора n → = ( A , B ) равна единице, а C ≤ 0 .

Нормальным вектором линии, заданной нормальным уравнением прямой в прямоугольной системе координат O х у , является вектор n → = ( A , B ) . Эта прямая проходит на расстоянии C от начала координат в направлении вектора n → = ( A , B ) .

Еще одним вариантом записи нормального уравнения прямой линии является cos α · x + cos β · y — p = 0 , где cos α и cos β — это два действительных числа, которые представляют собой направляющие косинусы нормального вектора прямой единичной длины. Это значит, что n → = ( cos α , cos β ) , справедливо равенство n → = cos 2 α + cos 2 β = 1 , величина p ≥ 0 и равна расстоянию от начала координат до прямой.

Рассмотрим общее уравнение прямой — 1 2 · x + 3 2 · y — 3 = 0 . Это общее уравнение прямой является нормальным уравнением прямой, так как n → = A 2 + B 2 = — 1 2 2 + 3 2 = 1 и C = — 3 ≤ 0 .

Уравнение задает в декартовой системе координат 0ху прямую линию, нормальный вектор которой имеет координаты — 1 2 , 3 2 . Линия удалена от начала координат на 3 единицы в направлении нормального вектора n → = — 1 2 , 3 2 .

Обращаем ваше внимание на то, что нормальное уравнение прямой на плоскости позволяет находить расстояние от точки до прямой на плоскости.

Если в общем уравнении прямой A x + B y + C = 0 числа А , В и С таковы, что уравнение A x + B y + C = 0 не является нормальным уравнением прямой, то его можно привести к нормальному виду. Подробнее об этом читайте в статье «Нормальное уравнение прямой».

Лекция Линии на плоскости и их уравнения

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Лекция № 7. Тема 1 : Линии на плоскости и их уравнения

1.1. Линии и их уравнения в декартовой системе координат

В аналитической геометрии линии на плоскости рассматриваются как геометрическое место точек (г. м.т.), обладающих одинаковым свойством, общим для всех точек линии.

О пределение. Уравнение линии – это уравнение с двумя переменными х и у , которому удовлетворяют координаты любой точки линии и не удовлетворяют координаты никакой другой точки, не лежащей на данной линии.

Верно и обратное, т.е. любое уравнение у

вида , вообще говоря, в декартовой

системе координат (ДСК) определяет линию

как г.м.т., координаты которых удовлетворяют

этому уравнению. О х

Замечание 1. Не всякое уравнение вида определяет линию. Например, для уравнения не существует точек, координаты, которых удовлетворяли бы этому уравнению. Такие случаи в дальнейшем рассматривать не будем. Это случай так называемых мнимых линий.

П ример 1. Составить уравнение окружности радиуса R с центром в точке .

Для любой точки , лежащей у М

на окружности, в силу определения R

окружности как г.м.т., равноудаленных

от точки , получаем уравнение х

.

1.2. Параметрические уравнения линий

Существует ещё один способ задавать линию на плоскости при помощи уравнений, которые называются параметрическими :

Пример 1. Линия задана параметрическими уравнениями

Требуется получить уравнение этой линии в ДСК.

Исключим параметр t . Для этого возведём обе части этих уравнений в квадрат и сложим

Пример 2. Линия задана параметрическими уравнениями

а

Требуется получить уравнение

этой линии в ДСК. — а а

Поступим аналогично, тогда получим

— а

Замечание 2. Следует отметить, что параметром t в механике явля-ется время.

1.3. Уравнение линии в полярной системе координат

ДСК является не единственным способом определять положение точки и, следовательно, задавать уравнение линии. На плоскости часто целесо-образно использовать так называемую полярную систему координат (ПСК).

П СК будет определена, если задать точку О – полюс и луч ОР , исхо-дящий из этой точки, который называется полярной осью. Тогда положение любой точки определяется двумя числами: полярным радиусом и полярным углом – угол между

полярной осью и полярным радиусом.

Положительное направление отсчета

полярного угла от полярной оси

считается против часовой стрелки.

Для всех точек плоскости , О Р

а для однозначности полярного угла считается .

Если начало ДСК совместить с

полюсом, а ось Ох направить по

полярной оси, то легко убедиться у

в связи между полярными и

декартовыми координатами:

О х Р

(1)

Если уравнение линии в ДСК имеет вид , то в ПСК — Тогда из этого уравнения можно получить урав-нение в виде

Пример 3. Составить уравнение окружности в ПСК, если центр окружности находится в полюсе.

Используя формулы перехода (1) от ДСК к ПСК, получим

Пример 4. Составить уравнение окружности,

если полюс на окружности, а полярная ось у

проходит через диаметр.

Поступим аналогично

О 2 R х

R

Данное уравнение можно получить и

из геометрических представлений (см. рис.).

П ример 5. Построить график линии

Перейдём к ПСК. Уравнение

примет вид О

График линии построим с а

учётом его симметрии и ОДЗ

функции:

Данная линия называется лемнискатой Бернулли .

1.4. Преобразование системы координат.

Уравнение линии в новой системе координат

1. Параллельный перенос ДСК. у

Рассмотрим две ДСК, имеющие М

одинаковое направление осей, но

различные начала координат.

В системе координат Оху точка

относительно системы О х

имеет координаты . Тогда имеем

и

В координатной форме полученное векторное равенство имеет вид

или . (2)

Формулы (2) представляют собой формулы перехода от «старой» системы координат Оху к «новой» системе координат и наоборот.

Пример 5. Получить уравнение окружности выполнив параллельный перенос системы координат в центр окружности.

И з формул (2) следует у

2. Поворот системы координат. М

Рассмотрим две системы координат

с общим началом, но с различными

направлениями осей. В системе коор-

динат Оху вектор , О х

а в системе координат вектор

.

Разложим векторы по базису :

Тогда имеем ,

откуда, переходя к координатной форме, получим формулы перехода

(3) (4)

Формулы (3) представляют собой переход от «старой» системы координат Оху к «новой» системе , а формулы (4) – наоборот.

Пример 6. Составить уравнение гиперболы при повороте системы координат на угол .

Используя формулы (3), получаем

или (каноническое уравнение гиперболы).

3. Общий случай: поворот вместе с параллельным переносом осущест-вляется согласно формулам (2) и (3):

(5)

Для того, чтобы получить уравнение линии в новой системе координат, необходимо в это уравнение подставить формулы (5).

Мнимые прямые. Линии второго порядка

8.3.15. Точка А лежит на прямой . Расстояние от точки А до плоскости

8.3.16. Составьте уравнение прямой, симметричной прямой

относительно плоскости .

8.3.17. Составьте уравнения проекций на плоскость следующих прямых:

а) ;

б)

в) .

8.3.18. Найдите угол между плоскостью и прямой:

а) ;

б) .

8.3.19. Найдите точку, симметричную точке относительно плоскости, проходящей через прямые:

и

8.3.20. Точка А лежит на прямой

Расстояние от точки А до прямой равно . Найдите координаты точки А.

§ 8.4. КРИВЫЕ ВТОРОГО ПОРЯДКА

Установим на плоскости прямоугольную систему координат и рассмотрим общее уравнение второй степени

в котором .

Множество всех точек плоскости, координаты которых удовлетворяют уравнению (8.4.1), называется кривой (линией ) второго порядка .

Для всякой кривой второго порядка существует прямоугольная система координат, называемая канонической, в которой уравнение этой кривой имеет один из следующих видов:

1) (эллипс);

2) (мнимый эллипс);

3) (пара мнимых пересекающихся прямых);

4) (гипербола);

5) (пара пересекающихся прямых);

6) (парабола);

7) (пара параллельных прямых);

8) (пара мнимых параллельных прямых);

9) (пара совпадающих прямых).

Уравнения 1) – 9) называются каноническими уравнениями кривых второго порядка.

Решение задачи приведения уравнения кривой второго порядка к каноническому виду включает нахождение канонического уравнения кривой и канонической системы координат. Приведение к каноническому виду позволяет вычислить параметры кривой и определить ее расположение относительно исходной системы координат. Переход от исходной прямоугольной системы координат к канонической осуществляется путем поворота осей исходной системы координат вокруг точки О на некоторый угол j и последующего параллельного переноса системы координат.

Инвариантами кривой второго порядка (8.4.1) называются такие функции от коэффициентов ее уравнения, значения которых не меняются при переходе от одной прямоугольной системы координат к другой такой же системе.

Для кривой второго порядка (8.4.1) сумма коэффициентов при квадратах координат

,

определитель, составленный из коэффициентов при старших членах

и определитель третьего порядка

Значение инвариантов s, d, D можно использовать для определения типа и составления канонического уравнения кривой второго порядка.

Классификация кривых второго порядка, основанная на инвариантах

Кривая эллиптического типа

sD 0. Мнимый эллипс

Пара мнимых прямых, пересекающихся в действительной точке

Кривая гиперболического типа

Пара пересекающихся прямых

Кривая параболического типа

Пара параллельных прямых (различных, мнимых или совпадающих)

Рассмотрим подробнее эллипс, гиперболу и параболу.

Эллипсом (рис. 8.1) называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек этой плоскости, называемых фокусами эллипса , есть величина постоянная (большая, чем расстояние между фокусами). При этом не исключается совпадение фокусов эллипса. Если фокусы совпадают, то эллипс представляет собой окружность.

Полусумму расстояний от точки эллипса до его фокусов обозначают через а, половину расстояний между фокусами – с. Если прямоугольная система координат на плоскости выбрана так, что фокусы эллипса располагаются на оси Оx симметрично относительно начала координат, то в этой системе координат эллипс задается уравнением

, (8.4.2)

называемым каноническим уравнением эллипса , где .

Рис. 8.1

При указанном выборе прямоугольной системы координат эллипс симметричен относительно осей координат и начала координат. Оси симметрии эллипса называют его осями , а центрего симметрии – центром эллипса . Вместе с тем часто осями эллипса называют числа 2a и 2b, а числа a и b – большой и малой полуосью соответственно.

Точки пересечения эллипса с его осями называются вершинами эллипса . Вершины эллипса имеет координаты (а,0), (–а,0), (0,b), (0,–b).

Эксцентриситетом эллипса называется число

.

Отсюда видно, что эксцентриситет характеризует форму эллипса: чем ближе e к нулю, тем больше эллипс похож на окружность; при увеличении e эллипс становится более вытянутым.

Чтобы пояснить это на конкретном примере, покажу вам, что соответствует в этой интерпретации следующему утверждению: (действительная или мнимая) точка Р лежит на (действительной или мнимой) прямой g. При этом, конечно, приходится различать такие случаи:

1) действительная точка и действительная прямая,

2) действительная точка и мнимая прямая,

Случай 1) не требует от нас особых разъяснений; здесь перед нами одно из основных соотношений обычной геометрии.

В случае 2) через заданную действительную точку обязательно должна проходить наряду с заданной мнимой прямой также и комплексно сопряженная с нею прямая; следовательно, эта точка должна совпадать с вершиной того пучка лучей, которым мы пользуемся для изображения мнимой прямой.

Подобно этому в случае 3) действительная прямая должна быть тождественна с носителем той прямолинейной инволюции точек, которая служит представителем заданной мнимой точки.

Наиболее интересным является случай 4) (рис. 96): здесь, очевидно, комплексно сопряженная точка должна также лежать на комплексно сопряженной прямой, а отсюда следует, что каждая пара точек инволюции точек, изображающей точку Р, должна находиться на некоторой паре прямых инволюции прямых, изображающей прямую g, т. е. что обе эти инволюции должны быть расположены перспективно одна относительно другой; кроме того, оказывается, что и стрелки обеих инволюций также расположены перспективно.

Вообще, в аналитической геометрии плоскости, уделяющей внимание также и комплексной области, мы получим полную действительную картину этой плоскости, если к совокупности всех ее действительных точек и прямых присоединим в качестве новых элементов совокупность рассмотренных выше инволюционных фигур вместе со стрелками их направлений. Здесь будет достаточно, если я намечу в общих очертаниях, какой вид приняло бы при этом построение такой действительной картины комплексной геометрии. При этом я буду следовать тому порядку, в котором теперь обычно излагают первые предложения элементарной геометрии.

1) Начинают с аксиом существования, назначение которых — дать точную формулировку наличия только что упомянутых элементов в расширенной по сравнению с обычной геометрией области.

2) Затем аксиомы соединения, которые утверждают, что также и в определенной в п. 1) расширенной области! через (каждые) две точки проходит одна и только одна прямая и что (всякие) две прямые имеют одну и только одну общую точку.

При этом подобно тому, что мы имели выше, приходится каждый раз различать четыре случая в зависимости от того, являются ли действительными заданные элементы, и представляется очень интересным точно продумать, какие именно действительные построения с инволюциями точек и прямых служат изображением этих комплексных соотношений.

3) Что же касается аксиом расположения (порядка), то здесь по сравнению с действительными соотношениями выступают на сцену совершенно новые обстоятельства; в частности, все действительные и комплексные точки, лежащие на одной фиксированной прямой, а также все лучи, проходящие через одну фиксированную точку, образуют двумерный континуум. Ведь каждый из нас вынес из изучения теории функций привычку изображать совокупность значений комплексной переменной всеми точками плоскости.

4) Наконец, что касается аксиом непрерывности, то я укажу здесь только, как изображаются комплексные точки, лежащие как угодно близко к какой-нибудь действительной точке. Для этого через взятую действительную точку Р (или через какую-нибудь другую близкую к ней действительную точку) нужно провести какую-нибудь прямую и рассмотреть на ней такие две разделяющие одна другую (т. е. лежащие «скрещенным образом») пары точек (рис. 97), чтобы две точки взятые из разных пар, лежали близко одна к другой и к точке Р; если теперь неограниченно сближать точки то инволюция, определяемая названными парами точек, вырождается, т. е. обе ее до сих пор комплексные двойные точки совпадают с точкой Каждая из обеих мнимых точек, изображаемых этой инволюцией (вместе с той или другой стрелкой), переходит, следовательно, непрерывно в некоторую точку, близкую к точке Р, или даже непосредственно в точку Р. Конечно, для того чтобы быть в состоянии с пользой применять эти представления о непрерывности, необходимо детально с ними поработать.

Хотя все это построение и является по сравнению с обычной действительной геометрией достаточно громоздким и утомительным, но зато оно может дать несравненно больше. В частности, оно способно поднять на уровень полной геометрической наглядности алгебраические образы, понимаемые как совокупности их действительных и комплексных элементов, и при его помощи можно наглядно уяснить себе на самих фигурах такие теоремы, как основная теорема алгебры или теорема Безу о том, что две кривые порядков имеют, вообще говоря, ровно общих точек. Для этой цели следовало бы, конечно, осмыслить основные положения в значительно более точной и наглядной форме, чем это было сделано до сих пор; впрочем, в литературе уже имеется весь существенно необходимый для таких исследований материал.

Но в большинстве случаев применение этого геометрического толкования привело бы все же при всех его теоретических преимуществах к таким усложнениям, что приходится довольствоваться его принципиальной возможностью и возвращаться фактически к более наивной точке зрения, заключающейся в следующем: комплексная точка есть совокупность трех комплексных координат, и с нею можно оперировать точно так же, как и с действительными точками. В самом деле, такое введение мнимых элементов, воздерживающееся от каких бы то ни было принципиальных рассуждений, всегда оказывалось плодотворным в тех случаях, когда нам приходилось иметь дело с мнимыми циклическими точками или с окружностью сфер. Как уже было сказано, впервые стал пользоваться мнимыми элементами в этом смысле Понселе; его последователями в этом отношении были другие французские геометры, главным образом Шаль и Дарбу; в Германии ряд геометров, в особенности Ли, также применяли с большим успехом такое понимание мнимых элементов.

Этим отступлением в область мнимого я заканчиваю весь второй отдел моего курса и обращаюсь к новой главе,

Линии второго порядка

плоские линии, декартовы прямоугольные координаты которых удовлетворяют алгебраическому уравнению 2-й степени

a 11 x 2 + a 12 xy + a 22 y 2 + 2a 13 x + 2a 23 y + a 11 = 0. (*)

Уравнение (*) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую Л. в. п. В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса начала и поворота системы координат на некоторый угол к одному из 9 приведённых ниже канонических видов, каждому из которых соответствует определённый класс линий. Именно,

y 2 = 2px — параболы,

x 2 — а 2 = 0 — пары параллельных прямых,

x 2 + а 2 = 0 — пары мнимых параллельных прямых,

x 2 = 0 — пары совпадающих параллельных прямых.

Исследование вида Л. в. п. может быть проведено без приведения общего уравнения к каноническому виду. Это достигается совместным рассмотрением значений т. н. основных инвариантов Л. в. п. — выражений, составленных из коэффициентов уравнения (*), значения которых не меняются при параллельном переносе и повороте системы координат:

S = a 11 + a 22 , (a ij = a ji ).

Так, например, эллипсы, как нераспадающиеся линии, характеризуются тем, что для них Δ ≠ 0; положительное значение инварианта δ выделяет эллипсы среди других типов нераспадающихся линий (для гипербол δ

Три основные инварианта Δ, δ и S определяют Л. в. п. (кроме случая параллельных прямых) с точностью до движения (См. Движение) евклидовой плоскости: если соответствующие инварианты Δ, δ и S двух линий равны, то такие линии могут быть совмещены движением. Иными словами, эти линии эквивалентны по отношению к группе движений плоскости (метрически эквивалентны).

Существуют классификации Л. в. п. с точки зрения др. групп преобразований. Так, относительно более общей, чем группа движений, — группы аффинных преобразований (См. Аффинные преобразования) — эквивалентными являются любые две линии, определяемые уравнениями одного канонического вида. Например, две подобные Л. в. п. (см. Подобие) считаются эквивалентными. Связи между различными аффинными классами Л. в. п. позволяет установить классификация с точки зрения проективной геометрии (См. Проективная геометрия), в которой бесконечно удалённые элементы не играют особой роли. Действительные нераспадающиеся Л. в. п.: эллипсы, гиперболы и параболы образуют один проективный класс — класс действительных овальных линий (овалов). Действительная овальная линия является эллипсом, гиперболой или параболой в зависимости от того, как она расположена относительно бесконечно удалённой прямой: эллипс пересекает несобственную прямую в двух мнимых точках, гипербола — в двух различных действительных точках, парабола касается несобственной прямой; существуют проективные преобразования, переводящие эти линии одна в другую. Имеется всего 5 проективных классов эквивалентности Л. в. п. Именно,

(x 1 , x 2 , x 3 — однородные координаты):

x 1 2 + x 2 2 — x 3 2 = 0 — действительный овал,

x 1 2 + x 2 2 + x 3 2 = 0 — мнимый овал,

x 1 2 — x 2 2 = 0 — пара действительных прямых,

x 1 2 + x 2 2 = 0 — пара мнимых прямых,

x 1 2 = 0 — пара совпадающих действительных прямых.

Большая советская энциклопедия. — М.: Советская энциклопедия . 1969-1978 .

Смотреть что такое «Линии второго порядка» в других словарях:

Плоские линии, прямоугольные координаты точек которых удовлетворяют алгебраическому уравнению 2 й степени. Среди линий второго порядка эллипсы (в частности, окружности), гиперболы, параболы … Большой Энциклопедический словарь

Плоские линии, прямоугольные координаты точек которых удовлетворяют алгебраическому уравнению 2 й степени. Среди линий второго порядка эллипсы (в частности, окружности), гиперболы, параболы. * * * ЛИНИИ ВТОРОГО ПОРЯДКА ЛИНИИ ВТОРОГО ПОРЯДКА,… … Энциклопедический словарь

Плоские линии, прямоуг. координаты точек к рых удовлетворяют алгебр. ур нию 2 й степени. Среди Л. в. п. эллипсы (в частности, окружности), гиперболы, параболы … Естествознание. Энциклопедический словарь

Плоская линия, декартовы прямоугольные координаты к рой удовлетворяют алгебраич. уравнению 2 й степени Уравнение (*) может и не определять действительного геометрич. образа, но для сохранения общности в таких случаях говорят, что оно определяет… … Математическая энциклопедия

Множество точек 3 мерного действительного (или комплексноро) пространства, координаты к рых в декартовой системе удовлетворяют алгебраич. уравнению 2 й степени (*) Уравнение (*) может и не определять действительного геометрич. образа, в таких… … Математическая энциклопедия

Слово это, весьма часто употребляемое в геометрии кривых линий, имеет не вполне определенное значение. Когда это слово применяется к незамкнутым и неразветвляющимся кривым линиям, то под ветвью кривой подразумевается каждая непрерывная отдельная… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Линии второго порядка, два диаметра, каждый из которых делит пополам хорды этой кривой, параллельные другому. С. д. играют важную роль в общей теории линий второго порядка. При параллельном проектировании эллипса в окружность его С. д.… …

Линии, которые получаются сечением прямого кругового Конуса плоскостями, не проходящими через его вершину. К. с. могут быть трёх типов: 1) секущая плоскость пересекает все образующие конуса в точках одной его полости; линия… … Большая советская энциклопедия

Линии, к рые получаются сечением прямого кругового конуса плоскостями, не проходящими через его вершину. К. с. могут быть трех типов: 1) секущая плоскость пересекает все образующие конуса в точках одной его полости (рис., а):линия пересечения… … Математическая энциклопедия

Раздел геометрии. Основными понятиями А. г. являются простейшие геометрические образы (точки, прямые, плоскости, кривые и поверхности второго порядка). Основными средствами исследования в А. г. служат метод координат (см. ниже) и методы… … Большая советская энциклопедия

Книги

• Краткий курс аналитической геометрии , Ефимов Николай Владимирович. Предметом изучения аналитической геометрии являются фигуры, которые в декартовых координатах задаются уравнениями первой степени или второй. На плоскости — это прямые и линии второго порядка.…

Это общепринятый стандартный вид уравнения, когда в считанные секунды становится ясно, какой геометрический объект оно определяет. Кроме того, канонический вид очень удобен для решения многих практических заданий. Так, например, по каноническому уравнению «плоской» прямой , во-первых, сразу понятно, что это прямая, а во-вторых – элементарно просматривается принадлежащая ей точка и направляющий вектор .

Очевидно, что любая линия 1-го порядка представляет собой прямую. На втором же этаже нас ждёт уже не вахтёр, а гораздо более разнообразная компания из девяти статуй:

Классификация линий второго порядка

С помощью специального комплекса действий любое уравнение линии второго порядка приводится к одному из следующих видов:

( и – положительные действительные числа)

1) – каноническое уравнение эллипса;

2) – каноническое уравнение гиперболы;

3) – каноническое уравнение параболы;

4) – мнимый эллипс;

5) – пара пересекающихся прямых;

6) – пара мнимых пересекающихся прямых (с единственной действительной точкой пересечения в начале координат);

7) – пара параллельных прямых;

8) – пара мнимых параллельных прямых;

9) – пара совпавших прямых.

У ряда читателей может сложиться впечатление неполноты списка. Например, в пункте №7 уравнение задаёт пару прямых , параллельных оси , и возникает вопрос: а где же уравнение , определяющее прямые , параллельные оси ординат? Ответ: оно не считается каноническим . Прямые представляют собой тот же самый стандартный случай , повёрнутый на 90 градусов, и дополнительная запись в классификации избыточна, поскольку не несёт ничего принципиально нового.

Таким образом, существует девять и только девять различных видов линий 2-го порядка, но на практике наиболее часто встречаются эллипс, гипербола и парабола .

Сначала рассмотрим эллипс. Как обычно, я акцентирую внимание на тех моментах, которые имеют большое значение для решения задач, и если вам необходим подробный вывод формул, доказательства теорем, пожалуйста, обратитесь, например, к учебнику Базылева/Атанасяна либо Александрова..

Эллипс и его каноническое уравнение

Правописание… пожалуйста, не повторяйте ошибок некоторых пользователей Яндекса, которых интересует «как построить эллибз», «отличие элипса от овала» и «эксцентриситет элебса».

Каноническое уравнение эллипса имеет вид , где – положительные действительные числа, причём . Само определение эллипса я сформулирую позже, а пока самое время отдохнуть от говорильни и решить распространённую задачу:

Как построить эллипс?

Да, вот взять его и просто начертить. Задание встречается часто, и значительная часть студентов не совсем грамотно справляются с чертежом:

Построить эллипс, заданный уравнением

Решение : сначала приведём уравнение к каноническому виду:

Зачем приводить? Одно из преимуществ канонического уравнения заключается в том, что оно позволяет моментально определить вершины эллипса , которые находятся в точках . Легко заметить, что координаты каждой из этих точек удовлетворяют уравнению .

В данном случае :

Отрезок называют большой осью эллипса;
отрезок – малой осью ;
число называют большой полуосью эллипса;
число – малой полуосью .
в нашем примере: .

Чтобы быстро представить, как выглядит тот или иной эллипс достаточно посмотреть на значения «а» и «бэ» его канонического уравнения.

Всё ладно, складно и красиво, но есть один нюанс: я выполнил чертёж с помощью программы. И вы можете выполнить чертёж с помощью какого-либо приложения. Однако в суровой действительности на столе лежит клетчатый листок бумаги, и на наших руках водят хороводы мыши. Люди с художественным талантом, конечно, могут поспорить, но мыши есть и у вас тоже (правда, поменьше). Таки не зря человечество изобрело линейку, циркуль, транспортир и другие нехитрые приспособления для черчения.

По этой причине нам вряд ли удастся аккуратно начертить эллипс, зная одни вершины. Ещё куда ни шло, если эллипс небольшой, например, с полуосями . Как вариант, можно уменьшить масштаб и, соответственно, размеры чертежа. Но в общем случае крайне желательно найти дополнительные точки.

Существует два подхода к построению эллипса – геометрический и алгебраический. Построение с помощью циркуля и линейки мне не нравится по причине не самого короткого алгоритма и существенной загроможденности чертежа. В случае крайней необходимости, пожалуйста, обратитесь к учебнику, а в реальности же гораздо рациональнее воспользоваться средствами алгебры. Из уравнения эллипса на черновике быстренько выражаем:

Далее уравнение распадается на две функции:
– определяет верхнюю дугу эллипса;
– определяет нижнюю дугу эллипса.

Любой эллипс симметричен относительно координатных осей, а также относительно начала координат . И это отлично – симметрия почти всегда предвестник халявы. Очевидно, что достаточно разобраться с 1-ой координатной четвертью, поэтому нам потребуется функция . Напрашивается нахождение дополнительных точек с абсциссами . Настукаем три смс-ки на калькуляторе:

Безусловно, приятно и то, что если допущена серьёзная ошибка в вычислениях, то это сразу выяснится в ходе построения.

Отметим на чертеже точки (красный цвет), симметричные точки на остальных дугах (синий цвет) и аккуратно соединим линией всю компанию:

Первоначальный набросок лучше прочертить тонко-тонко, и только потом придать нажим карандашу. В результате должен получиться вполне достойный эллипс. Кстати, не желаете ли узнать, что это за кривая?

Мы сейчас покажем, что аффинная классификация кривых второго порядка дается самими наименованиями кривых, т. е. что аффинными классами кривых второго порядка являются классы:

пар действительных пересекающихся прямых;

пар мнимых (сопряженных) пересекающихся;

пар параллельных действительных прямых;

пар параллельных мнимых сопряженных прямых;

пар совпадающих действительных прямых.

Надо доказать два утверждения:

А. Все кривые одного наименования (т. е. все эллипсы, все гиперболы и т. д.) аффинно эквивалентны между собою.

Б. Две кривые различных наименований никогда не являются аффинно эквивалентными.

Доказываем утверждение А. В главе XV, § 3, уже было доказано, что все эллипсы аффинно эквивалентны одному из них, а именно окружности а все гиперболы — гиперболе Значит, все эллипсы, соответственно все гиперболы, аффинно эквивалентны между собою. Все мнимые эллипсы, будучи аффинно эквивалентны окружности — — 1 радиуса также аффинно эквивалентны между собою.

Докажем аффинную эквивалентность всех парабол. Мы докажем даже больше, а именно что все параболы подобны между собою. Достаточно доказать, что парабола, данная в некоторой системе координат своим каноническим уравнением

Для этого подвергнем плоскость преобразованию подобия с коэффициентом — :

Тогда так что при нашем преобразовании кривая

переходит в кривую

что и требовалось доказать.

Переходим к распадающимся кривым. В § формулы (9) и (11), стр. 401 и 402) было доказано, что кривая, распадающаяся на пару пересекающихся прямых, в некоторой (даже прямоугольной) системе координат имеет уравнение

Делая дополнительное преобразование координат

видим, что всякая кривая, распадающаяся на пару пересекающихся действительных, соответственно мнимых сопряженных, прямых, имеет в некоторой аффинной системе координат уравнение

Что касается кривых, распадающихся на пару параллельных прямых, то каждая из них может быть (даже в некоторой прямоугольной системе координат) задана уравнением

для действительных, соответственно

для мнимых, прямых. Преобразование координат позволяет в этих уравнениях положить (или для совпадающих прямых Отсюда следует аффинная эквивалентность всех распадающихся кривых второго порядка, имеющих одно и то же наименование.

Переходим к доказательству утверждения Б.

Заметим прежде всего: при аффинном преобразовании плоскости порядок алгебраической кривой остается неизменным. Далее: всякая распадающаяся кривая второго порядка есть пара прямых, а при аффинном преобразовании прямая переходит в прямую, пара пересекающихся прямых переходит в пару пересекающихся, а пара параллельных — в пару параллельных; кроме того, действительные прямые переходят в действительные, а мнимые — в мнимые. Это вытекает из того, что все коэффициенты в формулах (3) (гл. XI, § 3), определяющих аффинное преобразование, суть действительные числа.

Из сказанного следует, что линия, аффинно эквивалентная данной распадающейся кривой второго порядка, есть распадающаяся кривая того же наименования.

Переходим к нераспадающимся кривым. Опять-таки при аффинном преобразовании действительная кривая не может перейти в мнимую, и обратно. Поэтому класс мнимых эллипсов аффинно инвариантен.

Рассмотрим классы действительных нераспадающихся кривых: эллипсов, гипербол, парабол.

Среди всех кривых второго порядка всякий эллипс, и только эллипс, лежит в некотором прямоугольнике, тогда как параболы и гиперболы (равно как и все распадающиеся кривые) простираются в бесконечность.

При аффинном преобразовании прямоугольник ABCD, содержащий данный эллипс, перейдет в параллелограмм, содержащий преобразованную кривую, которая, таким образом, не может уходить в бесконечность и, следовательно, является эллипсом.

Итак, кривая, аффинно эквивалентная эллипсу, есть непременно эллипс. Из доказанного следует, что кривая, аффинно эквивалентная гиперболе или параболе, не может быть эллипсом (а также, как мы знаем, не может быть и распадающейся кривой. Поэтому остается лишь доказать, что при аффинном преобразовании плоскости гипербола не может перейти в параболу, и наоборот. Это, пожалуй, проще всего следует из того, что у параболы нет центра симметрии, а у гиперболы он есть. Но так как отсутствие центра симметрии у параболы будет доказано лишь в следующей главе, то мы сейчас дадим второе, тоже очень простое доказательство аффинной неэквивалентности гиперболы и параболы.

Лемма. Если парабола имеет общие точки с каждой из двух полуплоскостей, определяемых в плоскости данной прямой d, то она имеет хотя бы одну общую точку и с прямой .

В самом деле, мы видели, что существует такая система координат, в которой данная парабола имеет уравнение

Пусть относительно этой системы координат прямая d имеет уравнение

По предположению на параболе имеются две точки из которых одна, положим лежит в положительной, а другая, — в отрицательной полуплоскости относительно уравнения (1). Поэтому, помня, что можем написать

Понравилось?

Нажмите на кнопку, если статья Вам понравилась, это поможет нам развивать проект. Спасибо!