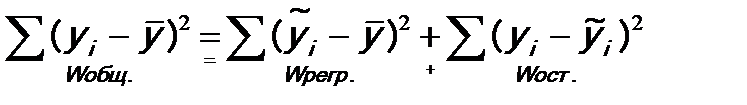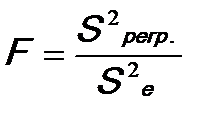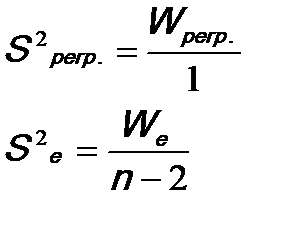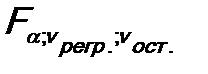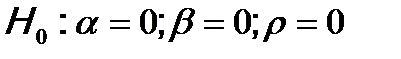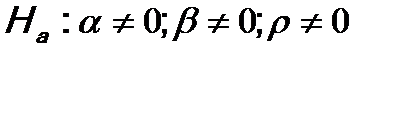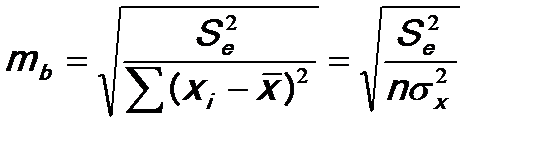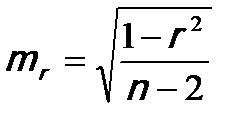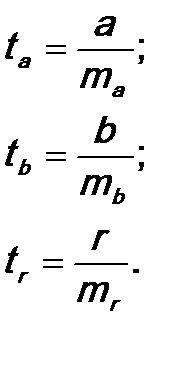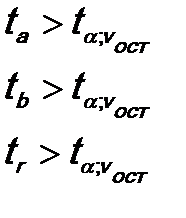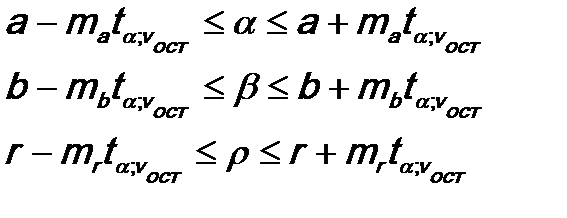5. 1. Точечные оценки коэффициентов регрессии
В некотором эксперименте измерены значения пары случайных величин y и x
Без ограничения общности можно считать, что величина x измерена точно, в то время как измерение величины y содержит случайные погрешности.
Это означает, что погрешность измерения величины x пренебрежимо мала по сравнению с погрешностью измерения величины y. Таким образом, результаты эксперимента можно рассматривать как выборочные значения случайной величины h (x), зависящей от x как от параметра.
Пусть требуется построить зависимость y(x).
Регрессией называют зависимость условного математического ожидания величины h (x) от x:

Задача регрессионного анализа состоит в восстановлении функциональной зависимости y(x) по результатам измерений <(xi,yi)>, i = 1, 2, …, n.
Это означает, что результаты измерений можно представить в виде
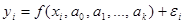
где a0, a1, …, ak — неизвестные параметры регрессии, а e i — случайные величины, характеризующие погрешности эксперимента.
Обычно предполагается, что e i — это независимые нормально распределенные случайные величины с M( e i) = 0 и одинаковыми дисперсиями D( e i) = s 2 .
Параметры a0, a1, …, ak следует выбирать таким образом, чтобы отклонение значений предложенной функции от результатов эксперимента было минимальным. В качестве меры отклонения выберем величину
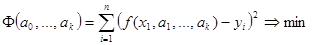
Рассмотрим простейший случай линейной регрессии.
Оценки параметров a и b находим из необходимого условия минимума функции 
приравняв нулю частные производные функции 

получаем точечные оценки параметров (коэффициентов) регрессииa и b:
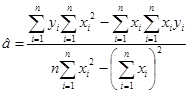
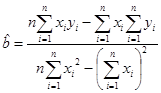
Здесь использованы принятые для точечных оценок обозначения 
Оценка параметров уравнения регреcсии. Пример
Задание:
По группе предприятий, выпускающих один и тот же вид продукции, рассматриваются функции издержек:
y = α + βx;
y = α x β ;
y = α β x ;
y = α + β / x;
где y – затраты на производство, тыс. д. е.
x – выпуск продукции, тыс. ед.
Требуется:
1. Построить уравнения парной регрессии y от x :
- линейное;
- степенное;
- показательное;
- равносторонней гиперболы.
2. Рассчитать линейный коэффициент парной корреляции и коэффициент детерминации. Сделать выводы.
3. Оценить статистическую значимость уравнения регрессии в целом.
4. Оценить статистическую значимость параметров регрессии и корреляции.
5. Выполнить прогноз затрат на производство при прогнозном выпуске продукции, составляющем 195 % от среднего уровня.
6. Оценить точность прогноза, рассчитать ошибку прогноза и его доверительный интервал.
7. Оценить модель через среднюю ошибку аппроксимации.
1. Уравнение имеет вид y = α + βx
1. Параметры уравнения регрессии.
Средние значения
Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии
Коэффициент детерминации
R 2 =0.94 2 = 0.89, т.е. в 88.9774 % случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая
| x | y | x 2 | y 2 | x ∙ y | y(x) | (y- y ) 2 | (y-y(x)) 2 | (x-x p ) 2 |
| 78 | 133 | 6084 | 17689 | 10374 | 142.16 | 115.98 | 83.83 | 1 |
| 82 | 148 | 6724 | 21904 | 12136 | 148.61 | 17.9 | 0.37 | 9 |
| 87 | 134 | 7569 | 17956 | 11658 | 156.68 | 95.44 | 514.26 | 64 |
| 79 | 154 | 6241 | 23716 | 12166 | 143.77 | 104.67 | 104.67 | 0 |
| 89 | 162 | 7921 | 26244 | 14418 | 159.9 | 332.36 | 4.39 | 100 |
| 106 | 195 | 11236 | 38025 | 20670 | 187.33 | 2624.59 | 58.76 | 729 |
| 67 | 139 | 4489 | 19321 | 9313 | 124.41 | 22.75 | 212.95 | 144 |
| 88 | 158 | 7744 | 24964 | 13904 | 158.29 | 202.51 | 0.08 | 81 |
| 73 | 152 | 5329 | 23104 | 11096 | 134.09 | 67.75 | 320.84 | 36 |
| 87 | 162 | 7569 | 26244 | 14094 | 156.68 | 332.36 | 28.33 | 64 |
| 76 | 159 | 5776 | 25281 | 12084 | 138.93 | 231.98 | 402.86 | 9 |
| 115 | 173 | 13225 | 29929 | 19895 | 201.86 | 854.44 | 832.66 | 1296 |
| 0 | 0 | 0 | 16.3 | 20669.59 | 265.73 | 6241 | ||
| 1027 | 1869 | 89907 | 294377 | 161808 | 1869 | 25672.31 | 2829.74 | 8774 |
Примечание: значения y(x) находятся из полученного уравнения регрессии:
y(1) = 4.01*1 + 99.18 = 103.19
y(2) = 4.01*2 + 99.18 = 107.2
. . .
2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;α/2) = (11;0.05/2) = 1.796
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.
Анализ точности определения оценок коэффициентов регрессии
S a = 0.1712
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-20.41;56.24)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается
Статистическая значимость коэффициента регрессии b не подтверждается
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими (tтабл=1.796):
(a — tтабл·Sa; a + tтабл·S a)
(1.306;1.921)
(b — tтабл·S b; b + tтабл·Sb)
(-9.2733;41.876)
где t = 1.796
2) F-статистики
Fkp = 4.84
Поскольку F > Fkp, то коэффициент детерминации статистически значим
Точечная и интервальная оценка параметров генерального уравнения регрессии
Проверить достоверность уравнения регрессии – значит, установить: соответствует ли математическая модель, выражающая зависимость между переменными связям в генеральной совокупности и достаточно ли включенных в уравнение объясняющих переменных для описания зависимой переменной.
Проверка достоверности уравнения в целом проводится на основе дисперсионного анализа по критерию F-Фишера.
Схема дисперсионного анализа:
1. Выдвигается рабочая гипотеза о равенстве генеральных дисперсий: дисперсии, воспроизведенной (σ 2 регр.) уравнением регрессии, и остаточной дисперсии (σ 2 ост.), а также альтернативная ей:
2. Выбирается уровень значимости критерия 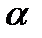
3. Производится разложение общего объема вариации:
Поскольку остатки определяются как:

т.е. отклонения от линии регрессии по каждому наблюдению, будем обозначать остаточный объем вариации как 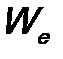
3. Определяется число степеней свободы, которое обозначается d.f. или v:
vобщ.=n-1, где n – численность выборки;
vрегр.=m (m – число параметров без условного начала). Для парной линейной регрессии vрегр.=1
4. Рассчитываются выборочные несмещенные оценки дисперсий:
5. Определяется фактическое значение F-критерия Фишера:
6. Определяется критическое (табличное) значение критерия:
6. Делается статистический вывод:
7. Делается заключение о значимости уравнения в целом, в случае принятия альтернативной гипотезы при выбранном уровне вероятности суждения 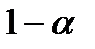
Если уравнение регрессии в целом значимо, то имеет смысл оценить значимость его параметров по t-критерию Стьюдента. Этот критерий применяется также для оценки значимости коэффициента парной корреляции, поскольку r – это лишь выборочная оценка генерального коэффициента корреляции 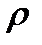
Схема t-теста:
1. Формулируются рабочая и альтернативная гипотезы:
2. Выбирается уровень значимости критерия 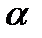
3. Рассчитываются средние ошибки выборочных характеристик:
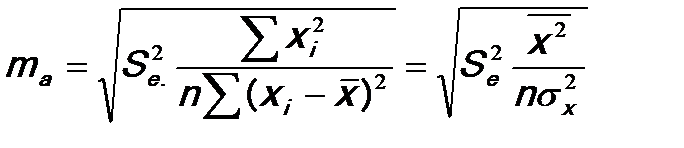
где 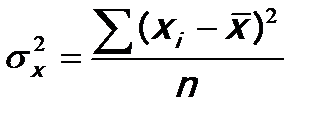
4. Определяются фактические значения t-критерия:
5. Определяется критическое значение:
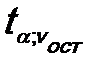
6. Фактические значения сравниваются с критическими. Тестируемые параметры будут значимыми, если:
Отметим, что в парной линейной модели, поскольку в модели всего один регрессор:
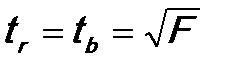
Если параметры уравнения оказались значимыми, то возможна их интерпретация и распространение выводов на генеральную совокупность.
В этом случае возможна их интервальная оценка:
Нужно иметь ввиду, что существенные параметры регрессии не могут менять знаки на противоположные. Если нижняя граница у Вас получается отрицательной, а выборочный параметр при этом – положительный, то в качестве нижней границы следует взять ноль. Аналогично для коэффициента корреляции, к тому же нужно помнить, что он изменяется в пределах от -1 до 1, соответственно предельные границы в генеральной совокупности не могут превышать по модулю единицу.
http://math.semestr.ru/corel/prim4.php
http://poisk-ru.ru/s63663t1.html