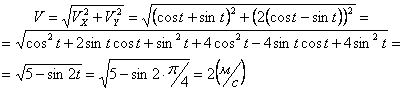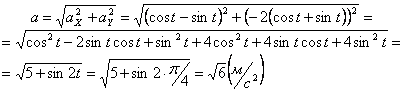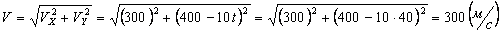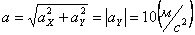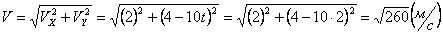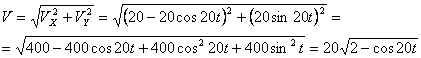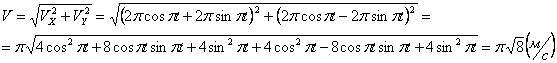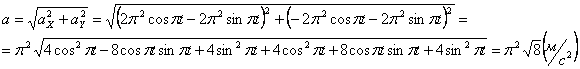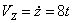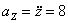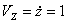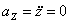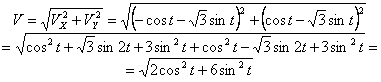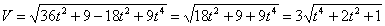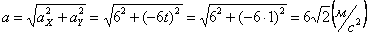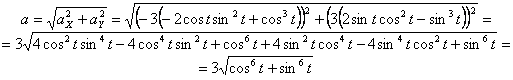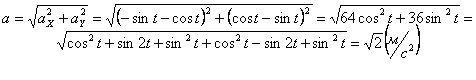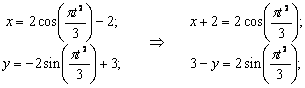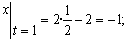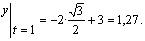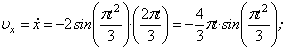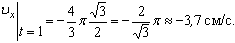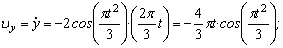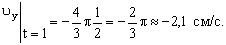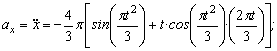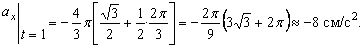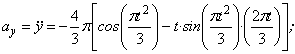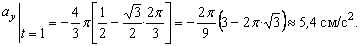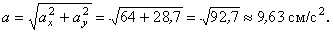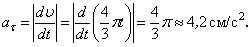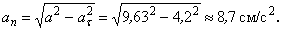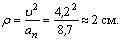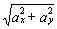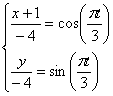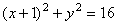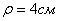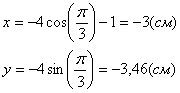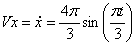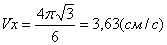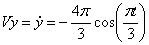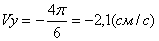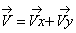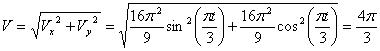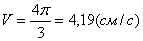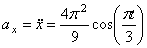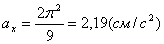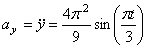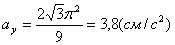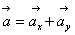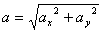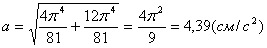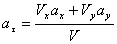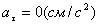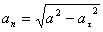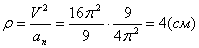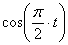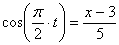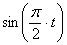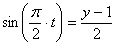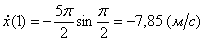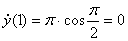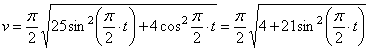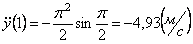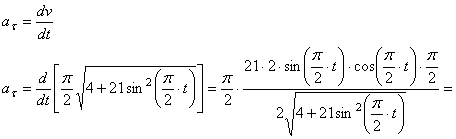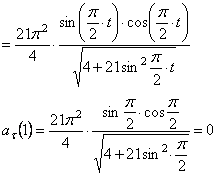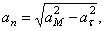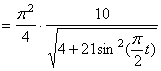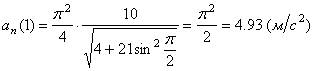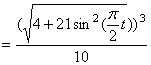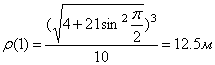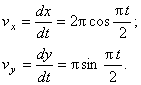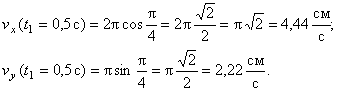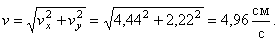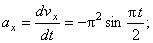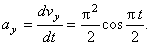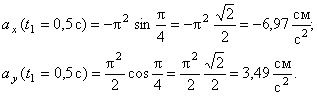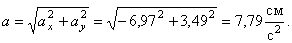Точка а движется согласно уравнениям x1

Точка а движется согласно уравнениям x1

скорость точки момент времени

Материальная точка массой m = 5 г совершает гармонические колебания с частотой ν = 0,5 Гц. Амплитуда колебаний А = 3 см. Определить; 1) скорость v точки в момент времени, когда смещение х = 1,5 см; 2) максимальную силу F_max, действующую на точку; 3) полную энергию E колеблющейся точки.

Материальная точка начинает двигаться по окружности с угловым ускорением ε = k·t, где k = 4 рад/с 3 . Определить угловую скорость точки в момент времени t₁ = 2 c.

Движения двух материальных точек выражаются уравнениями: x₁ = A₁+B₁t+C₁t 2 , x₂ = A₂+B₂t+C₂t 2 , где A₁ = 20 м, A₂ = 2 м, B₁ = B₂ = 2 м/с, C₁ = 4 м/с 2 , С₂ = 0,5 м/с 2 . В какой момент времени t скорости этих точек будут одинаковыми? Определить скорости v₁ и v₂ и ускорения a₁ и а₂ точек в этот момент.

Материальная точка массой т = 900 кг движется по горизонтальной прямой под действием силы F = 270t, которая направлена по той же прямой. Определить скорость точки в момент времени t = 10 с, если при t₀ = 0 скорость ν₀ = 10 м/с.

Точка движется по траектории согласно уравнению s = 0,5t 2 + 4t. Определить, в какой момент времени скорость точки достигнет 10 м/с.

По прямой линии движутся две материальные точки согласно уравнениям: х₁ = 10 + t + 2t 2 и x₂ = 3 + 2t + 0,2t 2 . В какой момент времени скорости этих точек одинаковы?

Две материальные точки движутся согласно уравнениям x₁ = A₁t + B₁t 2 + C₁t 3 и x₂ = A₂t + B₂t 2 + C₂t 3 , где A₁ = 2 м/с; B₁ = –4 м/с 2 ; C₁ = 1 м/с 3 ; A₂ = 4 м/с; B₂ = 8 м/с 2 ; C₂ = –16 м/с 3 . В какой момент времени скорости этих точек будут одинаковы? Найти ускорения точек в этот момент времени.

Точка движется по прямой согласно уравнению x = At – Bt 3 – С, где А = 4 м/с, В = 3 м/с 3 , С = 1 м. Найти координаты х точки в моменты времени, когда скорость v равна нулю.

Материальная точка на плоскости совершает движение, которое задается кинематическими уравнениями: х = A·cos(ω·t); у = B·cos(ω·t + φ₀), где х и у — координаты точки в момент времени t, А = 4 м, В = 8 м, φ₀ = π, ω = π рад/с. Определить траекторию точки и скорость точки в момент времени t₁ = 1 с.

Движения двух материальных точек задаются уравнениями v₁(t) = B₁t + C₁t 2 , х₂(t) = B₂t 2 + C₂t 3 , где B₁ = 8 м/с, B₂ = 2 м/с 2 , С₁ = 4 м/с 2 , С₂ = 5 м/с 3 . Определить скорости v₁ и v₂, ускорения а₁ и а₂ точек в момент времени когда их скорости будут одинаковыми.

Движение точки задано уравнениями x = A₁sinωt и y = A₂sinω(t+τ), где А₁ = 10 см, А₂ = 5 см, ω = 2 рад/с, τ = π/4 с. Найти уравнение траектории и скорости точки в момент времени t = 0,5 с.

Движение материальной точки задано уравнением: x = A+Bt 2 , где А = 4 м/с, В = –0,05 м/с 2 . Определить момент времени, в который скорость точки v = 0. Найти координату и ускорение точки в этот момент.

Две материальные точки движутся вдоль одной прямой с ускорениями a₁ = A₁+B₁t, a₂ = A₂+B₂t, где A₁ = 4 м/c 2 , B₁ = 3 м/с 3 , A₂ = 12 м/с 2 , B₂ = –1 м/с 3 . Начальные скорости этих точек были равны, соответственно, 8 м/с и 12,5 м/с. В какой момент времени t скорости точек будут одинаковы?

Материальная точка массой m = 5 кг в начале движения по горизонтальной прямой малая скорость V₀ = 3 м/с и на нее действовала сила F = 8 + 3t, которая направлена по той же прямой. Определить скорость точки в момент времени t₁ = 4 с.

Определение сил по заданному движению

ДИНАМИКА ТОЧКИ

Определение сил по заданному движению

13.1.1Точка массой m=4 кгдвижется по горизонтальной прямой с ускорениемa=0,3t. Определить модуль силы, действующей на точку в направлении ее движения в момент времени t=3c. (3.6) Решение:Зная массу и ее ускорение, можно определить действующую на точку силу, в момент времени t=3c , ускорение будет тогда

13.1.2Ускорение движения точки массой m=27кгпо прямой задано графиком функции a=а(t). Определить модуль равнодействующей сил, приложенных к точке в момент времени t=5c. (4,05) Решение:Из графика видно что при t=5c , ускорение а=0,15м/с 2 , тогда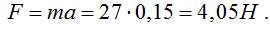

13.1.3 Деталь массой m=0,5кг скользит вниз по лотку. Под каким углом к горизонтальной плоскости должен располагаться лоток, для того чтобы деталь двигалась с ускорением а=2 м/с 2 ? Угол выразить в градусах. (11,8) Решение:Деталь движется под силой тяжести G=mg, сила под которой она движется по лотку с некоторым углом а,

13.1.4Точка массой m=14кгдвижется по горизонтальной оси Ох с ускорениемах.=lnt Определить модуль силы, действующей на точку в направлении движения в момент времени t=5c. (22,5) Решение:

13.1.5Трактор, двигаясь с ускорением а=1м/с 2 по горизонтальному участку пути, перемещает нагруженные сани массой 600кг. Определить силу тяги на крюке, если коэффициент трения скольжения саней f=0,04. (835) Решение:Необходимая сила тяги на крюке для перемещения саней с заданным ускорением 1м/с 2 :

13.1.6Тело массой m=50 кг, подвешенное на тросе, поднимается вертикально с ускорением а=0,5м/с 2 . Определить силу натяжения троса.(516) Решение:

13.1.7 Скорость движения точки m=24кг по прямой задана графиком функцииv=v(t). Определить модуль равнодействующей сил, действующих на точку. (36) Решение: из графика функции v=v(t) видно, что точка движется равноускоренно с ускорением а=1,5м/с, тогда равнодействующая сил

13.1.8 Материальная точка массой m=12кгдвижется по прямой со скоростьюv=е 0,1t . Определить модуль равнодействующей сил, действующих на точку в момент времени t=50c.(178) Решение:

13.1.9 Определить модуль равнодействующей сил, действующих на материльную точку массой m=3кг в момент времени t=6c, если она движется по оси Ох согласно уравнению х=0,04t 3 . (4,32) Решение:Ускорение точки найдем из уравнения движения (вторая производная по времени):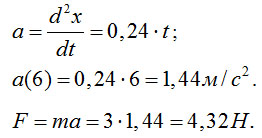

13.1.10 Материальная точка массой 1,4кг движется прямолинейно по законух=6t 2 +6t+3 . Определить модуль равнодействующей сил, приложенных к точке.(16,8) Решение:

Определение сил по заданному движению

Точка а движется согласно уравнениям x1

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ

7.1. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .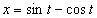

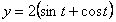
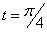
Решение: Скорости точки :

,

,

,

,

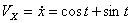
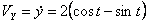
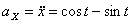
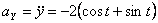
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

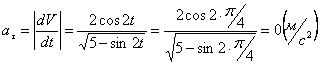
А модуль нормального ускорения:

.

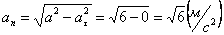
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

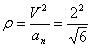
7.2. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .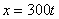

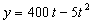
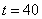
Решение: Скорости точки :

,

,

,

,

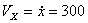
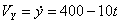
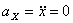
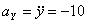
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

А модуль нормального ускорения:

.

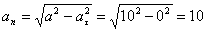
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

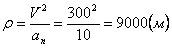
7.3. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .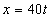

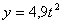
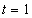
Решение: Скорости точки:

,

,

.

,

,

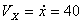
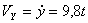
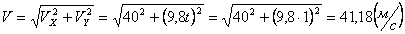
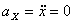
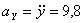
Модуль полного ускорения:

.

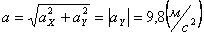
Модуль касательного ускорения точки:

,

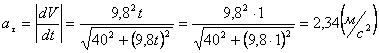
А модуль нормального ускорения:

.

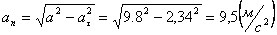
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

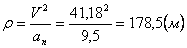
7.4. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .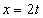

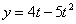
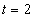
Решение: Скорости точки :

,

,

,

,

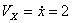
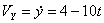
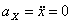
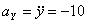
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

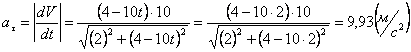
А модуль нормального ускорения:

.

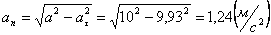
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

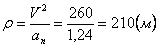
7.5. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .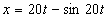

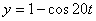
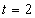
Решение: Скорости точки по осям :

,

,

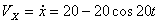
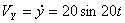
Ускорения точки по осям:

,

,

.

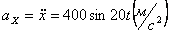
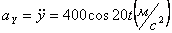
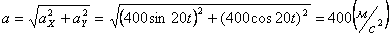
Модуль касательного ускорения точки:

, а модуль нормального ускорения .

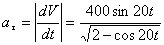
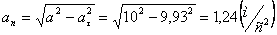
Нормальное ускорение и радиус кривизны траектории связаны соотношением .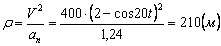

7.6. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .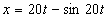

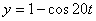
Решение: Скорости точки по осям :

,

,

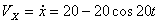
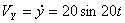
Ускорения точки по осям:

,

,

.

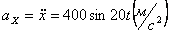
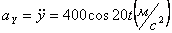
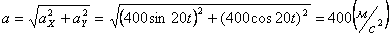
Модуль касательного ускорения точки:

,

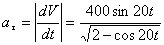
а модуль нормального ускорения:

.

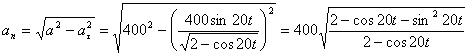
Нормальное ускорение и радиус кривизны траектории связаны соотношением .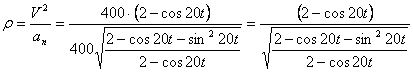

7.7. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .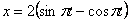

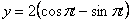
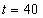
Решение: Скорости точки :

,

,

,

,

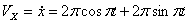
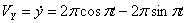
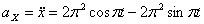
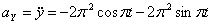
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

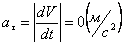
А модуль нормального ускорения:

.

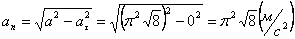
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

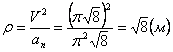
7.8. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .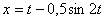

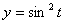
Решение: Скорости точки :

,

,

.

,

,

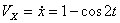
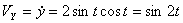
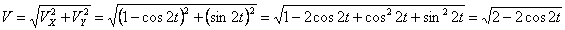
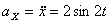
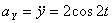
Модуль полного ускорения:

.

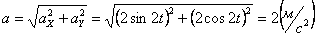
Модуль касательного ускорения точки:

,

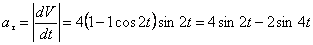
А модуль нормального ускорения:

.

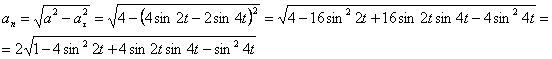
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

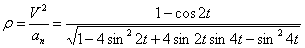
7.9. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , , .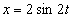

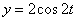
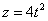
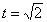
Решение: Скорости точки :

,

,

.

,

,

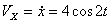
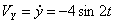
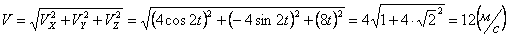
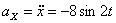
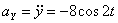
Модуль полного ускорения:

.

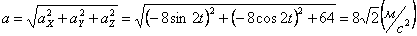
Модуль касательного ускорения точки:

,

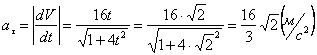
А модуль нормального ускорения:

.

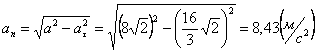
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

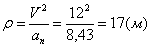
7.10. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .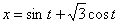

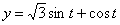
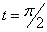
Решение: Скорости точки :

,

,

,

,

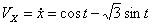
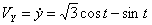
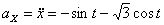
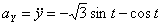
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

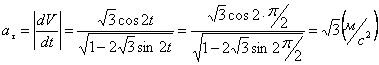
А модуль нормального ускорения:

.

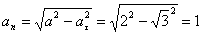
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

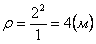
7.11. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .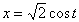

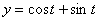
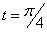
Решение: Скорости точки :

,

,

,

,

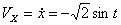
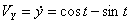
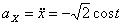
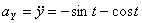
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

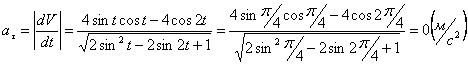
А модуль нормального ускорения:

.

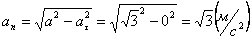
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

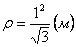
7.12. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , , .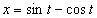

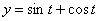
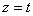
Решение: Скорости точки :

,

,

,

,

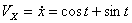
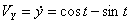
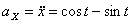
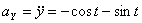
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

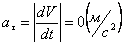
А модуль нормального ускорения:

.

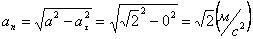
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

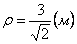
7.13. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .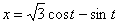

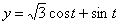
Решение: Скорости точки :

,

,

,

,

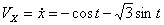
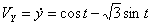
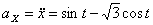
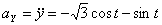
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

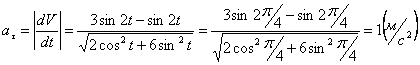
А модуль нормального ускорения:

.

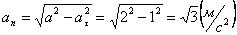
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

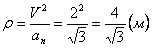
7.14. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .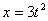

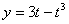
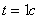
Найти: , , .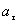

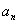
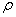
Решение: Скорости точки по осям :

,

,

,

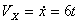
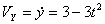
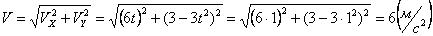
Ускорения точки по осям:

,

,

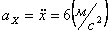
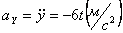
Модуль касательного ускорения точки:

,

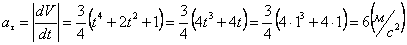
А модуль нормального ускорения:

.

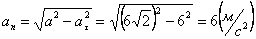
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

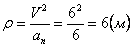
7.15. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .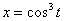

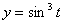
Решение: Скорости точки :

,

,

,

,

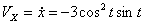
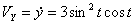
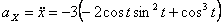
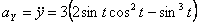
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

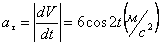
А модуль нормального ускорения:

.

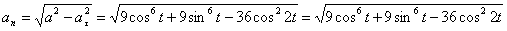
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

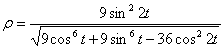
7.16. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .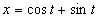

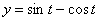
Решение: Скорости точки :

,

,

,

,

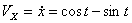
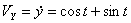
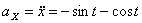
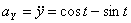
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

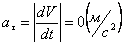
А модуль нормального ускорения:

.

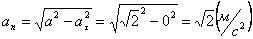
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

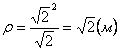
7.17. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .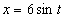

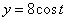
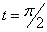
Решение: Скорости точки :

,

,

,

,

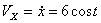
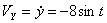
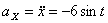
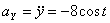
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

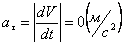
А модуль нормального ускорения:

.

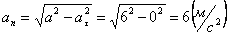
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

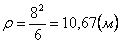
7.18. Дан закон движения точки по окружности радиусом r . Определить:

1) скорость и ускорение точки при 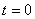и ;

2) моменты остановки точки;

3) путь, пройденный точкой за 10секунд.

Дано: , , , .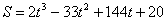

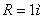
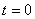
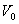
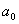
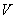
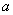
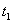
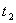
Найти: , , , , , , П.

Решение: 1. На траектории отметим точку О – начало отсчета координаты s и укажем положительное направление отсчета этой координаты. Отметим положение точки в заданные моменты времени: При :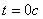

;

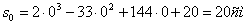
При :

.

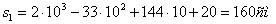
Проведем из этих точек естественные оси координат.

Определим проекцию скорости на касательную:

.

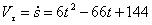
При : ;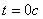

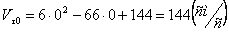
При : .

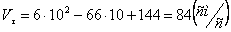
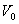
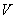
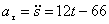
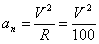
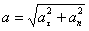
Векторы и совпадают со своими проекциями. Определим проекции ускорения на естественнее оси координат :

; , Полное ускорение точки .

При :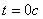

,

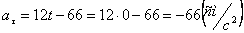
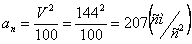
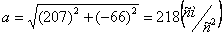
и

.

При :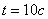

,

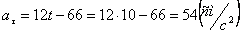
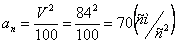
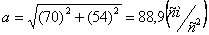
и

.

2. Чтобы найти время остановки надо найти время, когда скорость точки равна нулю:

, получим и .

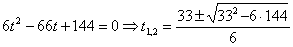
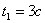
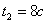
3. Поскольку за 10 секунд точка сделала две остановки, пройденный ею путь за 10с можно найти как сумму пути, пройденного от начала до первой остановки, от первой до второй остановки и от второй до момента времени :

,

; ; ; .

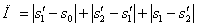
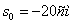
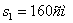
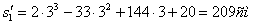
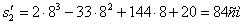
Путь пройденный точкой за 10 секунд:

.

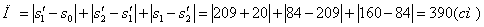
7.19. Определить скорость, касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

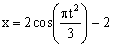
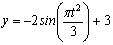
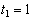
Дано: , (1)

( x и y – в см , t и t ₁ – в с).

Найти: 1) вид траектории;

2) для t = t ₁ положение точки на траектории;

3) .

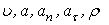
Решение: 1) Уравнение движения (1) можно рассматривать как параметрические уравнения траектории точки. Чтобы получить уравнения траектории в координатной форме, исключаем время t из уравнений (1).

Возводя обе части равенств в квадрат, а затем складывая равенства, получаем 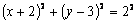, т.е. траекторией точки М является окружность радиуса 2, показанная на рис.1.

2) Определяем положение точки М в заданный момент времени t =1 с :

Вектор скорости точки

. (2)

(3)

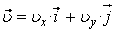
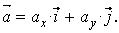
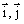
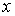
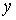
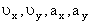
Здесь – орты осей и ; – проекции скорости и ускорения точки на оси координат.

Найдем их, дифференцируя по времени уравнения движения (1):

По найденным проекциям определяем модуль скорости:

, (4)

,

,

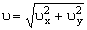
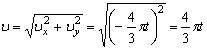
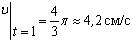
и модуль ускорения точки:

, (5)

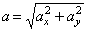
Модуль касательного ускорения точки

, (6)

; (7)

выражает проекцию ускорения точки на направление ее скорости. Знак «+» при означает, что движение точки ускоренное, направление и совпадают; знак «–» – что движение замедленное.

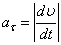
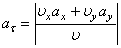
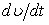
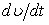
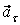
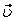
Вычисляем модуль касательного ускорения для заданного момента времени

Модуль нормального ускорения точки

. (8)

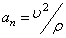
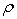
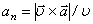
Если радиус кривизны траектории в рассматриваемой точке неизвестен, то нормальное ускорение можно определить по формуле

. (9)

При движении точки в плоскости формула (9) принимает вид

.

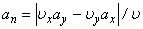
Модуль нормального ускорения можно определить и следующим образом:

. (10)

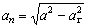
Воспользуемся в нашем случае формулой (10)

Радиус кривизны траектории в рассматриваемой точке определим из выражения:

. (11)

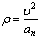
Тогда

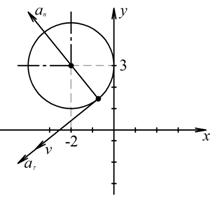
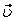
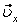
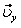
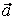
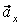
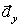
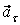
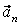
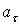
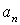
На рис. 1 показано положение точки М в заданный момент времени. Вектор строим по составляющим и , причем этот вектор должен по направлению совпадать с касательной к траектории. Вектор строим по составляющим и и затем раскладываем на составляющие и . Совпадение величин и , найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.

7.20. Определить скорость, касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

( x и y – в см , t и t ₁ – в с).

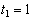
Найти: 1) вид траектории;

2) .

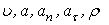
Указания. Задача — относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения. В задаче все искомые величины нужно определить только для момента времени t ₁ = 1 с .

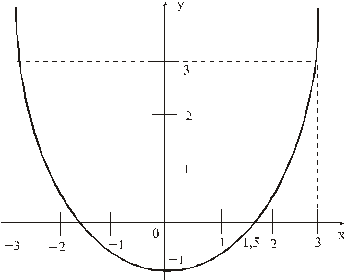
1. Для определения уравнения траектории точки исключим из заданных уравнений движения время t :

Отсюда окончательно находим уравнение траектории точки (параболы, см. рисунок):

2. Скорость точки найдем по ее проекциям на координатные оси:

V = 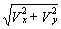и при t ₁ = 1 с,

3. Аналогично найдем ускорение точки:

а =

4. Касательное ускорение найдем, дифференцируя по времени равенство:

. (3)

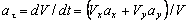
ч исловые значения всех величин, входящих в правую часть выражения (3), определены и даются равенствами (1) и (2).

Подставив в (3) эти числа, найдем сразу, что при t ₁ = 1 с

=7,49 см/с 2 .

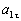
5. Нормальное ускорение точки:

a _n = .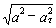

Подставляя сюда найденные числовые значения a ₁ и a _{1 τ} , получим, что при t ₁= 1 с

6. Радиус кривизны траектории ρ = V 2 / a _n .

Подставляя сюда числовые значения V ₁ и a _{1 n} , найдем, что при t ₁ = 1 с

Ответ: V ₁= 8 ,54 см/с, а ₁ =8 см/с 2 , 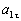=7,49 см/с 2 , a _{1 n} =2,81 см/с 2 , ρ₁ =25,95 см.

7.21. Точка движется по дуге окружности радиуса R =1 м по закону 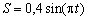( s – в метрах, t – в секундах), где s = AM (см. рисунок).

Найти: скорость и ускорение точки в момент времени t ₁ =1 с .

Определяем скорость точки:

V = ds / dt = .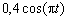

При t ₁ =1 с получим 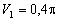= -1,26 м/ с .

Ускорение находим по его касательной и нормальной составляющим:

,

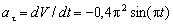
п ри t ₁ = 1 с получим , учтя, что R = 1 м

,

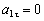
тогда ускорение точки при t ₁ =1 с будет:

=1,59 м/с 2 .

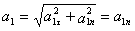
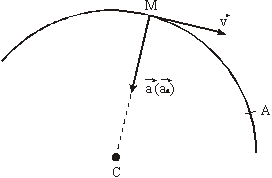
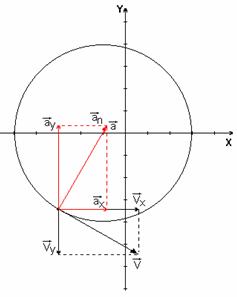
Изобразим на рисунке векторы 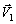, , учитывая знак V ₁ и считая положительным направление от А к М.

7.22. По заданным уравнениям движения точки М установить вид её траектории и для момента времени t = t ₁(с) найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а так же радиус кривизны траектории.

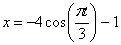
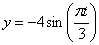
Дано: , , t ₁=1 сек ( x и y – в см , t и t ₁ – в с).

Найти: 1) вид траектории;

2) .

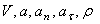
1) Найдём траекторию движения:

Для этого исключим параметр t .

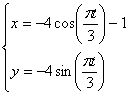
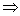
Возведём во вторую степень, получившиеся уравнения, а затем сложим, таким образом, исключится t . Получим:

Это окружность с центром в точке с координатами (-1;0) и радиусом

2) Найдём положение точки на траектории в момент времени t = t _1:

3) Определим скорость токи:

Для нахождения вектора полной скорости необходимо сложить 2 вектора:

Найдём модуль полной скорости:

для момента времени t ₁:

4) Определим ускорение точки:

для момента времени t ₁:

для момента времени t ₁:

Найдём полное ускорение:

Найдём модуль полного ускорения:

для момента времени t ₁:

Определим касательное ускорение :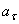

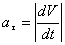
или,

для момента времени t :

Определим нормальное ускорение a_n :

для момента времени t ₁:

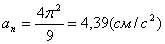
5) Из полученных результатов можно найти радиус кривизны траектории 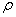, в момент времени t ₁:

Действительно, этот радиус совпадает с радиусом окружности (траектории).

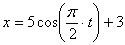
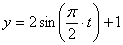
7.23. Точка М движется согласно уравнений ; ; ( x , y — в метрах, t — в секундах). Определить уравнение траектории точки, для момента времени t =1с, найти положение точки, а также скорость, полное, касательное, нормальное ускорения точки и радиус кривизны траектории.

1) Найдем уравнение траектории точки. Для определения уравнения траектории исключим из уравнений движения время . Из первого уравнения движения точки найдем

Из второго уравнения движения найдем

Возведя полученные значения ( правую и левую стороны уравнения ) в квадрат и складывая их находим:

.

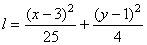
Следовательно, траекторией точки является эллипс с центром в точке с координатами (3;1).

Вид траектории показан на рисунке.

2) Найдем положение точки в момент времени t =1с

; .

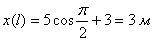
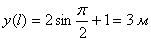
Положение точки М ₁ показано на рисунке.

3) Найдем скорость точки М

,

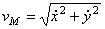
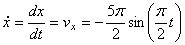
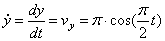
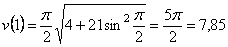
Где , или в момент времени t₁=1c

, или в момент времени t₁=1c

4) Найдём ускорение точки.

,

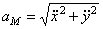
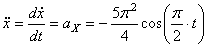
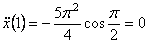
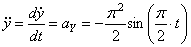
где , или ,

, или

5) Найдем касательное ускорение точки M,

6) Найдём нормальное ускорение точки M ,

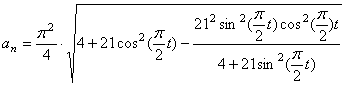
7) Найдем радиус кривизны траектории точки М,

,

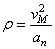
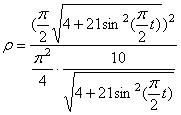
Направление векторов показано на рисунке.

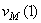
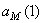
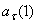
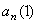
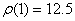
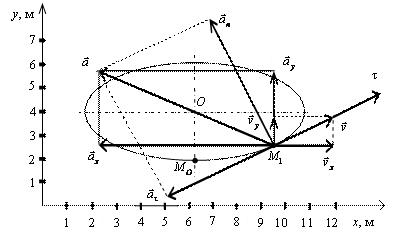
Ответ: =7.85м/ c ; = 4.93 м/ c 2 ; =0; = 4.93 м/ c 2 ; м

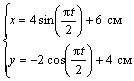
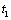
7.24. Пусть точка М движется в плоскости xOy в соответствии с уравнениями . Для момента времени = 0,5 с найти положение точки М на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.

Решение: Заданный закон движения точки в координатной форме можно рассматривать как параметрические уравнения траектории точки. Исключим время t из уравнений движения и получим уравнение траектории точки в виде:

.

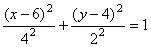
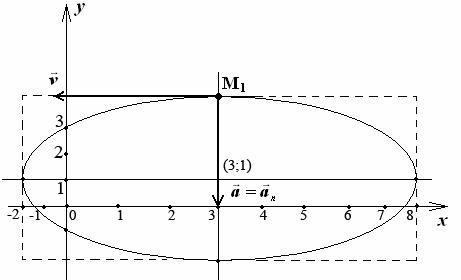
Таким образом, траекторией точки М является эллипс со смещенным центром, изображенный на рис. Отметим на траектории положение точки М ₁ ( x ₁, y ₁) в момент времени t ₁ = 0,5 c

;

.

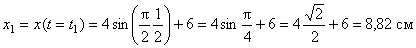
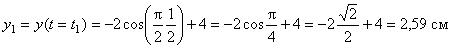
Вектор скорости точки представим в виде:

,

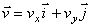
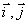
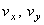
где – орты координатных осей О x и О y ; – проекции вектора скорости точки на координатные оси, которые равны 1-м производным от соответствующих координат по времени

В момент времени t ₁ = 0,5 c

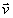
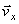
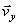
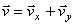
Вектор скорости точки строим по двум взаимно перпендикулярным проекциям и в соответствии с выбранным масштабом

.

Полученный вектор должен быть направлен по касательной к траектории точки в сторону движения. Модуль скорости точки определим по уже найденным проекциям

Вектор ускорения точки представим в виде:

,

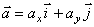
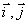
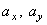
где – орты координатных осей О x и О y ; – проекции вектора скорости точки на координатные оси, которые равны 1-м производным от проекций вектора скорости или 2-м производным от соответствующих координат по времени:

В момент времени t ₁ = 0,5 c

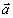
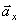
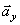
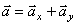
Вектор ускорения точки строим по двум взаимно перпендикулярным проекциям и в соответствии с выбранным масштабом

.

Полученный вектор ускорения точки в общем случае должен отклоняться от вектора скорости в сторону вогнутости траектории, а при движении по эллипсовидной траектории – проходить через центр эллипса. Модуль ускорения точки определим по уже найденным проекциям

Вектор полного ускорения точки можно также представить в виде геометрической суммы его проекций на оси естественной системы отсчета

,

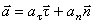
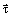
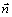
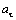
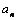
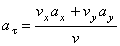
где и – единичные орты касательной и главной нормали; и – соответственно проекции вектора ускорения на касательную и главную нормаль. Касательную М ₁ t направляем по касательной к траектории в сторону движения точки движения, а главную нормаль М₁ n – перпендикулярно касательной в сторону вогнутости траектории. При вычислении касательного ускорения удобно воспользоваться формулой, устанавливающей связь между координатным и естественным способами задания движения точки

.

В момент времени t ₁ = 0,5 c

.

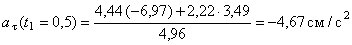
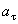
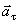
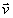
Значение касательного ускорения имеет отрицательный знак, следовательно, в данный момент времени движение точки замедленное и вектор касательного ускорения направлен в противоположную сторону направлению вектора скорости точки .

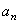
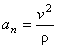
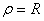
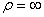
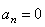
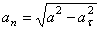
Нормальное ускорение вычислим по формуле , если известен радиус кривизны траектории. Например, если точка движется по окружности радиусом R, то в любой точке траектории . Если же траекторией движения точки является прямая, то , следовательно, . В данном случае радиус кривизны траектории заранее не известен, поэтому нормальное ускорение определяем по формуле:

.

В момент времени t ₁ = 0,5 c

.

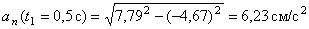
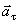
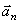
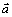
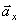
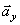
Построим векторы и в соответствии с уже выбранным масштабом, а затем сложим их геометрически. В результате получим тот же вектор полного ускорения точки , который ранее уже был получен геометрической суммой составляющих и . Этот факт служит контролем правильности решения.

Радиус кривизны траектории в рассматриваемой точке определим по формуле

.

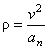
В момент времени t ₁ = 0,5 c

.

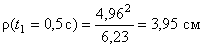
Ответ: 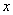=8,82 см; =2,59 см; =4,44 см/ c ; =2,22 см/ c ; =4,96 см/с; =6,97 см/с 2 ; =3,49 см/с 2 ; =7,79 см/с 2 ; =4,67 см/с 2 ; =6,23 см/с 2 ; =3,95 см (радиус кривизны траектории в точке ).

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21