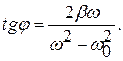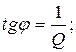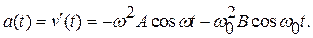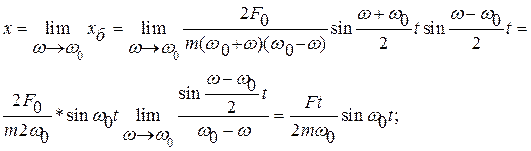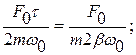Особая точка типа центр
В качестве примера системы, фазовый портрет который содержит особую точку типа центр, рассмотрим гармонический осциллятор. Его динамическое уравнение:
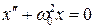
Получим уравнение фазовой траектории. Для этого запишем динамическое уравнение в стандартной форме:
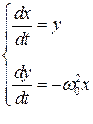
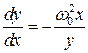
И найдем координаты особой точки
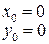
Рассмотрим поведение фазовых траекторий вблизи особой точки. Решим уравнение (3.16) методом разделения переменных:
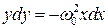
Интегрирую левую и правую части, получим
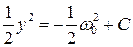
Где 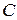
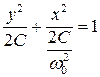

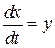
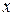
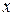
Особая точка, окруженная эллипсами, является частным случаем особой точки типа центр. В общем случае фазовые траектории могут иметь любую форму. Сформулируем определение центра.
Центром называется изолированная особая точка, окруженная замкнутыми траекториями, вложенная друг в друга.
Как уже указывалось, метод фазовой плоскости является качественным методом исследования систем. Воспользуемся тем, что нам известно точное решение уравнения гармонического осциллятора:
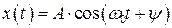
И у нас есть его фазовый портрет. Посмотрим, какую информацию несет фазовый портрет о движении системы
1) Колебание во времени периодическое. На фазовой плоскости это отображается замкнутой траекторией.
2) Форма колебаний гармонического осциллятора – синусоида, на фазовой плоскости траектория – эллипс.
Можно утверждать: если форма колебаний гармоническая, то на фазовой плоскости фазовые траектории – эллипсы; если фазовые траектории отличаются от эллипса, то колебания не гармонические.
3) С помощью фазовой траектории можно оценить амплитуду колебаний 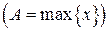
Дата добавления: 2015-01-13 ; просмотров: 2211 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Энергетический подход к нахождению периода колебаний
Рассмотрим механическую систему, положение которой может быть задано с помощью одной величины, которую мы обозначим – х. В таких случаях говорят, что система имеет одну степень свободы. Величиной – х может быть угол отсчитываемый от некоторой плоскости, или расстояние отсчитываемое вдоль заданной кривой (в частности, прямой) линии, и т. п. В этом случае потенциальная энергия системы будет функцией одной переменной – х: U(x).
Рассмотрим одномерное движение частицы массой m в поле, описываемом потенциальной энергией U(x). Динамическое уравнение движения (второй закон Ньютона) для частицы имеет вид
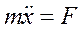
где 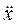
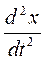
F = — 
Чтобы найти зависимость координаты от времени, надо проинтегрировать уравнение движения, которое является дифференциальным уравнением второго порядка. Однако в случае одномерного движения нет необходимости это делать. Так как потенциальная энергия U(x) не зависит от времени t, то энергия частицы должна сохраняться: E = const. Энергия частицы определяется суммой кинетической и потенциальной энергий
E = 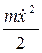
где 
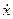
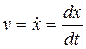
Запишем закон сохранения энергии для пружинного маятника, совершающего колебания в горизонтальной плоскости
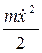

Продифференцировав это выражение по времени, мы получим дифференциальное уравнение гармонических колебаний:
Для электрического колебательного контура без потерь (сопротивление R = 0) закон сохранения энергии можно представить в виде 

где первое слагаемое – энергия накопленная в магнитном поле катушки индуктивности, второе – энергия накопленная в электрическом поле конденсатора.
После дифференцирования по времени L q» + 
Для крутильных колебаний закон сохранения энергии можно представить в виде



где первое слагаемое – кинетическая энергия поворачивающегося тела с моментом инерции J, второе – энергия упругой деформации закрученной нити, на которой подвешено данное тело ( r – коэффициент пропорциональности).
После дифференцирования J α» + r α = 0.
Для физического маятника закон сохранения энергии можно представить в виде




где первое слагаемое — кинетическая энергия поворачивающегося тела с моментом инерции J, второе – потенциальная энергия тела, чей центр масс в результате поворота поднят на высоту h.
Относительно скорости уравнение (94) является дифференциальным уравнением первого порядка, которое можно проинтегрировать путем разделения переменных. Из уравнения (94) скорость частицы
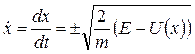
Откуда, разделяя переменные и интегрируя, получим
t — t0 = ± 
Поскольку кинетическая энергия — величина существенно положительная, то при движении полная энергия всегда больше потенциальной, т. е. движение может происходить только в тех областях пространства, где
Одномерное финитное движение является колебательным – частица совершает периодически повторяющееся движение между двумя границами (на рис. 9 в потенциальной яме или АВ между точками х1 и х2). Время между ограничивающими финитное движение точками остановки х1 и х2 одинаково в прямом и обратном направлении. Поэтому период колебаний Т, т. е. время, за которое частица пройдет от х1 до х2 и обратно, равен удвоенному времени прохождения отрезка от х1 до х2, т. е.
T(E) = 2 
Причем приделы интегрирования х1 и х2 являются корнями уравнения (94) при данном значении E. Период колебаний частицы является функцией ее энергии. Вид этой функциональной зависимости определяется видом потенциальной энергии U(x).
Рассмотрим случай малых колебаний, которые система совершает в области своего положения устойчивого равновесия. В положении устойчивого равновесия функция U(x) имеет минимум. Условимся координату х и потенциальную энергию U(x) отсчитывать от положения равновесия. Тогда U(0) = 0.
Разложим функцию U(x) в ряд по степеням х, причем ограничимся рассмотрением малых колебаний, так что высшими степенями х можно будет пренебречь. По формуле Тейлора
U(x) = U(0) + U'(0) · x + 
Ввиду малости х остальными членами пренебрегаем. Они важны в нелинейных процессах.
Так как U(x) при х = 0 имеет минимум, то U'(0) = 0, а вторая производная U»(0) положительна. Кроме того, U(0) = 0. Тогда
U(x) = 
где введено обозначение
Сила, действующая на частицу, в этом случае
F = — 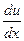
и второй закон Ньютона
m 
Отсюда находим x(t) в виде гармонического колебания, введя обозначение

Добротность
Добротность – очень емкое понятие в теории колебаний. Дело в том, что любая одномерная колебательная система всегда характеризуется двумя основными параметрами: w0 – собственной частотой и b — коэффициентом затухания. Следует отметить, что понятие коэффициента затухания вводится при условии, что сила трения, действующая на осциллятор, пропорционально скорости Fсопр
rV . Если закон сопротивления другой, как, например, при колебаниях с сухим трением, то введение b затруднительно. Пусть указанные два параметра ввести можно; тогда можно ввести и их отношения w0/b0 — мы получим безразмерный параметр, который и называется добротностью. Иногда в частных исследованиях вводят величины, отличающиеся от w0/b на некоторый постоянный множитель. Но это ничего не меняет.
При указанных условиях уравнение колебаний имеет вид
Здесь на осциллятор действует только собственная возвращающая сила Fв= -w0 2 x и сила трения Fт = -2bx’, х(t) – любая колеблющаяся физическая величина: смещение частицы от положения устойчивого равновесия, сила тока в колебательном контуре, смещение столбика газа в акустическом резонаторе и т.д.
Решением уравнения (110) при условии w0 > b является затухающая гармоника (рис. 26)
х(t) = Ае — b t cos (wt + j),
где w 2 = w0 2 — b 2 , а величина а = Ае — b t может рассматриваться как переменная во времени амплитуда. Пусть t — время, за которое амплитуда уменьшается в е раз, т.е.
за это время осциллятор успевает совершить Ne колебаний
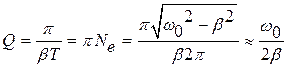
называемый добротностью. Из (104) следует, что добротность в p раз больше числа колебаний, совершаемых за такое время, что амплитуда колебаний уменьшается в е раз.
1. Рассмотрим убыль энергии осциллятора при затухающих колебаниях. Запас механической энергии
E = 
E = 
здесь Е0 – начальный запас энергии в системе. Продифференцируем (101) по времени и определим скорость убыли энергии осциллятора:

Будем считать период колебаний Т достаточно малым, таким, что Т
dt, что оправдано для высокодобротных колебаний, тогда изменение энергии за период DЕ из (101):


Таким образом, добротность осциллятора в 2p раз больше убыли его энергии за период (рис. 24).
2. Рассмотрим вынужденные колебания осциллятора и пусть
внешняя вынуждающая сила F = F0 cos wt будет гармонической. Уравнение вынужденных колебаний возьмем в виде

где f = 
Решение этого уравнения в виде установившихся колебаний (без учета переходного процесса) имеет вид (86 — 87):
х(t)=Аcos(wt+j), A(w) =
Функция А(w) – амплитуда установившихся колебаний, она имеет максимум на резонансной частоте

На этой частоте амплитуда колебаний (резонансная) имеет значение

Эти соотношения уточняют приведенные ранее.
Из (102) находим, что на частоте близкой к нулю
A(0) =
Таким образом, слабая внешняя сила, действующая на осциллятор с частотой wр способна раскачать его до амплитуд тем больших, чем меньше b. Можно утверждать, что слабый сигнал, поступивший в колебательную систему, усиливается, причем коэффициент усиления, понимаемый как отношение амплитуды на резонансной частоте и на низких частотах, равен
K = 
Таким образом, добротность указывает, во сколько раз резонансная амплитуда больше амплитуды установившихся колебаний на низких частотах (рис. 24).
3. Рассмотрим сдвиг фаз между вынуждающей силой и установившимися колебаниями, задаваемый формулой (87). Преобразуем ее к виду
Таким образом, добротность равна котангенсу сдвига фаз на некоторой частоте w3С = 0, 618033988w0 (между вынуждающей силой и установившимися колебаниями)
Установим связь добротности с шириной частотной полосы резонансного контура. Представим схематично этот вывод. Итак, определим частотный диапазон на резонансной кривой, для которого амплитуда вынужденных колебаний в k раз меньше амплитуды в резонансе. Рассмотрим резонанс смещений. Этот диапазон и есть ширина частотной полосы по уровню 1/ k . Имеем
A= f0/( 
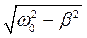
(ω 2 0 – ω 2 ) 2 + 4β 2 ω 2 = 4 β 2 k 2 (ω 2 0 — β 2 ).
Возведем это выражение в квадрат и получим биквадратное уравнение относительно ω :
ω 4 + ω 2 (4 β 2 — 2 ω 2 0 ) + ω 4 0 — 4 β 2 k 2 ω 2 0 +4 β 4 k 2 = 0.
Пусть корни этого уравнения ω1 2 и ω2 2 . Для дальнейшего анализа применим теорему Виетта. Имеем
Членом, содержащим β 4 , мы пренебрегли ввиду его малости.
Составим выражение, содержащее разность частот ω1 и ω2 :
= — 4 β 2 + 2 ω 2 0 — 2 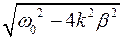
Составим выражение для относительной ширины частотной полосы

Таким образом, относительная ширина частотной полости (по уровню 1/k) Dw/w0 обратно пропорциональна добротности осциллятора. Чем выше добротность, тем острее резонансная кривая (рис. 24).
Рассмотрим процесс установления колебаний на частоте близкой к w0 в осцилляторе, не имеющем затухания (b = 0). Свободные колебания такой осциллятор совершает на частоте w0
а вынужденные — на частоте вынуждающей силы w близкой к w0
Общее решение уравнения (80), учитывающее переходной процесс установления вынужденных колебаний и вынужденное колебание, имеет вид
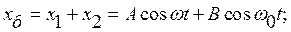
Пусть колебания начинаются из состояния устойчивого равновесия и состояния покоя, но с ускорением, вызванным внешней силой с амплитудой F0. Таким образом
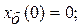


Найдем скорость v (t) и ускорение a(t), продифференцировав (106)
Подставив сюда начальные условия (107), найдем амплитуды A и В (постоянные интегрирования) и получим
B = -A;
Тогда общее решение (80) примет вид
Это выражение представляет собой биения.
Устремим теперь частоту вынуждающей силы w к частоте собственных колебаний осциллятора w0
Таким образом, амплитуда колебаний при раскачке осциллятора в нашем случае происходит по линейному закону в зависимости от времени. Но раскачка заканчивается, когда амплитуда достигает значения, задаваемого формулой (75). Пусть раскачка продолжается в течение времени t, тогда

В этом выражении частота w0 фиксирована. Следовательно, время установления колебаний под действием внешней гармонической силы тем больше, чем выше добротность осциллятора.
Порядки величин добротностей некоторых осцилляторов даны в табл. 3.
Механические (резина) 10 на 100 Гц; 5 на 2*10 3 Гц; 3 на 10 4 Гц;
Акустические резонаторы – 50;
Радиотехнические контуры с частотой
1 МГц – несколько сотен;
Медные резонаторы на СВЧ f >1МГц – 3*10 4 ;
Пьезоэлектрические кристаллы (кварц) – 5*10 5 ;
Колебания ядер атомов в эффекте Мессбауэра – 10 10 ;
Лазерные колебания (резонатор Фабри-Перо) – 5*10 6 ;
Пульсары (нейтронные замагниченные звезды) – 7,5*10 12
(Период 0,033с, замедление вращения и частоты следования импульсов 36,52 нс/сутки = 4,23*10 -13 . Период увеличивается в е раз за 2500 лет).
Рис. 24. Добротность как характеристика различных сторон колебательных процессов
Эти данные могут быть использованы при рассмотрении соответствующих осцилляторов.
При рассмотрении добротности колебаний следует уяснить ее роль в процессе затухания амплитуды колебаний, в потере энергии при затухании колебаний, установить ее связь с шириной частотной полосы колебательного контура по заданному уровню, с продолжительностью установления колебаний, а также с коэффициентом усиления колебаний и воспроизводимостью модуляции при усилении модулированного колебания.
Рассмотренные затухающие колебания характеризуются двумя параметрами β и ω (или ω0). В ряде случаев весьма информативным оказывается их отношение ω/β, называемое добротностью. Аналогично вводится логарифмический декремент затухания. В различных разделах физики и техники определение добротности свое и на это следует обращать внимание. Характеристика различных аспектов колебательных процессов с помощью понятия добротности представлена в таблице 3.
При выполнении работы предполагается, что учащиеся не владеют методами решения дифференциальных уравнений второго порядка. Однако они должны уметь анализировать готовые решения. В приведенной таблице 4 представлены основные колебательные уравнения и их решения. Дифференцированием следует убедиться, что данное решение действительно удовлетворяет указанному уравнению.
Основные колебательные уравнения и их решения
| Гармонические колебания | |
| х 11 + ω0 2 х = 0 | x(t) = Acos(ω0 t — j0) |
| Гармонические колебания около смещенного положения устойчивого равновесия. Реализуются, когда на колеблющуюся материальную точку действует постоянная внешняя сила | |
| х 11 + ω0 2 х = fc | x(t) = х0 + Acos(ω0 t — j0) |
| Гармонические колебания при силе сопротивления пропорциональной скорости | |
| х 11 + 2βх 1 + ω0 2 х = 0 (β — β t cos(ωt + j0). ω 2 = ω 2 0 – β 2 | |
| Гармонические колебания при силе сопротивления пропорциональной скорости и при действии постоянной силы | |
| х 11 + 2βх 1 + ω0 2 х = fc (β — β t cos(ωt + j0). ω 2 = ω 2 0 – β 2 | |
| Гармонические колебания при постоянно действующей внешней силе, которая линейно зависит от времени t. | |
| х 11 + 2βх 1 + ω0 2 х = a + bt | x(t) = A0e — β t cos(ωt + j0)+α+γt, где ω 2 = ω 2 0 – β 2 , γ = b/ ω0 2 , α = a/ ω0 2 — 2 β b/ ω0 4 |
| Колебания под действием внешней гармонической силы. Решение в виде установившихся колебаний | |
| х 11 + 2βх 1 + ω0 2 х = f0 cosωt | x(t) = А cos(ωt — j), где A= f0/(  ), tg j = 2βω/(ω0 2 – ω 2 ). ), tg j = 2βω/(ω0 2 – ω 2 ). |
| х 11 + ω0 2 х = f0 sinωt | x(t) =  |
| Колебания под действием внешней силы, представимой в виде ряда Фурье. Решение в виде установившихся колебаний | |
х 11 + 2βх 1 + ω0 2 х = =  f0i cosωi t f0i cosωi t | x(t) =  Аi cos(ωi t — ji ), где Ai= f0i /( Аi cos(ωi t — ji ), где Ai= f0i /(  ), tg ji = 2βωi /(ω0 2 – ωi 2 ). ), tg ji = 2βωi /(ω0 2 – ωi 2 ). |
| Вынужденные колебания в нелинейной системе | |
| х 11 + ω0 2 х +sx 3 = f0 cosωt | x(t) ≈  ( ω0 2 A + ( ω0 2 A + 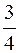 sA 3 — f0 ) cosωt + sA 3 — f0 ) cosωt + 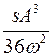 cos3ωt. ( cos3ωt. (  ω0 2 ) ω0 2 ) |
Фазовые траектории
Характер движения материальной точки определяется вторым законом Ньютона, т.е. дифференциальным уравнением 2-го порядка, и начальными значениями координат и скорости (всего 6 величин в самом общем случае). Большинство задач на движение можно свести к движению вдоль одной прямой (например, взяв проекции соответствующих векторов), положим, вдоль оси х. Любое движение осциллятора, при котором меняется одна единственная физическая величина, для которой записано дифференциальное уравнение движения, есть одномерное движение.
Введем ортогональную систему координат x и v(x) . Плоскость, заданную этими координатами назовём фазовой. С течением времени материальная точка в своем движении по фазовой плоскости очерчивает фазовую траекторию v(x). Значения x и v в заданный момент времени определяют изображающую точку. Изображающие точки с координатами f(x, v) = 0 и v= 0 называются особыми точками. Особым точкам соответствуют состояния равновесия системы.
Рассмотрим простой осциллятор и установим основные свойства фазовых плоскостей и фазовых траекторий на его примере. Смещение осциллятора задаётся в виде
Скорость осциллятора найдена дифференцированием x(t)
Исключим время из выражений x(t) и vx(t) . Для этого выразим cos x и sin x, возведем в квадрат и сложим. Получим

Это соотношение дает зависимость v(х) и задает фазовую траекторию движения простого незатухающего гармонического осциллятора. В координатах v,х это эллипс. Для колебаний с различными амплитудами мы получаем семейство подобных эллипсов, поскольку отношение их полуосей эллипса А/A ω0 не зависит от амплитуды А, а определяется постоянным параметром ω0.
2.1.18 а. Свойства фазовых траекторий
1. Семейство фазовых траекторий, отличающихся начальными условиями, т.е. значениями х0,, v0 , являются не двух-, а однопараметрическим, т.к. определяет не х и v поразнь, а их комбинацию, образующую полную энергию Е осциллятора (А = 1)
Е = 
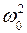
2. Фазовые траектории между собой не пересекаются, т.к. уравнение движения имеет однозначное решение при заданных начальных условиях. Как мы установили, рассматриваемые эллипсы подобны.
3. Назовем точку, взятую на фазовой траектории, изображающей. Отметим, что движение изображающей точки по фазовой траектории происходит по часовой стрелке, поскольку если ее скорость в некоторой точке положительна, то координата х должна возрастать.
4. Установим, что движение изображающей точки М (х, v) происходит вдоль фазовой траектории с постоянной секторной скоростью. Понятие секторной (секториальной) скорости (рис. 25) введено в § 49 (т.1) / 1/. Определим ее в векторном виде по правилу

Здесь 








Рис. 25. К определению секторной скорости
Итак, 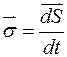


Представим радиус – вектор 













Если х изменяется по гармоническому закону x = А cos(ω0 t + α), vx = -A ω0 sin (ω0t + α), v 1 x = d 2 x/dt = -A ω 2 0 cos (ω0t + α), то после подстановки в (112) будем иметь

Таким образом, секторная скорость изображающей точки на фазовой плоскости есть величина постоянная и равная полной механической энергии осциллятора.
2.1.18 б.Фазовые траектории затухающих колебаний и релаксаций
Рассмотрим затухающее колебание, описываемое дифференциальным уравнением
х 11 + 2βх 1 + ω0 2 х = 0.
Полагая 
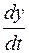
и будем считать, что u и v – прямоугольные координаты.
Тогда из ω 2 01 = ω0 2 – β 2 получим
y 2 + 2 βxy + ω0 2 х = (y +βx) 2 + ω 2 01x 2 = u 2 +v 2 ,
u 2 +v 2 = С 
или, переходя к полярным координатам, получим
ρ 2 = С 
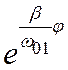
Мы получили уравнение спирали, навивающейся на начало координат.
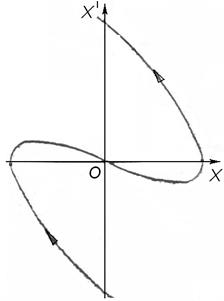
Если теперь перейти к исходным координатам у’,х, т.е. v,x, то в силу линейности преобразования u = ω01x, v = y +βx, интегральные кривые качественно не изменятся и будут также представлять собой спирали (рис. 26). Спирали закручиваются при затухающих колебаниях и разворачиваются при нарастающих.
Фазовые траектории затухающих колебаний, релаксаций и биений представлены на рис. 26 – 28.
Понятия фазовой плоскости и фазовой траектории особенно эффективны при анализе решений нелинейного дифференциального уравнения вида

Это уравнение выражает второй закон Ньютона для точки, на которую действует возвращающая сила сложного вида и силы сопротивления, сложным образом зависящие от скорости 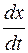
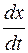
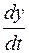
Решением этой системы является пара функций x(t), y(t), задающих в параметрическом виде фазовую траекторию. Параметр t — это, ко-
нечно, время. Характерной особенностью системы (116) является то, что в нее время явно не входит.
Рис.26. Фазовые траектории затухающих колебаний в коор-
.
Рис. 27. Фазовая траектория релаксационных движений
Рис. 28. Фазовая траектория биений
Если окажется, что в некоторой точке M(x0, y0) фазовой плоскости выполняются равенства
то фазовая траектория вырождается в точку. Такие точки называются особенными. Смысл соотношений (117) состоит в том, что в особой точке скорость и ускорение частицы одновременно равно нулю. Это означает, что материальная точка находится в состоянии покоя или равновесия. Состояние равновесия физической системы, описываемой уравнением (116), это особое состояние и поэтому изучение типов особых точек чрезвычайно важно.
При анализе движения на фазовой плоскости стремятся установить:
1) наличие особых точек;
2) различия в расположение фазовых траекторий вблизи особых точек;
3) устойчивость и неустойчивость особых точек, т.е. остается ли с течением времени материальная точка вблизи особой точки фазовой траектории или удаляется от нее;
4) наличие замкнутых траекторий, которые, как и в случае простого гармонического осциллятора, соответствуют периодическому движению.
Обычно ответа на эти вопросы достаточно, чтобы качественно понять характер решения х(t) уравнения (116), не находя аналитического выражения х(t), которое зачастую найти невозможно.
Спектры колебаний
В целом ряде практически важных случаев возникает задача о представлении сложного процесса (колебания, волнового движения, излучения, шума и т.д.) в виде набора (суммы) отдельных гармоник с дискретными или бесконечно близкими частотами. Сама операция носит название гармонического (спектрального) анализа, а набор гармоник – спектром (дискретным или непрерывным). Понятно, что каждая гармоника, представляющая собой монохроматическое (одночастотное) колебание входит в спектр не только со своей определенной частотой, но и с амплитудой, и фазой.
В математическом анализе выясняются возможности представления процессов (функций) в виде тригонометрических рядов, т.е. наборов гармоник. Важнейшие результаты в этом направлении были получены Фурье. В частности, он показал, что если процесс является периодическим, но не гармоническим, то он представляется дискретным спектром (рядом Фурье). Более того, если функция, описывающая процесс, является четной, то соответствующий ряд Фурье представляет собой набор косинусоид, а если нечетной – то синусоид. Если функция свойством четности не обладает, то в наборе присутствуют как синусоиды, так и косинусоиды. Если процесс описывается произвольной (непериодической) функцией, то его можно представить в виде непрерывного спектра – интеграла Фурье по частоте. Мы будем рассматривать только периодические процессы, т. е. ряды Фурье. Особенностью разложения Фурье по гармоникам, в основном определяющей его практические применения является то, что в ряде Фурье гармоники низших частот имеют большие амплитуды, чем гармоники более высоких частот, а в сплошном спектре практически всегда можно выделить определенную группу гармоник, амплитуды которых наиболее значительны. Именно такие гармоники определяют энергетику процесса и позволяют не включать в рассмотрение весь бесконечный набор гармоник.
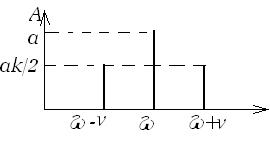
Рассмотрим простейшее сложное колебание – гармонику, модулированную по амплитуде:
x = А cos(ωt — j ) = а(1 + к cosn t) cos(ωt — j )= а cos(ωt — j )+ 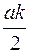
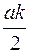
Это сложное колебание мы представили в виде набора трех гармоник с несущей частотой ω и двумя боковыми частотами ω+n и ω -n. Зависимость амплитуд гармоник от частоты называется амплитудным спектром. Для данного случая он представлен на рис. 29. Начальные фазы у всех наших гармоник одинаковы, т.е. фазы не зависят от частоты гармоник. Если в более сложных случаях такая зависимость появляется, то говорят о фазовом спектре. Например, если гармоническое колебание получено в результате сложения двух одночастотных колебаний со своими амплитудами и фазами, то можно говорить об амплитудном и фазовом спектрах. Заметим, что поскольку гармоническое колебание можно разложить на два (и больше) таких же бесконечным числом способов, то говорить о спектрах отдельных гармоник бессмысленно.
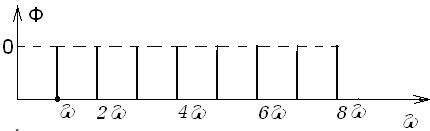
Рассмотрим сложение одночастотных колебаний с одинаковыми амплитудами и равномерно (по линейному закону) нарастающими фазами. Исходные формулы имеют вид (а = ωt, h = φ)
cosa + cos (a + h) +…..+ cos[a + (n-1)h] = 
sina + sin(a+h) +….+ sin[a + (n-1)h]= 
Здесь амплитуды гармоник стоящих слева одинаковы, а их частоты равноотстоят друг от друга. Следовательно, спектр функций, стоящих справа в (119) представляет собой «гребенку» (см. рис. 30).
Другой пример – гребенка с амплитудами, нарастающими в арифметической прогрессии:
cosa+2cos2a+…..+n cos na = 
sina + 2sin2a +….+ n sin na = 
Фазовый спектр также может представлять гребенку (рис. 31).
Примеры разложения процессов в ряды Фурье представлены в таблице в /3/. Приведем несколько примеров.
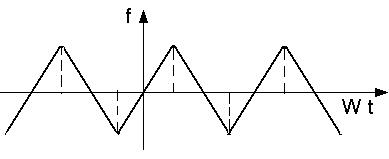
Для четной периодической функции (рис. 32)
f(ωt) = 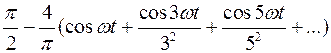
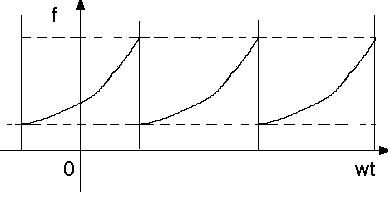
Для нечетной периодической функции (рис. 33)
f(ωt) = 
Для периодической функции, не обладающей свойством четности и заданной на промежутке – π -1 , ω1 = 10 рад/с представлены на рис. 37 — 40.
Рис. 29. Амплитудный спектр модулированного по амплитуде колебания
Рис. 30. Дискретный амплитудный спектр «гребенка» (119)
Рис.31. Фазовый спектр «гребенки»
Рис. 32. Дискретный амплитудный спектр (по формуле (120))
Рис. 33. Равномерный фазовый спектр
Рис. 34. Четная функция, описывающая колебательный процесс
Рис. 35. Нечетная функция, описывающая колебательный процесс
Рис. 36. Колебательный процесс, описываемый функцией, которая не обладает свойством четности
Рис. 37. Косинусный спектр затухающего колебания
Рис.38. Синусный спектр затухающего колебания
Рис.39. Фазовый спектр затухающего колебания
 |
Рис. 40. Амплитудный спектр затухающего колебания
Рис.41. Векторная диаграмма, спектр и вид колебания, являющегося суммой гармоник с одинаковыми амплитудами и фазами, частоты которых нарастают в арифметической прогрессии
При суммировании конечного (или бесконечного) числа гармоник в узком спектральном диапазоне получаются функции, представляющие пакеты. Их часто называют волновыми. Дело в том, что волна, приходя в данную точку пространства, возбуждает в ней колебания. Если в эту же точку в данный момент времени приходят другие волны, то колебания, создаваемые ими, складываются тем или иным образом. Ранее (72 — 73) мы показали, что колебания разных частот можно сложить как колебания одной частоты, но с разными фазами. Наиболее практически важным является случай суммирования гармоник с дискретным набором равноотстоящих частот сосредоточенных в определенном интервале (рис. 41).
2.1.20. Нелинейные колебания
Нелинейные колебания совершаются тогда, когда силы, действующие на осциллятор (возвращающая, трения) описываются нелинейными функциями (рис. 2, раздел 2.1.14, (100)). Простейшим видом нелинейных колебательных процессов являются процессы в системе, компоненты которой конкурируют между собой /5/. Например, при эксплуатации техники конкурентными процессами являются ремонт (восстановление функций) и износ (старение). Для двух конкурирующих процессов задача нахождения динамики их изменения во времени была решена еще В. Вольтерра применительно к определению численности популяций в системе хищник — жертва (зоологическая или ботаническая модель). Оказалось, что математические модели ряда основных процессов, протекающих в организмах и клетках, в технических системах, в обществе сходны с моделью Вольтерра.
Пусть х – число жертв (зайцев), а у – число хищников (волков). В простейшем случае скорость изменения численности жертв определяется скоростью их размножения пропорциональной их количеству х, а также их гибелью от встреч с хищниками, которая пропорциональна произведению ху. Скорость изменения численности хищников определяется наличием пищи, т.е. пропорциональна величине ху, и скоростью их гибели, пропорциональной их числу у.
Пусть х – количество объектов, подлежащих восстановлению (ремонту), а у – затраты ресурсов (материальных, энергетических, финансовых). Скорость появления объектов х зависит от их количества, и, в частности, может быть пропорциональна этому количеству. Кроме того, в силу ограниченности ресурсов, скорость изменения объектов х пропорциональна выделению ресурсов у (не всегда хватает средств на ремонт всех объектов), т.е. произведению ху. Скорость выделения ресурсов у определяется наличием объектов ремонта х и может считаться пропорциональной х, а также величине ху. Коэффициенты перед ху в обоих случаях в принципе должны быть различными, т.к. выделенные ресурсы могут быть распределены потребителем по своему усмотрению (например, на чрезвычайные и аварийные ситуации).
В математическом виде имеем систему дифференциальных уравнений, описывающую указанные процессы:
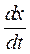

Здесь коэффициенты k – постоянны, а х и y — функции времени t.
Простота модели не только в том, что она двухкомпонентная, но и в том, что мы пренебрегаем другими многочисленными взаимодействиями между количествами х и у, считая указанные основными.
Система (128) нелинейна по причине наличия произведения ху. Стандартный метод решения таких систем состоит в их линеаризации, т.е. в получении стационарных (не зависящих от времени) решений и рассмотрении малых отклонений от стационарного состояния. Поскольку зависимость от времени исключена, то х0 = const и у0 = const. Следовательно,

и при этом (128) превращается в алгебраическую систему
у0 = 
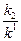
Теперь ищем решение системы (128) в виде
Подставляем (129) в (128), имеем:

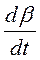
Членами kαβ и k 1 αβ можно пренебречь, т.к. они содержат произведение двух малых величин, х0 и у0 уже найдены. В результате получаем линеаризованную систему:


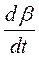

Продифференцируем первое уравнение по t и подставим 

Продифференцируем второе уравнение из (130) по t и подставим 
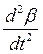
Уравнения (131) и (132) – стандартные уравнения колебаний. Частота колебания численности жертв и хищников одинакова и равна ω0 = 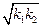
Эти функции описывают гармонические колебательные процессы около смещенного положения равновесия.
http://lektsii.org/12-57909.html