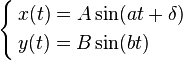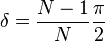Фигуры Лиссажу
Что такое фигуры Лиссажу?
Фигуры Лиссажу представляют из себя различные геометрически-красивые рисунки, которые вычерчиваются точкой, колеблющейся в двух взаимно-перпендикулярных направлениях на одной плоскости.
Чтобы было более понятно, давайте представим девочку на качели из покрышки:
И вот представьте, что сзади ее раскачивает папа, а сбоку — мама. То есть наша девочка будет одновременно летать вперед-назад, а также влево-вправо. Долго ли она продержится — это уже другой вопрос). Если в солнечный денек посмотреть на землю, то мы увидим, что тень девочки вырисовывает различную траекторию полета.
Почему бы нам не поиграться пучком электронов, отклоняя его одновременно и по вертикали и по горизонтали? Вспоминаем, как выглядит электронно-лучевая трубка осциллографа:
1 — это горизонтальные пластины
2 — вертикальные пластины
ну и остальные детали — это составляющие электронной пушки.
Подаем на вертикальные пластины один синусоидальный сигнал, а на горизонтальные — другой синусоидальный сигнал. В результате точка на осциллографе будет вырисовывать различные линии и кривые, в зависимости от частоты сигналов. Хотя, цифровой осциллограф и аналоговый почти не похожи по внутренней начинке, но принцип действия у них все равно схож.
Как получить фигуры Лиссажу
Итак, для того, чтобы вырисовывать фигуры Лиссажу, нам потребуются два генератора частоты.
и осциллограф с функцией XY-режима. В моем случае это цифровой осциллограф OWON
Думаю, почти во всех современных осциллографах есть режим XY, будь это аналоговый или цифровой осциллограф.
Режим XY-осциллографа
Как вы помните, при простом использовании осциллографа у нас по оси X было время, а по оси Y — напряжение. Поэтому, по умолчанию, мы на осциллографе смотрим изменение напряжения во времени. Но если с помощью нехитрой кнопки переключить в режим XY, то у нас по Y будет напряжение и по X…. тоже напряжение, но уже с другого генератора частоты. Если включить в таком режиме только один генератор, то мы увидим только одну прямую линию либо по вертикали, либо по горизонтали. Это аналогично тому, если бы нашу девочку раскачивал только папа или только мама. Наша девочка летела бы только по одной прямой траектории.
А что будет, если сбоку нашу девочку будет раскачивать мама, а сзади — папа? Тут уже траектория девочки будет хаотичной. Но во всяком хаосе рождается порядок. И первым его заметил французский математик Жюль Антуан Лиссажу.
Строим фигуры Лиссажу на осциллографе
Цепляем на один канал один генератор частоты, а на другой канал — другой генератор частоты:
На осциллографе мы должны увидеть два сигнала с разных генераторов частоты, благо у меня осциллограф двухканальный:
Теперь переводим осциллограф в режим XY. На моем осциллографе это делается с помощью кнопки Display
Ну а потом с помощью дисплейных клавиш выбираем режим XY
И получается примерно вот такая хаотическая картинка:
Ну еще бы, один генератор дергает точку по X, другой по Y и у каждого генератора разная частота.
А давайте возьмем один генератор и с него подадим сигнал на два канала сразу. Частота и фаза совпадают и на первом и втором канале, так как мы берем сигнал с одного и то же генератора. В результате у нас будет вот такая картинка:
Если взять 100 Герц на первом генераторе и на втором генераторе, то получим что-то типа этого:
В реальности же получается круг, который все время крутится и превращается то в эллипс, то в прямую, так как очень ровно подобрать частоту на первом и втором генераторе очень сложно. Хотя на практике можно подавать сигнал на один канал напрямую, а на другой — через фазовращатель.
Если увеличить частоту на одном из генераторов вдвое, то можно наблюдать уже другие фигуры:
Эта фигура тоже все время крутится на осциллографе.
Увеличиваем на одном генераторе частоту в кратное число раз, то есть было 100, потом 200, 300 и тд и получаем абсолютно новые 3D фигуры 😉
Различное отношение частот одного генератора к другому дает различные фигуры Лиссажу:
Вот такие фигуры вы будете видеть на экране своего осциллографа:
А вот такие фигуры Лиссажу получаются, если использовать пилообразный сигнал с обоих генераторов сразу при разных отношениях коэффициентов


А вот такие фигуры получаются, если на одном оставить синус, а на втором поставить пилу:

В основном фигуры Лиссажу в электронике можно использовать тогда, когда надо узнать частоту неизвестного генератора через образцовый генератор, частоту которого мы знаем, а также узнать сдвиг фаз между двумя одинаковыми сигналами. Ну и второе применение — это чисто визуальный кайф при вращении этих фигур на экранчике вашего осциллографа 😉
ЛИССАЖУ́ ФИГУ́РЫ
В книжной версии
Том 17. Москва, 2010, стр. 578
Скопировать библиографическую ссылку:
ЛИССАЖУ́ ФИГУ́РЫ, замкнутые плоские кривые, описываемые точкой, движение которой является суперпозицией двух взаимно перпендикулярных колебаний с отношением частот, равным рациональному числу. Впервые были подробно изучены франц. математиком Ж. А. Лиссажу в 1857–58. Л. ф. описываются системой параметрич. уравнений (параметр – время $t$ ) $$x=A_1\text
Сложение перпендикулярных колебаний. Фигуры Лиссажу.
| |
|
Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Жюлем Антуаном Лиссажу. Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или 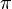
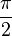
Математическое выражение для кривой Лиссажу[править | править вики-текст]
где A, B — амплитуды колебаний, a, b — частоты, δ — сдвиг фаз
Вид кривой сильно зависит от соотношения a/b. Когда соотношение равно 1, фигура Лиссажу имеет вид эллипса, при определённых условиях она имеет вид окружности(A = B, δ = π/2 радиан) и отрезка прямой (δ = 0). Ещё один пример фигуры Лиссажу — парабола (a/b = 2, δ = π/2). При других соотношениях фигуры Лиссажу представляют собой более сложные фигуры, которые являются замкнутыми при условии a/b — рациональное число.
Фигуры Лиссажу, где a = 1, b = N (N — натуральное число) и
являются полиномами Чебышёва первого рода степени N.
| | | следующая лекция ==> | |
| Метод векторных диаграмм. Рассмотрим вращающийся против часовой стрелки с постоянной угловой скоростью w вектор А | | | Неинерциальные системы отсчета. Описание движения в неинерциальных системах. Силы инерции. Центробежная сила. Сила Кориолиса. |
Дата добавления: 2016-01-29 ; просмотров: 9555 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://bigenc.ru/physics/text/2175554
http://helpiks.org/6-64688.html





























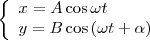 (1) где α — разность фаз обоих колебаний, А и В равны амплитудам складываемых колебаний. Уравнение траектории результирующего колебания определим исключением из формул (1) времени t. Записывая складываемые колебания как
(1) где α — разность фаз обоих колебаний, А и В равны амплитудам складываемых колебаний. Уравнение траектории результирующего колебания определим исключением из формул (1) времени t. Записывая складываемые колебания как 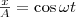
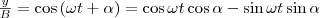 и заменяя во втором уравнении
и заменяя во втором уравнении  на
на 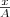 и
и 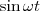 на
на 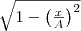 , найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей:
, найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей: 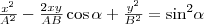 (2) Поскольку траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными. Размеры осей эллипса и его ориентация зависят от амплитуд складываемых колебаний и разности фаз α. Рассмотрим некоторые частные случаи, которые представляют для нас физический интерес: 1) α = mπ (m=0, ±1, ±2, . ). В этом случае эллипс становится отрезком прямой
(2) Поскольку траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными. Размеры осей эллипса и его ориентация зависят от амплитуд складываемых колебаний и разности фаз α. Рассмотрим некоторые частные случаи, которые представляют для нас физический интерес: 1) α = mπ (m=0, ±1, ±2, . ). В этом случае эллипс становится отрезком прямой 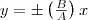 (3) где знак плюс соответствует нулю и четным значениям m (рис. 1а), а знак минус — нечетным значениям m (рис. 2б). Результирующее колебание есть гармоническое колебание с частотой ω и амплитудой , которое совершается вдоль прямой (3), составляющей с осью х угол . В этом случае имеем дело с линейно поляризованными колебаниями; 2) α = (2m+1)(π/2) (m=0, ± 1, ±2. ). В этом случае уравнение станет иметь вид
(3) где знак плюс соответствует нулю и четным значениям m (рис. 1а), а знак минус — нечетным значениям m (рис. 2б). Результирующее колебание есть гармоническое колебание с частотой ω и амплитудой , которое совершается вдоль прямой (3), составляющей с осью х угол . В этом случае имеем дело с линейно поляризованными колебаниями; 2) α = (2m+1)(π/2) (m=0, ± 1, ±2. ). В этом случае уравнение станет иметь вид 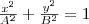 (4) Это есть уравнение эллипса, у которого оси совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис. 2). Если А=В, то эллипс (4) превращается в окружность. Такие колебания называются циркулярно поляризованными колебаниями иликолебаниями, поляризованными по кругу.
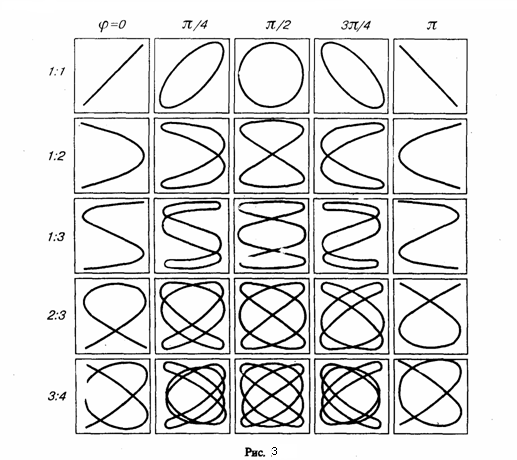
(4) Это есть уравнение эллипса, у которого оси совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис. 2). Если А=В, то эллипс (4) превращается в окружность. Такие колебания называются циркулярно поляризованными колебаниями иликолебаниями, поляризованными по кругу. 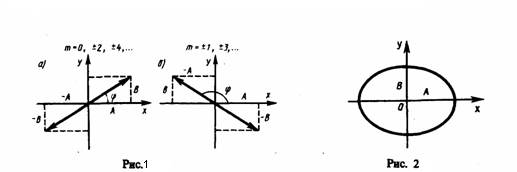 Если частоты складываемых взаимно перпендикулярных колебаний имеют различные значения, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, которая совершает одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Вид этих замкнутых кривых зависит от соотношения амплитуд, разности фаз и частот складываемых колебаний. На рис. 3 даны фигуры Лиссажу для различных соотношений частот (даны слева) и разностей фаз (даны вверху; разность фаз равна φ). Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, которые параллельны осям координат. По виду фигур можно найти неизвестную частоту по известной или найти отношение частот складываемых колебаний. Поэтому анализ фигур Лиссажу — широко применяемый метод исследования соотношений частот и разности фаз складываемых колебаний, а также формы колебаний.
Если частоты складываемых взаимно перпендикулярных колебаний имеют различные значения, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, которая совершает одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Вид этих замкнутых кривых зависит от соотношения амплитуд, разности фаз и частот складываемых колебаний. На рис. 3 даны фигуры Лиссажу для различных соотношений частот (даны слева) и разностей фаз (даны вверху; разность фаз равна φ). Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, которые параллельны осям координат. По виду фигур можно найти неизвестную частоту по известной или найти отношение частот складываемых колебаний. Поэтому анализ фигур Лиссажу — широко применяемый метод исследования соотношений частот и разности фаз складываемых колебаний, а также формы колебаний.