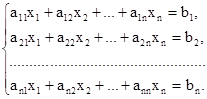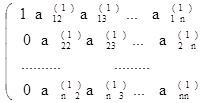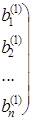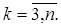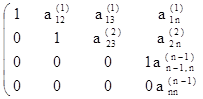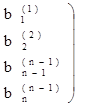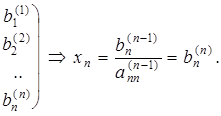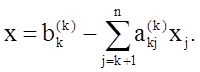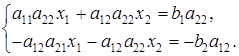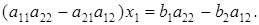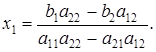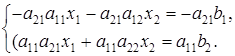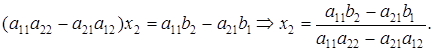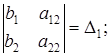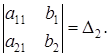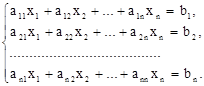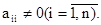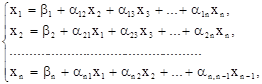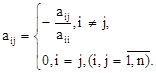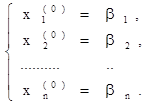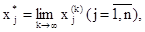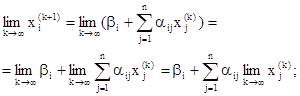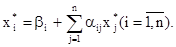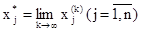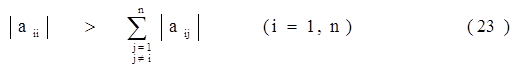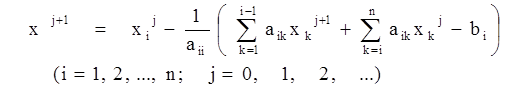Точные и приближенные методы решения систем линейных уравнений
Самое простое уравнение — это линейное уравнение с одной переменной х вида:
Обобщением таких уравнений является линейное уравнение с несколькими переменными х1, х2, . хn вида:
Многие задачи сводятся к решению конечного множества уравнений вида (2), то есть системы линейных уравнений. В общем виде система n линейных уравнений с n переменными x1, x2. xn записывается как совокупность числовых равенств:
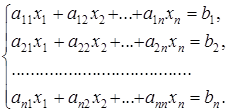
Коэффициенты aij системы для их упорядочения снабжаются двумя индексами, причем индекс i соответствует номеру строки, а j —номеру столбца (i = 1, 2. n; j = 1, 2. n). Тогда свободный член запишется в виде bi(i = 1, 2. n), а переменная— хj (j = 1, 2. n). Будем далее считать, что упорядоченные наборы чисел aij, xj и bi берутся из множества действительных чисел R. Решением системы (3) n уравнений с n переменными называют упорядоченную совокупность n чисел c1, c2, . cn 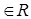
В частном случае, при n = 2 и n = 3 получаем хорошо знакомые системы двух линейных уравнений с двумя переменными:
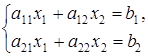
и трех линейных уравнений с тремя переменными:
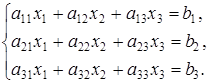
Решением системы (4) является упорядоченная пара чисел (c1, c2), а решением системы (5) — упорядоченная тройка чисел (с1, c2, c3).
Известно, что исследование и нахождение решения для систем (4) и (5) не представляют особых трудностей. Но задачи практического содержания сводятся к исследованию и решению систем линейных уравнений, содержащих десятки, сотни и даже тысячи переменных. Число элементарных операций при решении линейных систем с n переменными пропорционально примерно n 3 , поэтому решение таких задач стало возможным только с появлением быстродействующих ЭВМ.
Не останавливаясь на вопросах исследования систем линейных уравнений, в дальнейшем будем предполагать, что система имеет единственное решение. Поэтому основной задачей этой главы и будет изучение универсальных вычислительных алгоритмов, используемых для нахождения единственного решения системы линейных уравнений, когда число переменных совпадает с числом уравнений.
Методы решения систем линейных уравнений можно разделить на две группы: точные и итерационные (приближенные) методы.
Точными являются такие методы, которые позволяют получить решение системы после выполнения конечного числа арифметических операций над коэффициентами системы и их свободными членами. Причем решение получится точным только тогда, когда коэффициенты и правые части системы (3) известны точно и все арифметические действия над ними выполняются без округлений. Из точных методов рассмотрим метод Гаусса и правило Крамера. Однако на практике даже этими методами не всегда удается получить точное решение, ибо в ЭВМ точные коэффициенты представляются приближенно с некоторой погрешностью, а в процессе вычислений необходимо проводить округление чисел.
Итерационными являются методы, позволяющие получать решение системы с заданной точностью путем сходящихся бесконечных процессов. Из приближенных методов рассмотрим ниже метод итераций.
4.1 Алгоритм метода Гаусса
Пусть дана система n линейных уравнений с n переменными:
Коэффициенты аij при переменных будем рассматривать как элементы двумерного массива A (N, N), а свободные члены bi— как элементы одномерного массива В (N). Решение xi(i = 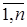
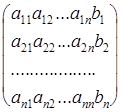
Предписываемые методом Гаусса преобразования будем выполнять над элементами расширенной матрицы. Опишем формально алгоритм решения линейной системы методом Гаусса без выбора главного элемента.
1. Элементы первой строки расширенной матрицы (А | В)делим на а11. Полученную после такого деления первую строку умножаем последовательно на ak1(k = 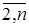
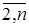
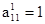

2. Элементы второй строки расширенной матрицы делим на 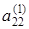
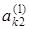
3. Продолжаем этот процесс исключения переменных (получения нулей) до тех пор, пока подобная процедура не будет проделана с (n — 1)-й строкой матрицы. После этого получим матрицу:

4. Элементы n-й строки делим на 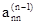

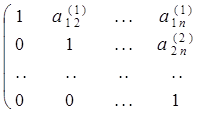
На этом закончился прямой ход метода Гаусса.
5. Выполняем обратный ход метода Гаусса: в (п—1)-ю строку последней матрицы подставляем значение хn и находим значение xn-1, затем последовательно находим xn-2, xn-3, . , x2, x1 по формулам:
Этот алгоритм является экономичным в смысле использования памяти, так как все промежуточные и окончательные значения элементов в процессе преобразования матриц последовательно хранятся в тех же ячейках памяти, что и массивы А и В. Очередные значения диагональных элементов 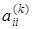
Значения переменных xn, xn-1, . x1 присваиваются элементам массива свободных членов В.
Метод Гаусса с выбором главного элементазаключается в том,что при прямом ходе производится выбор наибольшего по модулю (главного) элемента и перестановка строк или столбцов. Последнее исключает деление на 0, если матрица коэффициентов содержит нулевые элементы, и повышает точность вычислений при наличии ошибок округления. Обычно для программ, ведущих вычисления с числами с плавающей точкой, достаточен выбор Aii ¹ 0.
Метод вращения является разновидностью метода Гаусса. Он обладает повышенной устойчивостью к “провалам” промежуточных вычислений. Этот метод обеспечивает приведение исходной системы к системе с верхней треугольной матрицей (см. литературу).
4.2 Правило Крамера
Правило Крамера рассмотрим на примере двух линейных уравнений с двумя переменными:
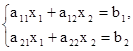
хотя оно применимо и для решения системы n линейных уравнений с n переменными, но с увеличением n требует большого объема вычислительной работы.
Умножим первое уравнение системы (17) на коэффициент а22, а второе — на — a12 и полученные уравнения сложим. Тогда имеем:
Если a11a22 — a21a12 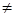
Аналогично, умножая первое уравнение системы (17) на —a21, второе — на а11 и складывая их, получаем:
Введем обозначения: a11a22 — a21a12 = 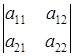

b1a22 — b2a12 =
a11b2 — a21b1 =
Следовательно, 
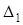

B = 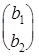
Определитель 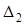
Определитель 


Если главный определитель 
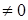
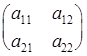
Таким образом, если главный определитель системы уравнений (17) 
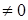
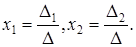
Формулы (18) называются формулами Крамера.
Нахождение решения линейной системы (17) по формулам (18) называется правилом Крамера, который одним из первых пришел к понятию определителя и доказал сформулированное выше предложение.
Справедливы также следующие два предложения:
1. Если главный определитель системы (17) 


2. Если все три определителя 


Легко дать геометрическое истолкование этим предложениям. Поскольку каждому уравнению системы (17) в плоскости соответствует некоторая прямая, то система (17) имеет единственное решение, если прямые имеют одну общую точку; не имеет решений, если прямые параллельны; и имеет бесконечное множество решений, если прямые сливаются.
Правило Крамера решения системы n линейных уравнений с n переменными имеет определенное теоретическое значение; практически им уже при n = 4 не пользуются. Установлено, что число операций умножения и деления, которые необходимо выполнить при решении линейной системы алгебраических уравнений порядка n по формулам Крамера, равно:
N(n)= (n 2 — 1)n! + n,
а по схеме единственного деления метода Гаусса:
N(n) = 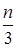
Для сравнения объема вычислительной работы по этим двум алгоритмам подсчитаем количество операций:
по Крамеру по Гауссу
при n = 5 2885 65
при n =10 360*10 6 430
Поэтому все современные ЭВМ имеют стандартные подпрограммы, реализующие различные модификации метода Гаусса.
4.3 Метод итераций и метод Зейделя
Метод итераций позволяет получить последовательность приближенных значений, сходящуюся к точному решению системы линейных уравнений. В отличие от метода Гаусса, метод итераций не требует контроля промежуточных вычислений, так как отдельные ошибки на каком-либо шаге итерации не искажают окончательных результатов, хотя и удлиняет процесс счета. Иначе говоря, метод итераций решения систем линейных уравнений является самоисправляющимся. Кроме того, метод итераций легко запрограммировать для ЭВМ. Пусть имеем систему
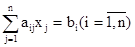
Предположим, что определитель системы отличен от нуля и что диагональные коэффициенты
Выразим из первого уравнения x1, из второго x2, и т. д. Тогда получим эквивалентную систему:
где 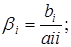
Полученную систему запишем так:
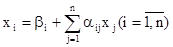
и назовем ее системой нормального вида.
Будем решать ее методом последовательных приближений. За нулевое приближение возьмем, например, столбец свободных членов
Подставив в правую часть системы (20) значения 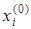
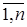
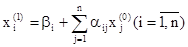
Затем аналогично второе: 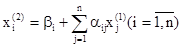
Таким образом, зная k-e приближение, (k + 1)-е приближение вычисляют по формуле 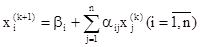
Если последовательность приближений ( 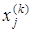
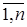
то 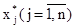
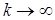
Описанный метод последовательных приближений называется методом итераций. Рабочие формулы метода итераций имеют вид:
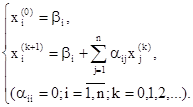
гарантирует теорема о достаточном признаке сходимости процесса итераций.
Достаточным условием сходимости итерационных методов является условие
При методе Зейделя итерационный процесс подобен описанному для метода простых итераций, однако уточненные значения Хi j+1 сразу подставляются в последующие уравнения. Формула итерационного процесса имеет вид:
Дата добавления: 2015-03-11 ; просмотров: 1176 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Информатика, часть 1. «Численные методы»
Государственный комитет РФ по связи и
Сибирский государственный университет
телекоммуникаций и информатики
Методические указания предназначены для студентов заочного отделения инженерно-технических факультетов, изучающих вычислительную технику и программирование в 3-м семестре. Они содержат необходимый теоретический минимум, задачи для курсовой работы и рекомендуемую литературу.
Кафедра прикладной математики и кибернетики.
Для специальностей 2305, 2306, 2307.
Список литературы – 9 наименований.
Утверждено редакционно-издательским советом СибГУТИ в качестве методических указаний.
© Сибирская государственная академия
телекоммуникаций и информатики, 1999 г.
1. Введение
Для современных инженерно-технических задач необходимо использовать сложный математический аппарат и развитые методы их решения. При этом часто приходится встречаться с задачами, для которых аналитическое решение, т. е. общее решение в виде аналитического выражения, связывающего исходные данные задачи с требуемыми результатами, либо вообще невозможно, либо выражается такими громоздкими формулами, что использование их для практических целей явно нецелесообразно.
В этом случае применяются численные методы решения, которые позволяют достаточно просто получить решение поставленной задачи. Численные методы легко реализуются на ЭВМ с помощью вычислительных алгоритмов.
Все многообразие численных методов подразделяют на две группы — точные и приближенные.
Точными называют методы, позволяющие решить задачу в точной постановке. Точные методы не вносят погрешностей в вычисления.
Бывает так, что решить задачу в точной постановке трудно или даже невозможно. Тогда ее заменяют близкой по результатам приближенной задачей. Численный метод, реализующий такую приближенную задачу, называют приближенным методом. Приближенные методы вносят погрешности в вычисления.
Численные методы реализуются конечными или бесконечными вычислительными алгоритмами.
Приближенные методы, основанные на последовательном приближении к решению путем многократного применения какой-либо вычислительной процедуры, называют итерационными методами. В итерационных методах исходными данными для каждой последующей вычислительной процедуры являются результаты применения предыдущих процедур. Итерационные методы позволяют получить приближенное решение, сколь угодно мало отличающееся от точного решения.
Настоящие методические указания содержат основы курса «Численные методы». Для более детального изучения данного курса следует воспользоваться рекомендуемой литературой. Кроме того, для выполнения курсовой работы необходимо использовать знания, полученные в предыдущем семестре в процессе изучения курса «Вычислительная техника и программирование».
2. Абсолютная и относительная погрешность
Определения
Определение. Абсолютной погрешностью величины x называется величина

Следствие этой формулы:
Пример. Результат измерений длины комнаты – 10,2 ± 0,01 м.
Здесь, 10,2 м – приблизительное значение – результат измерений, 0,01 – погрешность измерений – абсолютная погрешность.
Обычно должно быть D x ú -1 ï + ú 2 ï; ï -5 ï > ú -2 ï + ú 1 ï; ï 4 ï > 1 + ú -2 ï.
После этого приводим систему к виду, удобному для итераций.
Получаем: 

Аналогично находятся последующие приближения X(3), X(4) и т. д.
Сравнив 


4. Решение нелинейных уравнений
Если непрерывная функция f(x) принимает значения различных знаков на концах отрезка [a, b], то есть f(a)×f(b)
Точные и приближенные методы решения систем уравнений
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Электронный образовательный курс «Точные и приближенные методы решения систем уравнений» — это электронный ресурс, который содержит полный комплекс учебно-методических материалов, необходимых для освоения данной темы согласно учебному плану в рамках образвательной программы.
Курс обеспечивает все виды работ в соответствии с программой дисциплины, включая практикум, средства для контроля усвоения качества материала.
Основные цели создания электронного образовательного курса:
Повышение качества обучения при релизации образовательных программ с применением электронного обучения и дистационных образовательных технологий.
Оптимизация деятельности педагогического состава,работующего с применением электронного обучения и дистационных образовательных технологий.
Создание электронной информационно-образовательной среды, позволяющей осуществлять индивидуальный подход в образзовательном процессе.
Задачи создания электронного образовательного курса:
Соответствие единым требованиям к структре, отдельным элементам ЭОК и технологиям обучения в системе дистационного образования Ipsilon
Обеспечение образовательного поцесса учебно-методическими и контрольноизерительными материалами по теме «Точные и приближенные методы решения систем уравнений», реализуемой в системе дистанционного образования Ipsilon
Постоянное совершенствование и обновление комплекса учебно-методических материалов по данной теме.
Изучение данной темы является разделом традиционным и важным во всех периодах школьного образования. Данная работа актуальна с точки зрения освоения материала, для практического знания математики не только в курсе школьной программы, но и в углубленном изучении, а так же для практического применения.
Цель считается достигнутой, если ученик на уровнях:
а) имеет понятие о системах уравнений; б) решает системы методом подстановки, алгебраического сложения; в) сравнивает решение однотипных систем базового уровня сложности
а)правильно воспроизводит и использует термины, полученные знания в работе с различными методами решения систем уравнений ; б) имеет представление о системах однородных уравнений, выделяет базис доказательства; в) обобщает решение однотипных задач одного типа, составляет приемы их решения с помощью подсказки.
а) самостоятельно использует полученные знания; б)владеет матричным методом; в)разбирается и самостоятельно решает все виды систем, различными методами.
Цель 1 : контроль усвоения теоретических знаний при работе: а) с основными определениями; б) с методами решения систем уравнений; в) с типами и классами предлагаемых задач.
Цель считается достигнутой, если ученик на уровнях:
а) воспроизводит схему определения понятий и формулирует определения систем; приводит примеры; перечисляет методы решения; вставляет пропущенные в определении слова; раскрывает термин понятия; подводит объект под понятие; б) решает задачи базового уровня сложности.
а) формулирует определение систем уравнений, приводит контрпримеры; умеет доказывать и разбирается в методах решения; б) выполняет доказательство на своей модели; заполняет пустую готовую схему доказательства; называет базис доказательства; воспроизводит план доказательства; в) решает задачи среднего уровня сложности.
а) Работает с предоставленными задачами конкретного уровня, формулирует определение методов Гусса, Крамера и т.д. б) описывает основную идею доказательства; указывает на особенности методов; в) решает задачи повышенного уровня сложности.
Цель 2 : применение знаний и интеллектуальных умений при решении геометрических и учебных задач.
Цель считается достигнутой, если ученик на уровнях:
решает задачи своего уровня сложности: по готовым задачам определяет каким методом необходимо решить данную систему, по неполному условию находит и обосновывает применение метода, по условию без требования, решает системы, используя помощь.
Цель 3 : формирование коммуникативных умений через включение в групповую работу; взаимопомощь, рецензирование ответов, организацию взаимоконтроля и взаимопроверки на всех уровнях.
Цель считается достигнутой, если ученик:
а) работая в группе, ведет активную работу,оказывает помощь, анализирует ответы товарищей по выполненным заданиям предыдущих уровней с обоснованием, организует взаимоконтроль; б) оказывает помощь работающим на предыдущих уровнях; в) составляет контрольную работу в соответствии со своим уровнем освоения темы.
Цель 4: формирование организационных умений (целеполагание, планирование, реализация плана, саморегуляция универсальных познавательных действий).
Цель считается достигнутой, если ученик:
формулирует цели своей учебной деятельности; б) выбирает задачи и решает их; в) осуществляет самопроверку; г) составляет контрольную работу для своего уровня усвоения; д) оценивает свою итоговую деятельность по данным объективным критериям; по собственным критериям, сравнивая их с объективными критериями; е) делает выводы о дальнейших действиях, планирует коррекцию учебной познавательной деятельности.
Успешное освоение данного электронного образовательного курса окажет помощь при сдаче Основного государственного экзамена (ОГЭ) и Единого государственного экзамена (ЕГЭ).
Структура электронного образовательного курса
Предлагается следующий порядок изучения данного электронного курса. Сначала необходимо ознакомиться с модулем «Историческая справка». Данный модуль носит ознакомительный характер, поэтому можно сразу приступить к изучению модуля «Теоретическая часть». Этот модуль достаточно объемный, поэтому на его изучение отводится несколько дней. Учащиеся должны будут ознакомится с основными определениями, освоить различные методы решения систем таких как: метод подстановки, метод алгебраического сложения, метод введения новых переменных, метод замены переменных, далее ученик переходит на изучение более сложного методического материала, знакомится с системами однородных уравнений а также с матричным методом.
Далее учащимся после модуля «Теоретическая часть» предлагаются контрольные вопросы. Правильный ответ на каждый вопрос оценивается в полбалла. Вопросов всего 15, поэтому об успешном прохождении модуля можно будет говорить, набрав от 5 до 7,5 баллов (10-15 вопроса).
После изучения данных разделов можно браться за решение задач базового уровня сложности – это модуль 4. Каждая задача данного уровня будет оцениваться в 1 балл. Модуль считается успешно пройденным, если учащийся набрал от 5 до 7 баллов. Такое количество баллов можно приравнять к оценке «5». Если учащийся набрал от 4 до 5 баллов, это говорит о менее успешном освоении модуля и приравнивается к оценке «4», от 2 до 4 баллов – это оценка «3». Наконец, если набрано менее 7 баллов, значит, есть необходимость снова вернуться к изучению теоретической части.
После того как ученик освоил базовый уровень сложности, он переходит к модулю 5 «Тренировочные задачи среднего уровня сложности». Там также предлагаются 10 заданий, каждое из которых оценивается в 2 балла. Общее количество баллов, которое можно набрать на данном этапе составляет 14 баллов. Модуль считается успешно пройденным, если учащийся набирает от 10-14 баллов. Минимальное количество баллов которое может получить учащимся по прохождению данного теста составляет 6 баллов (3 задания)
Соответственно, 6 – 8 баллов – это оценка «3», 8 – 10 баллов – это оценка «4», 10-14 баллов – это оценка «5». Перевод в оценку необходим для самоконтроля, поэтому, если учащийся набрал менее 6 баллов, он получает оценку «2» и ему необходимо снова обратиться к теоретическому материалу.
Если ученик заинтересован на более углубленное изучение данной темы, ему рекомендуется вернуться в модуль 2″Теоретическая часть» и ознакомится с матричным методом решения систем уравнений. После изучения и освоения материала, предлагается приступить к модулю 6 «Тренировочные задачи повышенного уровня сложности». Таких заданий так же предлагается 7 и правильное решение каждой оценивается в 3 балла. Максимальное количество баллов, которое возможно набрать, составляет- 21 балл (7 заданий). Если учащийся набирает менее 9 баллов, говорит о том. что ему необходимо вернуться в модуль 2″Теоретический материал».
На освоение данного электронного образовательного курса в среднем можно затратить неделю. Но это касается учащихся 9-х классов, освоивших темы, необходимые для решения некоторых задач среднего и повышенного уровней сложности. Необходимо учитывать уровень знаний учащихся, и в каком классе предлагается прохождение данного курса.
Термин «С истема уравнений» — это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.
Существует множество методов решения системы уравнений. Подход зависит от типа системы. Так, решение систем линейных уравнений полностью исследовано: у них найдены аналитические методы ( метод Крамера ) и предложено несколько численных как точных (простейший — метод Гаусса ), так и приближённых ( метод итераций ).
Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.
Габриель Крамер ( нем. Gabriel Cramer , 31 июля 1704 , Женева , Швейцария — 4 января 1752 , Баньоль-сюр-Сез, Франция ) -швейцарский математик, ученик и друг Иоганна Бернулли , один из создателей линейной алгебры .
И звестная теорема линейной алгебры, которая называется правилом Крамера, дает решение системы линейных уравнений в терминах определителей. Крамер опубликовал ее в книге “Введение в анализ алгебраических кривых” («Introduction à l’analyse des lignes courbes algébraique», 1750 год). В этой фундаментальной работе, в которой теория алгебраических кривых описана на основании ньютоновских принципов, впервые доказано, что кривая степени задается заданием ее точек. Для доказательства этого факта Крамера рассмотрел систему линейных уравнений, которую и решил новым методом, получившим название “метода Крамера”.
Иоганн Карл Фридрих Гаусс ( нем. Johann Carl Friedrich Gauß ; 30 апреля 1777 , Брауншвейг — 23 февраля 1855 , Гёттинген ) — немецкий математик , механик , физик , астроном и геодезист . Считается одним из величайших математиков всех времён, «королём математиков». Лауреат медали Копли (1838), иностранный член Шведской (1821) и Российской (1824) Академий наук, английского Королевского общества .
С именем Гаусса связаны фундаментальные исследования почти во всех основных областях математики: в алгебре , теории чисел , дифференциальной и неевклидовой геометрии , математическом анализе , теории функций комплексного переменного, теории вероятностей, а так же в аналитической и небесной механике, астрономии, физике и геодезии. «В каждой области глубина проникновения в материал, смелость мысли и значительность результата были поражающими. Гаусса называли „королём математиков»
Определение. Системой m линейных уравнений с n неизвестными называется система вида
где a ij и b i ( i =1,…, m ; b =1,…, n ) – некоторые известные числа, а x 1 ,…,x n – неизвестные. В обозначении коэффициентов a ij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы .
Числа, стоящие в правых частях уравнений, b 1 . b m называются свободными членами.
Определение. Совокупность n чисел c 1 . c n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c 1 . c n вместо соответствующих неизвестных x 1 . x n .
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
Система может иметь единственное решение.
Система может иметь бесконечное множество решений. Например, . Решением этой системы является любая пара чисел, отличающихся знаком.
И третий случай, когда система вообще не имеет решения. Например, , если бы решение существовало, то x 1 + x 2 равнялось бы одновременно нулю и единице.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной . В противном случае, т.е. если система не имеет решений, то она называется несовместной .
Рассмотрим методы нахождения решений системы.
2.Численные методы решения уравнений
2.1 Метод подстановки
Этот метод мы применяли в 7-м классе для решения систем линейных уравнений. Тот алгоритм, который был выработан в 7-м классе, вполне пригоден для решения систем любых двух уравнений с двумя переменными х и у.
Алгоритм использования метода подстановки при решении системы двух уравнений с двумя переменными х, у.
1. Выразить у через х из одного уравнения системы.
2. Подставить полученное выражение вместо у в другое уравнение системы.
3. Решить полученное уравнение относительно х.
4. Подставить поочередно каждый из найденных на третьем шаге корней уравнения вместо х в выражение у через х, полученное на первом шаге.
5. Записать ответ в виде пар значений (х; у), которые были найдены соответственно на третьем и четвертом шаге.
Переменные х и у, разумеется, равноправны, поэтому с таким же успехом мы можем на первом шаге алгоритма выразить не у через х, а х через у из одного уравнения. Обычно выбирают то уравнение, которое представляется более простым, и выражают ту переменную из него, для которой эта процедура представляется более простой [1].
Пример 1. Решим систему уравнений
1) Выразим х через у из первого уравнения системы: х = 5 — 3у.
2)Подставим полученное выражение вместо х во второе уравнение системы: (5 -3у) у=2.
3)Решим полученное уравнение:
4) Подставим поочередно каждое из найденных значений у в формулу
Если то
5) Пары (2; 1) и решения заданной системы уравнений.
2.2 Метод алгебраического сложения
Этот метод, как и метод подстановки, знаком вам из курса алгебры 7-го класса, где он применялся для решения систем линейных уравнений. Суть метода рассмотрим на следующем примере.
Пример 2. Решим систему уравнений
Умножим все члены первого уравнения системы на 3, а второе уравнение оставим без изменения:
Вычтем второе уравнение системы из ее первого уравнения:
В результате алгебраического сложения двух уравнений исходной системы получилось уравнение, более простое, чем первое и второе уравнения заданной системы. Этим более простым уравнением мы имеем право заменить любое уравнение заданной системы, например второе. Тогда заданная система уравнений заменится более простой системой:
Эту систему можно решить методом подстановки. Из второго уравнения находим . Подставив это выражение вместо у в первое уравнение системы, получим
Осталось подставить найденные значения х в формулу .
Таким образом, мы нашли два решения системы:
2.3 Метод введения новых переменных
С методом введения новой переменной при решении рациональных уравнений с одной переменной вы познакомились в курсе алгебры 8-го класса. Суть этого метода при решении систем уравнений та же самая, но с технической точки зрения имеются некоторые особенности, которые мы и обсудим в следующих примерах [2].
Пример 3. Решим систему уравнений
Введем новую переменную . Тогда первое уравнение системы можно будет переписать в более простом виде: Решим это уравнение относительно переменной t:
Оба эти значения удовлетворяют условию , a потому являются корнями рационального уравнения с переменной t. Но значит, либо
, откуда находим, что х = 2у, либо ,
Таким образом, с помощью метода введения новой переменной нам удалось как бы «расслоить» первое уравнение системы, достаточно сложное по виду, на два более простых уравнения:
Далее каждое из двух полученных простых уравнений нужно поочередно рассмотреть в системе с уравнением х 2 — у 2 = 3, о котором мы пока не вспоминали. Иными словами, задача сводится к решению двух систем уравнений:
Надо найти решения первой системы, второй системы и все полученные пары значений включить в ответ. Решим первую систему уравнений:
Воспользуемся методом подстановки, тем более что здесь для него все готово: подставим выражение 2 у вместо х во второе уравнение системы. Получим:
Так как х = 2у, то находим соответственно х 1 = 2, х 2 = 2. Тем самым получены два решения заданной системы: (2; 1) и (-2; -1).
Решим вторую систему уравнений:
Снова воспользуемся методом подстановки: подставим выражение 2х вместо у во второе уравнение системы. Получим:
Это уравнение не имеет корней, значит, и система уравнений не имеет решений. Таким образом, в ответ надо включить только решения первой системы.
Метод введения новых переменных при решении систем двух уравнений с двумя переменными применяется в двух вариантах. Первый вариант: вводится одна новая переменная и используется только в одном уравнении системы. Именно так обстояло дело в примере 3.Второй вариант: вводятся две новые переменные и используются одновременно в обоих уравнениях системы. Так будет обстоять дело в примере 4.
Пример 4 . Решим систему уравнений
Введем две новые переменные:
Учтем, что тогда
Это позволит переписать заданную систему в значительно более простом виде, но относительно новых переменных а и b:
Применим для решения этой системы метод алгебраического сложения:
Так как а = 1, то из уравнения а + 6 = 2 находим: 1 + 6 = 2; 6=1. Таким образом, относительно переменных а и b мы получили одно решение:
Возвращаясь к переменным х и у, получаем систему уравнений, т.е.
Применим для решения этой системы метод алгебраического сложения:
Так как то из уравнения 2x + y = 3 находим:
Таким образом, относительно переменных х и у мы получили одно решение:
Метод разложения на множители.
Метод разложения на множители алгебраических систем двух уравнений с двумя неизвестными заключается в следующем. Если в алгебраической системе
то всякое решение системы уравнений
является решением совокупности систем
Пример 1. Решим систему
Заметим, что множитель так как в этом случае правая часть второго уравнения системы также обратилась бы в нуль. Следовательно, система (*) равносильна системе
Решим второе уравнение:
Выразив x из первого уравнения и подставив во второе, получили уравнения для нахождения y . В первое уравнение системы вместо y подставляем найденное значение и находим значения x
Теперь рассмотрим методы решения систем уравнений.
Метод исключения одной из неизвестных.
Метод исключения неизвестных позволяет последовательно сводить решение данной системы к решению системы (или совокупности систем), содержащей на одну переменную меньше. Этот метод последовательного исключения основан на очевидном утверждении, что система уравнений
равносильна системе уравнений
и аналогично для большего числа переменных.
Пример 2 . Решим систему
Левые части уравнений системы содержат одни и те же комбинации неизвестных. Умножим уравнения на подходящие множители с тем, чтобы исключить из системы одно из неизвестных. Из системы исключим 
Решим данное уравнение путем замены.
Пусть xy = t , тогда ,
Таким образом, исходная система распадается на системы:
В первом случае находим x 2 =1. Если x=1 то y=2 , а если x=-1 , то y=-2 .
Во втором случае, исключая , получаем x 2 =-209 . Поэтому вторая из двух последних систем не имеем действительных решений.
Метод алгебраических преобразований уравнений системы.
Уравнения системы можно складывать, вычитать, умножать на число, перемножать, делить, соблюдая при этом возможность выполнения таких операций. Заметим, что следствие системы, получаемое в результате алгебраических преобразований, содержит все решения исходной системы, и, кроме того, оно может содержать лишние корни.
1) если следствие не имеет решений, то и исходная система не имеет решений;
2) если решениями следствия окажутся действительными числа, то их нужно подставить в исходную систему и проверить, являются ли они ее корнями;
3) если решениями следствиями окажутся алгебраические выражения, то их нужно рассматривать совместно с уравнениями исходной системы. В этом случае получим равносильную систему или совокупность систем [3].
Пример 3. Решим систему
2.4 Метод замены переменных
Метод замены неизвестных основан на следующем утверждении.
Пусть дана система уравнений
и пусть система
имеет k различных решений
Тогда система (7) равносильна совокупности k систем
Пример 4 . Решим систему
Произведем замену. Пусть . Тогда
Складывая уравнения, получим
Преобразуем первое уравнение:
2.5 Системы однородных уравнений
Определение : Система двух уравнений с двумя переменными вида
называется однородной (левые части обоих уравнений однородные многочлены степени n от двух переменных).
Однородные системы решаются комбинацией двух методов: линейного преобразования и введения новых переменных.
Пример 5. Решим систему
Решение . Первое уравнение системы однородное (напомним, что уравнение вида f(x,y)=0 где f(x,y) — однородный многочлен — называется однородным уравнением). Заметим, что если положить y=0 то из однородного уравнения 3x 2 +xy-2y 2 =0 находим x=0. Но пара чисел (0;0) не удовлетворяет второму уравнению системы, поэтому y≠0 и, следовательно, обе части однородного уравнения 3x 2 +xy-2y 2 =0 можно разделить на y 2 (это не приведёт к потере корней).
Получим и , откуда находим, что или , т.е. x= — y или .
Типичные ошибки при решении систем и методы их устранения.
При решении некоторых систем иногда происходит потеря корней в ответе или появляются посторонние корни. Основная причина этого заключается в том, что осуществляются правдоподобные рассуждения, но теряется контроль над равносильностью переходов от одной системы к другой. Для того чтобы избежать подобных ошибок, нужно знать природу их появления и на определенном этапе решения произвести необходимые преобразования, проверку решения и т.д.
В качестве таких примеров рассмотрим решение нескольких систем нелинейных уравнений.
Пример 1. Решим систему уравнений
Неправильное решение . Вычтем из первого уравнения системы второе уравнение. Получим откуда x =11.
В этом случае корень уравнения, полученный после эквивалентного преобразования (вычли второе уравнение из первого), не проверили. Чтобы избежать подобной ошибки, необходимо после вычитания одного уравнения из другого решать систему уравнений, в которой обязательным является наличие уравнения, полученное после вычитания и одного из первоначальных уравнений.
Выполним эквивалентные преобразования:
Таким образом, при решении системы уравнений, необходимо записать такое же количество уравнений, которое было в условии, чтобы не получить посторонний корень.
Правильный ответ: 
Пример 2 . Решим систему уравнений
Решение . Выполним тождественное преобразование: разделим первое уравнение системы на второе уравнение, получим:
Решая систему методом подстановки, получим множество решений: <(3;0); (0;3)>.
Система (13) получена из системы (12) делением на число, отличное от нуля, поэтому системы (12) и (13) эквивалентны.
При решении систем нелинейных уравнений необходимо помнить о том, что такое тождественное преобразование как деление одного уравнения на другое не всегда приведет к правильному решению, так как может произойти потеря корня. Покажем это на следующем примере.
Пример 3 . Решим систему уравнений
Решение . Выполним тождественное преобразование: разделим первое уравнение системы на второе уравнение, получим:
Но в этом случае произошла потеря решения <(2;0)>. Это произошло потому, что при делении не было наложено условие 

Значит, метод деления одного уравнения на другое не безупречен, т.е.
к системе
можем потерять решения.
2.6 Матричный метод
Основные понятия при работе с матричным методом.
Определение. Матрица – это система элементов (функций, чисел и др. величин), которые расположены в виде прямоугольной таблицы. Общий вид записи матрицы представлен ниже:
Произвольный элемент матрицы обозначается через a ij (элемент i -й строки и j -го столбца). Тем, кто знаком с основами алгоритмизации и программирования, будет проще, если сравнить матрицу с двумерным массивом данных (в частном случае с одномерным массивом). Матрица имеет размерность, определяемую количеством строк и столбцов.
Основными действиями над матрицами являются:
сравнение (для матриц одинаковой размерности):
сложение и вычитание (для матриц одинаковой размерности):
умножение (количество столбцов первой матрицы равно количеству строк второй матрицы):
http://pandia.ru/text/78/153/54046.php
http://infourok.ru/tochnie-i-priblizhennie-metodi-resheniya-sistem-uravneniy-3823393.html